基于用户需求响应的综合能源交易机制研究

张 炜，杨 芸

（1.国网陕西省电力有限公司 调控中心，西安 710048；2.国网陕西省电力有限公司超高压公司，西安 710075）

0 引言

随着全球范围内对能源危机认识的不断深入，人类不断增长的能源需求与自然环境有限的供给之间的矛盾日益增加，如何高效灵活地使用能源成为亟待解决的问题。在能源需求种类不断增多、大规模可再生能源消纳问题日益凸显的背景下，打破现有各类能源系统独立运行的传统模式，实现多能源协同规划、共同运行是未来能源系统发展的必然趋势［1］。以天然气和电等一次、二次能源相结合的分布式综合能源站可以解决用户的电能、热能、氢能等多能源需求，因其高效、灵活、环保等多方面的优点，使其成为了近年来的研究热点［2］。

在综合能源系统及分布式能源站的研究方面，文献［3］采用场景分析对综合能源系统中的各个分布式能源站的出力进行了优化建模。文献［4］考虑能源转换运行成本，构建多目标优化模型，解决综合能源系统的优化调度问题。文献［5］基于分时电价，采用混合整数规划方法对包含多个分布式能源站的微网调度问题进行了研究。这些文献对综合能源系统的整体优化运行问题进行了研究，但是未对场环境下系统成员的市场行为进行讨论。

随着能源交易市场的不断发展和完善，在市场模式下多能源系统成员考虑如何制定合适能源生产策略和采购策略来实现自身利益的最大化，是研究的热点问题。当市场的参与者可以被认为是理性的时候，参与者之间相互影响的策略制定过程可以通过博弈论方法来描述和求解［6］。

在市场交易的博弈方面，现有研究主要包含两类。第一类是针对电能交易售电方和购电方之间博弈问题的研究。文献［7］—文献［10］利用Stackeberg 模型来构建多对多的交易方式，分析多个能源销售者和多个能源用户之间的均衡交易策略。文献［11］、文献［12］研究双方或者是多个微网之间的均衡博弈策略。第二类是针对售电方或者购电方单一群体内多参与者之间的博弈策略问题［13—18］。根据不同的市场特点，构建非合作或者合作博弈模型，寻找参与者的均衡策略。这两类研究主要都集中在购、售双方间或者购、售群体内的单一博弈问题，而且主要集中于电能交易，对于多能源系统能源间的耦合问题的博弈还鲜有研究。

本文将针对电能、热能和氢能的分布式综合能源系统交易机制及策略进行重点研究。该市场模式中包含提供能源的综合能源服务商和具有灵活需求响应能力的用户体。本文建立了双层博弈模型来解决综合能源服务商和用户间的均衡策略博弈问题和多用户间的相互竞争博弈问题。通过双层博弈模型寻找综合能源服务商与用户间的最优均衡博弈策略。为了求解该模型的均衡解，本文建立了分布式求解算法以降低模型计算的复杂性和保护市场参与者的隐私性。

1 市场结构

本文研究的分布式综合能源市场包含两类市场主体：综合能源服务商和用户体。系统中综合能源服务商的集合为M={1,2,…,m} ，用户的集合为N={1,2,…,n} 。其中综合能源服务商在批发市场中采购电和天然气，通过自身的能源转换设备为用户提供电能、热能和氢能。用户体（后文简称用户）为区域内能源用户的集合体，例如片区的居民用户或者是小型工业园区的负荷。用户的负荷包含各类电器及用电设备、取暖设备和氢能汽车，因而其能源需求为电能、热能和氢能。用户的负荷中包含一定比例的灵活负荷，每个用户根据其效用函数来调整负荷量，以达到能源消费的最大满意度。市场交易模式为多对多交易，参与交易的多个用户里每一个用户都可以选择多个综合能源服务商进行交易，每个综合能源服务商独立报价。

2 参与者效用函数

本节讨论综合能源市场交易的两类市场参与者（综合能源服务商和用户）的效用函数模型。参与者可以根据其效用函数模型形成能源交易价格和交易量。

2.1 综合能源服务商效用函数

综合能源服务商采购电和天然气，并以此为原料通过各类生产设备产出电能、热能和氢能来满足用户需求。其中，综合能源服务商将采购的电能通过变压器向用户直接提供电能，通过热泵向用户提供热能，通过电解槽向用户提供氢能；采购的天然气通过热电联产（combined heat and power，CHP）机组产生热能和电能，通过燃气锅炉产生热能。综合能源服务商的能源转换结构如图1 所示，能源转换方程为

图1 综合能源服务商能源转换结构图Fig.1 Structural chart of energy conversion for integrated energy service providers

式中：O、O、O分别为综合能源服务商i在时刻t生产的电能、热能和氢能；E、E、E、E分别为综合能源服务商i在时刻t的变压器、电解槽、电热泵的耗电量、总耗电量；、、分别为综合能源服务商i在时刻t的CHP 机组、燃气锅炉耗气量、总耗气量；ηT、η、η、ηHP、ηGB、ηS分别为变压器、CHP 机组产电、CHP 机组产热、电热泵、燃气锅炉、电解槽的能源转换效率。式（1）为生产电能、热能和氢能的能源转换方程，式（4）、式（5）表示各类能源转换设备应符合设备的生产能力。

市场交易中，综合能源服务商在批发市场采购电能和天然气，通过能源转换设备向用户供给各类能源。每个综合能源服务商在交易时需要制定所交易能源的出售价格，并对能源转换过程进行优化来将其收益最大化。综合能源服务商的效用函数可以用能源销售的利润来表述，其优化问题具体描述为

式中：p、p、p分别为综合能源服务商i公布的时刻t的电能、热能、氢能出售价格；d、d、d分别为用户j在时刻t的电能、热能、氢能需求量；αe、αr、αh分别为电能、热能、氢能在传输过程中的网损系数；(E)为综合能源服务商在批发市场采购的电能和天然气的成本。

2.2 用户效用函数

效用函数在微观经济学中一般用来量化地表示消费者从消费既定商品中所获得的满足程度。用户对不同的价格会有不同的消费需求，其消费行为可以用不同特点的效用函数来表示。对于能源方面的消费，通常采用二次函数来对用户的个人偏好以及其消费能源所带来的满意度进行建模。本文定义用户的综合效用函数为各类能源消费满意度的和，具体表述为

式中：w、w、w、a、a和a为用户j的效用函数参数，其中w、w和w为变化参数，将随着用户不同而各不相同，用来描述不同用户消费特性及满意度的差异；a、a和a为固定参数。

对于多对多模式下的综合能源交易，当m个综合能源服务商发布时刻t的能源价格p、p、p后，每个用户将根据价格决定购买的能源量，以消费者剩余最大化为目标。用户购买能源的消费者剩余在这里即能源使用的满意度（效用函数）与能源购买的成本之间的差值，则用户在能源消费时最优需求响应问题可以表述为

由式（14）、式（15）可见，用户的需求响应通过最大化消费者剩余体现。在综合能源服务商公布各类能源价格后，用户将根据能源价格调整各类能源的购买量以实现消费者剩余最大化。对于不同的能源类型，用户效用函数的参数是不同的，因此在需求响应时，对价格的响应程度也各不相同，体现了用户对不同能源响应的差异性。

3 参与者博弈行为分析

在综合能源市场交易中，参与交易的双方拥有不同的利益诉求。从第2节的分析可知，综合能源服务商的主要目标是以尽可能高的价格销售尽量多的能源以获得更多的利益（式（6））。而用户的主要目标是以尽可能低的价格购买尽量多的能源以获得更多的消费者剩余（式（14））。因此需要采取合适的策略来维持综合能源服务商和用户之间的平衡。

由于市场交易的参与者在制定策略时，会受到其他参与者行为的影响，各参与者之间的关系如图2所示。从图2 中可以看出，市场交易存在着双层博弈。上层博弈是综合能源服务商之间的博弈。不同服务商通过竞争把能源销售给用户。每一个服务商都需要选择采购合适的能源原料和转换比例并制定合适的出售价格以达到其效益最大化。下层博弈是用户之间的博弈，用户需要通过相互博弈决定在不同综合能源服务商购买能源的比例。根据博弈论的理论，综合能源服务商之间的博弈是一种非合作竞争博弈，而用户间的博弈是一种能源消费的演化过程，可以运用演化博弈的理论进行建模。

图2 市场参与者博弈关系Fig.2 Game relations among market participants

3.1 用户间演化博弈

在包含多个能源销售方和多个能源购买方的市场交易问题中，当认为具有理性的用户之间进行消费竞争时，用户之间就采购能源的综合能源服务商选择问题构成演化博弈。建立合适的演化复制因子，可以寻找到演化博弈的均衡解。

3.1.1 种群行为和动态复制

根据消费者剩余函数式（14），用户从综合能源服务商i处购买能源，则其福利可以表示为

式中：d、d分别为用户j在时刻t可以从综合能源服务商i处购买的能源的最小值和最大值，其值应该在式（15）中用户需求的最小、最大值的范围内。

根据式（16），则用户j在时刻t可以从综合能源服务商i处购买的最优能源量（此处以电能示例，热能和氢能的最优表达式类同）为

如此，在时刻t用户从综合能源服务商i处购买的能源总量为

根据这一结果，可以计算综合能源服务商的能源购售比

式中：为由采购的能源原料量（E）根据能源转

在此基础上，用户从综合能源服务商i处购买能源获得的总效用值为

根据用户总效用值，设计种群动态选择行为

3.1.2 演化均衡

用户在演化博弈过程中，当种群不再改变其选择策略时，可以认为是达到演化均衡的状态。根据种群演化行为的式（21）可知，演化过程中种群的选择策略是由不同综合能源服务商产生的用户总效用π与平均效用的差值所决定，因此当各个效用值与平均效用相等时，即达到演化平衡

动态复制可以用离散的复制因子通过迭代的方式来逼近。离散的复制可以通过以下迭代方式来实现

3.2 综合能源服务商之间的非合作博弈

在市场交易过程中，每一个综合能源服务商都将制定自己的能源销售价格和销售量，由于市场为多对多交易模式，用户可以自由选择不同的服务商采购能源，因为不同服务商之间存在非合作的竞争关系。因此，本文采用非合作博弈模型来模拟销售端综合能源服务商之间的竞争。

3.3 Stackelberg主从博弈

在综合能源交易中，综合能源服务商和用户作为交易的双方同样存在博弈行为。本文构建Stackelberg 主从博弈模型来描述二者之间的关系。综合能源服务商作为领导者，其目标是通过制定合适的能源销售价格来获得最大的能源销售收益。用户作为追随者，其目标是根据服务商公布的能源价格制定最优策略使消费者剩余最大化。

传统的集中式算法需要知悉交易各方目标函数参数的各项信息，但在实际交易中，各交易者存在市场竞争的关系，详细的交易信息一般难以准确获取。为了保护市场交易参与者的隐私性，同时降低计算的复杂性，本文设计了一种分布式算法来寻找主从博弈的Stackelberg 均衡解。在Stackelberg 主从博弈模型中，综合能源服务商与用户之间通过能源价格实现博弈。价格的变化一方面会影响综合能源服务商的供能策略，另一方面会影响用户的用能策略。因此应当通过分布式算法寻找博弈双方的价格平衡点，也即博弈的均衡解。

在交易开始时，市场运营者首先生成初步的能源价格，并发布给综合能源服务商和用户。综合能源服务商根据该价格求得优化的能源转换优化量，用户根据该价格求解其最优能源需求量，双方将能源量信息反馈给市场运营者。市场运营者根据最新的能源供给量和需求量来更新能源价格，随后进入下一次迭代。价格的更新策略如下

根据收敛条件判断是否结束迭代，迭代收敛判定如下

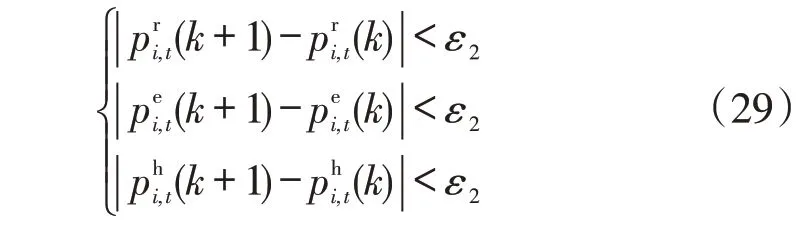
当满足迭代条件即综合能源服务商的供应量和用户的需求量达到平衡时，便可以得到能源价格的稳定解。分布式算法流程图如图3所示。

图3 分布式算法流程图Fig.3 Flow chart of distributed algorithm

4 算例分析

本文以24 h 的算例仿真分析来验证所提出的综合能源系统双层博弈模型的有效性以及求解博弈均衡的分布式算法的收敛性。

4.1 市场交易参数

综合能源系统中包含两个综合能源服务商，每个综合能源服务商均供应电能、热能和氢能。综合能源服务商在日前市场采购电能和天然气，通过变压器、热泵、电解槽、CHP机组和燃气锅炉等不同能源相互转化的设备为用户提供电能、热能和氢能。各类设备的转化效率如表1所示。

表1 设备转化率参数Table 1 Device conversion rate parameters

综合能源系统中包含5 个用户体，每个用户体约由50 个用户构成，这些用户共拥有10 辆氢能汽车。负荷区内用户拥有电力负荷、热力负荷和氢能汽车，因而需要从综合能源系统购买电能、热能和氢能。为便于统一计算和对比分析，将用户的热能负荷和氢能负荷的单位统一换算为kW，其中热值单位1 MBtu（英热单位）相当于293.2 kWh［20］；氢能按照电解产生1 kg H2需耗费38 kWh 电能计算。用户电能负荷曲线参照文献［21］，氢能负荷按照用户每日需加氢1.5 kg计算。具体负荷数据如图4所示。

图4 用户各类能源平均负荷Fig.4 Average energy load of all types of energy

4.2 市场交易结果分析

算例中包含两个综合能源服务商，因为每个综合能源服务商能源转化参数以及在批发市场的能源采购量都各不相同，因而用户在选择时的侧重将存在差异。根据前文所述，用户在每一时刻的市场交易中都会根据演化博弈模型寻找在两个综合能源服务商购买能源的最优分配比例。图5展示了在20:00用户对电能、热能和氢能3类不同能源在两个综合能源服务商的采购分配比例。对于电能负荷，67.83%从服务商1购买，32.17%从服务商2购买；对于热能负荷，从服务商1处购买的比例为36.40%，从服务商2处购买的比例为63.60%；对于氢能负荷，从服务商1 处购买的比例为53.58%，从服务商2 处购买的比例为46.42%。从两个综合能源服务商的能源转换效率参数可知，服务商2 的热转换效率高于服务商1，因而用户热负荷选择服务商2 的比例较大。同理，服务商的电转换效率和氢转换效率参数的差异同样对用户的电负荷和氢负荷选择产生相同的影响。

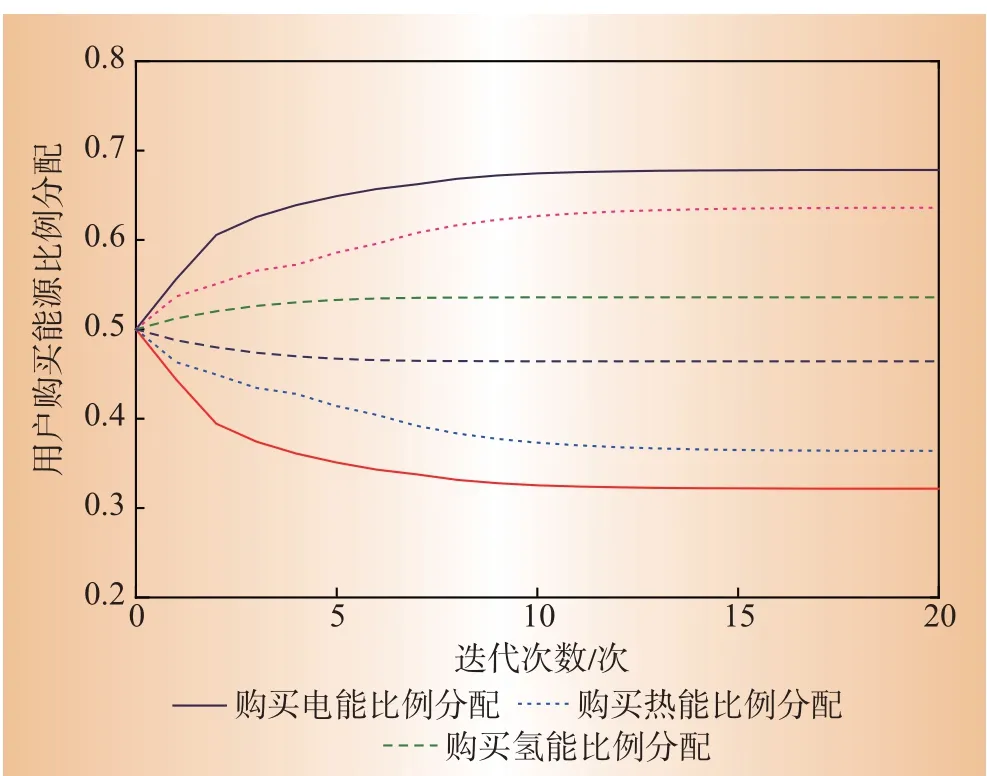
图5 用户在不同综合能源服务商处购买能源比例Fig.5 Proportion of users purchasing energy at different integrated energy service providers

市场交易的电价格、热价格和氢价格如图6 所示。从图中价格曲线可以看出各类负荷的价格波动总体趋势与该类负荷的变化趋势基本相同。

图6 能源价格对比Fig.6 Energy price comparison

综合能源服务商供应的3种能源之间存在耦合关系，因而各类能源的价格也存在一定的关联。可以看出在20:00—21:00 时段，各类负荷都具有较高的负荷值，其中电负荷为一天中的负荷峰值，因此这一时间段用户的整体能源需求为全天最高，各类能源的价格也高于其他时段相同负荷需求时刻的价格。例如，热负荷在20:00 的负荷需求小于2:00时的负荷需求，但是其热价格却高于2:00时的热价格。可以看出，综合能源系统的能源价格不仅仅由其单一能源的供需情况决定，还由存在耦合关系的多种能源共同决定，价格的形成更加复杂。

为了验证算法的博弈均衡，图7给出了20:00的各类能源价格迭代收敛过程。从图中可以看出能源价格在35次以内便可以收敛，验证了所提分布式算法可以快速找到博弈的均衡解。在迭代过程中各类能源的收敛次数各不相同，这是因为在迭代计算时，各类能源的价格计算相互独立，因而不同效用参数以及供需情况的差异会导致价格的收敛速度不同。

图7 交易价格迭代曲线Fig.7 Transaction price iteration curves

各个用户和综合能源服务商的效用值如表2所示。表中对3种不同交易机制下各市场主体的效用值进行了对比分析。其中“无DR方法”为在本文提出的方法中不考虑负荷量根据电价变动的灵活可调整性，“直接交易”为传统方式下用户按照固定价格直接从系统购买能源。从表中可以看出本章所提出的综合能源市场交易方式与传统用户直接参与系统交易的方式相比，用户的效用值有较大的提高。这是因为灵活的市场机制，通过Stacklberg主从博弈方法求得的市场交易结果能够满足用户的策略需求，使得用户在交易过程中作为博弈的参与方影响价格的确定，这与传统模式中用户直接从大系统按照固定价格采购能源的方式相比，能源价格的确定更加公平和准确。

同时，在本文所提出的综合能源框架下是否考虑负荷灵活性会产生不同的结果，通过对比可以发现计及需求响应的交易方式，用户的效用值呈上升趋势，而综合能源服务商的效用值呈下降趋势，这是因为用户会根据市场价格的高低灵活地调整负荷，减少购买能源的费用以获得更高的效用。但作为博弈的另一方，综合能源服务商的效益会有所减少，但通过表2 的数据可以看出整个系统的整体社会效益会有所增加。

表2 不同方法效用值对比Table 2 Comparison of utility values of different methods

5 结束语

本文针对多能源协同规划、共同运行的能源系统发展趋势，提出了包含电能、热能和氢能的综合能源市场交易机制，以促进综合能源系统的发展。本文所提出的市场模式中包含提供能源的综合能源服务商和具有灵活需求响应能力的用户。为解决综合能源服务商和用户间的均衡策略博弈问题和多用户间的相互竞争博弈问题，建立了双层博弈模型，上层为综合能源服务商之间的对能源销售价格非合作博弈，下层为多用户之间的演化博弈模型。同时，根据综合能源服务商与用户间的交易次序，构建了二者之间的Stackelberg 主从博弈模型。通过双层博弈模型寻找综合能源服务商与用户间的最优均衡博弈策略。

算例仿真进一步证明了综合能源交易市场的有效性，仿真结果也验证了分布式综合能源交易市场机制不仅可以使市场交易在多能源之间得到耦合，提高能源使用效率，还可以促进用户的灵活响应，降低负荷峰值以提升用户效益。

考虑到机组特性及电网运行情况会对市场交易产生影响，本文后续将针对这一类问题继续开展相关研究。D