满足电网调峰的化学储能最优容量敏感因素分析

朱刘柱，叶 斌，任曦骏，王 宝，任 可，陶文斌

（1.国网安徽省电力有限公司 经济技术研究院，合肥 230022；2.国网江苏省电力有限公司

徐州供电分公司，江苏 徐州 221005；3.华北电力大学 现代电力研究院，北京 102206）

0 引言

近年来，风电、光伏等新能源发电给电网运行带来了诸多挑战，其中调峰问题尤为凸显［1—2］。

为了缓解电网调峰压力，能够实现电能时移的储能设施进入了专家学者的研究范畴［3］。化学储能具有使用方便、环境污染少、不受地域限制、在能量转换上不受卡诺循环限制、转化效率高、比能量和比功率高等优点［4—5］，近年来发展尤为迅猛。国内外多个大容量化学储能电站参与电网调峰的工程已投入实际应用［6—8］。

目前化学储能成本仍然较为昂贵，因此需要合理配置化学储能的容量。之前的学者对用于电网调峰的化学储能容量配置问题已有一些研究［9—15］。文献［9］分析了风电大规模接入对系统峰谷差的影响机理，提出了一种用于松弛调峰瓶颈的储能系统容量配置方法；文献［10］提出了采用化学储能参与系统调峰的充放电策略，并基于所提出的策略建立储能电站选址定容模型；文献［11］在储能容量规划模型中引入了电池可变寿命模型；文献［12］、文献［13］建立了储能容量配置的双层优化模型；文献［14］利用蒙特卡洛模拟方法生成风电出力场景，然后采用围绕中心点划分（partitioning around medoid，PAM）算法聚类削减场景；文献［15］分别对集中式与分布式接入方式的各类储能系统的规划方法和求解算法进行了综述。

上述研究一方面多聚焦于化学储能容量的优化配置，而忽略了对影响化学储能容量配置结果的敏感因素的分析研究；另一方面在计算方法上多是采用典型场景法，无法真实模拟电力系统的生产过程，并且典型场景法通常利用聚类算法选取典型场景来进行研究，不同的聚类算法得到的典型场景可能不同，场景选取存在不确定性，因而导致最终结果缺乏说服力。本文首先构建了一种用于电网调峰的化学储能最优容量配置模型，通过对各储能容量待选方案进行全年全时段生产模拟得到储能的最优配置方案；然后，在所建立的优化模型基础上，归纳了影响储能容量配置的敏感因素，并对敏感因素的影响方式和影响程度进行了定量计算和逻辑分析。

1 储能容量配置优化模型

1.1 目标函数

本文以目标规划年各类电源、负荷的规划或预测数据为边界，以系统总成本最小为目标构建函数，研究化学储能的最优配置容量。具体的目标函数表达式为

式中：M为发电机组总数；Ci(t)为发电机组i在t时刻的发电成本；SUi(t)为发电机组i在t时刻的启动成本；Cls为切负荷损失；Ccur为弃电损失；Cess为储能年投资成本。其中，发电成本、启动成本、切负荷损失、弃电损失之和为系统运行成本。

考虑到目前我国大部分省份仍以火电机组为主要调峰电源，以下发电成本模型以火电为代表进行描述，其他类型电源发电成本模型可同理构建。

（1）火力发电成本

式中：Pi(t)为火电机组i在t时刻的出力；ai、bi和ci均为火电机组i的成本系数；kcoal为标准煤价格。

（2）火电启动成本

式中：csu,i为火电机组i的启动费用；ui(t)为火电机组i在t时刻的启动状态，ui(t)=1表示火电机组i在t时刻正在启动。

（3）切负荷损失

式中：kls为单位切负荷损失；Pls(t)为t时刻切负荷的功率。

（4）弃电损失

式中：kcur为单位弃电损失；ΔPcur(t)为t时刻弃风、弃光、弃水的总功率。

（5）化学储能年投资成本

式中：ce为化学储能系统单位投资成本；Eess,max为化学储能的额定容量；i为折现率；N为化学储能运行年限。

1.2 约束条件

（1）火电运行状态约束

式中：vi(t) 为火电机组i在t时刻的停机状态；vi(t)=1 表示火电机组i在t时刻正在停机；oi(t)为火电机组i在t时刻的运行状态，oi(t)=1 表示火电机组i在t时刻正处于运行状态。

（2）化学储能电站运行约束

式中：Pess,c(t)和Pess,d(t)分别为化学储能电站在t时刻的充电功率和放电功率；Pess,max为化学储能的最大充电和放电功率；Eess(t)为化学储能在t时刻存储的电量；SOCmax和SOCmin分别为化学储能荷电状态的上限和下限；μm,c和μm,d分别为化学储能的充电效率和放电效率。

此外，还有系统功率平衡约束、火电出力约束、火电机组爬坡率约束、火电最短运行和停机时间约束、火电备用约束、抽水蓄能电站运行约束。

1.3 模型求解

本文以1 h 为单位仿真系统全年8 760 h 运行。由于模型涉及机组多，仿真周期长，一次迭代运算耗时很长，所以本文首先采用枚举法得到多个储能容量方案（功率容量和电量容量之比按1：2配置［7］，电量容量步长取200 MWh），然后依次优化计算不同储能容量下系统的最优运行成本，再叠加该方案的储能年投资成本，得到系统的总成本，最后比较所有方案，优选出总成本最低的方案。

权衡仿真时间与精度，本文以96 h 为一个仿真周期，具体思路为：每次仿真96 h机组组合，输出结果仅读取前72 个h，然后以第72 h 的测算结果作为初值仿真测算后96 h，以此类推，滚动测算。

具体求解方法为：首先将机组组合模型线性化，然后利用GAMS软件中的CPLEX求解器求解。

2 敏感因素

基于本文所建立的优化模型，可以将影响化学储能最优配置容量的敏感因素归纳为客观需求因素和储能自身因素两大类。

2.1 储能因素

（1）单位投资成本

化学储能技术类型众多，常见的有锂电池、铅碳电池、液流电池。由于原材料成本和技术成熟度等因素限制，不同类型电池的单位投资成本各异，成本下降潜力也各有不同。

（2）储能运行年限

储能运行年限与储能的技术类型以及运行方式有关。比如每日以额定功率一充一放的储能系统，钠硫电池的运行年限是阀控铅酸电池的3倍，而每日两充两放的储能系统的运行年限则会低于每日一充一放的储能系统。

上述这2个因素将会影响到优化模型中储能年投资成本的取值，从而影响储能的最优配置方案。

2.2 需求因素

（1）负荷尖峰需求

每年夏季高温时期，由于空调负荷增长等因素的影响，电力负荷会达到高峰。在不扩建其他类型电源的前提下，负荷尖峰需求的变化将影响模型中的火电机组的运行成本和切负荷成本，从而影响储能的最优配置方案。

（2）负荷低谷调峰

风电出力的反调峰特性以及光伏出力与高峰负荷的不匹配，使得电网净负荷峰谷差增大，尤其在夜间风电大发，用电负荷却处于低谷，此时火电负荷率下压空间枯竭，为了满足电力供需平衡，不得不限制风电出力。因此，负荷低谷调峰需求将影响模型中的火电机组的运行成本和弃电损失，从而影响储能的最优配置方案。

（3）火电节能降损

火电调峰可分为深度调峰和启停调峰，前者又可进一步分为常规调峰、稳燃不投油深度调峰和投油深度调峰，任何一种调峰都要带来额外的燃料或机组损耗。利用储能调峰可以减轻火电调峰压力，减少模型中火电的运行成本，进而影响储能的最优配置方案。

3 算例分析

3.1 仿真参数

本文以某地区电网目标规划年的规划统调电源和预测统调负荷数据为基础，全年最大负荷为44 320 MW。

3.2 最优容量分析

不同化学储能规模下的系统年运行成本和计入年储能成本后的年系统总成本如图1所示。从图1 中可以看出随着化学储能规模的增加，最初运行成本呈快速下降趋势，之后下降趋势趋缓。当化学储能容量为2 800 MWh时，系统总成本达到最小。

图1 成本变化趋势Fig.1 Cost variation trend

图2 更直观反映了每增加200 MWh 储能，运行成本减少量与化学储能投资成本增加量的对比。其中运行成本变化曲线表示每增加200 MWh 化学储能减少的运行成本，储能投资成本变化曲线表示每增加200 MWh化学储能增加的年投资成本，曲线上每个点所对应的横坐标表示每增加200 MWh 化学储能后储能的累计总容量。可以看出，由于储能单位成本固定，所以每增加200 MWh化学储能所增加的年投资成本也固定不变，而运行成本减少值则呈阶梯状下降趋势。2条曲线交点的纵坐标即为最优储能配置容量。

图2 成本变化量变化趋势Fig.2 Variation trend of variational cost

深入分析可以发现，运行成本减少的主要原因在于储能的投入减少了系统切负荷的损失。图3为每增加200 MWh储能能够减少的切负荷电量，可以发现它与图2中运行成本变化曲线的变化趋势基本一致。当储能容量较小时，增加储能容量能够缓解多时段的供需紧张矛盾，减少多个时段的切负荷量，所以此时增加储能容量可以减少较大的切负荷损失。而当储能容量增加到一定规模时，需要切负荷的时段将逐步减少，此时继续增加储能容量能够带来的切负荷量减少量也在逐步降低。

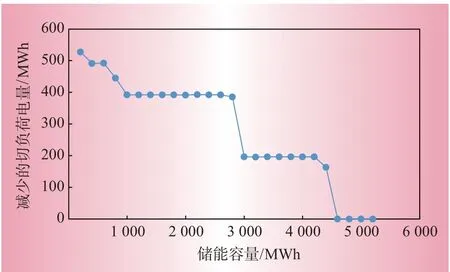
图3 切负荷电量减少量的变化趋势Fig.3 Electric quantity variation trend of reduced load shedding

当新增储能容量大于2 800 MWh 时，新增投资成本不能被因此降低的切负荷损失所弥补。

3.3 敏感因素对配置结果的影响

第2 节论述了储能容量配置的敏感因素，下面将通过算例实证其影响方式和影响程度。由于火电稳燃不投油深度调峰和投油深度调峰涉及机组损耗、投油损耗等多重因素较为复杂，所以本文在研究时只考虑了常规调峰。文献［16］指出抽水蓄能电站的节煤效应不足以支撑其投资运维成本，而化学储能相比抽水蓄能成本更高，因此需求因素中火电的节能降损对储能容量的影响不大，本文不再就此展开分析。

（1）储能因素

图4所示为不同化学储能单位投资成本下，不同规模的储能对应的系统总成本，可以看出同一规模储能，单位投资成本越高系统总成本也越高。当单位投资成本分别为1.6元∕Wh、1.2元∕Wh、0.8元∕Wh时，化学储能最优规模分别为2 800 MWh、4 200 MWh、4 400 MWh，所以储能单位成本降低可以促进最优容量增加，并且成本因素对储能容量需求的影响呈逐渐衰弱趋势。

图4 单位投资成本对最优容量的影响Fig.4 Impact of unit investment cost on optimal capacity

改变储能的运行年限，不同规模的储能对应的系统总成本如图5所示，当运行年限分别为6 a、10 a、14 a时，最优规模分别为1 200 MWh、2 800 MWh、3 600 MWh，所以储能运行年限增加也可以促进最优容量增加。

图5 运行年限对最优容量的影响Fig.5 Impact of operating years on optimal capacity

（2）需求因素

不同规模化学储能在不同单位切负荷损失时的系统总成本变化如图6 所示，不同单位切负荷损失时的最优化学储能规模如表1所示。从表1中可以看出当单位切负荷损失为30 元∕kWh 时，最优化学储能容量为0，此时新增储能不具有经济性；当单位切负荷损失为70 元∕kWh 时，最优化学储能容量为400 MWh，此时新增储能略具经济性。由此可见，储能的优化配置容量与单位切负荷损失正相关。文献［17］指出，小工业用户短时停电的单位失电损失可以达到近70元∕kWh，考虑到未来储能成本还会下降，所以为避免切负荷而配置储能存在一定的现实可行性。

图6 单位切负荷损失对最优容量的影响Fig.6 Impact of unit load shedding loss on optimal capacity

表1 不同单位切负荷损失下的最优储能容量Table 1 Optimal capacity under different unit load shedding loss

在基础场景中，由于风光渗透率较小，所以尽管单位弃电损失设为0，系统全年仍无弃风现象发生。扩大风电装机规模，研究单位弃风损失对储能配置结果影响，结果如图7所示，可以看出当单位弃风损失低于5元∕kWh 时，新增储能并不能带来系统总成本降低，此时新增化学储能并不具有经济性；当单位弃风损失达到10元∕kWh时，配置1 000 MWh储能将使系统总成本达到最小，所以单位弃风损失增加将促进对储能的需求。但是，现实中风电上网价格一般不会高于1 元∕kWh，所以不会出现很高的单位弃风损失，并且短期内化学储能的年投资成本也不会陡然大幅降低，所以单纯为避免弃风而配置储能尚缺乏经济性；但是当对弃风、弃光率的考核变得严苛时，对储能的需求将增加。

图7 单位弃电损失对最优容量的影响Fig.7 Impact of unit curbed output loss on optimal capacity

4 结束语

本文构建了用于调峰的化学储能容量配置模型，采用线性求解器对各储能容量待选方案进行全年全时段生产模拟，重点分析了影响储能最优容量的敏感性因素。结果表明，储能运行年限、单位切负荷损失、单位弃电损失与储能的最优容量正相关，单位投资成本与储能的最优容量负相关。单纯为避免弃风而配置储能尚缺乏经济性，但是为避免切负荷而配置储能却存在一定的现实可行性。由于本文仅考虑了火电的常规调峰，因此仅在单位切负荷损失和单位弃电损失极大时，新增化学储能才具备经济性。若要全面论证化学储能调峰的经济可行性，下一步还需考虑火电机组的稳燃不投油调峰和投油调峰。D