广义四元数群上正规弧传递凯莱图

甯鸿琳，潘江敏

(云南财经大学 统计与数学学院，云南 昆明 650221)

本文研究的图都是有限连通的无向图. 设Γ 为一个图，我们用VΓ，EΓ，AΓ 和 Aut(Γ) 分别表示它的顶点集、边集、弧集和全自同构群，称Γ 的顶点个数 |VΓ| 为 Γ 的阶数. 与顶点 α 相邻接的顶点组成的集合称为α的邻域，记为 Γ (α)， 称 |Γ(α)| 为 点 α 的度数，记为 val(α). 如果每个点的度数都相同，则称Γ 为正则图，此时图Γ 的度数 v al(Γ) 等于点 α 的度数. 设X≤Aut(Γ) 为图Γ 的一个自同构群，如果X在VΓ，EΓ 或AΓ 上传递，则分别称Γ 是X-点传递图、X-边传递图或X-弧传递图. 如果X分别地在VΓ，EΓ 上传递，但在AΓ 上不传递，则称Γ是X-半弧传递图.

给定一个群G和非空集合S⊆G＼{1} 使得S=S-1:={s-1|s∈S}，定义群G关于S的凯莱图Cay(G,S)如下：顶点集为群G中的所有元素，顶点g与h相邻接当且仅当hg-1∈S. 易知群G的右正则表示G^ 是图Cay(G,S) 的自同构. 容易验证每一个群自同构 α ∈Aut(G) 可以诱导图 C ay(G,S) 到图 C ay(G,Sα) 的同构[1].

群与图是组合数学的一个分支，主要内容是应用群的理论来研究图论问题及应用图的理论来研究群论问题[2-8]. 凯莱图是代数图论中最重要的图类之一，凯莱图的研究是代数图论的中心课题之一. 从研究来看，如果不赋予高对称的条件(比如2-弧传递性)，要分类一般群上弧传递凯莱图是极其困难的，学者们的研究主要是关于一些具体群类上的凯莱图[9-12]. 对于广义四元数群上的凯莱图，小度数的情形已经得到了一些好的结果，比如：4 倍素数幂阶广义四元数群上4 度凯莱图已被完全分类，4 倍素数幂阶广义四元数群上5 度连通无向凯莱图的CI 性、正规性和弧传递性已被很好地刻画[13-15]，对于度数大于等于6 的情形结果很少. 本文将对广义四元数群的正规弧传递凯莱图进行一般的研究.

本文所使用的术语和符号都是标准的. 对于一个正整数n，我们用 Z2n表示 2n阶循环群，用 Z*2n表示模 2n的剩余类关于剩余类乘法构成的群，用 Q4n表示 4n阶广义四元数群. 对于素数p和正整数r，我们用Zpr表示pr阶循环群. 对于群G，我们用 o(a) 表示G中元素a的阶. 对于2 个群N和H，我们用N×H表示N与H的直积，用N.H表示N被H的扩张，如果这个扩张是可裂的，则表示为N:H. 对于群X及其子群G，我们用 c oreX(G) 表示包含在G中X的最大正规子群.

1 预备知识

群G的全体自同构构成的群称为群G的全自同构群，记作 A ut(G) . 设群G在非空集合 Ω 上有一个作用 ψ，如果群G作用在 Ω 上的核为单位元群，则称作用 ψ 是忠实的，此时G可视为 Ω 上的置换群.

定义 1 设群G是非空集合 Ω 上的传递置换群，称G是 Ω 上的本原置换群，如果G作用在 Ω 上不存在非平凡的块；称G是 Ω 上的拟本原置换群，如果G的每一个非平凡正规子群作用在 Ω 上都传递.

易知本原置换群一定是拟本原置换群，反之则不成立. 根据O’Nan-Scott 定理，拟本原置换群可分为8 类. 特别地，如果拟本原置换群G可解，则称G为仿射型拟本原置换群. 仿射型拟本原置换群是本原置换群.

定义 2 称图Γ 为X-局部本原图，如果对任意 α ∈VΓ，点稳定子群

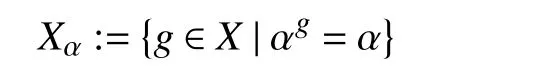
作用在邻域 Γ(α) 上都是本原的. 称图Γ 为X-局部拟本原图，如果对任意 α ∈VΓ， 点稳定子群Xα作用在邻域 Γ (α) 上都是拟本原的.

定义 3 设 Γ=Cay(G,S) 为X-弧传递凯莱图，X≤Aut(Γ)， 称Γ 为X-正规弧传递凯莱图，如果G^ ◁X. 特别地，称Γ 为群G上的正规凯莱图，如果G^ ◁Aut(Γ).

定义 4 设Γ 为X-点传递图，且X有一个在VΓ 上不传递的正规子群N. 定义Γ 的由N导出的正规商图(记为 ΓN)的顶点集为N在VΓ 上的所有轨道(记为VΓN)，且 ΓN的2 个顶点B,C∈VΓN邻接当且仅当B中的某个顶点与C中的某个顶点在Γ 中邻接. 特别地，称Γ 为 ΓN的正规覆盖，如果Γ 和 ΓN的度数相同；称Γ 为 ΓN的正规多重覆盖，如果B中的任意一点恰好与C中l个点相邻接(l与B，C的选择无关).

点传递且边传递图是其正规商图的正规多重覆盖[16]. 下面的命题是关于正规边传递凯莱图的一个重要性质.

(2) Γ 是 ΓN的正规多重覆盖， val(Γ)=k·val(ΓN) ，其中k=|S s∩N|，s∈S.

引理 2[18]设 Γ =Cay(G,S) 是X-正规局部本原凯莱图，其中G^

(1) 〈S〉=G，S中的每个元都是对合且在 A ut(G,S) 中共轭.

(2)X1≤Aut(G,S) 作用在S上忠实且本原.

2 主要结果

我们先证明以下4 个引理.

因为2-弧传递的凯莱图一定是局部本原的，而局部本原的凯莱图一定是局部拟本原的，故由定理3 可得以下推论.

推论 1 不存在广义四元数群上的X-正规2-弧传递或X-正规局部本原凯莱图.