基本不确定信息软集的得失优势度评分方法及其多属性决策

巩增泰，颜小燕

(西北师范大学 数学与统计学院，甘肃 兰州 730070)

Zadeh 于2011 年所提出的Z-数概念[1]，因同时考虑了不确定信息的模糊性和随机性，显式地加入了模糊约束的可靠性信息，使得对于不确定信息的描述更加接近人类的思维方式[2-3]. 对于Z-数所描述的不确定信息的模糊约束，2017 年，Mesiar 等[4-5]进行了改进，提出了基本不确定信息的概念和定义. 基本不确定信息由评估值(或观测值)和其确定度(可靠性)对不确定信息的模糊性和随机性进行了刻画，其特点是不仅以评估值(或观测值)评价对象的不确定描述，而且以确定度衡量信息描述的质量. 即确定度越高，对于评估值或观测值的确定程度越高，反之确定度越低，对于评估值或观测值的确定程度越低. 从而基本不确定信息的研究为涉及不确定性数据的建模提供了一个更加简单有效的方法. 由于软集理论从对象论域和参数空间2 方面描述对象的不确定性，已成为一种处理众多不确定性(包括随机性、模糊性、不完全性和不可区分性等)的统一数学模型[6-9]，并广泛应用于不确定性信息理论、决策分析、模式识别和数据挖掘等诸多领域. 2020 年，陶志富等[10]结合基本不确定信息和软集理论，提出基本确定信息软集的概念对软集进行了新的拓展，并提出了基于层次结构和近似元素聚合的决策方法. 基本不确定信息软集结合软集参数化的特征和基本不确定信息确定度的优点，克服了基本不确定信息参数化的不足，同时确定度能够提高信息评价的质量. 由吴兴利和廖虎昌2019 年所提出的得失优势度评分方法(GLDS)[11]，在多属性决策中因考虑了得和失2 方面的不确定信息，使得评价结果比传统的多属性决策方法(MCDM)更合理和稳定. 从而引起学者的关注，并将其应用于多属性决策[12-13]，2020 年廖虎昌等[14]继而研究了考虑专家偏好特征多属性群决策问题的基于Choquet 积分的犹豫模糊得失优势度评分方法. GLDS 虽应用诸多的模糊环境中，但很少有学者关注基本不确定信息软集的研究. 本文在提出基本不确定信息软集得失优势度评分方法的基础上，研究了其多属性决策. 同时，考虑到决策者在决策时对所选择方案的个人期望和前景，以及属性之间的相互作用，提出并研究了基于前景理论的不确定信息软集的得失优势度评分方法及其多属性决策. 最后给出了算例.

1 定义及说明

称f:[0,1]n→[0,1] 为输入向量x(n)的聚合函数，是指其满足：

2 基本不确定信息软集GLDS 方法

表1 基本不确定信息软集的表格表示Tab. 1 Tabular representation of a soft set of basic uncertain information

为基本不确定信息软集 (S,E) 在U上的基本不确定信息软矩阵.

由吴兴利等于2019 年所提出的得失优势度评分方法（GLDS）[10]，在属性决策中因考虑了得和失2 方面的不确定信息，使得评价结果比传统的多属性决策方法（MCDM）更合理和稳定，其主要方法是使用优势流函数获得备选方案之间的优势度. 同时，考虑每个备选方案的群效用值和个体悔恨值.

加权算法算子表示的是选择方案的大多数性能，但是对于一个备选方案，由于完全弥补效应，一些属性上差的性能可以由其他属性上好的性能弥补，因而不能选择在属性上性能太差的方案，即使它整合后性能是好的. 为了克服这个问题，计算备选方案ui关于所有属性的损失优势度评分，即总的损失优势度评分为

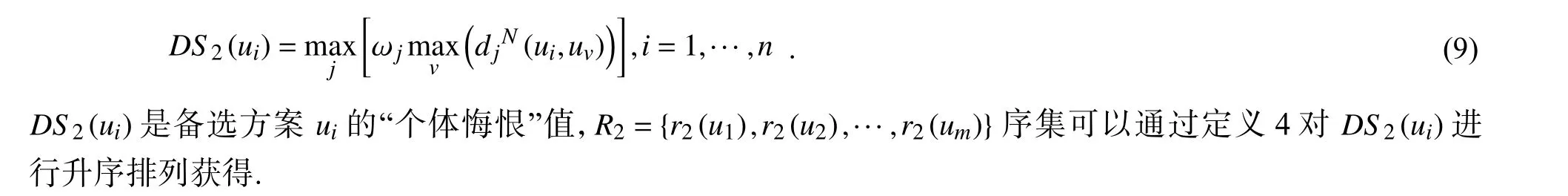
步骤 4 将2 个聚合模型得到的结果聚合为一个整体，若仅聚合总获得优势度评分和总损失优势度评分，则2 个聚合模型的保序性较差，且很难选择合理的权向量来度量2 个模型的权重. 若仅整合由2 个模型得到的序集，则很难准确地表达备选方案之间的差异，从而结果容易产生偏差. 为了增加整体的鲁棒性，需考虑优势度得分和隶属的序集. 将隶属的序集转化为每个备选方案优势度得分的权重，继而获得每个备选方案的总体得分，即

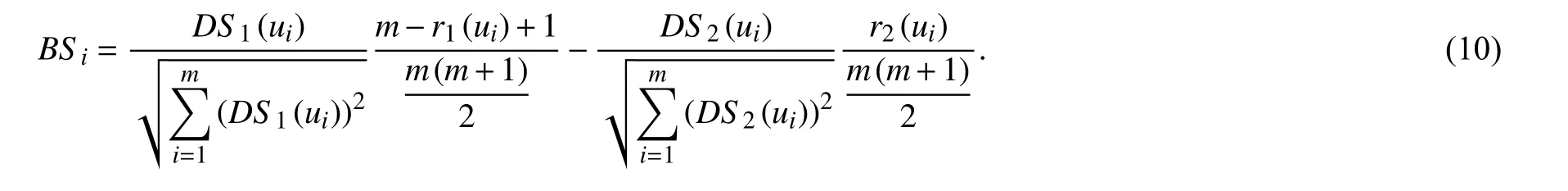
步骤 5 根据备选方案总体得分对备选方案进行排序择优.

3 基于前景理论的不确定信息软集的得失优势度评分方法

前景理论[17-18]的基本研究单元是前景，表示各种风险结果. 在多属性决策过程中，表示决策者对各种“前景”的排序择优. 在前景理论中，价值函数起到重要作用，表示决策结果和预期的差异程度，即相对于参照点的益损情况，是一个相对量，其表达式如下：

在实际的MDCM 问题中，评估过程中涉及相互关联的属性，基于Sugeno 提出的模糊测度[19], Choquet积分作为聚合算子对解决多属性决策问题中属性关联问题具有重要作用[20-21]. 由于相互关联的属性，则很难得到最优解，于是Yu 提出了折中解[22]而不是最优解来解决这个问题，主要思想是在正理想解(PIS)和负理想解(NIS)之间寻找一个折中解. 在本节中，我们提出在基本不确定信息环境下的折中值函数，利用该折中值函数，提出了一种综合的距离测度.

在规范化前景决策矩阵中正理想解(PIS)为：

由综合的距离测度，我们提出关于BUISS 的新的优势流函数，定义如下

4 实例分析与验证

本节利用BUISS 的GLDS 方法解决一个实际的最优绿色企业选择问题[10].

经济的快速发展提高了人们的生活水平，但造成了资源枯竭，环境污染和生态破坏. 可持续发展对人类的生存具有重要意义，即要求建立绿色企业，从设计、制造、销售到回收再利用都要满足特定的环境要求. 为了促进绿色企业的创建，中国某市决定从4 个候选企业u1，u2，u3，u4中选出一个最优的绿色企业. 评价属性为绿色产品与服务e1( 效益型属性)、绿色研发与创新e2( 效益型属性)、环境罚款与支出e3(成本型属性)，邀请3 位专家D1，D2，D3组成小组进行评估. 3 位专家的权向量为Z=(0.3,0.3,0.4)，3 位专家用BUISS来评估4 个绿色企业，其中决策矩阵为D11，D12，D13， 对应的前景决策矩阵为V11，V12，V13，规范化前景决策矩阵为V21，V22，V23.

根据提出的基于前景理论的基本不确定信息软集的得失优势度评分方法解决绿色企业选择的MCDM 问题，决策过程如下：

步骤 1 在规范化前景决策矩阵V21，V22，V23中，得到PIS 和NIS，从而确定优势流，设 λ =1，表示对损失敏感的中值，设 ω =0.5，计算对应的优势流；

步骤 2 由式(17)，对总优势流进行归一化处理，可得备选方案ui关于备选方案uv的归一化优势流，结果如表2～4 所示；

表2 属性 e1 下一个备选方案关于其他备选方案的归一化优势流Tab. 2 The normalized dominance flows of one alternative with respect to another under criterion e1

步骤 3 确定模糊测度，假设属性ej的模糊测度为 µ(e1)=0.4， µ(e2)=0.2， µ(e3)=0.3，可得交互指数λ=0.383， 从而 µ (e1,e2)=0.631， µ(e1,e3)=0.746， µ(e2,e3)=0.523,µ(e1,e2,e3)=1.

步骤 4 由(19)式，计算备选方案在不同属性下的总获得优势度得分，见表5.

表5 备选方案在不同属性下的获得优势度得分Tab. 5 The gained dominance scores of the alternatives under different criterion

步骤 5 由(20)式，计算备选方案在不同属性下的总损失优势度得分，见表6.

表6 备选方案在不同属性下的损失优势度得分Tab. 6 The lost dominance scores of the alternatives under different criterion

步骤 6 由(21)式将总获得优势度得分和总损失优势度得分进行聚合，求得备选方案的总得分分别为BS1，BS2，BS3，BS1. 根据总体得分，对备选方案进行排序并且选择最优的绿色企业，计算得BS1=〈0.5024;0.7701〉，BS2=〈0.5043;0.7760〉，BS3=〈0.4416;0.7794〉，BS4=〈0.4623;0.7945〉，根据定义4 对总体得分进行排序，得BS1≥BS2≥BS4≥BS3， 从而可选择的最优绿色企业为u1.

专家D1的决策矩阵和期望矩阵分别为：

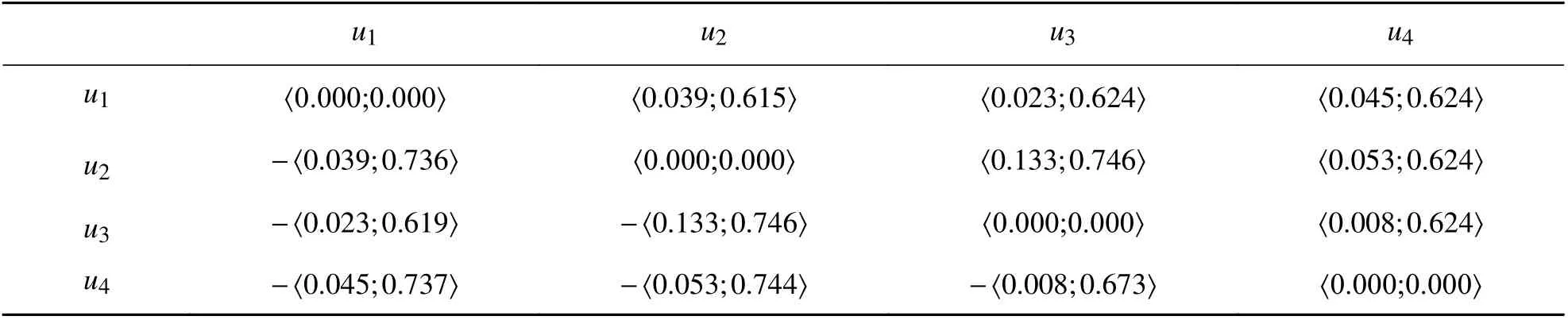
表3 属性 e2 下一个备选方案关于其他备选方案的归一化优势流Tab. 3 The normalized dominance flows of one alternative with respect to another under criterion e2

表4 属性 e3 下一个备选方案关于其他备选方案的归一化优势流Tab. 4 The normalized dominance flows of one alternative with respect to another under criterion e3

5 对比分析

为了表明提出方法的有效性，本文研究了基本不确定信息软集得失优势度评分方法，进一步提出基于前景理论的基本不确定信息软集的得失优势度评分方法及其多属性决策. 2 种方法在排序上存在一定的差异，基于前景理论的基本不确定信息软集的GLDS 评分方法得到的最差方案是u2， 最优方案是u1，基于基本不确定信息软集的GLDS 评分方法得出最差方案是u3， 最优方案是u4. 究其原因，基本不确定信息软集的GLDS 忽视了决策过程中属性间的相互依赖性和专家在决策时的心里偏好特征. 在实际的多属性决策问题中都包含这类特征，而基于前景理论的基本不确定信息软集的GLDS 评分方法，假设属性间是相互依赖的，并且专家完全理性的假设是无效的，因此该方法在实际生活中更具合理性. 此外，GLDS 方法是一种更有效和稳定的决策方法，避免了选择在某些属性下性能太差的方案，考虑了得和失2 方面不确定的内容，且结果更为稳定合理.

6 结论与展望

本文研究了基本不确定信息软集得失优势度的评分方法，考虑到决策者在决策时对所选择方案的个人期望和前景，以及属性之间的相互作用，进一步给出了基于前景理论的不确定信息软集的得失优势度评分方法，解决了多属性决策问题中各方案的排序择优. 以选择最优绿色企业为例，表明了该方法的可行性和适用性. 随着对多属性问题的研究，结合基本不确定信息软集和其他决策方法包括TOPSIS 方法，参数约简等将是我们下一步的工作. 由于基本不确定信息软集是一个新颖的概念，对于BUI 之间的运算以及在基本不确定信息背景下的群决策问题中，具有不同长度决策信息的BUI 集合或不同维数的BUI 向量的应用研究，尚在思考中.