耦合节点选择对网络交通动力学的影响分析

景兴利 胡茂彬

(1.济源职业技术学院，河南 济源 459000)(2.中国科学技术大学 工程科学学院，合肥 230026)

0 前 言

随着经济和社会的发展，交通拥堵问题越来越严重。如何解决交通拥堵问题，提高交通效率，一直是交通问题研究的热点。在过去的20多年里，学者们致力于复杂网络框架下的交通拥堵问题，将真实网络中传输或移动的旅客、汽车、飞机甚至是信息抽象为复杂网络中移动的单元以揭示交通问题的机理。研究表明，交通拥堵问题的形成与交通网络结构密切相关[1-2]。为了提高网络通行能力，减少交通拥堵，学者们提出了一系列措施用以改善网络通行状况，包括改变网络结构、设计更好的路由策略、优化交通资源配置等[1，3-10]。然而，目前的大多数研究都集中于孤立网络的建模和分析。现代网络系统中包含很多子网络或子系统，且它们之间又互相联系[11-12]。例如，城市交通网由道路网和地铁网组成，运输网由铁路网和航空网组成。耦合网络中的交通问题研究将为真实网络中交通拥堵治理提供一定的思路。学者们将单层网络的交通动力学过程描述为旅客按照路由引导从起点流向终点的过程[13]。将该交通动力学过程的概念推广到耦合网络，即成为耦合网络的交通动力学过程，但耦合网络的交通动力学特性与单层网络有着明显的不同[14-19]。Zhuo等人研究了物理层-逻辑层耦合网络的交通动力学特性，发现物理层越同构，网络的整体通行能力越大[20]。Morris等人研究了一个空间耦合网络的交通输运过程，发现随着耦合强度增加，输运的平均最短路径长度随之减小[21]。Sole-Ribalta等人研究了一个标准化多层网络模型的交通动力学特性，认为网络层的耦合强度和耦合方式对多层网络的通行能力有显著影响[22]。Gao等人提出了考虑网络局域信息和不同层间速度分布的有效路由策略，可以通过调节网络的平均度和层间速度分布提高耦合网络的通行能力[23]。

现有研究一般是基于随机选择节点进行耦合而生成网络，而不同耦合机制将对其网络结构和交通动力学特性产生影响[20-23]。本次研究提出两种新的网络耦合机制：选择度大节点进行耦合和选择度小节点进行耦合，并分别将其与随机耦合机制对网络交通通行能力的影响进行对比。为了进一步揭示这3种不同机制生成的耦合网络的动力学特性，分析了其中的平均传输时间(〈T〉)、平均传输距离(〈h〉)和层间平均转换次数(〈n〉)等运行指标。研究结果表明，选择度小节点进行耦合，可以达到更高的通行能力，并减少交通拥堵。本次研究为设计更加高效的交通传输网络提供了一种新思路。

1 模型的建立

1.1 网络模型

假设耦合网络由低速层网络A和高速层网络B两个子网络组成[14，23]。由于高速层网络的建设成本较高，所以其网络规模小于低速层。例如铁路-航空网，航空网的建设成本高于铁路网，铁路网的规模大于航空网，而航空网的旅行速度(成本)大于铁路网。在此应用Barabási-Albert(BA)网络模型[24]建立节点总数为NA的低速层子网络A，应用Erdö-Rényi(ER)网络模型[25]建立节点总数为NB的高速层子网络B，NA>NB。

(1)随机选择节点进行耦合。首先，构建具有NA个节点的子网络A；然后，在子网络A中随机选取NB个节点一一进行复制，将其作为子网络B的节点；最后，将子网络B的节点按照ER网络模型生成子网络B[14，20，23]。

(2)选择度大节点进行耦合。复制子网络A中的前NB个度大的节点作为子网络B的节点，并相应生成子网络B。

(3)选择度小节点进行耦合。复制子网络A中的前NB个度小的节点作为子网络B的节点，并相应生成子网络B。

图1所示为在不同耦合机制下生成的耦合网络。图中的实线圆圈表示子网络A的节点，虚线圆圈表示子网络B的节点(以下各图相同)。每个圆圈中都标注有该节点的属性字符。例如，一个圆圈中标注有“6(1)”，表示该节点的度为6，在该子网络中所有节点度按照从大到小进行排序，该节点位列第1。在图1a中子网络B为从子网络A中随机选择的节点经复制而生成的耦合网络；图1b中子网络B为从子网络A中选择度大节点经复制而生成的耦合网络；图1c中子网络B为从子网络A中选择度小节点经复制而生成的耦合网络。

图1 不同耦合机制生成的耦合网络

1.2 交通模型

假设子网络A的每个节点都可以产生和输运旅客，而子网络B的节点仅用于输运旅客。旅客在耦合节点处可以通过层间连边变换旅行的网络层。这里假设层间转换不消耗时间，每个节点在每个时间步发送旅客的能力为C。假设子网络A节点和子网络B节点的旅客发送能力相等且均等于1，即CA=CB=1。由于节点处理能力有限，每个节点都需要一个缓冲队列来容纳等待处理的旅客。假设缓冲区有足够的长度空间容纳滞留旅客，在处理每个队列的旅客时遵循先进先出的原则。旅客在耦合节点处的输运方法见图2，圆圈中的数字为节点编号。在〈T〉=1时间步，按照旅客到达节点6的先后顺序进行排队，假设旅客a位于队首，按照一定的导航策略，a的输运路径为：…→6→6"→4→…；在〈T〉=2时间步，按照先进先出及每个节点在每个时间步的旅客发送能力CA=1的原则，节点6仅能将旅客a输运到6"处，由于6与6"为耦合节点，那么旅客a将直接被输运至节点4处。耦合网络上的交通传输过程可以被描述如下：每个时间步，在子网络A上产生R个旅客，他们的出发点和目的地节点分别为在子网络A上随机选择的不同节点。每个旅客按照既定的路由策略从出发点到达目的地节点，如果到达目的地节点，则从网络中移除。显然旅客从出发点i到达目的地节点j的路径有很多，这里以Yan、Gao等人提出的有效路由策略作为旅客的传输路径Pi→j进行导航[4，23]：

图2 耦合节点处旅客输运方法示意图

(1)

式中：αF(αF>0)为旅客在F(F∈{A，B})层传输速度的调控参数，αF越小则在相应层的传输速度越快;kx为节点x的度；l为路径长度；θF为旅客在F层传输时，通过节点度来控制传输偏好的调控参数。旅客在从i到j的路径中选择旅行成本最小的路径：当θF<0(θF>0)时，旅客将优先选择F层中选择度大(小)的节点进行传输;当θF=0时，为最短路径路由策略。在最短路径路由策略中，网络拥堵总是最先出现在中心(Hub)节点，Yan等人在单层网络上通过改变θ值，引导旅客向选择度小节点传输，提高了网络的通行能力[4]。在此，仅对θF≥0的情况进行分析。按照上述交通传输过程的描述，旅客的输运过程算法流程如图3所示。

图3 旅客在网络中的输运算法流程图

网络的最大通行能力可以通过旅客临界产生率Rc来度量。Rc可以通过分析序参量η得到[4]：

(2)

ΔNp=Np(t+Δt)-Np(t)

式中：Np(t)为在t时间步时网络中的旅客总数。〈ΔNp〉表示对所有的仿真时间窗口Δt取平均。当RRc时，η>0网络为拥堵状态。相变点R=Rc为网络交通为自由流状态和拥堵状态的临界值，可用于表征网络的通行能力。

2 仿真结果及分析

基于有效路由策略,分别对3种不同机制耦合网络的交通动力学特性进行仿真分析。耦合网络节点总数(N)为2 000，子网络A的节点数(NA)为1 500，子网络B的节点数(NB)为500。A、B子网络的平均度相等，即==6。对于单层网络的有效路由策略[4，20]，θA=1.0时，网络可取得最大临界旅客产生率。根据对αF的定义，αB/αA可调控旅客在两层网络中的传输速度，在以下仿真过程中不作特殊说明时设αA=1.0，θA=1.0，通过调控其他参数来分析不同耦合网络的交通动力学特性。每次仿真模拟系统运行总计20 000个时间步。

图4为3种不同机制下生成的耦合网络采用有效路由策略时，取不同的调控参数αB和θB对应的交通流相变情况的仿真结果(Random:随机选择节点进行耦合;Small First:选择度小节点进行耦合;Large First:选择度大节点进行耦合)。选择度大节点进行耦合，当αB=0.2，θB=1.5时，取得最大临界旅客产生率Rc≈129；选择度小节点进行耦合，当αB=0.1，θB=1.6时，取得最大临界旅客产生率Rc≈159；随机选择节点进行耦合，当αB=0.4，θB=1.2时，取得最大临界旅客产生率Rc≈138。因此，选择度小节点进行耦合，其网络具有更优的通行能力。

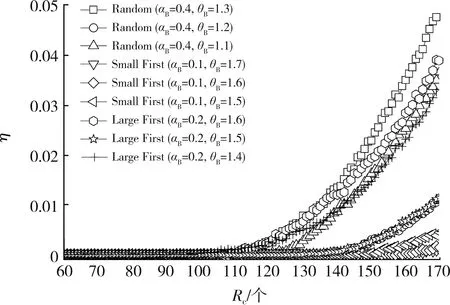
图4 不同耦合机制下的网络交通流相变情况仿真结果

图5为临界旅客产生率随不同调控参数的变化情况。由图5a知，选择度大节点、随机选择节点进行耦合时，Rc随着αB增大均先增大后减小；选择度小节点进行耦合时，Rc随着αB增大而减小。由图5b知，3种不同耦合机制下Rc均随着θB增大先增大后减小。这进一步证明，选择度小节点进行耦合其网络可取得最优通行能力。研究表明，在相同条件下，网络度分布越均匀，Rc越大[24]。选择度小节点进行耦合生成的网络度分布最均匀，随机选择节点进行耦合次之，而选择度大节点进行耦合生成的网络度分布最不均匀。因此，选择度小节点进行耦合时，其网络能获得更大的通行能力。

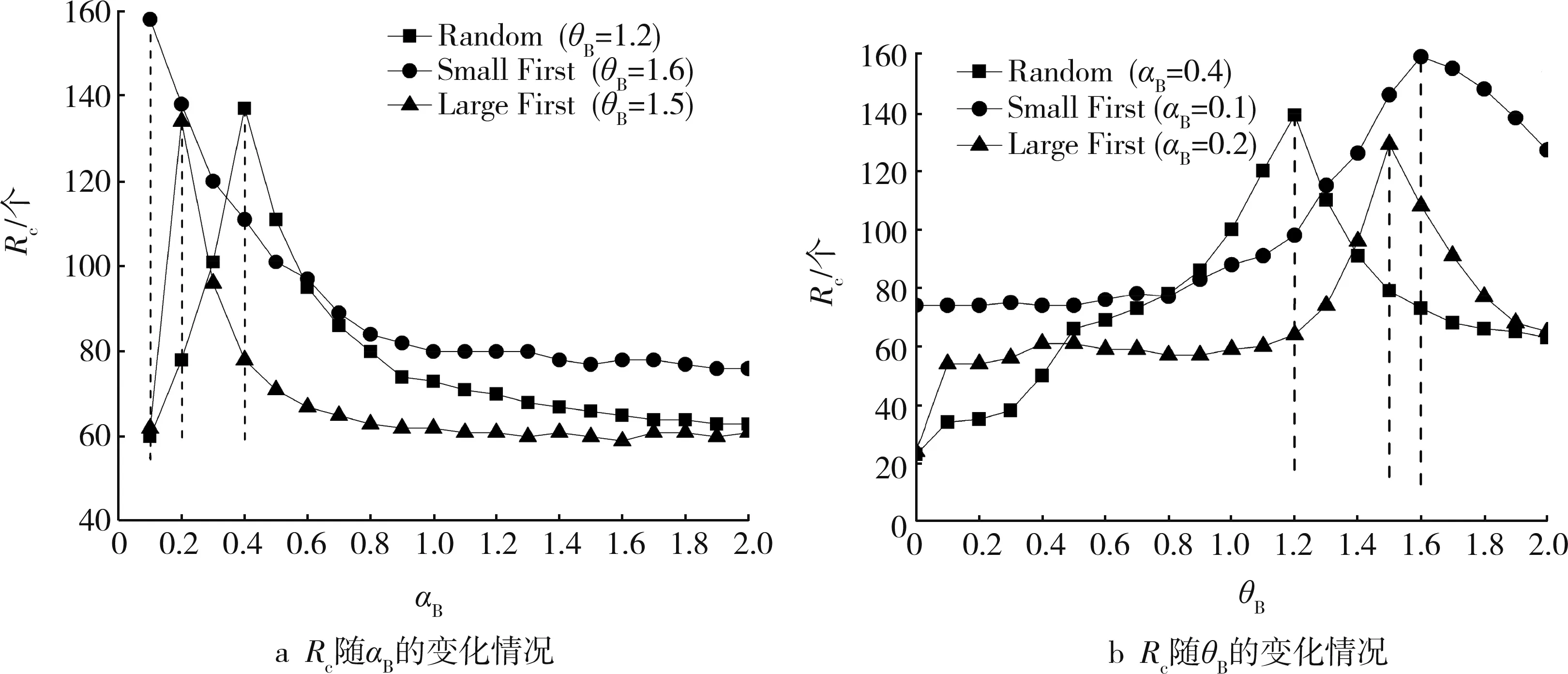
图5 临界旅客产生率随不同调控参数的变化情况

进一步对耦合网络的平均传输时间(〈T〉)、平均传输距离(〈h〉)、层间平均转换次数(〈n〉)等交通动力学特性刻画指标进行分析[26-29]，结果如图6、图7所示。

平均传输时间定义为：

(3)

式中：m为到达目的地点的旅客总数；Tp为旅客p的旅行时间。为了提高网络通行能力，必须降低传输时间。

平均传输距离定义为：

(4)

式中：hp为旅客p从始发点到目的地点所经过的节点总数。平均传输距离受到调控参数αF和θF的影响。

层间平均转换次数定义为：

(5)

式中：np为旅客p在完成从出发点到目的地点的传输过程中在A、B层间转换的次数。

在自由流状态下(Rc=10)，3种不同机制下生成的耦合网络取最优θB时，不同调控参数αB对应的〈T〉、〈h〉、〈n〉等指标的变化情况如图6所示。3种耦合网络随着αB的增大，〈T〉和〈h〉均先迅速减小而后增大；在各耦合网络最优αB值处，分别取得了较小的〈T〉和〈h〉值。由图6(c)知，随着αB增大，3种耦合网络的〈n〉均先单调下降后趋于稳定。〈n〉在趋于稳定前，选择度大节点进行耦合的网络〈n〉对αB的变化最为敏锐，其次为选择度小节点进行耦合的网络。当选择度小节点进行耦合时，在最优值αB=0.1处，〈n〉≈2.07；当选择度大节点进行耦合时，在最优值αB=0.2处，〈n〉≈1.48；当随机选择节点进行耦合时，在最优值αB=0.4处，〈n〉≈1.36。在相同条件下，当0.2≤αB≤2时，随机选择节点机制下网络传输过程层间转换较另外两种机制下传输更加频繁，但其对应的〈T〉与〈h〉并非最小值。

图6 不同交通动力学特性刻画指标随调控参数αB的变化情况

在自由流状态下(Rc=10)，3种不同耦合网络取最优的αB时，不同调控参数θB对应的〈T〉、〈h〉、〈n〉的变化情况如图7所示。随着θB的增大，〈T〉、〈h〉均先减小而后增大。在各耦合网络的最优θB值处，取得了较小的〈T〉和〈h〉值。由图7(c)知，在相同条件下，选择度小节点进行耦合，〈n〉始终保持较大值。当选择度大节点进行耦合时，由于BA、ER网络的结构性质，耦合节点在BA层的邻居节点度较大，而其在ER层的邻居节点度较小(平均度约为6)。较小的θB不能改变度大节点被选作传输路径的优势，表现为θB<1范围内，αB对〈n〉的影响较小。

图7 不同交通动力学特性刻画指标随不同调控参数θB的变化情况

3 结 语

耦合网络的交通动力学是网络交通领域研究的热点问题。为提高网络的通行能力，提出了两种新的节点选择耦合机制。研究结果表明，包括常见的随机选择节点机制在内，选择度小节点进行耦合生成的网络能够可以减少交通拥堵，获取更大的网络通行能力。

为揭示其中的机理，进一步对耦合网络的〈T〉、〈h〉、〈n〉等交通动力学特性刻画指标进行了分析。研究结果表明，选择度小节点进行耦合生成的网络在〈T〉、〈h〉等方面较另外两种耦合机制有明显优势。