气驱油藏单井动态储量与可采储量计算新方法
郑冰洋 胡书勇
(西南石油大学 石油与天然气工程学院,成都 610500)
0 前 言
目前,水驱特征曲线已经广泛应用于国内外水驱油田的开发指标预测中,但气驱油藏的气驱特征曲线理论却发展缓慢。其原因是,在油藏注气开发中后期储层内部形成油气两相渗流,给油藏生产动态分析及可采储量预测带来较大困难。所以,一般采用油藏数值模拟技术及室内实验方法来评价油藏注气开发效果[1-3]。
对于气驱油藏,有关学者根据水驱特征曲线推导过程,建立了4种气驱特征曲线[4-8],有效地解决了利用水驱特征曲线来评价气驱开发效果的不科学性问题。油气两相相对渗透率曲线的形态反映了气驱油的渗流特征,其精确度决定了后续气驱特征曲线拟合气驱油藏生产规律的精确度。2015年,童凯军等人基于油气两相渗流规律和物质平衡方程理论,建立了新型气驱特征曲线,并论证了新型气驱特征曲线的适用性[9]。2017年,李珂等人针对油气两相相对渗透率曲线的先“凸”型下降后“凹”型下降的非指数式特征,提出了一种新型油气两相相对渗透率曲线的表达式,并建立了新型非指数式气驱特征曲线[10]。同年,吕成远等人针对CO2非混相驱的油、气、水三相相对渗透率特征和原油黏度动态变化特征,建立了分段式气驱特征曲线[11]。2018年,苑志旺等人基于稳定渗流理论,建立了新型半对数气驱特征曲线[12]。2019年,张迎春等人基于油气两相渗流规律和物质平衡方程理论,建立了新型气驱特征曲线,并推导了气油比与采出程度、气油比上升率与采出程度的指数型关系式[13]。同年,顾文欢提出适用于高气油比阶段油气两相相对渗透率曲线的新型表达式,建立了开发中后期气驱油藏的新型气驱特征曲线[14]。
针对低含气和高含气阶段,油气两相相对渗透率比值与含气饱和度在半对数坐标中出现明显偏离直线关系的问题[14],本次研究拟采用二项式方程对全阶段的油气两相相对渗透率比值与含气饱和度的关系曲线进行描述分析,并以油气两相渗流规律和物质平衡方程为理论基础,推导一种新型气驱特征曲线方程,进而根据该方程拟合参数建立单井动态储量与可采储量计算方法。以W气驱油藏P1井为例,验证新型气驱特征曲线对单井动态储量与可采储量计算的可靠性和准确性,以便更有效地进行注气开发油藏的生产动态分析和开发指标预测。
1 Kro/Krg与Sg关系
常规气驱特征曲线的推导,是基于含气阶段油气两相相对渗透率比值(Kro/Krg)与含气饱和度(Sg)在半对数坐标中的线性关系(见图1)[9],此方法忽视了低含气和高含气阶段Kro/Krg与Sg在半对数坐标中出现的明显偏离直线的问题。为了解决这一问题,取W气驱油藏的岩心,在油气非混相条件下测得该岩心油气相对渗透率数据(见图2),采用多项式方程拟合ln(Kro/Krg)与Sg的关系曲线(见图3—图6)。对全阶段的Kro/Krg与Sg关系曲线进行描述分析,拟合结果如表1所示。

图1 线性拟合曲线
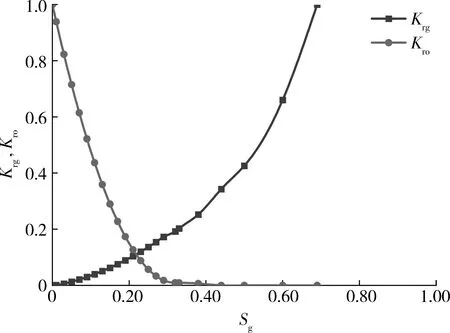
图2 油气相对渗透率曲线
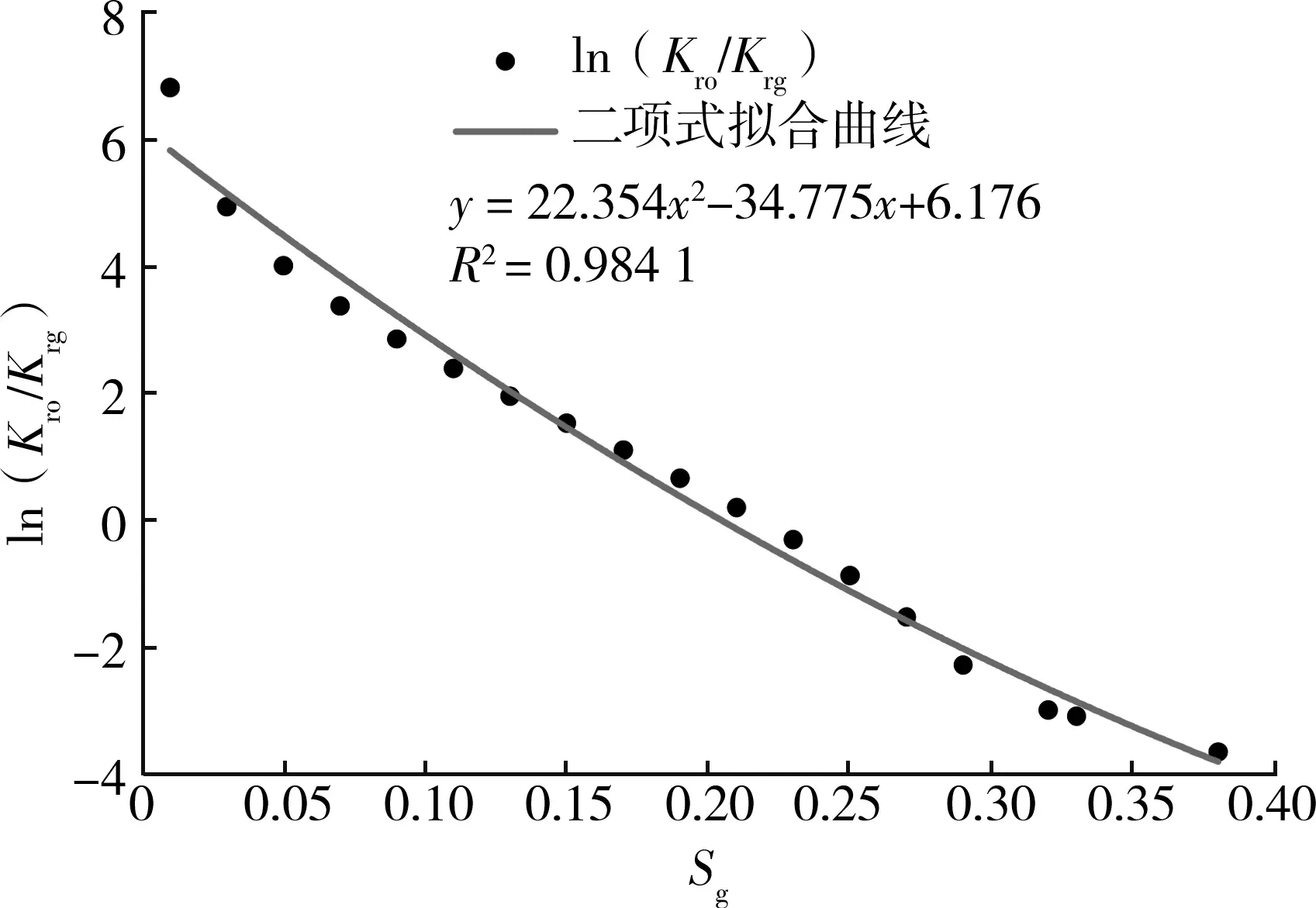
图3 二项式拟合曲线

图4 三项式拟合曲线

图5 四项式拟合曲线
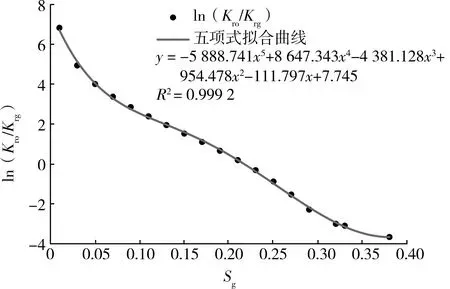
图6 五项式拟合曲线
根据表1所示,相关系数(R2)随着多项式数量的增加而增大,拟合精度提高,但多项式越多,后续气驱特征曲线方程的推导越困难。研究发现,采用二项式方程描述ln(Kro/Krg)与Sg的关系,在保证较高拟合精度的前提下,可以最大限度地简化后续气驱特征曲线方程的推导过程,即:
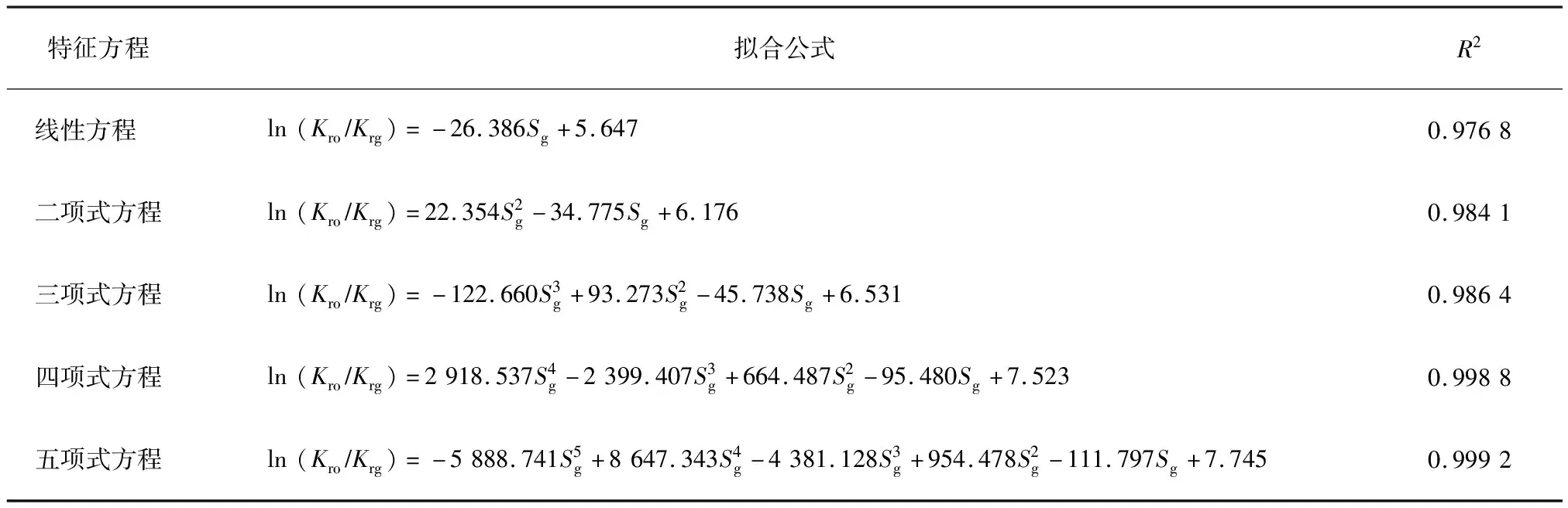
表1 ln(Kro/Krg)与Sg关系曲线拟合结果
(1)
式中:Kro——油相相对渗透率;
Krg——气相相对渗透率;
Sg——含气饱和度;
a、b、lnc——二项式方程回归系数。
对式(1)的等号两边进行运算,得到气驱油藏油气两相相对渗透率比值与含气饱和度的指数关系式,如式(2)所示:
(2)
2 新型气驱特征曲线推导
2.1 假设条件
(1)地层恒温,温度保持120 ℃;
(2)储层为均质;
(3)忽略毛管力及重力;
(4)油藏压力补充及时,忽略流体性质及流体参数变化;
(5)地层仅存在油气两相渗流,符合达西定律,地层水以束缚水形式存在。
2.2 油气两相渗流规律
在地层条件下,油气两相处于稳定渗流时,根据达西定律,油气两相流量比值与油气两相相对渗透率比值的关系为:
(3)
式中:qg——地层条件下气相流量,m3;
qo——地层条件下油相流量,m3;
μo——地层条件下原油黏度,mPa·s;
μg——地层条件下天然气黏度,mPa·s。
其中,油气两相地下流量与地面流量的关系为:
(4)
式中:qgsc——地面条件下气相流量,m3;
qosc——地面条件下油相流量,m3;
Bg——天然气体积系数;
Rsi——原始溶解气油体积比。
将式(4)和式(2)带入式(3),可得到:
(5)
将式(5)变形得到qgsc与qosc的转化关系:
(6)
将式(6)方程两边同时除以qosc,得到生产气油比与含气饱和度的关系式:
(7)
式中:Rgo——生产气油体积比。
对式(7)进行变形,等号两边同时取对数,得到ln(Rgo-Rsi)与Sg的关系式:
(8)
2.3 物质平衡方程
根据物质平衡方程,任一时刻油藏的含油饱和度为油藏中剩余油体积与油藏孔隙体积之比:
(9)
式中:So——含油饱和度;
N——原油地质储量,104m3;
Np——累计产油量,104m3;
Bo——原油体积系数;
Boi——原油原始体积系数;
Swi——束缚水饱和度。
在注气驱油的过程中,含气饱和度可以表示为:
Sg=1-Swi-So
(10)
将式(9)带入式(10)可得任一时刻油藏的含气饱和度为:

(11)
2.4 新型二项式气驱特征曲线
将式(11)带入式(8),得到注气开发油藏的新型二项式气驱特征曲线:
(12)
将式(12)化简为:
(13)
其中,
(14)
2.5 单井动态储量与可采储量计算方法
根据式(13)中系数η1和式(1)中回归系数a,推导得到注气开发油藏的单井动态储量计算公式:
(15)
当单井达到经济极限的生产气油比Rgo,max时[9],根据式(13)中回归系数η1、η2、η3,推导得到单井的可采储量计算公式:
(16)
3 应用实例
以W油藏P1井为例,验证新型气驱特征曲线对单井动态储量与可采储量计算的可靠性和准确性。生产井P1注气开采后的生产动态数据如表2所示。根据表2中的累计产油量和生产气油比数据,绘制ln(Rgo-Rsi)与Np的关系曲线,并对常规气驱特征曲线和新型二项式气驱特征曲线进行拟合,将常规气驱特征曲线转化为气油比形式,如式(17)所示:

表2 W油田P1井注气开采后生产动态数据
ln(Rgo-Rsi)=D1Np+D2
(17)
拟合结果如图7、图8所示,新型二项式特征曲线和常规特征曲线的回归方程如表3所示。根据表3所示的气驱特征曲线回归方程,求得P1井每个时间步的累计产油量,计算其与实际累计产油量的误差(见表4)。由新型二项式气驱特征曲线计算的累计产油量误差远远小于常规气驱特征曲线,说明本次推导的新型二项式气驱特征曲线具有可靠性。

表4 根据不同气驱特征曲线计算的累计产油量与实际累计产油量误差

图7 新型二项式气驱特征曲线

图8 常规气驱特征曲线
由表1和表3可知,ln(Krg/Kro)与Sg的二项式方程系数分别为:a=22.354,b=-34.775,c=480.871;P1井的新型二项式气驱特征曲线的系数为,η1=4.337×10-4,η2=0.016,η3=2.928。将系数带入式(15),求得W油藏P1井动态储量为159.271×104m3。当P1井达到经济极限生产气油比为1 000.0时,由式(16)计算得到P1井可采储量为76.978×104m3。

表3 气驱特征曲线回归方程
4 结 语
以油气两相渗流规律和物质平衡方程为理论基础,推导并建立了一种新型二项式气驱特征曲线方程。方程更精确地描述了油气两相渗流规律,克服了常规气驱特征曲线无法准确描述低含气和高含气阶段Krg/Kro与Sg关系的缺点。
基于新型二项式气驱特征曲线,引入经济极限生产气油比,推导并建立了注气开发油藏的单井动态储量和可采储量计算方法。
应用实例表明,与常规气驱特征曲线相比,新型二项式气驱特征曲线对实际生产动态数据的拟合精确度更高,对气驱开发油藏的指标预测具有一定的实用性。

