考虑渗透率时变的边底水低渗油藏高速开发剩余油分布模式研究

陈 军 李仕芳 黄治梁 薛永超 王鹤楠 杨松林

(1.长庆油田分公司第十采油厂，甘肃 庆阳 745100；2.中国石油大学(北京)石油工程学院，北京 102249)

0 前 言

以长庆油田为代表的低渗透油藏经历了长期的水驱开发，大部分油田进入特高含水、低采出的关键时期，如何客观准确的预测剩余油分布规律是此类油藏二次开发的重点和难点。矿场实践表明，由于较高的采油速度和较强的边底水驱替冲刷，储层渗透率较开发初期发生明显变化，注入水的水化膨胀以及冲刷作用会造成地层微粒和黏土矿物的运移，油藏剩余油分布更加难以预测和表征，油藏二次开发面临巨大挑战[1-4]。因此，在预测长期水驱低渗油藏剩余油分布规律时，必须考虑渗透率随开发进程的变化。本次研究基于过水倍数与渗透率的变化关系，建立连续变化且具有方向性的表征模型，并综合油藏工程方法和油藏数值模拟技术，模拟低渗透油藏开发过程，预测剩余油分布规律，为长期水驱低渗油藏的二次开发提供支撑。

1 渗透率时变表征方法

1.1 表征方法

目前，渗透率时变表征方法主要有3种，一是单因素表征法；二是多因素表征法；三是水驱强度表征法。其中单因素表征法和多因素表征法均存在表征不连续、人为因素影响较大等问题[5-8]。而水驱强度表征法可以消除人为因素的影响，表征结果更为客观，同时该方法还可与油藏数值模拟相结合，对剩余油地挖潜具有重要指导意义，因此，水驱强度表征法应用较为广泛[9-13]。为了保证油藏中后期表征效果以及表征的方向性，结合目标区含油面积较小、网格尺寸较为确定等因素，最终选用基于过水倍数的渗透率时变表征方法。

过水倍数是指在一定注入强度下，流过单位体积储层的累积水量与该单位体积储层的孔隙体积之比。实际油藏中，注入水在不同方向上的流动是不同的，这将导致不同方向上的渗透率变化不一致。因此，在实际油藏计算时，应统计各个方向上的过水倍数，用油藏单元立方体图(见图1)加以说明。

图1 单元立方体图

网格(i，j，k)第n+1时刻x、y、z方向的过水倍数分别为：

(1)

(2)

(3)

式中：Vijk为网格(i，j，k)的孔隙体积，m3；Nx、Ny、Nz分别为x、y、z方向过水倍数；Qx、Qy、Qz分别为x、y、z方向过水量，m3。

则单元立方体过水倍数表达式为：

N=Nx+Ny+Nz

(4)

式中：N为过水倍数。

1.2 渗透率时变规律

选取目标油藏典型岩心样品，开展不同级别渗透率岩心的驱替实验，得到不同级别渗透率岩心的渗透率变化倍数(不同时刻渗透率与初始渗透率的比值)随过水倍数的变化曲线(见图2)。如图2所示，岩心渗透率变化倍数随过水倍数的增加而逐渐变小，由于初始渗透率不同，水驱前后渗透率变化趋势也不同。初始渗透率越小，高倍水驱条件下渗透率变化倍数越小，渗透率下降越明显，对储层伤害越大。

图2 岩心渗透率变化倍数随过水倍数的变化

对图2中的数据进行拟合，得到渗透率变化倍数与过水倍数表征方程：

K=19.00×10-3μm2时：

(5)

K=38.00×10-3μm2时：

(6)

K=48.00×10-3μm2时：

(7)

式中：K：渗透率，10-3μm2；Kx为x方向的时变渗透率，10-3μm2；Kx0为x方向初始渗透率，10-3μm2。

考虑到低渗透油藏较强的非均质性，根据油藏实际情况确定y、z方向渗透率，如下式所示：

(8)

式中：Ky为y方向时变渗透率，10-3μm2；Kz为z方向时变渗透率，10-3μm2。

2 渗透时变在数值模拟中的应用

2.1 油藏概况

里37区延9油藏位于鄂尔多斯盆地陕北斜坡上，油气分布受岩性—构造双重影响，整体表现为西低东高。储层岩性以长石质石英砂岩为主，平面呈条带状分布，油藏西部发育较强的边底水,厚度较大(最厚达42.7 m)；油藏东部由于砂层变薄、隔层变厚，边底水对其影响减弱。储层平均孔隙度15.8%、平均渗透率38.03×10-3μm2，属低孔低渗油藏。2012年10月油藏整体停产，各类完钻井总计48口，油藏开发指标如表1所示。

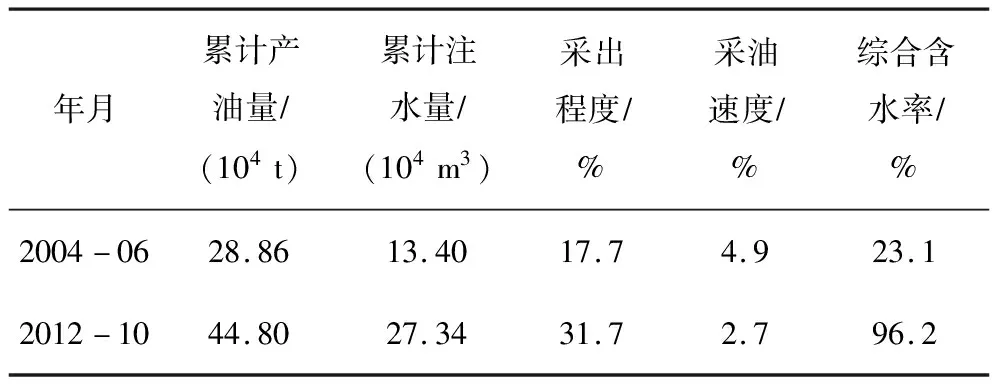
表1 油藏开发指标

2.2 过水倍数分析

应用tNavigator油藏数值模拟软件，通过累计过水量与孔隙体积的比值计算过水倍数。图3为过水倍数的三维图，由于西部边底水的存在，油藏西部受到较为强烈的冲刷，过水倍数较高。井点处由于冲刷较为充分，过水倍数较高，油藏内部由于隔夹层的存在，冲刷不充分，过水倍数较低。

图3 里37延9油藏过水倍数三维图

2.3 历史拟合效果对比

目前的数值模拟中，渗透率时变大都采用统一的物性时变模拟框架[14-18]，即全区采用一种时变规律。该区块实际平均渗透率为38.03×10-3μm2，图4为全区只考虑一种渗透率时变规律表征模型(式(6))的历史拟合结果。如图4所示，考虑一种时变规律的历史拟合效果优于未考虑渗透率时变的情况，但油藏开发后期模型拟合效果仍不理想。

图4 考虑一种渗透率时变规律表征模型的历史拟合结果

通过对过水倍数的分析可以看出，目标油藏非均质性较强，各部位冲刷不均匀。因此，在历史拟合过程中，应考虑多种不同的渗透率时变规律，即根据不同的初始渗透率，匹配不同的数学关系(见图2)。当初始渗透率小于20.00×10-3μm2时，应用式(5)的表征模型；当初始渗透率为20.00×10-3～40.00×10-3μm2时，应用式(6)的表征模型；当初始渗透率大于40.00×10-3μm2时，应用式(7)的表征模型。

图5为考虑不同级别渗透率时变表征模型的历史拟合结果图。按照初始渗透率的不同匹配不同时变规律的历史拟合效果要优于全区只考虑一种时变规律的情况。

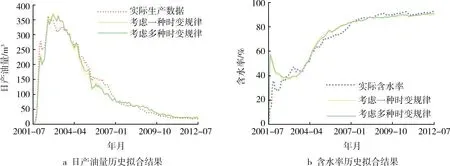
图5 考虑不同渗透率时变规律表征模型的历史拟合结果

3 剩余油分布模式

3.1 以边底水为主控因素

图6分别为2001、2012年油藏以边底水为主控因素的剩余油饱和度分布图。从图中可以看出：油藏西部及底部受边底水的影响较大，驱替充分；油藏东部及东北部附近受边底水影响较小，剩余油饱和度高，爬坡油富集。

图6 以边底水为主控因素的剩余油饱和度分布图

图7为以边底水为主控因素形成的爬坡油模式图。边底水从砂体底部推进，砂体上部驱替不充分，最终剩余油在边底水上部富集，形成爬坡剩余油。

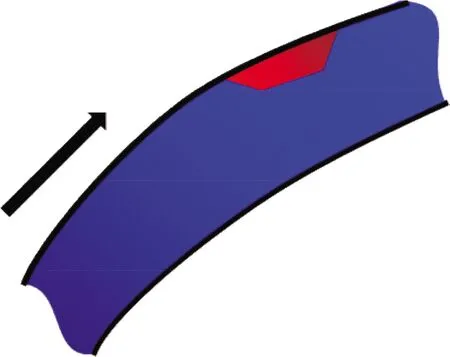
图7 爬坡油模式图

3.2 以局部构造为主控因素

图8为受局部构造影响的剩余油饱和度剖面图。由图8可知，剩余油主要集中在A井附近。这种情况主要受两方面的影响：一是在驱替过程中，水线沿着构造线逐步推进，但是推进范围会逐渐变小，位于构造高点处的油无法被完全波及，致使油藏构造高点处剩余油富集。二是当开发进行到中后期时，存在边底水或水驱效果较好区域附近的油井下部水淹比较严重，导致含水饱和度高，而构造高层位由于自身动用较小、含水饱合度低，剩余油饱和度较高，形成屋脊油。

图8 受局部构造影响的剩余油饱和度剖面图

图9为受隔夹层影响的剩余油饱和度剖面图。由图9可知，在夹层上部及下部形成屋檐油和阁楼油。这是由于隔夹层能够阻挡油气水的渗流，改变了波及效果，使得隔夹层附近的剩余油难以被驱替。

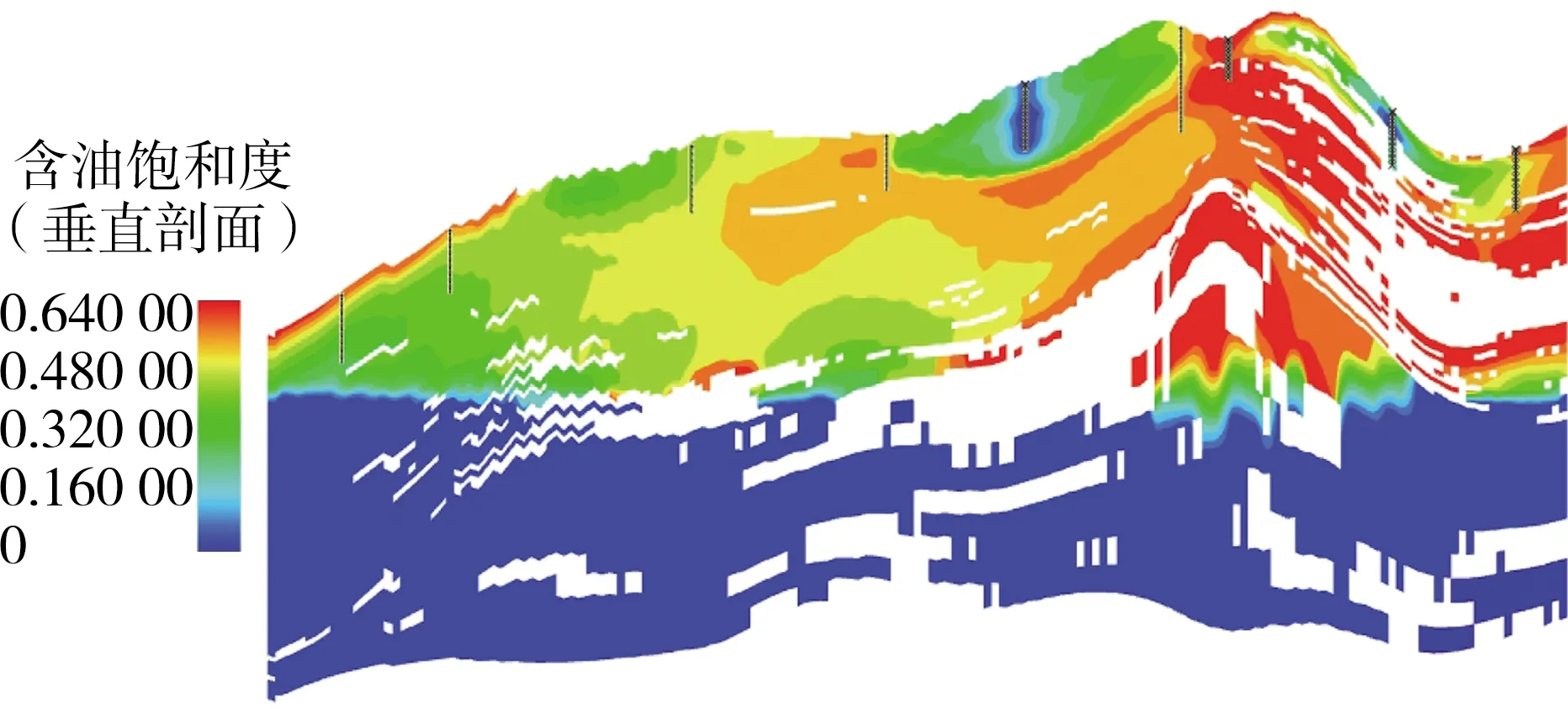
图9 受隔夹层影响的剩余油饱和度剖面图

图10为屋脊油、屋檐油、阁楼油模式图。由于受到局部构造的影响，剩余油通常富集在局部构造高层位及发育隔夹层的部位，形成屋脊油、屋檐油和阁楼油。

图10 屋脊油、屋檐油、阁楼油模式图

3.3 以井网不完善为主控因素

图11为受井网不完善影响的剩余油饱和度分布图。由于开发初期对地质条件认识不充分，导致油田注采系统不完善，开发效果不理想，剩余油在B、C等井网不完善的区域富集。

图11 受井网不完善影响的剩余油饱和度分布图

4 结 语

长期水驱开发的低渗透油藏,其渗透率会发生较大变化，在剩余油预测中应考虑储层渗透率时变特征。对于含油面积较小、网格尺寸较为确定的油藏，可以利用过水倍数表征渗透率时变。

对于非均质性较强的油藏，根据初始渗透率的不同匹配不同的渗透率时变规律，可以改善油藏高含水阶段的拟合效果。

根据渗透率时变的数值模拟结果，可以将剩余油分布模式归纳为3类：以边底水为主控因素的爬坡油，以局部构造和夹层为主控因素的屋檐油、屋脊油、阁楼油和以井网不完善为主控因素的井间油。