计及不确定性的风-柴-储组合微电网规划

张涛允，张玉刚，白文远，张广东，黄志勇，李岳

（1.国网甘肃省电力公司电力科学研究院，甘肃 兰州 730070；2.国网甘肃省电力公司，甘肃 兰州 730070；3.北京国网富达科技发展有限责任公司，北京 100160；4.福州大学电气工程与自动化学院，福建 福州 350108）

传统微电网通常由柴油发电机供电，然而柴油的高昂成本以及相对昂贵的、或不可能通过不同电网铺设输电线路的方式，促使偏远地区微电网供电要利用可再生能源。现已有大量关于微电网的运行和规划的研究[1-3]。在这方面，风能柴油系统代表着未来的研究方向。风电的一个主要问题是风的间歇性，由于风力涡轮机的有功功率波动，很难匹配负载生成平衡[4-5]。风、光等分布式电源出力与负荷功率的不确定性对微电网规划影响显著，文献[6-7]采用了鲁棒优化的方法来处理不确定性，但仅统计出风电、光伏发电以及负荷的大致波动范围。在孤岛运行的微电网中，风能的高渗透率可能会大大降低系统的运行可靠性，还必须考虑更多细节。此外，柴油发电机通常会保留在孤岛运行的微电网中，以控制系统的电压和频率[8]。目前，结合可靠性标准或经济考虑因素的独立电力系统的规划已在单独的工作中进行了研究。

储能系统（energy storage system，ESS）可以通过在低负载时存储能量并在高负载时释放存储的能量来减轻风力发电的不确定性，因此ESS 是未来微电网不可或缺的组成部分[9-11]。但是选择ESS 时应同时考虑可靠性指标和节省总成本，文献[12-13]的方法多集中在ESS 最佳固定大小选择上，但随着大规模ESS技术的发展，可以在几乎不受位置和大小限制的情况下安装储能设施。此外，储能系统的电池容量衰减现象在规划中长期被忽视，但ESS 的容量大小在整个时间跨度内被扩大可有效提高系统经济性。

综上所述，虽然关于含风电和储能系统的电力系统规划做了大量研究，但是关于风电-柴油机-储能系统的组合电力系统规划相关研究较少，且电网逐渐趋于饱和，电力系统的容量扩展规划在生产实际中更具有现实意义。因此，提出了一个含风-柴-储组合系统的微电网扩展规划模型，并采用了一种随机优化方法，以解决与风力发电和负荷相关的不确定性问题。在提出的方法中，使用蒙特卡洛模拟生成大量场景。优化模型所需的计算工作量是关于场景数的函数，提出一种场景削减方法，使原系统在较少的场景数下获得可接受的近似值，大幅减少了计算量。为了使孤岛运行的微电网的总成本降至最低，考虑了投资、运营、维护和停电成本。此外，除了柴油机和ESS 的实际限制外，在此优化过程中还必须满足可靠性限制。

1 蒙特卡洛随机规划

随机规划是一种数学优化问题，问题中的部分或所有参数由随机变量表示。当统计数据不足以支持随机优化时，场景分析是解决多周期优化问题的常用方法之一，每个场景都对应一个随机变量的结果[14-16]。在电力系统的运行和规划中几种优化方法已将情景分析用于不确定性分析，其中蒙特卡洛方法的主要思想是估计由场景定义的目标函数的期望值。蒙特卡洛方法的显著优势之一是达到指定精度水平所需的样本数量与系统大小无关，因此蒙特卡洛非常适合分析大型系统。

1.1 场景生成

场景是基于蒙特卡洛模拟生成的，风速、负荷预测误差以及柴油和风力发电机组的可用性是每种情况下必须指定的最重要的随机变量。历史时间序列的采样和使用统计模型是场景生成最常用的方法。

1.1.1 风力发电

为了模拟风速的随机性，使用了威布尔分布概率函数：

式中：v，I，C分别为风速、形状因子和比例因子。

风力发电机的风速的功率输出函数可表示为

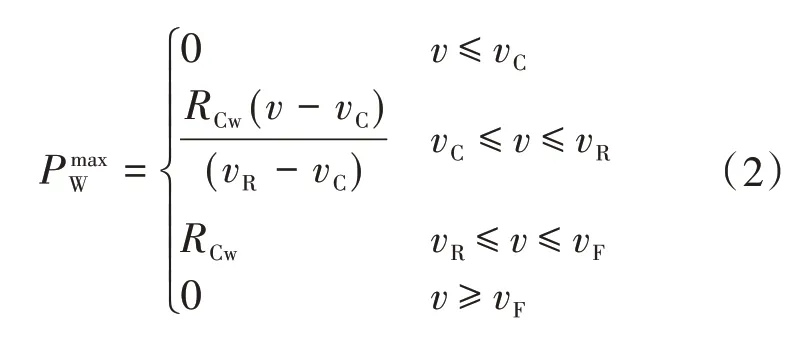
式中：RCw为额定电量；vC为切入风速；vR为额定风速；vF为切出风速。

1.1.2 风力和柴油发电的可用性

在场景生成中，必须为每个柴油机组和风力涡轮机计算在规划期间内的机组可用性，发电机组可用性状态的时间序列是基于其故障率和维修时间使用指数分布生成的。蒙特卡洛方法用于在计划时间范围内使用两阶段连续时间马尔可夫链模型来表示元件故障。

1.1.3 负荷预测不确定性

负荷预测需要足够的历史数据来确定代表误差的准确分布函数，可使用正态分布来模拟负荷预测的不确定性[17]。正态分布的均值描述了高峰负荷预测，正态分布可以划分为若干离散区间，每个区间对应的荷载概率等于区间的中点。为了模拟负荷预测误差，算例研究部分采用了7个区间的正态分布。

1.2 场景削减

减少场景的主要方法是根据随机分布之间的距离来控制适应度函数（作为概率指标），使用算法的详细信息如文献[18]所述。使用蒙特卡洛模拟生成方案，场景削减后将保留S个方案。场景削减过程一直持续到使用其余方案计算出的σLOLE将小于预定值。预定值通常为0.01～0.05，可表示为

式中：LOLEx为与场景x相关的失负荷时间期望，基于风电和柴油发电机组故障停电率计算；为S个场景的失负荷时间期望平均值；σfix为失负荷时间期的期望标准偏差。

2 规划模型

2.1 目标函数

考虑从场景削减算法中获得的每个场景的概率，以系统总成本最小为目标函数。系统总成本包括投资成本、运营成本、维护成本和停电损失费用，如下式所示：

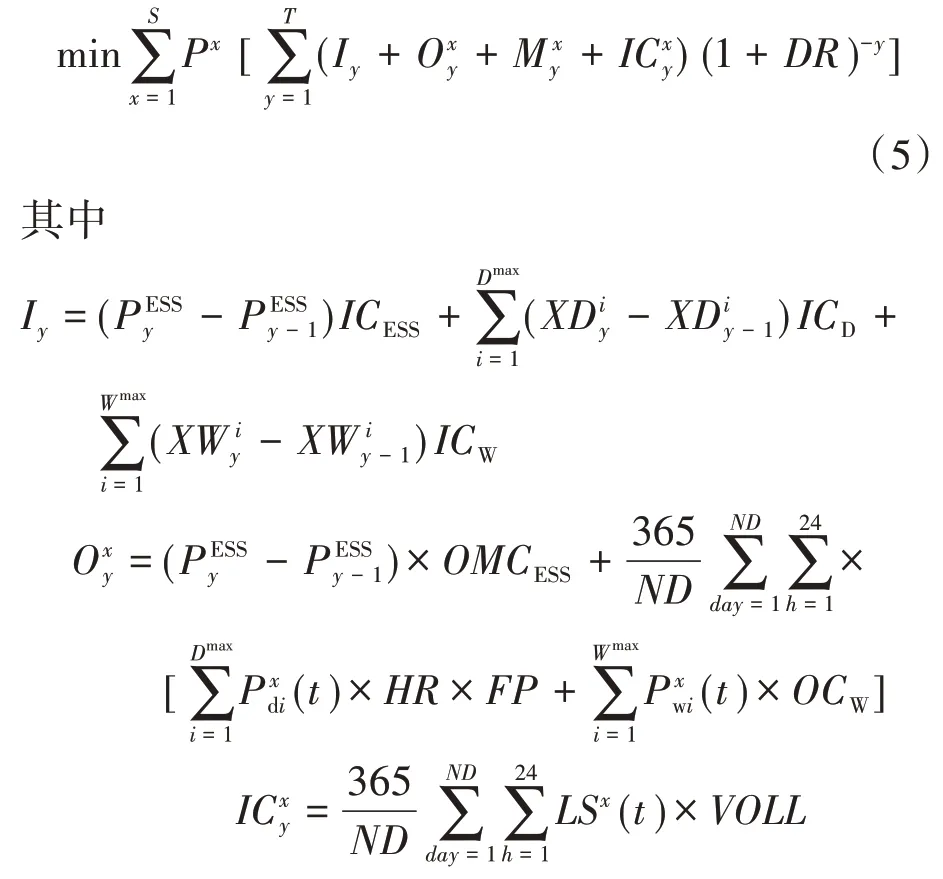
式中：Px为场景x的概率；T为规划总年限；Iy为第y年投资成本；为第y年第x个场景的运行费用；为第y年第x个场景的维护费用；为第y年第x个场景的停电损失费用；DR为折旧率；为第y年ESS 的容量；ICESS为ESS 单位投资费用；Dmax为柴油机组的最大数量为二进制值表示第y年i号柴油机组的购买状态；ICD为柴油机组单位投资费用；Wmax为风电机组的最大数量为二进制值表示第y年i号风电机组的购买状态；ICW为风电机组单位投资费用；OMCESS为ESS 的运行维护费用；ND为一年之中考虑的天数；(t)为场景x在t时刻的第i台柴油机功率；HR为消热率；FP为燃料费用；(t)为场景x在t时刻的第i台风机功率；OCW为风电机组的运行费用；为场景x下第y年的停电损失费用；VOLL为失负荷价值；LSx（t）为场景x下第t时刻的甩负荷量。

目标函数计算了现值中的所有成本，将（1+DR）-y与目标函数相乘可得到由于市场利率而产生的机会成本。

2.2 投资约束

由于经济和技术原因，投资约束如下所示：

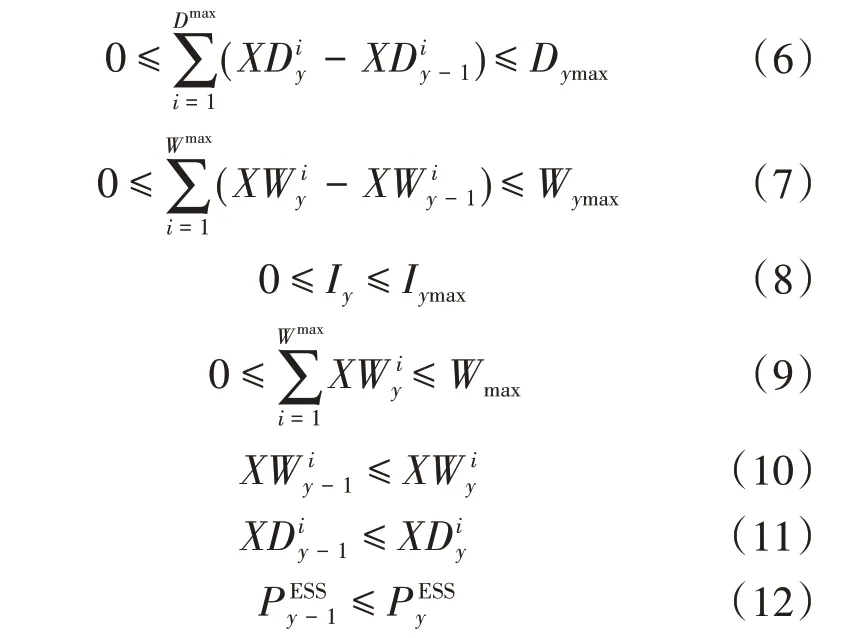
式中：Dymax为第y年允许的最大购置柴油机组数；Wymax为第y年允许的最大购置风电机组数；Iymax为第y年的最大投资；Wmax为允许的最大购置风电机组数。

2.3 运行约束

负荷或风力发电的干扰会导致瞬时功率平衡失配，因此需要对系统稳定性和扰动下的动态行为进行补充研究。

1）负荷平衡。第t时刻的总发电量和消耗量相等，即

3）柴油机组出力约束如下式所示：

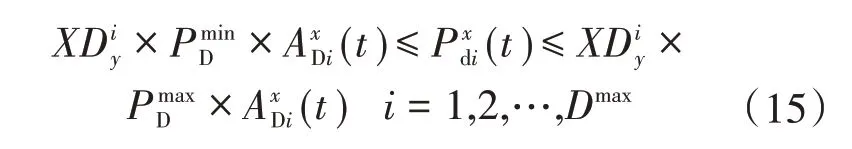
最小负荷、低负荷柴油技术和柴油机组是最常见的柴油机组运行策略。在模型中考虑到目标函数中的停电成本，隐含了旋转备用费用，因此对于每个柴油机组的旋转备用没有明确的限制。

2.4 ESS约束

2.4.1 功率约束和电量约束

功率约束和电量约束如下式所示：

式中：η为ESS效率。

2.4.2 电量日平衡约束

由于此规划模型中选择代表一年中4个季节的4天，各天之间没有连续性，一天的第一个小时和最后一小时在ESS中存储的电量必须相等，即

2.4.3 生命周期约束

随着时间的流逝，电池性能会下降，电池的储能能力会下降，这种现象称为电池容量衰减。电池生命周期的标准度量是电池容量减小到其标称容量的80%的时间[19-20]。因此，基于电池容量衰减的实际情况，相比于现有模型，本文新增考虑储能系统的生命周期约束。

电池容量吞吐量模型用于实现ESS生命周期估计。电池容量吞吐量表示在电池寿命耗尽之前可以通过的总A小时数或W小时数。为了确定电力系统中电池的预期寿命，传入或传出电池的W小时数是总和，当该值达到总吞吐量时，则认为电池寿命已用尽，如下式所示：此外，未考虑电池容量在其寿命终止之前因容量衰减而下降的影响（容量下降至其标称值的80%）。

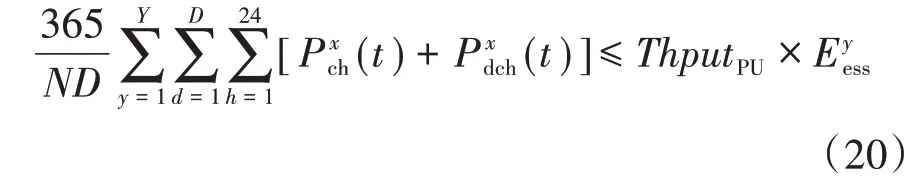
3 算例分析

3.1 系统概述

算例考虑了孤岛运行的风电-柴油机-储能系统，采用所提规划方法，使用遗传算法进行求解。该系统的基本负荷为120 kW，年增长率为8.0%。根据天气情况，一年中春夏秋冬的高峰负荷比例分别为0.81，1，0.87，0.92。

规划年限为10 a，起始年有3 个柴油机，功率分别为30 kW，40 kW 和50 kW，每个柴油机的平均能耗为8%，没有任何风力发电机组。一年中春夏秋冬形状系数I分别为1.23，1.09，1.35，1.42，比例系数值C分别为8.10，7.48，8.53，8.99。假设风电和柴油机类型均为一种，每台风电和柴油机的维护成本等于运行成本的2%，表1给出了柴油和风电机组的经济性能参数。

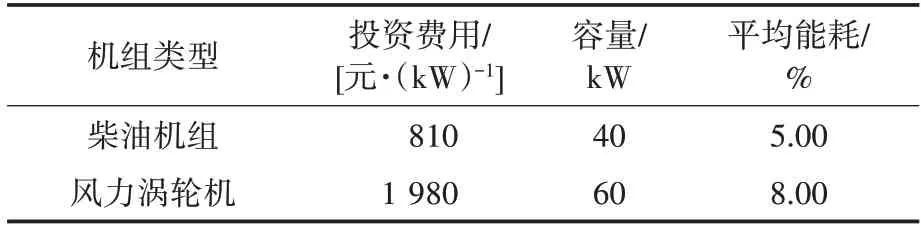
表1 发电机组数据Tab.1 Data of generator sets

考虑了3 种类型的电池作为不同的ESS。类型1 是典型的钠硫电池，类型2 代表了一种低成本的铅酸电池，类型3 是典型的溴化锌。表2 列出了候选电池的技术和经济特性参数取值。

表2 ESS数据Tab.2 Data of ESS

为简单起见，假设DoDmax=1，DoDmin=0。生成的场景的初始数量是100，每个场景发生的概率均为1%，使用GAMS/SCENRED 快速倒推法可以将场景数减少为6，从其余场景获得的失负荷时间期望的最大允许标准偏差假定为0.01。表3 列出每个最终场景的概率。

表3 削减后各场景概率Tab.3 Probability of scenarios after reduction

3.2 效率分析

所有方案中折现率为12%，燃油价格为11.25元/L，热费率为24（kW·h）/L，VOLL为37.5 元/（kW·h），LOLEfix为失负荷时间期望固定值，h/阶段。为了说明该方法的高效性，分析了以下3类扩展规划方案，其规划期限为10 a：

方案A：没有ESS；

方案B：在规划初始年以最佳容量装备ESS，ESS仅考虑类型1；

方案C：ESS分别考虑了3种类型。

假设ESS 的电量功率比为1.2。由于技术限制和站点位置的地理条件，一年中要安装的风力涡轮机的数量限制为2，规划时间范围内的风力涡轮机的总数限制为8。

规划结果如表4 所示，方案A 的总成本为156.38 万元/a；在方案B 中采用电池类型1 作为ESS可将总成本较方案A降低3.62%；通过使用类似电池类型，方案C1中的成本降低为12.89%。此外，随着风电机组的规模的增大，方案C1的ESS容量扩展规划较方案B更优。在限制了风力发电机组的总数条件下，小型风力发电机组中不可能达到最佳的风力渗透率，系统总成本会增加。

根据表4，方案C1，方案C2和方案C3的总成本降低分别为12.87%，2.45%和10.12%。尽管类型1的电池价格高昂，但由于其效率和循环寿命较高，使其利润更高。相反投资成本和循环寿命更低的类型2对能源管理效果有限，在容量扩展规划中，ESS的运行参数以及经济参数都具有更为重要的作用。因此，考虑了ESS 充放电次数的建模效率和循环寿命的能力是所提方法的主要优点之一。

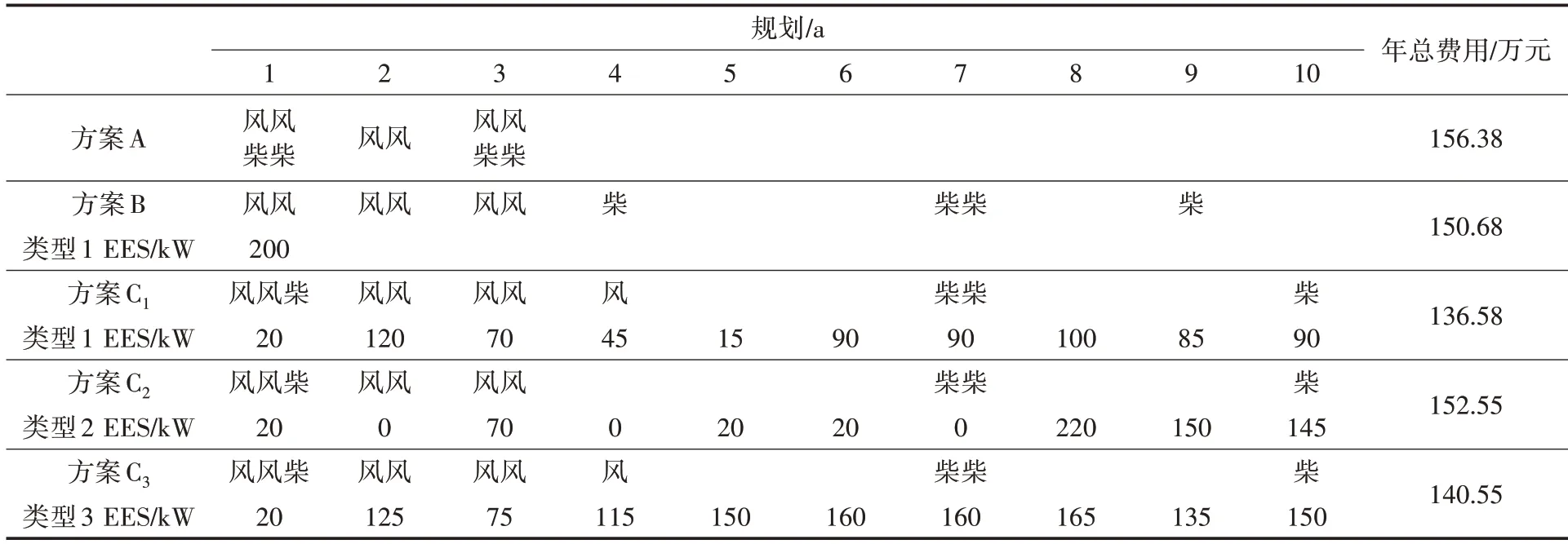
表4 规划年间风电及柴油机组容量扩展规划方案及费用Tab.4 Capacity expansion plans and costs of wind power and diesel units during the planning period

图1 给出了风力发电机组的大小为40 kW 的情况下，生命周期和AC/AC 转换效率对ESS 在规划中占比的影响。可以看出，使用周期越长，AC/AC 转换效率越高，ESS 带来的经济效益越好，在容量扩展规划中的占比越高。

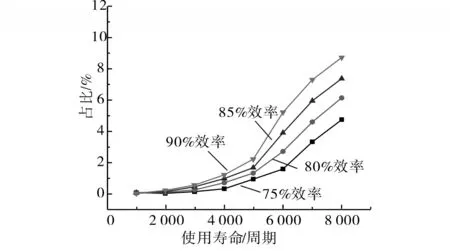
图1 生命周期和效率对ESS影响Fig.1 Influence of service life and efficiency on ESS

3.3 灵敏度分析

ESS 的电量功率比是ESS 应用中的重要参数，不同的电量功率比适用于不同的ESS。图2显示了在3 种不同的规划方法中，从ESS 安装获得的利润的灵敏度分析。当电量功率比分别为0.4，1.2和0.8时，可获得类型1、类型2和类型3的最大利润。风力发电机组的尺寸是总成本中的重要参数，但柴油机组的尺寸并不是一个很重要的参数。图3则给出了在不同方案中LOLEfix的更改对总成本的影响，如果将失负荷时间期望修复设置为更高值，由于削减负荷能力的提高将使得总成本降低。

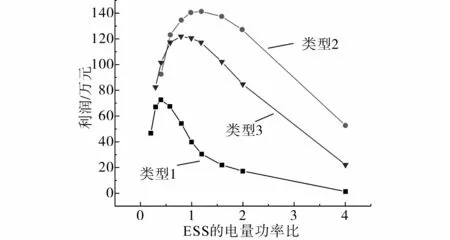
图2 ESS电量功率比影响Fig.2 Influence of ESS power ratio

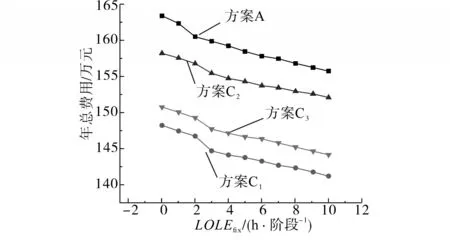
图3 LOLEfix取值影响Fig.3 Influence of LOLEfix value

柴油机的运行成本是燃油价格的直接函数，因燃料价格影响柴油和风电机组的能源供应贡献以及能源交易总量。燃料成本的增加导致风力单元渗透率的增加，因此风电的随机性将导致ESS的能源交易量增加，如图4所示。

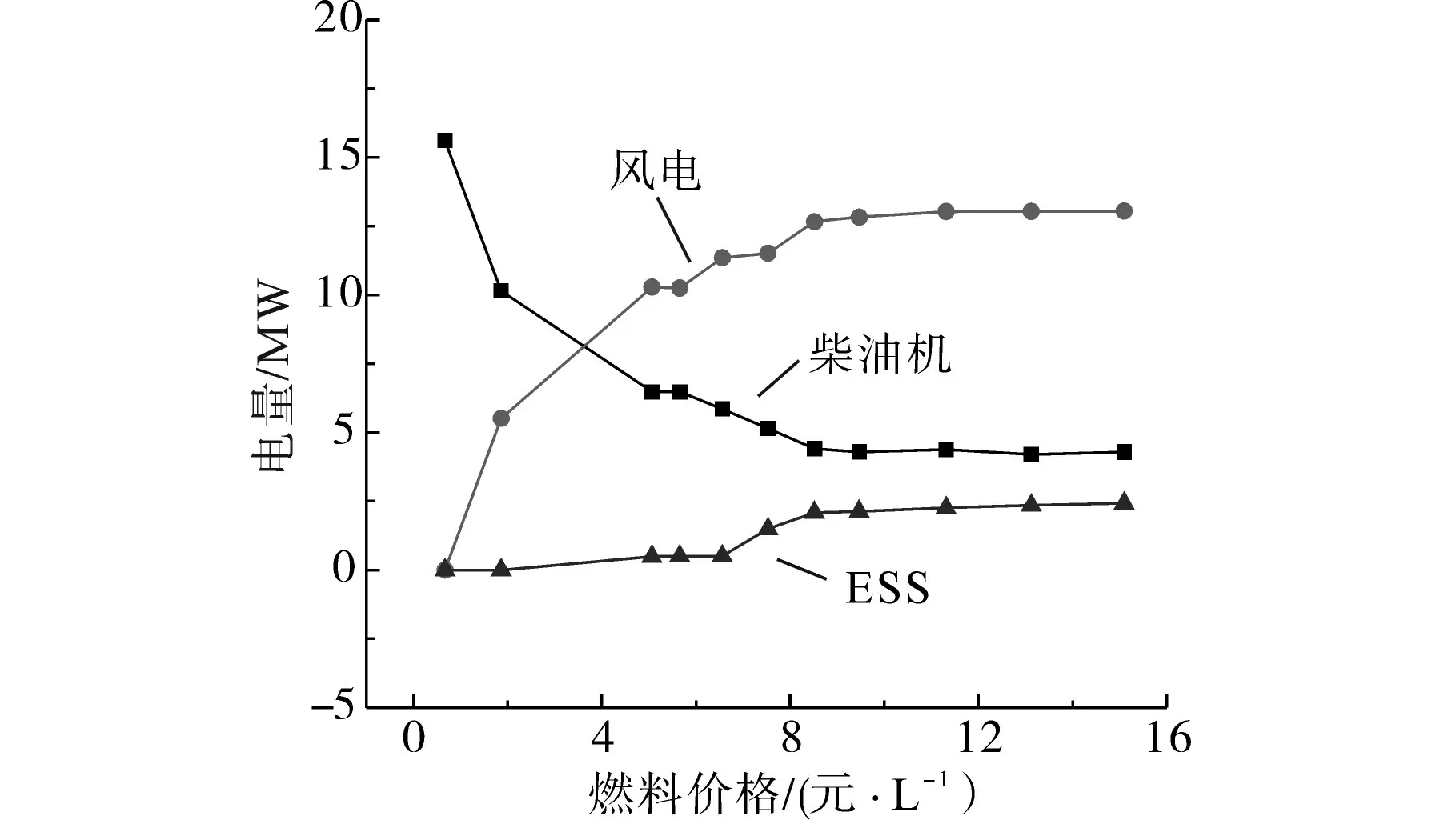
图4 燃料价格影响Fig.4 Influence of fuel prices

4 结论

本文使用基于蒙特卡洛方法的随机规划方法来处理问题中的不确定性，并且在风电-柴油机-储能组合电力系统的容量扩展规划中采用了一种新的方法来模拟能源服务系统的运行约束。将所得到的结果与传统ESS 初始规模进行了比较，结果表明在扩容过程中可节省10%的成本。由算例分析可知在容量扩展规划中，ESS 的运行参数与经济参数同等重要，两类参数的显著变化均会影响ESS技术的选择。

总的来说，该方法的优点是能够在较长的时间范围内扩展ESS，从而降低成本。应注意的是，在实践中，ESS扩展可能会引入一些隐藏的成本，如与施工设备运输相关的成本、当地许可要求以及每次系统升级时所需的任何电力系统研究。