NPC三电平变换器电流谐波最优PWM策略

朱燕，陈进

（1.国网重庆市区供电公司，重庆 400015；2.国网重庆市电力公司，重庆 400015）

中点钳位型（neutral-point-clamped，NPC）三电平变换器广泛应用于风电和牵引等工业领域，其与两电平拓扑相比优势在于输出电压谐波含量低和功率开关器件额定电压低等[1-2]。

NPC 三电平变换器的脉宽调制（pulse width modulation，PWM）策略较多，如SPWM，SVPWM和方波调制等[3]。为了降低NPC 三电平变换器开关损耗，学者们提出了一些低开关频率PWM 方法，如不连续脉宽调制[4]和特定谐波消除脉宽调制[5]（selected harmonic elimination pulse width modulation，SHEPWM）等。其中不连续脉宽调制通过事先弃用SVPWM 中的一些基本电压矢量来减小共模电压，并优化钳位模式来实现中点电位（neutral-point potential，NPP）平衡，属于一种混合调制策略，相比常规调制的开关频率有所减少，但较之SHEPWM，开关损耗仍较大，且计算量较大。SHEPWM 可以根据谐波要求求解SHEPWM波形的傅里叶方程来对特定低次谐波进行消除，但NPP 控制将变得困难。NPP 不平衡可由空载、不对称负载和系统不一致性等引起，严重时可引起开关器件过压击穿和直流侧电容过压损毁[6]。故文献[7-9]中根据谐波优化目标，离线计算后优化SHEPWM以实现中点电位平衡，但存在SHEPWM波形偏离和NPP 控制折衷问题。文献[10]采用了三级滞环控制器，以期在开关角求解后进行冗余矢量调整，完成实时中点电位控制，但该方法对于低频NPP脉动也是效果欠佳的。

由前述文献研究，本文提出了一种针对NPP低频脉动抑制的电流谐波最优PWM策略。首先，对引起NPP 低频脉动的根本原因进行分析，然后找出最优3次和9次谐波分量，可自然地实现NPP低频脉动最小，而无需在线更改任何开关角。然而，由于所提出的方法牺牲了两个开关角以确保最优3次和9次谐波分量，这意味着将只有更少的开关角可用于消除其他低次谐波。因此，将最优3次和9次谐波分量和THD联合来定义目标函数进行求解，可兼顾实现最小电流谐波和NPP脉动最小。

1 SHEPWM的NPP问题分析

1.1 三电平SHEPWM 方案

SHEPWM 的基本原理是根据谐波要求计算PWM 波形的开关角，以消除特定低次谐波，以u相位为例，SHEPWM 输出波形如图1 所示，开关角为α1，α2，…，αn。

对图1中SHEPWM波形进行傅里叶分解可得：

式中：udc为直流侧电压；an，bn为傅里叶系数；ω为基频；N为1/4周期内开关角个数。

设基频分量为u1，调制比m=u1/（2udc/π），则SHEPWM 设计时令基频分量|a1|=m，其他低次谐波分量|ah|=0，如下所示：

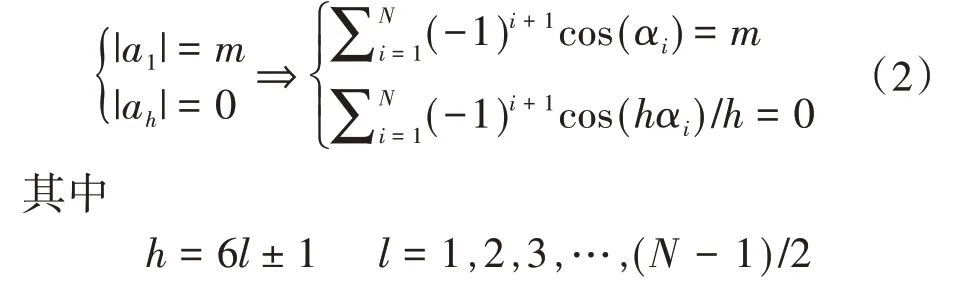
式中：h为谐波次数。

根据所设计目标函数，对式（2）所描述非线性方程进行数值求解[11]，可得最优开关角，其中目标函数定义为

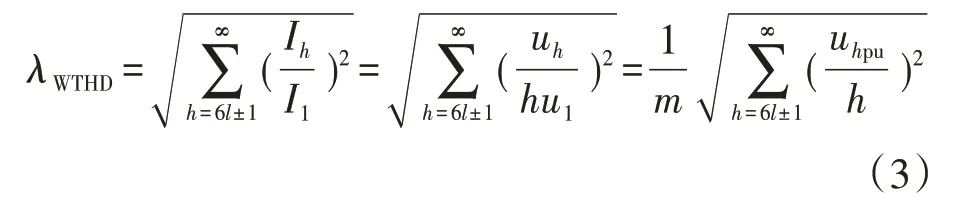
式中：λWTHD为目标函数；Ih，uh分别为谐波电流和电压；I1为电流基频分量；uhpu为谐波电压的标幺值。

1.2 NPP问题及其传统解决方案

忽略谐波分量后的NPC 三电平变换器三相电压和电流表达式分别为

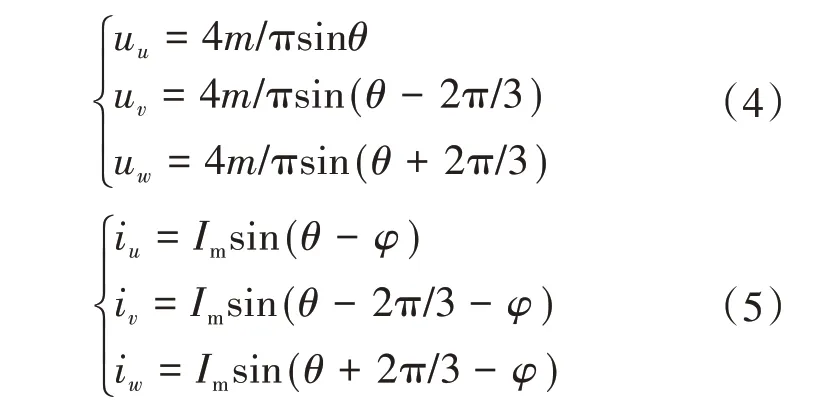
式中：Im为基频电流幅值；φ为相角。

中性点电流io可表示为

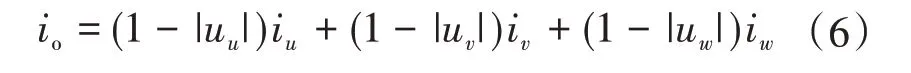
式（6）表明，io由相电压和电流决定，而死区或不对称负载将使式（4）～式（6）中的电压或电流正弦度不好，从而出现NPP 偏移问题。故需要对NPP施加控制。如前所述，由于计算复杂，可采用离线计算得到谐波需求对应的开关角，然后通过改变开关角来应对NPP偏移问题[7-9]，如图2所示。

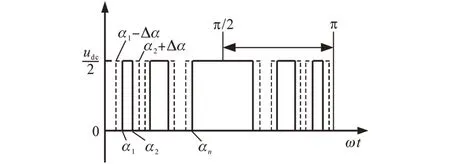
图2 考虑NPP控制的SHEPWM波形Fig.2 SHEPWM waveform when considering NPP control

从图2 中可看出，通过变量Δα调整开关角，NPP 可得到修正。但Δα对于该方法的性能至关重要，如果Δα太小，则控制能力较弱，反之则会使得输出性能变差，故Δα的选择需进行折衷考虑。综上，离线优化计算方法存在一定的局限性。

2 新型电流谐波最优PWM方案

根据前述SHEPWM及其NPP控制原理，可知谐波性能是由开关角决定的。但NPP 控制角是根据谐波要求离线计算的。因此，在计算这些角度之前，必须考虑NPP 低频脉动，本文对NPP 低频脉动对应的最优开关角进行了求解。

传统SHEPWM 根据式（2）来获得开关角，以消除所选的低次谐波分量。式（2）没有考虑3n次谐波分量，因为其对三相三线制系统的线电压没有影响。但本文将3n次谐波分量加入分析，如下式所示：

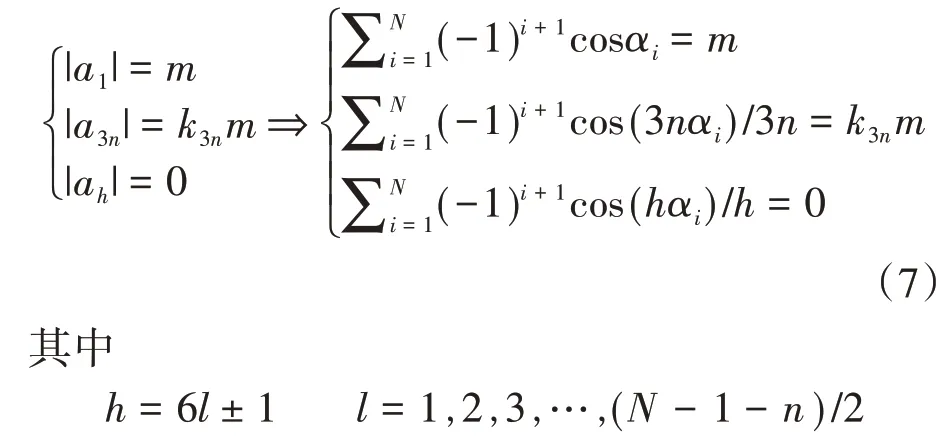
式中：k3n为3次谐波分量的幅值。为了实现NPP低频脉动最小，对应3n次谐波分量将存在最优值以抵消基频分量引起的NPP 低频脉动。

2.1 io与3次谐波分量间的关系

3次谐波分量的表达式为

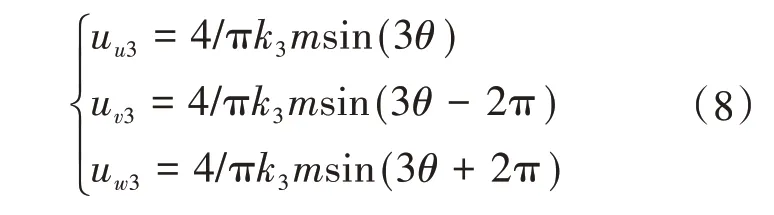
将式（4）、式（5）和式（8）代入式（6），可重写io为

式（9）表明，可通过k3来调节io，当NPP 低频脉动最小时，k3为最优，但很难直接从中得到k3的最优值。式（9）中，若k3改变了式中绝对值符号，则简化io和k3之间的关系变得困难，故先确定不改变绝对值符号的k3的范围为-1/3＜k3＜1，当k3最优值在此范围内时，由于绝对值符号不变，可得io和k3之间的关系式为

其中

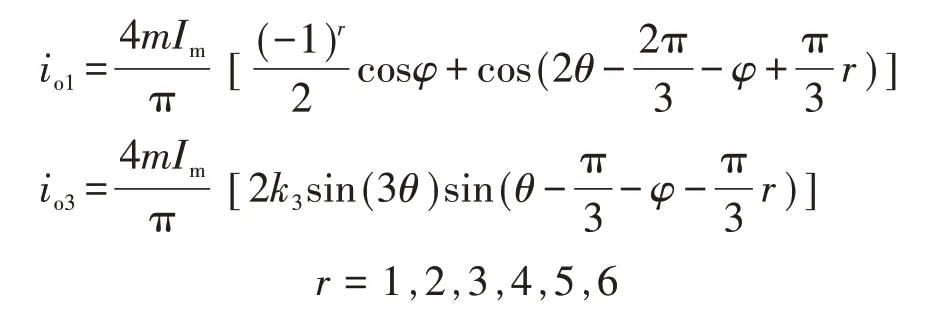
式中：io1为由基波电压产生的中性点电流；io3为从3次谐波电压得出的中性点电流。io1和io3的频率均比基频大3倍。

图3显示了在不同功率因数（power factor，PF）下io，io1和io3的波形。从图中可看出，io3总体上与io1相位相反，特别是当PF增大时。因此，若合理设置io3的值，则io1可被抵消，从而优化NPP低频脉动。

图3 不同PF下io，io1和io3的波形Fig.3 Waveforms of the io，io1 and io3 with different PF

设s(io1)和s(io3)分别为io1和io3的积分值，令s(io1)=-s(io3)，则k3最优值可按下式获得：

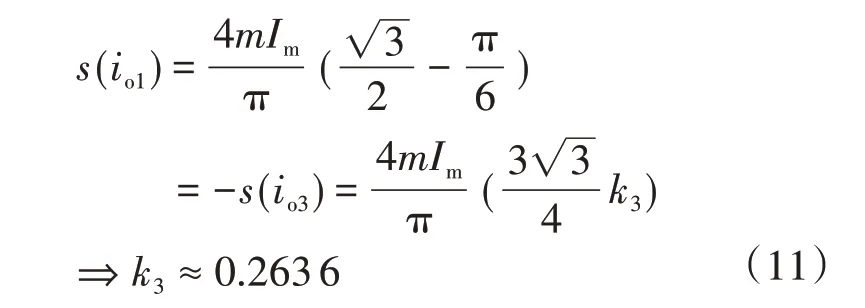
进一步，对通过式（11）中io，io1和io3积分可得不同PF下uo，uo1和uo3的规律。此外，定义NPP 低频脉动抑制系数gsc=uok326/uok30，其中uok326和uok30分别是当k3=0.263 6 和k3=0 时NPP 波动的最大值，计算显示当PF增加，尤其是当PF＞0.6 时，gsc显著减小，NPP 低频脉动将被抑制。另一方面，由于不能确保所有PF下io3与io1反相，故当PF较小时，NPP低频脉动抑制效果不明显。因此，当NPC三相变换器带电机类负载时，PF通常大于0.6，故此方案非常适合于大多数电机驱动系统。

2.2 io与9次谐波分量间的关系

与传统SHEPWM方案相比，应用3次谐波分量将可能导致更大的9 次谐波分量，对NPP 也有一定的影响，需进行分析。类似于k3求解，为了不改变式（6）中绝对值符号，k9必须满足-1/9＜k9＜1/2。因此，推导可得io和k9之间的关系如下式：

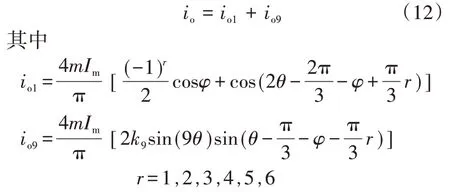
图4 为不同PF下io，io1和io9的波形，其中io9是基于9 次谐波电压得到的中性点电流，k9仍设置为0.263 6。可观察到，io9的频率是io1的3 倍，io1和io9间的相角差只能调整为0 或π，故无论如何设置k9，都难以利用io9来抵消io1。同时，图4 表明，较大的k9值会使io波形恶化，故只能将k9设置为接近0，以抑制源自io9的NPP低频脉动。

图4 不同PF下io，io1和io9的波形Fig.4 Waveforms of the io，io1 and io9 with different PF

2.3 最优开关角计算

对于传统SHEPWM 方案，需牺牲2 个开关角以实现NPP 低频脉动最小，故可用于消除其他低次谐波的开关角非常少。而使用所设计的电流谐波最优PWM 代替SHEPWM 可同时实现谐波电流最小和NPP 低频脉动抑制。新的谐波要求如下所示：

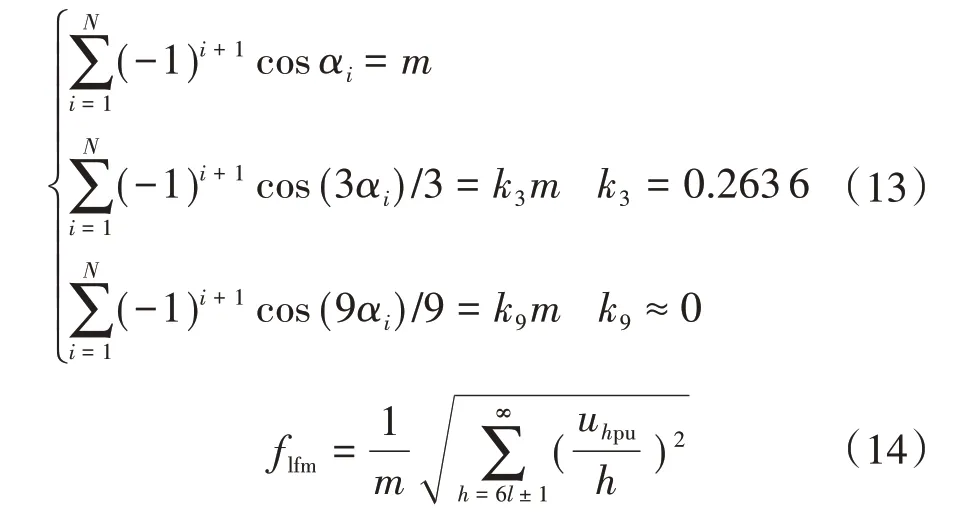
式中：flfm为总电压谐波含量；uhpu为各次谐波电压标幺值。

因为式（13）和式（14）与传统方案要求不同，因此开关角的计算非常容易，且相对于传统方案收敛性更好。

值得注意的是，flfm必须在允许范围内。如果k3和k9取值不合理，则可能得不到有效解。故开关角、迭代初值和算法收敛性均与传统SHEPWM方案不同，下面将进行详述。

3 新方案与传统SHEPWM对比

尽管已获得了k3和k9的最优值，但使用k3和k9的最优值来计算开关角时，有一个与m相关的求解范围，当m较大时可能无解。为了细化分析，后续对比中将电流谐波最优PWM 策略分为两种，一种是只考虑3次谐波电流的方案，还有一种是考虑3 次和9 次谐波电流的方案。当N=1时，三种调制都变为方波调制，m最大均可达到1。当N=2 或N=3，以及N＞4 且为奇数时，SHEPWM的m最大均可达到0.9，但当N＞4 且为偶数时，SHEPWM 的m最大只有0.5。对于两种电流谐波最优PWM 策略而言，当N＜3 时，是没有有效解的，因为已使用了两个开关角来控制3 次和9 次谐波分量，故没有开关角来控制基频分量。因此，仅当N＞4 时，才可使用这两种方案，但无论N为奇数还是偶数，m最大均可以达到0.9，故这一点是优于传统SHEPWM方案的。

如前所述，若基于式（13）和式（14）的谐波要求来计算开关角，则可实现NPP 低频脉动最小化。但这也意味着需要牺牲一定的自由度来控制3 次和9 次谐波分量，从而降低NPC 三电平变换器的输出性能，故下面对传统SHEPWM 方案和两种电流谐波最优PWM 方案的λWTHD进行了比较，结果如图5所示。

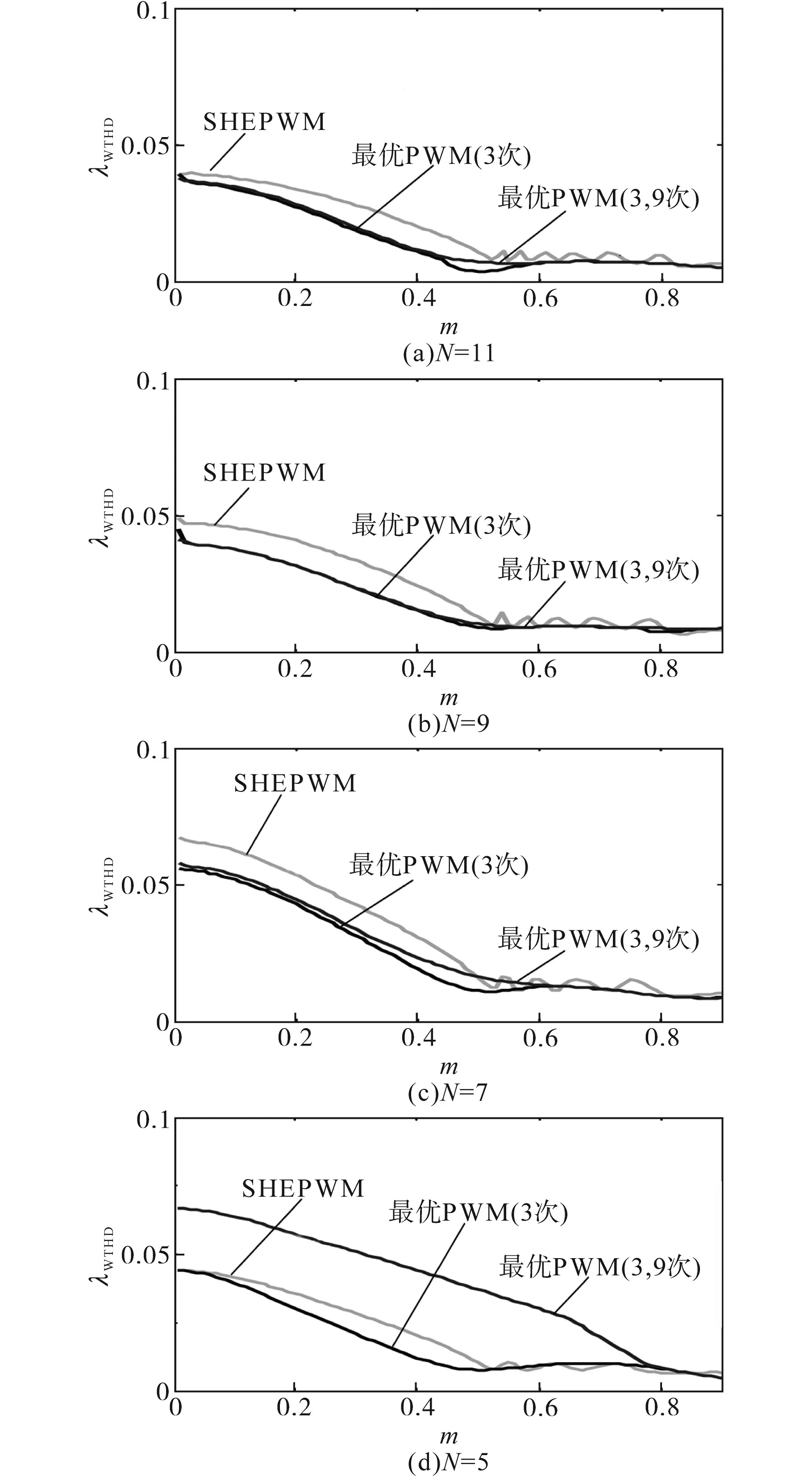
图5 不同方案下的λWTHD对比Fig.5 Comparisons on λWTHD of the different schemes

考虑当N为奇数时，可在较大线性调制区内求解SHEPWM 的开关角，故考虑在N为奇数时，对比各方案的输出性能。从图5 可以看出，只考虑3 次谐波电流的最优PWM 方案在不同N取值时具有最好的输出性能，即不同调制比m下λWTHD均最小，但由于不处理9次谐波，故NPP低频脉动抑制能力不如考虑3 次和9 次谐波电流的最优PWM 方案。此外，当N＞5时，两种最优PWM 方案的输出性能都显著优于传统SHEPWM 方案。但当N=5 时，考虑3 次和9 次谐波电流的最优PWM方案的输出性能会明显下降，因为可用于改善谐波的自由度非常少。不过若m＞0.8，即使N=5 或4，各方案的输出性能也是相似的，这对于电机驱动应用场景非常重要，因为输出频率通常与m成正比，故仅当m较大时才选择较小的N以减小开关频率。

4 实验验证及结论

为验证所提出最优PWM 方案的效果，搭建了小功率样机以进行实验研究。其中变换器的控制系统基于DSP（TMS320C6657）和FPGA（XC6SLX45）实现，前端供电由电网通过滑动变压器和不控整流器提供，设置直流母线电压udc=220 V，NPC 三电平变换器直流侧上、下电容Cup=Cdown=1 800µF，开关频率fsw=245 Hz，死区时间tde=4µs，负载电阻Rload=10 Ω，负载电感Lload=5 mH。

图6和图7分别为传统SHEPWM 方案和考虑3 次谐波电流的最优PWM 方案的实验结果，测试中设置N=7 和m=0.6。从图6c 中uu波形FFT 分析可看出，传统SHEPWM 方案下3 次谐波分量幅值约为0.38，且与基波分量的相角差为π，假设基频分量k1为1，则3 次谐波分量k3=-0.38。对比图7c可发现，3 次谐波分量与基波分量的相角差为0，且3次谐波分量k3=0.263 6。因此，传统SHEPWM生成的k3将导致较大的NPP 低频脉动，Δuo振幅达到±3.8V，Δuo的FFT 分析见图6d，其中NPP 低频脉动频率为3 倍频，这印证了前述理论分析。从图6c 和图6d 可看出，所选的5 次、7 次、11 次、13 次、17 次和19 次电压谐波分量已完全消除。对于考虑3 次谐波电流的最优PWM 方案，已将3次谐波分量从k3=-0.38 改为最优值k3=0.263 6。这使得NPP 低频脉动抑制为±1.5V，见图7b。通过对Δuo进行FFT 分析可知，NPP 低频脉动的频率集中为9 倍频和15 倍频，这源自9 次和15 次电压谐波分量，但NPP 的3 次谐波分量已得到明显改善。

另一方面，对比图6c 和图7c 可看出，SHEP⁃WM 方案和考虑3 次谐波电流的最优PWM 方案下的相电压THD 分别为61.50%和87.01%，但系统为三相三线制，故线电压会自动消除3n次谐波分量，即线电压THD 分别为37.89%和36.17%，对应相电流THD分别为13%和11.59%，均是SHEP⁃WM 方案略高。因此，即使新方案使用了一个开关角来抑制NPP 低频脉动，也不会导致输出性能下降，验证了其是一种兼顾控制NPP 低频脉动和输出性能的较好方案。

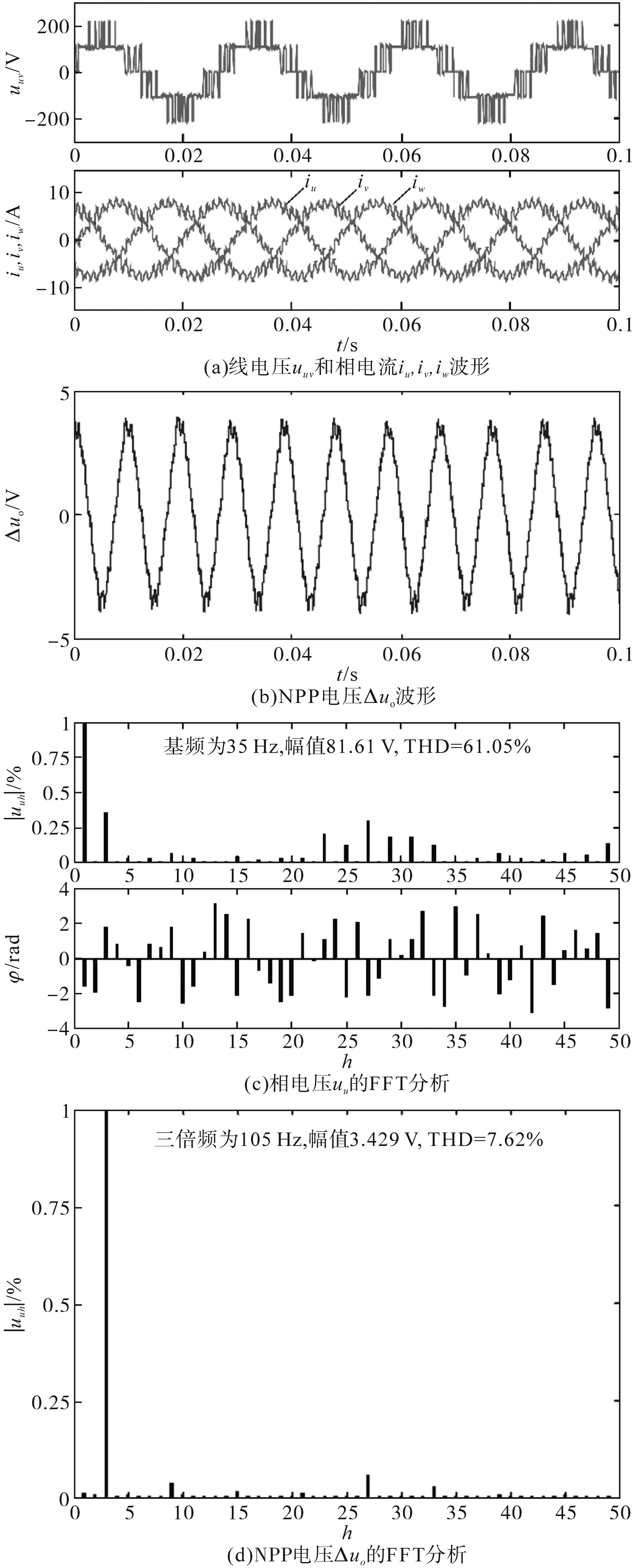
图6 传统SHEPWM的实验结果Fig.6 Experimental results of conventional SHEPWM scheme

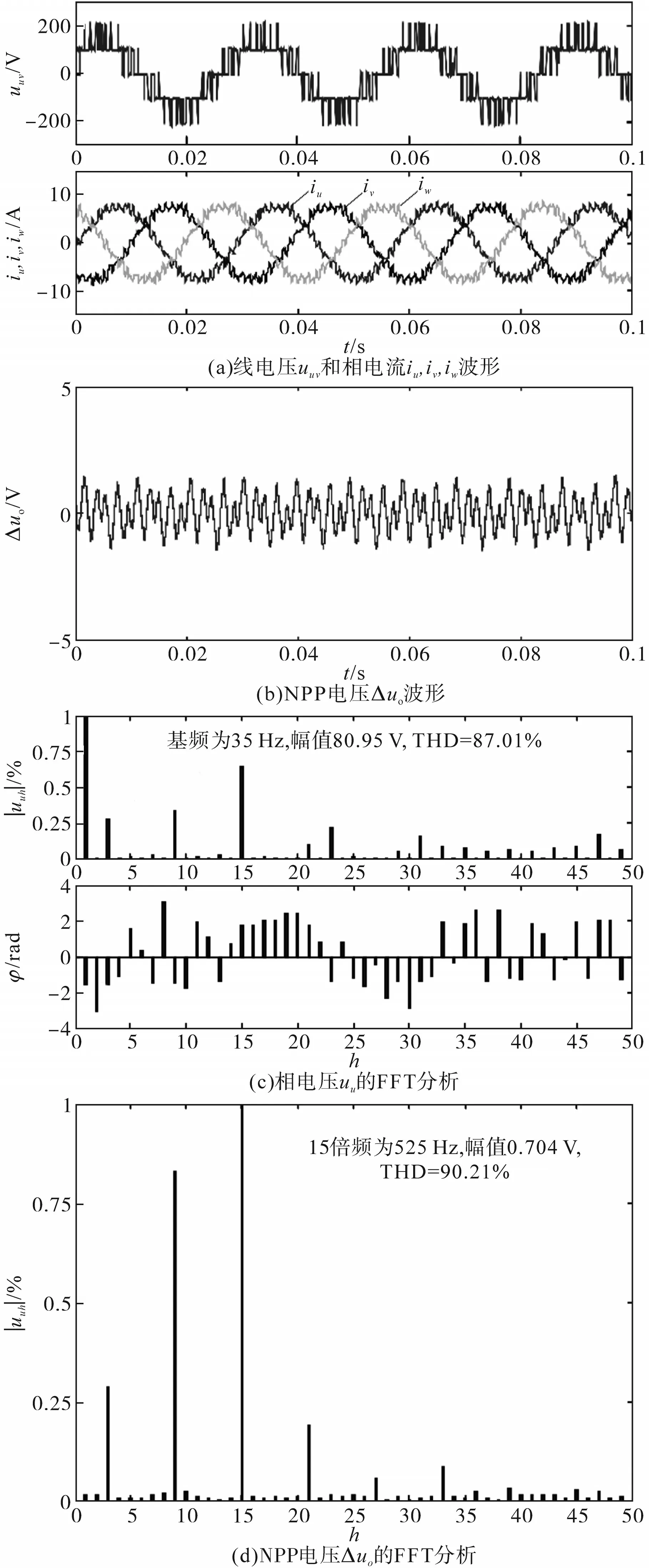
图7 新型最优PWM（考虑3次谐波）的实验结果Fig.7 Experimental results of novel optimal PWM scheme（considering 3rd harmonic）

本文针对NPC 三电平变换器的NPP 低频脉动问题，提出了一种新型谐波电流最优PWM 方案，总结全文可得出以下结论：

1）传统SHEPWM 方案中存在的NPP 低频脉动问题非常难处理，因为其没有更多的自由度在线控制NPP；

2）由于NPP 低频脉动由SHEPWM 的基频分量和3n次谐波分量形成，故电流谐波最优PWM策略优化了3次和9次谐波分量，在减少2个可变开关角的情况下仍可显著抑制NPP 低频脉动，实验结果验证了其输出性能仍较优，因而为解决NPP 低频脉动问题并同时保持良好的输出性能提供了一种新途径。

进一步的研究方向是推导NPP 低频脉动与傅里叶分解式中的相角之间的数学关系，以探明电流谐波最优PWM策略性能边界和实用效果。