开关电感级联型高倍升压AC-DC变换器

李咏秋，杨喜军

（上海交通大学电力传输与功率变换控制教育部重点实验室，上海 200240）

单相二极管整流桥后置非隔离升压型DCDC 变换器，可构成单相功率因数校正器，其中升压电感的工作模式包括连续导电模式（continu⁃ous conduction mode，CCM）、临界导电模式（criti⁃cal conduction mode，CRM）和断续导电模式（dis⁃continuous conduction mode，DCM）。鉴于传统升压型DC-DC 变换器的升压能力一般不大于4～5倍，交流电压源供电的有桥型或无桥型单相功率因数校正器[1-3]的升压能力一般为网压峰值的1～2倍，否则占空比过大会影响升压变换器的稳定性和可控性。某些需要高压的应用场合，如X 射线医疗或工业、高压装置绝缘测试、静电除尘等，需要二次升压变换，因此存在电路结构复杂和整机效率较低等实际问题。

非隔离升压型DC-DC 变换器包括传统两电平、三电平以及高倍升压型等多种构成方式，高倍升压型DC-DC 变换器又包括开关电感型[4-5]、开关电容型[6-8]以及级联升压型[9-11]等多种构成方式，具有很强的升压能力。基于高倍升压型ACDC 变换器的单相功率因数校正器，在输入低压时可以获得高压直流输出，同时获得网侧较高功率因数，功率开关可工作在较低占空比而不会造成控制不稳。

本文继续对文献[4-5]给出的开关电感型高倍升压变换器进行跟踪研究，根据其工作原理为升压电感处于并联充电、串联放电状态并结合级联升压型变换器的结构特点，提出一种新型开关电感级联型高倍升压AC-DC变换器，级联数不受限制。采用单周期模拟控制器IR1155S控制并进行关键参数计算，最后进行仿真与实验验证。

1 高倍升压电路工作原理

1.1 功率电路分析

由文献[4]，可以得到一种开关电感型高倍升压AC-DC 变换器，如图1a 所示。该电路的特点是：升压电感数量为2 个，可控功率开关数量为1个，功率二极管数量为4 个，且D5，D6与D8为反向快速恢复型，整流桥与输出电压共地，驱动器与驱动电源数量均为1 个，可以采用现有模拟控制器。现有模拟控制器带有非隔离驱动器，支持较高的开关频率，无需隔离电量检测。功率二极管D7可以为反向慢速恢复型二极管。

文献[5]给出了一种开关电感型高倍升压AC-DC 变换器，如图1b 所示。该电路的特点是：升压电感数量为2 个，可控功率开关数量为2 个，功率二极管数量为1个且为反向快速恢复型二极管，整流桥与输出电压异地，驱动器与驱动电源数量均为2个，可采用数字控制器，需要额外高速隔离驱动器，需要隔离电量检测。

图1 文献[4-5]得到的开关电感级联型高倍升压AC-DC变换器Fig.1 Switched inductor based high transfer-ratio Boost AC-DC converters obtained from reference[4-5]

图1 所示电路结构比较简单和易于实现，但是不具备级联结构，均不能推导出更高倍升压结构，且图1b所示电路在电感量不等而两个开关同时开断时，会产生超高浪涌电压。利用升压电感并联充电和串联放电升压的基本原理，本文提出如图2 所示的高倍升压单相AC-DC 变换器，图中给出了三级升压结构，理论上只有最后一级结构中的功率二极管D9和D10需要采用反向快速恢复型二极管。

图2 开关电感级联型高倍升压AC-DC变换器Fig.2 Switched inductor multi-cascaded high transfer-ratio Boost AC-DC converter

1.2 升压原理分析

1.2.1 感量相等

在图2 中，当功率开关S1～S3导通时，二极管D5，D7压降较小，功率开关S1～S3的导通压降相近，因此升压电感L1～L3端电压近似相等，并联充电，升压电感电流上升斜率为

式中：ui为输入电压。

电感电流上升斜率取决于网压瞬时值和感量大小。当功率开关S1～S3断开时，若感量相等则每个电感电流瞬时值相等，电感串联放电，所有升压电感电流下降斜率为

式中：uo为输出电压。

升压电感可以工作在CCM 或CRM 下，在相同驱动脉冲作用下，起始放电电流相等，放电用时相同，则各电感电流谷值相同。在这种情况下，当级联数为N时，电压变比为

式中：d为开关器件控制脉冲占空比。

由此可见，随着级联数N与占比增加，升压能力增强，如图3 所示。图4 中给出了感量相等时CCM 下，采用相同的驱动脉冲，该AC-DC 变换器的有关波形。

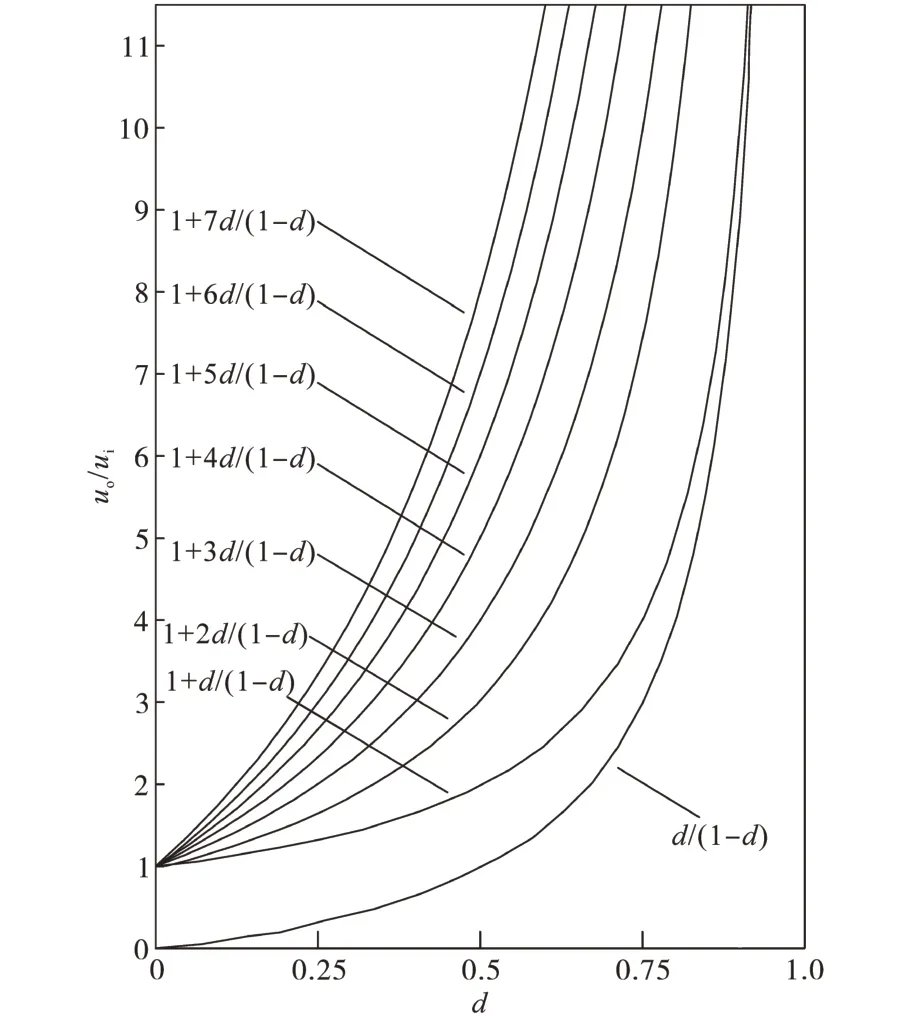
图3 感量相等时CCM模式下变换器电压变比波形Fig.3 Voltage transfer-ratio waveforms of the AC-DC converter with equal inductances in CCM

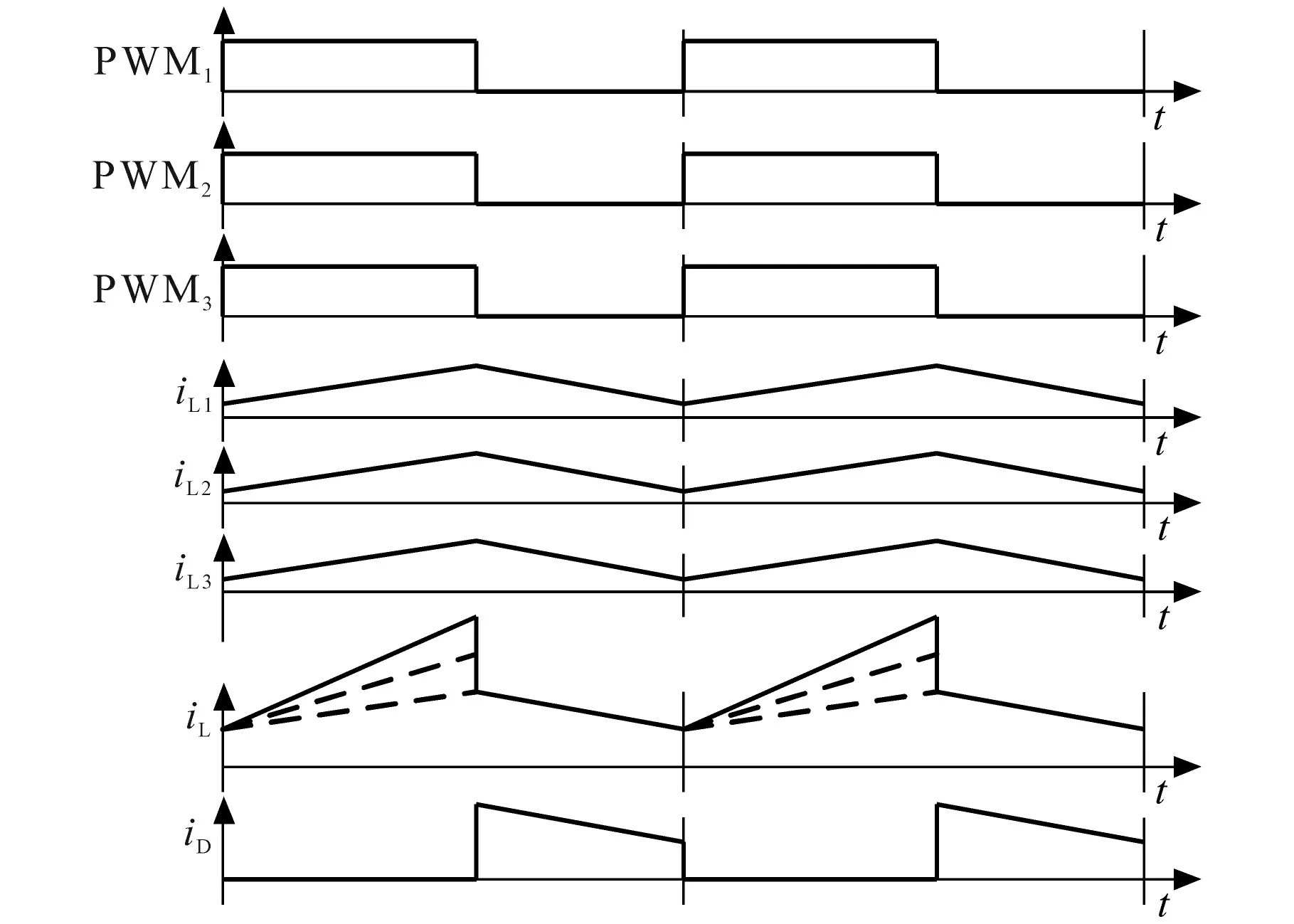
图4 感量相等时CCM下有关波形Fig.4 Waveforms of the proposed AC-DC converter with equal inductances in CCM

1.2.2 感量不等

电感感量不等且功率开关S1～S3同时断开时，由于升压电感电流上升斜率不等而充电时间相同，故而功率开关断开瞬间，三个升压电感电流不等。不失一般性，设L1＞L2＞L3，则功率开关关断瞬间，iL1最小、iL3最大。忽略功率二极管及功率开关压降，功率开关S1～S3断开后的续流阶段包括三个阶段：

阶段1：L1与L2电流基本不变，L3电流下降，电流下降斜率为(|ui|-uo)/L3，输出电流iD等于L3电流，斜率较大。后级电解电容充电电压为|ui|+L3diL3/dt；

阶段2：L1电流基本不变，L2，L3串联续流，电流下降斜率为(|ui|-uo)/(L2+L3)。后级电解电容充电电压为|ui|+(L2diL2+L3diL3)/dt；

阶段3：L1，L2与L3串联续流，电流下降斜率为(|ui|-uo)/(L1+L2+L3)。后级电解电容充电电压为|ui|+(L1diL1+L2diL2+L3diL3)/dt。

出现上述三个阶段的原因如下：阶段1 电感L1，L2分别与二极管D5，D7并联后与L3串联续流。由于二极管D5，D7的导通，造成大电感端电压钳位至零，使得电感电流出现近似恒流区；当iL3下降至与iL2相等时，流经D7电流下降至零，D7自然关断，L2，L3串联续流，进入阶段2；同理，当iL2下降至与iL1相等时，流经D5电流下降至零，D5自然关断，进入阶段3。

因此，感量不等时电感电流不会突变，不会因电感电流突变产生超高浪涌电压危害器件安全。在感量差别不大时，三个电感将尽快进入阶段3，电感电流的谷值将始终相等，谷值不为零时，即可工作在CCM下。

图5 给出了感量不等时CCM 下，采用相同的驱动脉冲，该AC-DC变换器的有关波形。

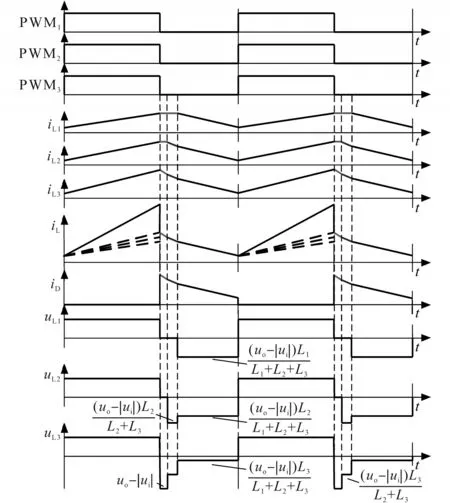
图5 感量不等时CCM下有关波形Fig.5 Waveforms of the proposed AC-DC converter with unequal inductances in CCM

综合以上分析，相比图1，图2 所示电路具有如下特点：

1）具有可以扩充的、更高的升压能力，感量相等或不等时都可以工作在CCM下；

2）可以采用现有的APFC 模拟控制器，如L4981BD，UCC3854，IR1155S等，所有功率开关可以采用同一驱动器或独立采用驱动器；

3）功率地、控制地与检测地共地，节省检测电路成本；

4）对于N级升压结构，高端只需采用N个二合一的共阴极功率二极管。

2 单周期控制器设计

图2 所示的高倍升压AC-DC 变换器可以采用现有模拟控制器、数字控制器实现。数字控制器适用于升压电感工作于CCM 或DCM 情况，但是现有模拟控制器只适用于升压电感工作于CCM情况。

本文选取单周期控制（OCC）原理和CCM 控制模式的模拟控制芯片IR1155S 作为控制器，设计如图6 所示的高倍升压单相AC-DC 变换器。考虑到该电路控制地、功率地、检测地相同，且非隔离型驱动器延时小、驱动电流大，图中选用非隔离型驱动器FAN3100 作为功率开关驱动器。

为有效控制漳州核电工程前期费用、提高资金使用率、降低项目建设成本，根据项目前期工作实际进展及FCD 前工作计划，前期投资以不超过投资估算总资金的10%为原则进行控制，综合研判FCD前工作量，签订可量化的FCD前工作协议，通过工程量核算方式减少前期费用投入约3亿元。其次建立支付、变更管理台账，对项目管理费、设计费、设备费、建安费进行从严从紧控制并与兄弟核电厂对标参考，优化完善FCD前支付控制曲线。

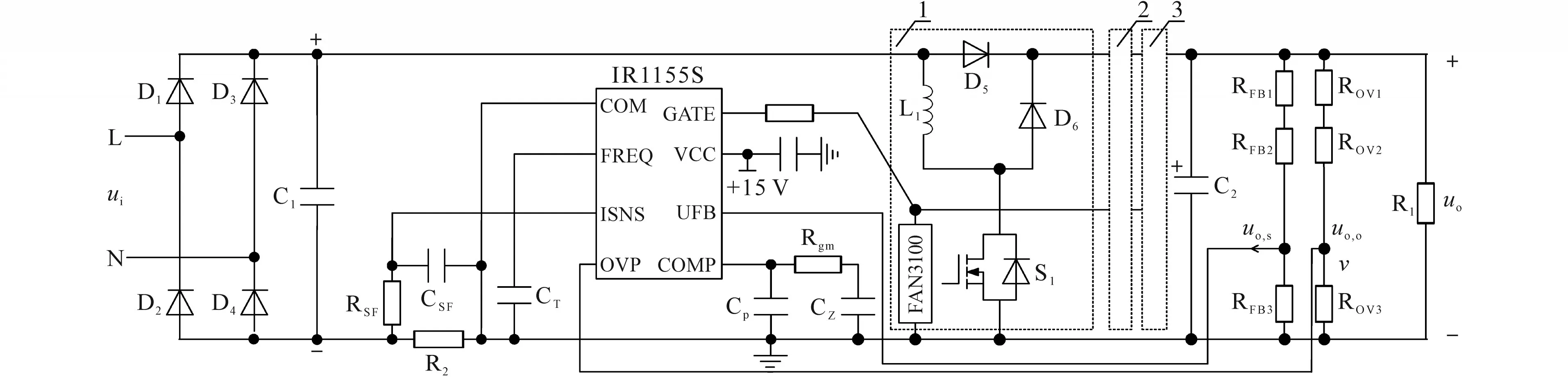
图6 基于IR1155S的开关电感级联型高倍升压AC-DC变换器Fig.6 Switched inductor cascaded high transfer-ratio Boost AC-DC converter based on IR1155S

2.1 各部分传递函数

基于IR1155S 高倍升压单相AC-DC 变换器的小信号模型电路如图7所示。

图7 IR1155S APFC小信号模型Fig.7 Small signal model of IR1155S APFC

图7 中，H1（s）为输出分压器传递函数；H2（s）为电压误差放大器和补偿器传递函数；H3（s）为单周期控制调制器传递函数；G（s）为功率电路的传递函数。整个环路的开环传递函数[12-13]T(s)如下式所示：

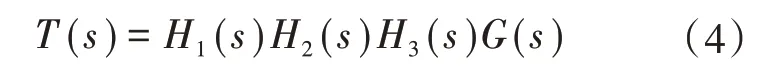
纯阻性负载时，功率电路传递函数G(s)为

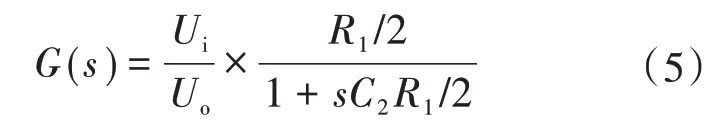
式中：Ui为输入电压有效值；Uo为输出电压平均值；R1为负载电阻；C2为输出电容。

输出分压器传递函数H1(s)为

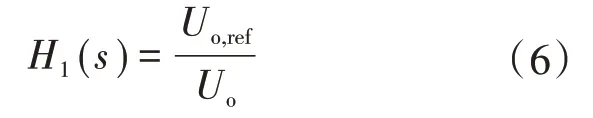
式中：Uo,ref为IR1155S内部参考电压。

IR1155S 芯片COMP 引脚外接软启动电容CZ、跨导电阻Rgm、极点电容CP构成跨导型电压误差放大器，作为输出电压补偿网络。输出电压补偿器传递函数H2(s)为

式中：gm为跨导，取值50µS。

单周期控制调制器传递函数H3（s）为

式中：R2为采样电阻；GDC为直流增益，GDC=3.1。

2.2 输出电压补偿网络设计步骤

2.2.1 选择软启动电容CZ

基于软启动时间选择CZ，软启动时间选取典型值40 ms。软启动时间内COMP 引脚电压UCOMP从0升至最大值。软启动电容为

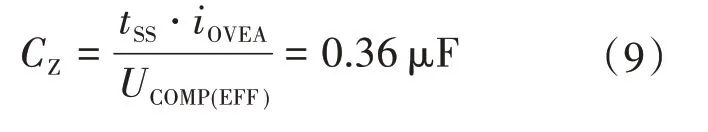
式中：iOVEA为源电流，iOVEA=44µA；UCOMP（EFF）为有效COMP 管脚电压，UCOMP（EFF）=4.9 V；tss为软启动时间，tss=40 ms。

可选择CZ=0.33µF。

2.2.2 选择跨导电阻Rgm

Rgm的选择应该确保H1（s）H2（s）的2倍网频衰减量足够小，以此避免网侧电流畸变。设效率为92%，首先计算出2 倍网频纹波电压幅值，考虑最低网频fAC=47 Hz，此时出现最大纹波电压，则峰-零纹波电压UOPK为

输出电压中峰-峰纹波电压为2UOPK，经过电阻分压和误差放大器补偿网络，该电压反映到UCOMP，引起ΔUCOMP。与误差放大器输出电压摆幅UCOMP（EFF）相比，ΔUCOMP应足够小，选择ΔUCOMP/UCOMP变化范围为1.0%，以获得较高相位裕量和在负载阶跃时较低振荡响应。1.0%衰减要求为

式中：GVA为H（1s）H（2s）在2倍网频下所需的衰减量。而且，H1(s)=Uo,ref/Uo，即

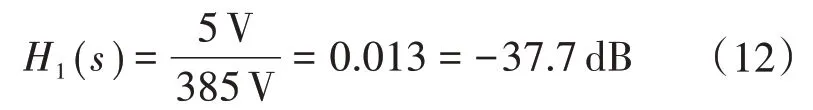
因此2倍网频处仅仅来自H2（s）的所需衰减为

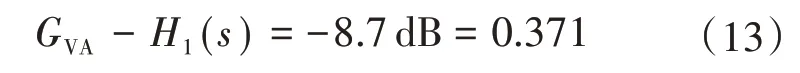
由于电压补偿器极点的设置应该远高于2倍网频，因此CZ≫CP，则在2 倍网频处误差放大器传递函数可以近似为

由于CZ已经确定，只需计算Rgm，计算公式为

阻性负载时，功率电路传递函数中零点对应频率可以估算为

功率电路传递函数中的极点频率为

2.2.3 选择极点电容CP

根据高频极点位置选择CP。极点频率的选择应较高于交越频率、远低于开关频率，本文中选择1/6×fsw，可得：

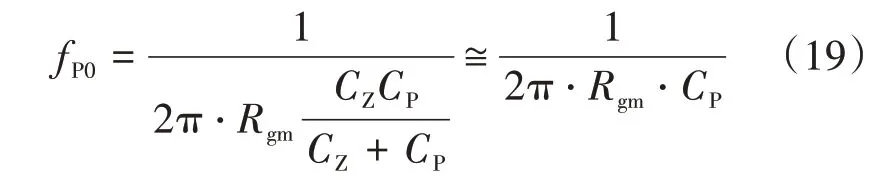
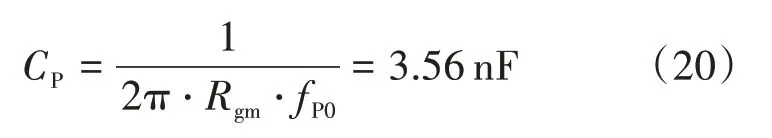
2.2.4 估算相位裕量

满载1.0 kW 时，交流输入电压为85 V的电压环幅频和相频响应如图8 所示。此时，交越频率为5 Hz，相位裕量约为28.2°，该结果满足交越频率和相位裕量的设计要求。

图8 AC 85 V/1.0 kW时OCC APFC开环的频率特性Fig.8 Frequency characteristics of the open-loop of OCC APFC at AC 85 V/1.0 kW

3 仿真与实验验证

为验证理论分析正确性，对本文所提的AC-DC变换器仿真验证并搭建实验样机。仿真及实验参数如下：输入电压85 V/50 Hz，开关频率50 kHz，输出电压平均值385 V，输出功率1 kW，电感L1=L2=L3=500µH。

3.1 实验波形

仿真时，分压比100∶1，为消除纹波电压影响和获得385 V 均值，给定电压为4 V，采用双闭环控制，内环控制策略为PI 调节器。图9 为在感量相等时CCM 下的仿真电路，图10 为此条件下电感电流波形，图11 为输入电压、输入电流和输出电压波形。

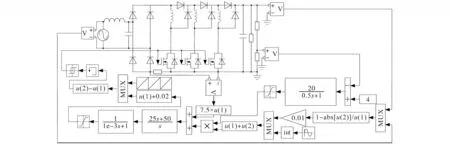
图9 感量相等时CCM下的仿真电路Fig.9 Simulation circuit in CCM with equal inductance

图10 仿真中感量相等时CCM下电感电流波形Fig.10 Simulated waveforms of inductor currents in CCM with equal inductances

图11 仿真中感量相等时CCM下输入电压、电流、输出电压波形Fig.11 Simulated waveforms of input voltage，current and output voltage in CCM with equal inductances

该实验样机采用IR1155S芯片作为核心模拟控制芯片，实验平台如图12 所示。关键参数（参数名与图6 对应）如下：最大输入电流12.81 A，最大负载1 kW，输出电容C2=2×470µF/450 V；交流滤波电容C1=0.47 µF，分流电阻R2=30 mΩ，滤波电阻RSF=100 Ω，滤波电容CSF=1.0 nF；电压反馈支路RFB1=RFB2=499 kΩ，RFB3=13 kΩ；过压保护支路ROVP1=ROVP2=499 kΩ，ROVP3=12.8 kΩ；谐振电容CT=1 850 pF，软启动电容CZ=0.33 µF，跨导电阻Rgm=5.36 kΩ，极点电容CP=3.56 nF。

图12 开关电感级联AC-DC变换器实验平台Fig.12 Experimental platform of switched inductor cascaded AC-DC converter

输入电压为85 V/50 Hz，输出电压为385 V，负载为600 W时，测得网侧功率因数为1。该ACDC变换器的关键波形如图13～图15所示。其中，图13为该AC-DC变换器输入电压曲线、输出电压纹波曲线和输入电流曲线，图14为该AC-DC 变换器的三个开关脉冲曲线1～3 与输入电流曲线波形，图15为该AC-DC变换器的电感电流波形。

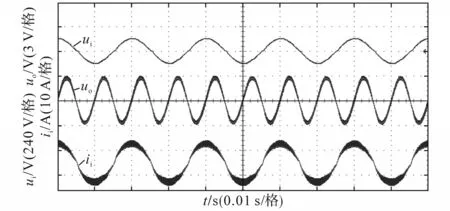
图13 输入电压、输出电压纹波、输入电流Fig.13 Waveforms of input voltage，output voltage ripple and input current

图14 开关脉冲及输入电流波形Fig.14 Waveforms of switching pulse and input current

3.2 实验结果分析

从图10、图11、图13 和图15 可以看出，该AC-DC 变换器双闭环控制与单周期控制皆可采用，控制简单，且交流侧功率因数高，实验测得网侧功率因数为1，说明该AC-DC 变换器具有良好的功率因数校正能力。再者电感值在实际运行时总会受到流经电流大小以及磁芯饱和程度的影响，故而感量完全相同不会实现，但在实验中，该变换器运行安全稳定，说明该变换器能在感量不等时运行，验证了感量不等CCM 下理论分析的正确性，也表明该AC-DC变换器具有运行安全稳定性。从图14 可以看出，采用IR1155S 单周期控制，三个开关脉冲同步性良好，证明多级级联时该变换器可使用同一驱动器，节省成本。

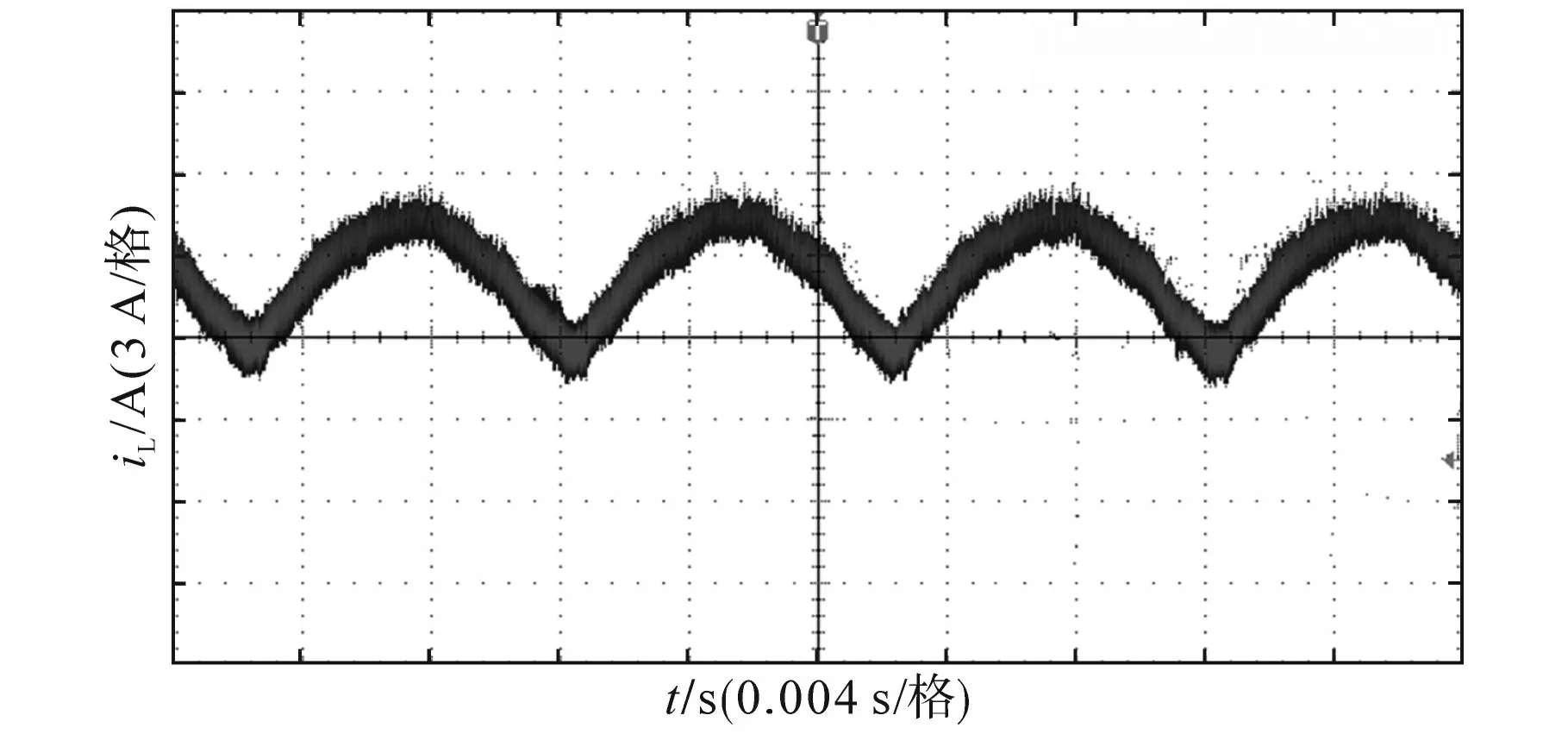
图15 电感电流波形Fig.15 Waveform of inductor current

4 结论

采用并联充电、串联放电原理，提出了一种开关电感级联型高倍升压能力的AC-DC 变换器拓扑，给出了感量相等和不等时CCM 下的关键波形，基于模拟控制器IR1155S设计了感量相等时、单周期控制、CCM 下的实现方案，并对该AC-DC变换器进行仿真与实验验证。研究结论如下：该AC-DC 变换器具有高倍升压能力、功率因数校正能力以及运行安全稳定等优点，解决了现有开关电感型AC-DC 变换器无法级联拓展以获得更高升压比以及感量不等时造成的超高浪涌电压问题。同时，感量不等时大电感出现的恒定电流平台值得进一步思考其应用场合。