海岛局部风场特性的风洞试验和数值模拟研究

郭健 ，胡成杰

(1.西南交通大学 土木工程学院，四川 成都 610031；2.浙江工业大学 桥梁工程研究所，浙江 杭州 310023)

1 引言

跨海工程往往需要在坡度较大的海中小岛上选址以设置主塔基础，从而尽可能减小跨海桥梁的跨径，降低技术风险和造价，如主跨1 650 m 的舟山西堠门大桥[1]，北塔位于海岛老虎山上，其陡峭处坡度近31°；另一座跨海悬索桥双屿门大桥的一个初步设计方案拟定了主跨1 770 m，西塔位于海岛鲎山上，坡度10°左右。沿海地区的高压输电线路为避免长距离输送而往往在海岛上设塔，如宁波–舟山六横岛附近的高耸输电铁塔建设便采用在海岛上设塔的设计方案。然而在复杂的海洋强风环境下，气流在经过海岛地形时会受到地形挤压而引起明显的局部风效应，由此会产生平均风加速区，使得平均风剖面与平地相应位置的平均风剖面存在差异，因此在海岛上的跨海桥塔和输电塔架等工程结构的抗风设计及施工临时结构都需要准确把握局部风效应带来的平均风速差异，这对于保证工程安全十分重要。过去对于特殊微地形风场的研究主要是针对丘陵等山地地形，近年来，随着海洋开发和近海工程建设的增加，扩展到对海岛的研究。肖仪清等[2]利用计算流体动力学（Computational Fluid Dynamics，CFD）方法对复杂地形进行风场分析。Wang 等[3]和Cao 等[4]通过CFD 二维数值模拟来研究山体表面粗糙度、坡度与来流湍流对山地风场的影响；李正良等[5]和孙毅等[6]借助风洞试验与Fluent 软件对三维山地模型进行研究，讨论了坡度、高度与地貌因素对山地平均风加速效应的影响；李正昊等[7]通过CFD 数值风洞来研究山脉长度、坡度以及山脉间距对垭口内平均风速的影响并对峡谷地形的平均风加速效应进行了研究；陈政清等[8]对山区峡谷进行风洞试验，表明峡谷地貌的存在使得不同位置处的风剖面存在较明显差异。再者，文献[9–10]应用CFD 方法对桥址区地形风场空间分布进行研究，为桥梁抗风设计提供了参考。此外，Vladut 等[11]结合边界层风洞试验和数值模拟来研究一座真实海岛的绕流现象；杨秋彦等[12]针对一次海风过程，对海南岛上地形的局部海风环流影响进行了数值模拟，以探讨地形对海风环流的影响。

上述研究为海岛地形风场分析提供了有利条件，然而考虑到海岛风场变化的复杂性，以具体海岛为对象所开展的研究还不具有普遍性；风剖面指数分布还有待了解；对平均风加速区以及加速比和差异系数受海岛坡度与高度的影响还有待进一步研究，对迎风侧和背风侧典型位置的顺风向、横风向和竖向湍流强度和阵风因子分布还需深入探讨。总的来看，有必要通过典型特征模拟并以理想形态海岛为对象来开展局部平均风效应和脉动风效应研究，这对于海岛工程建设，例如跨海工程塔架选址和抗风设计等意义重大。

2 工程概况

随着海岛工程建设进度加快，近20 年来，在季风盛行、风况复杂的我国东部海域建设了多座跨海大桥和高耸钢管塔输电线路，风场特性的变化是海岛工程结构物选址、设计和施工考虑的重点。浙江沿海岛礁众多，其海岛形状特征与海拔高度各有差别，如宁波舟山海域的典型岛礁海拔可达200 m。和陆地相比，海洋大气下垫面性质更均一，表面粗糙度低，湍流强度小[13]。舟山群岛地区的风速和风力较内陆地区明显偏大[14–16]。如图1 所示为宁波–舟山港的六横岛海域，该海域有多个跨海工程建设规划，多个海中小岛被选择来建设桥梁塔结构和高耸输电铁塔，从而能够避免桥梁跨过海以及高压输电线路长距离跨越所带来的一系列技术困难。针对该海域岛礁石的局部风效应突出的问题，开展了风洞试验和数值模拟研究。

图1 宁波–舟山港的六横岛海域Fig.1 Sea area of Liuheng Island in Ningbo-Zhoushan Port

3 风洞试验概况

本文参照多个典型实地海岛，进行了缩尺简化以拟定所研究的海岛模型尺寸，根据拟定的缩尺模型尺寸制作了多个不同坡度的海岛模型，并主要参考宁波舟山海域的环境风场以及结合风洞试验来研究海岛局部风场特征，以期为实际海岛工程建设提供抗风参考依据。

3.1 海岛缩尺模型概况及测点布置

为分析海岛坡度和高度对局部风效应的影响，考虑宁波舟山地区实际海岛地形的典型形态，对实际海岛进行了理想化处理，采用具有代表性的余弦型曲面进行研究[17]，曲面形式定义如式（1）所示。海岛截面轮廓如图2a 所示。

式中，H为海岛高度；D为海岛底面直径；z为所对应的高度；(x,y)为圆形底面内坐标。

通过1∶500 的几何缩尺比来制作相应的海岛模型，模型骨架材质为挤塑板，表面覆盖草绒，模型高度为0.2 m，坡度（2H/D）取15°、25°、35° 3 个工况（表1）。按对称性在坡面上布置了11 个定位点（A1−A11），在每个定位点的垂直上方各布置了10 个测点，具体布置见图2。

图2 风洞试验示意Fig.2 Schematic diagram of wind tunnel test

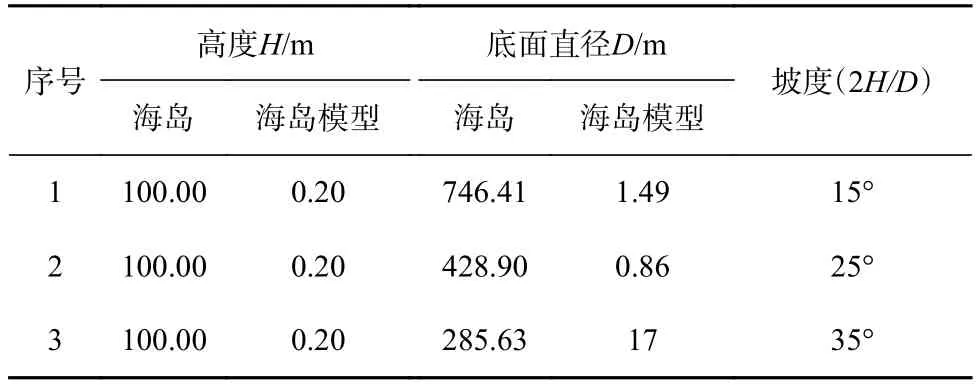
表1 海岛参数Table 1 Island parameters

3.2 边界层A 类风场模拟

本次边界层风洞试验段的截面尺寸为5 m（高）×8 m（宽），最高风速可达40 m/s，风速测量采用澳大利亚TFI（Turbulent Flow Instrumentation）公司的眼镜蛇风速探头。采用尖劈和粗糙元来模拟相关规范A 类粗糙度[15–16]大气边界层风场，边界层风场风剖面指数α=0.12，来流为1∶500 的A 类地貌来流；未缩尺风场10 m 高度处基准风速为43.29 m/s（综合参考相关规范[15–16]，取舟山地区基本风压0.85 kN/m2，并考虑A 类与B 类地貌基本风速转换系数1.174 来换算），梯度风高度为300 m，离地700 m 高度的理论风速为72 m/s。缩尺后风场的梯度风高度为0.6 m，离地1.4 m 高度处的风速Vr=13.41 m/s，风速缩尺比为13.41/72=1∶5.37。本次风洞试验的布置如图3 所示，平均风剖面及湍流度剖面如图4 所示。

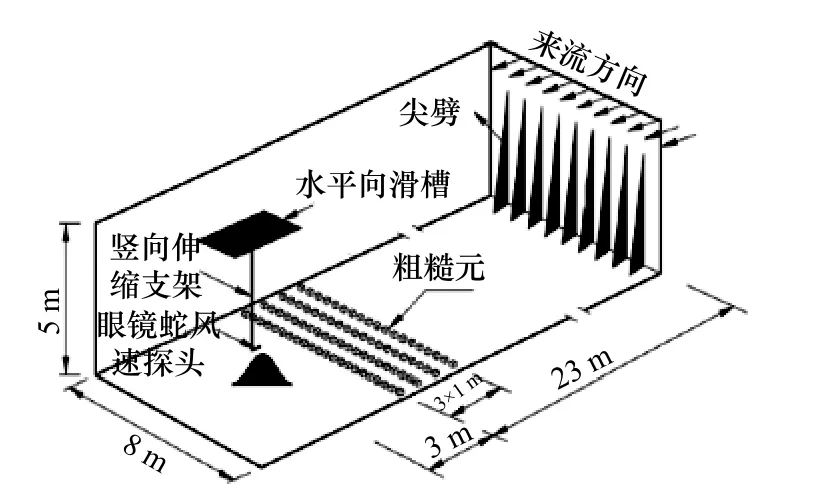
图3 风洞试验布置Fig.3 Layout of wind tunnel test

图4 边界层平均风剖面及湍流度剖面Fig.4 Mean wind and turbulence profiles of boundary layer

4 CFD 数值模拟

为了更好地进行对比研究，利用CFD 模拟高度为100 m、坡度为15°、25°和35°的海岛局部风场。

4.1 模型建立与网格划分

计算域高度为600 m（6H），入口距迎风坡最小距离为3D，出口距海岛背风坡最小距离为5D，宽度取5D，所有工况模型阻塞率为1.67%，满足不大于5%的要求，以保证计算域内流体充分发展，提高计算精度（具体计算域见图5a）。

采用结构化六面体网格对计算域进行离散处理；对海岛表面网格进行适当加密处理，最大网格尺寸为8 m，并以1.1 的增长率向外扩散，水平最大网格尺寸为50 m；为保证计算精度考虑了地表粗糙度等因素[2]，竖向第一层网格高度为1 m[18]，竖向增长率为1.1（网格划分见图5b，图5c）。

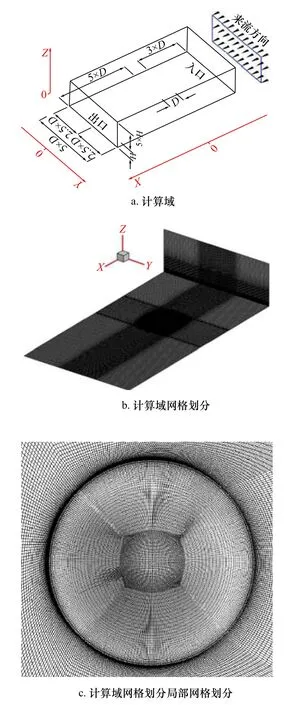
图5 计算域及网格划分示意图Fig.5 Schematic diagram of computing domain and grid

4.2 模拟参数设置

采用Realizablek-ε模型[19]，壁面函数采用考虑压力梯度的非平衡壁面函数，符合实际气流在模型表面会产生分离、附着、冲击等复杂流动现象；入口采用速度入口，入口处平均风速剖面、湍流动能和湍流耗散率剖面自定义；出口为自由流出出口，让其尾流充分发展；两侧面和顶面均采用对称边界，保证垂直于对称边界的速度等物理量的梯度为0；底面和海岛表面均采用无滑移壁面，表面切向风速为0；考虑实际地面粗糙度的影响，设置底面和海岛表面的砂砾粗糙度高度分别为0.5 m 和1 m。采用定常计算，压力–速度求解采用SIMPLEC 算法，同时用二阶迎风格式对控制方程进行离散处理，并适当调整松弛系数的大小，以保证计算速度和精度。

边界的自保持性[20]，指的是风剖面在未到达目标物之前能在流场中保持不变。入口的平均风速剖面V(z)、湍流动能k(z)和湍流耗散率ε自定义边界条件如式（2）至式（6）所示，将公式以C 语言程序形式通过Fluent 中的UDF 功能接入，以满足相应流场速度和湍流特性的要求。

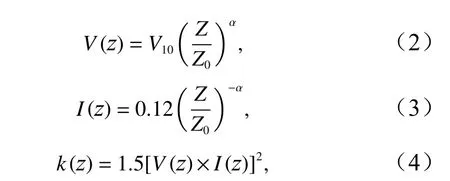
式中，Z0和V10分别表示A 类地貌条件标准高度（10 m）和标准高度处的平均风速（43.29 m/s）；I(z)为z高度下的湍流度；Lu为湍流积分尺度，参考文献[21]；Cμ取0.09。该边界条件可以使入口处的风剖面较好的作用在海岛，风剖面自保持性良好。图6 为风剖面自保持性的验证，U为来流风速。图7 为模型水平向风速示意，在入口和出口处体现了水平向风速沿高度方向的变化。

图6 风剖面自保持性验证Fig.6 Verification of wind profile self preservation

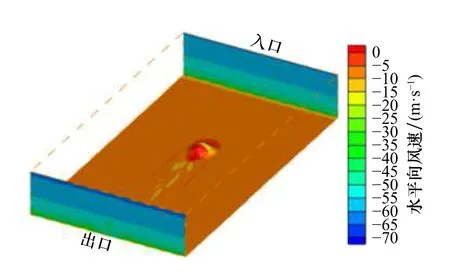
图7 水平向风速示意图Fig.7 Schematic diagram of horizontal wind speed

5 CFD 研究局部平均风效应

5.1 CFD 数值模拟与风洞试验对比分析

如图8 所示风洞试验数据为风洞实测数据经风速缩尺比转换而来。将CFD 数值模拟所得的各测点平均风速与风洞试验数据进行对比，如图9 所示，绝大部分数据误差小于20%，且多数误差小于10%。迎风侧数据误差较小，背风侧误差略大，其误差略大处主要集中在背风侧的海岛表面附近测点。一方面由于风洞试验过程中靠近模型表面与背风侧风速受模型遮挡难以测定，另一方面可能由于数值模拟过程中表面粗糙度的影响，总体而言，数值模拟结果具有一定的可靠度。

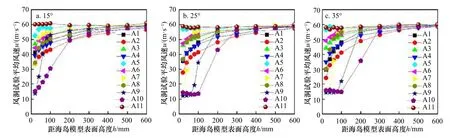
图8 不同坡度海岛风洞试验平均风速分布Fig.8 Average wind speed distribution of wind tunnel test on islands with different slopes

图9 不同坡度海岛风洞试验与数值模拟平均风速对比Fig.9 Comparison of mean wind speed between wind tunnel test and numerical simulation on islands with different slopes

由于风洞试验的工况有限，在满足初步精度的要求下，利用前述CFD 数值模拟手段，对多工况海岛的风剖面指数、最大加速比和差异系数的分布进行拓展研究。

5.2 典型位置的风剖面指数分布

基于CFD 数值模拟和风洞试验结果，对典型位置的风剖面指数进行拟合，在拟合算法中作为全局优化搜索方法的遗传算法由于并非进行指定的路径进行探索，而是基于概率控制探索，仅仅通过其特有的选择、交叉和变异运算就可以快速探索到最优解，因此十分适用于非线性模型曲线的拟合[22]。

这里对3 种坡度工况的风洞试验和数值模拟风剖面采用了遗传算法进行指数率分布拟合[23–26]，具体拟合曲线如式（7）所示，得到典型位置处的风剖面指数分布如图10 所示。

从图10 可以看出，3 种坡度工况的风剖面指数分布相似；A10 处风剖面指数较大，迎风侧风剖面指数大于背风侧。

图10 典型位置风剖面指数（α）Fig.10 Wind profile index at typical location (α)

5.3 迎风岛脊线的风剖面差异性分析

这里引入无量纲参数——加速比 ∆Sz[5,8]以及自定义参数— —风剖面差异系数W来分析局部风效应，以此来揭示海岛平均风剖面相比于平地相应位置平均风剖面的差异性，结果值越大带来的风场改变越大，风剖面的差异性越明显，风效应越突出。风剖面差异系数W和加速比 ∆Sz的具体表达见式（8）和式（9）。

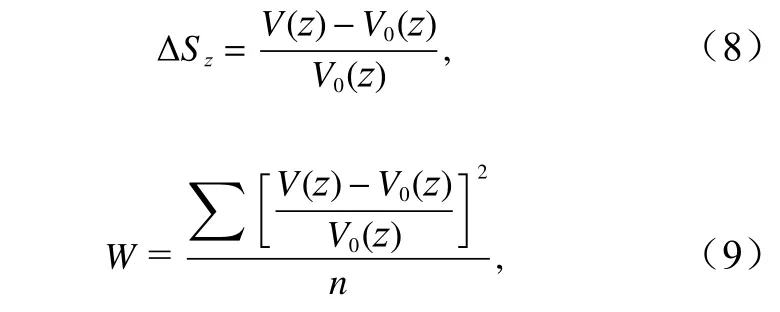
式中，∆Sz为z高度处的加速比；V(z)表示海岛表面以上z高度处的平均风速，V0(z)表示平地地表以上z高度处的平均风速；n表示高度方向测点数，n取10。

沿坡度35°海岛的迎风坡每隔15°取一条岛脊线，每条岛脊线上布置11 个定位点，具体布置见图11，并在每个定位点的垂直上方各布置了10 个测点，布置参考图2c。

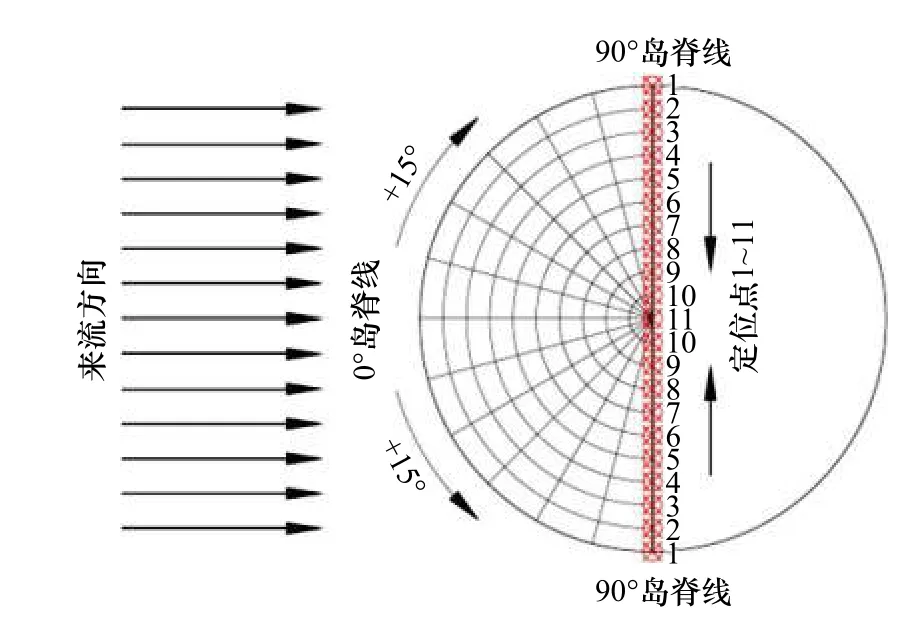
图11 岛脊线与定位点布置Fig.11 Island ridge lines and points layout

如图12a 所示，最大加速比随岛脊线角度的增加而增加；45°～60°的最大加速比变化梯度最大；最大加速比出现在坡顶区域。最大加速比大于0 表明平均风爬坡引起加速效应，小于0 的区域反映了海岛对于气流的阻挡。随着岛脊线角度的增加，所在岛脊线的加速区会下移。

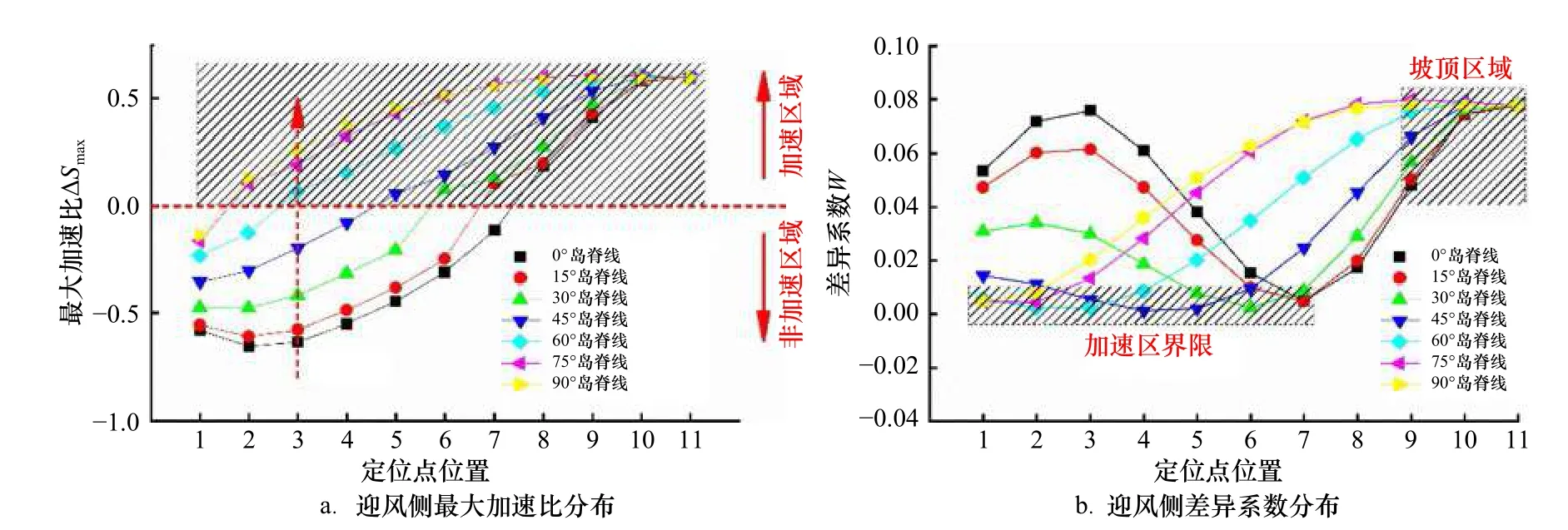
图12 迎风侧最大加速比与差异系数分布Fig.12 Maximum acceleration ratio and difference factor distribution on windward side

如图12b 所示，差异系数沿岛脊线分布以45°岛脊线为界呈现两种变化趋势；差异系数为0 的位置随岛脊线角度的增加有沿岛脊线向坡脚靠近的趋势；坡脚处的差异系数随着岛脊线角度的增加而减小；差异系数最大值出现在坡顶区域。差异系数为0 的位置是平均风剖面与平地相应位置平均风剖面差异性最小处，沿岛脊线向坡顶方向是加速区，向坡底方向是阻挡减速区。坡腰位置的差异系数较低，与平地相应位置的风剖面差异性较小。

5.4 坡度和高度对加速比及差异系数的影响

为研究海岛坡度对于局部风场的影响，采用上述CFD 模拟手段，对局部风效应较明显的0°岛脊线进行研究，计算了高度为100 m，坡度为10°～45°共8 种模型。如图13a 所示为最大加速比和差异系数随海岛坡度的变化规律。坡顶处（0°岛脊线顶部）的最大加速比在0.4～0.8 之间，最大值出现在25°附近；在1/2 坡腰（0°岛脊线中部）、坡底（0°岛脊线底部）处，随着坡度的增加最大加速比有减小趋势。25°坡顶处的差异系数最大，与平地相应位置的风剖面差异性最大；1/2 坡腰处的差异系数随着坡度的增加而增加；坡底处差异系数随着坡度的增加先增加后趋于稳定。1/2 坡腰处的差异系数较小，与平地相应位置的风剖面差异性较小。

图13 不同坡度和高度的加速比及差异系数分布Fig.13 Distribution of acceleration ratio and difference factor for different slopes and heights

为研究海岛高度对于局部风场的影响，借助CFD模拟了坡度为35°，高度50～300 m 共5 种工况，对局部风效应较明显的0°岛脊线进行研究。如图13b所示为最大加速比和差异系数随海岛高度的变化规律。坡顶（0°岛脊线顶部）最大加速比在0.5～1.0 之间，坡顶处的最大加速比和差异系数变化趋势一致，随着高度的增加其值有增加的趋势，在50～150 m 变化不大，150～300 m 变化较明显；1/2 坡腰处（0°岛脊线中部）最大加速比和差异系数变化趋势相反，最大加速比随着高度的增加而减小，差异系数则随着高度的增加而增加。1/2 坡腰处的风剖面差异性随着高度的增加而变大。

6 局部脉动风效应

3 种坡度工况下的脉动风效应也存在着一定的差异，而脉动风效应差异的具体分析对于海岛工程建设中抗风稳定性的考虑有着指导作用。

由于风的不规则性引起的脉动风一般周期短，与一些工程结构的自振周期较为接近，会使结构产生动力响应。特别是对于高耸构筑物等柔性工程结构，脉动风带来的风振动力响应明显，会对工程结构的施工和运营等造成明显影响。因此对海岛附近描述脉动风强度的两个重要特征量——湍流强度和阵风因子的具体分析显得至关重要。

湍流强度通常定义为基本时距内某一高度脉动风速标准差与平均风速的比值。阵风因子定义为阵风持续时间内最大阵风风速与基本时距内平均风速的比值。基于风洞试验结果，得到了图2c 中各定位点（即距实际海岛表面10 m、20 m、30 m、40 m、50 m、100 m、150 m、200 m、250 m、300 m）处顺风向、横风向和竖向的湍流强度和阵风因子分布情况，如图14至图16 所示。

由图14 可以看出，3 种坡度工况下坡顶处顺风向、横风向和竖向湍流强度沿高度的变化和空风洞下测得的湍流强度沿高度的变化较接近；

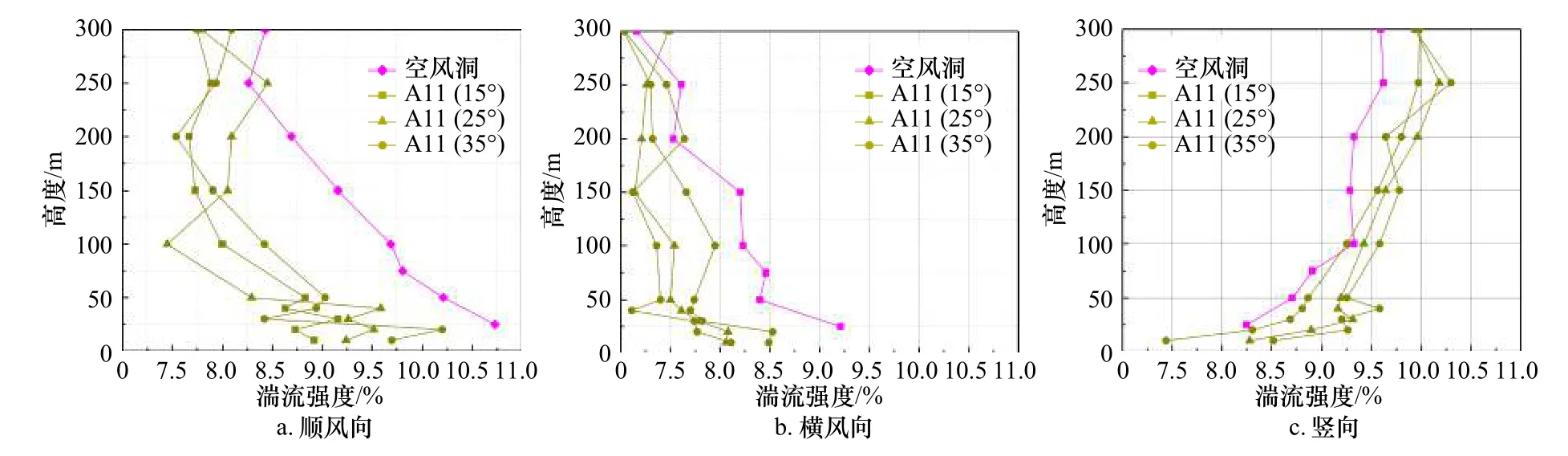
图14 坡顶（A11）湍流强度和空风洞的湍流强度对比Fig.14 Comparison of turbulence intensity between top of slope (A11) and air tunnel

在顺风向和横风向，距定位点200 m 高度内（即2 倍海岛高度）湍流强度变化较大，反映了海岛地形对于坡顶湍流强度的影响，而坡顶竖向的湍流强度受海岛地形的影响较小。

由图15 可知，迎风侧的三向湍流强度分布较规律，而背风侧的三向湍流强度分布较为混乱，尤其是在距海岛表面100 m 高度内，反映了风绕流后的扰动较大；不同坡度迎风侧的湍流强度较为接近，而背风侧的湍流强度有较大差异，在距海岛表面50 m 内，坡度越大背风侧的湍流强度越小；对于迎风侧，湍流强度沿着高度方向仍具有指数率分布的趋势，对于背风侧，湍流强度分布仍需开展更为细致的研究。

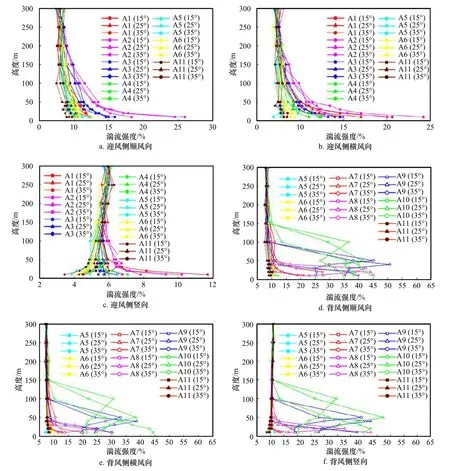
图15 迎风侧和背风侧湍流强度分布Fig.15 Turbulence intensity distribution on windward and leeward sides

由图15 和图16 可以看出，不同坡度和不同高度的湍流强度和阵风因子变化趋势较为接近，具有较高的一致性。

图16 迎风侧和背风侧阵风因子分布Fig.16 Gust factor distribution on windward and leeward sides

7 结论

本文通过风洞试验和数值模拟对典型余弦型海岛的局部风场进行研究，得到如下结论：

（1）坡顶沿高度方向的平均风速变化不大，该处风剖面指数非常小，迎风侧风剖面指数较小，背风侧风剖面指数较大；加速效果靠近坡顶位置尤为突出；坡腰某一位置为加速区与非加速区分界线，坡顶处最大加速比在0.4～1 之间，差异系数较大；坡顶处与平地相应位置平均风剖面差异性较大，坡腰处风剖面差异性较小。

（2）高度一定时，随着坡度的增加，0°岛脊线差异系数为0 处有下降趋势；坡度一定时，随着高度的增加，0°岛脊线差异系数为0 处会愈加远离1/2 坡腰位置下移；坡顶最大加速比随坡度的增加而增加，在坡度为10°～30°时增加较明显；坡顶最大加速比随高度的增加而增加，在高度为150～300 m 时增加较明显。海岛迎风坡度为25°左右时，0°岛脊线上最大加速比和差异系数均较大，风剖面差异性较大，局部平均风效应突出，应当在工程中特别关注。

（3）湍流强度和阵风因子的变化趋势具有较高的一致性。在迎风侧，湍流强度沿着高度仍具有指数率分布的趋势，而在背风侧，湍流强度分布仍需开展更为细致的研究。在顺风向和横风向，距定位点200 m高度内（即2 倍海岛高度）湍流强度变化较大，而竖向的湍流强度受海岛地形的影响较小；迎风侧的三向湍流强度分布较规律，而背风侧的三向湍流强度分布较为混乱，尤其是在距海岛表面100 m 高度内，这在背风侧海岛工程建设中要特别予以关注。