南黄海透明度的时空分异特征及影响因素分析
叶晗,史玥双,梁涵玮,毛颖,周振宇,郑秀蕊,王胜强*,孙德勇
(1.南京信息工程大学 海洋科学学院,江苏 南京 210044;2.自然资源部海岸带开发与保护重点实验室,江苏 南京 210024;3.南京信息工程大学 地理科学学院,江苏 南京 210044;4.福建省气象灾害防御技术中心,福建 福州 350005;5.南京信息工程大学 长望学院,江苏 南京 210044)
1 引言
水体透明度(Zsd)指光穿透水体的程度,能够有效反映水体的浑浊程度,是评价水体水质最为直观的光学参数[1–2]之一。水体透明度的变化与诸多海洋生物化学过程和水动力环境过程密切相关,如海洋初级生产力、物质输送等[1],因此研究水体透明度的变化特征对于海洋水团分析、初级生产力研究、海洋生态环境保护等具有重要的意义[3]。
对于Zsd的监测,传统方法常采用赛克盘进行现场测量[4–5],该方法耗时耗力,而且调查样本有限,难以获取Zsd有效的时空分布信息。相比之下,卫星遥感技术具有覆盖范围广、动态性强等诸多优势,逐渐成为Zsd的主要监测方法。目前针对Zsd的卫星遥感反演算法大致可以分成两类:经验算法和分析/半分析算法[6]。经验算法主要通过建立Zsd和遥感反射率光谱之间的经验定量关系,从而实现对Zsd的反演,该方法往往依赖于大量的现场数据,区域性较强;分析/半分析方法则基于Zsd与水体光学特性之间的物理理论关系,来实现对Zsd的遥感反演,模型机理清晰、普适性好[7–8]。
近年来,Lee 等[9]通过光学理论推导修正了传统的Zsd理论模型,提出了新的Zsd理论模型,该理论模型的核心输入参数是水体漫衰减系数(Kd)。基于此,Lee 等[9]利用半分析算法(Quasi-analytical Algorithm,QAA)从遥感影像先反演了Kd,进而估算了全球海洋的Zsd。当研究者们将Lee 等[9]的模型用于区域水体时,发现新的Zsd理论模型在整体上表现出良好的普适性[10–12],然而QAA 算法反演的Kd在某些区域(如近岸浑浊水体)存在一定的偏差,这导致Zsd的遥感反演精度不高,因此,在实际应用中需要根据研究水域的水体光学特性对Kd进行重新遥感反演。例如,Mao 等[10]和毛颖等[13]针对渤海、黄海海域提出了Kd的加权联合反演算法,再利用Lee 等[9]的新理论模型从地球静止水色仪(Geostationary Ocean Color Imager,GOCI)传感器数据反演了Zsd,结果与现场实测数据相比具有很好的一致性。
南黄海海域中国沿岸受到陆地径流输入、季风、洋流等因素影响,水体特性复杂多变[14],另外沿岸地区人类活动强度高,对近岸海洋环境的影响越来越引起人们的关注[15–16]。因此,本文以南黄海为研究区域,通过优化校正Mao 等[10]的Zsd算法,使其适用于中等分辨率成像光谱仪(Moderate Resolution Imaging Spectroradiometer,MODIS)传感器,进而利用MODIS 长时序的遥感数据资料,分析揭示近20 年(2002–2020 年)南黄海水体透明度的时空变化特征,并探讨其影响因素。
2 研究区域与数据方法
2.1 研究区域
本文以南黄海海域为研究区域,具体的经纬度范围为30.8°~36.7°N,119°~126.9°E(图1)。此外,为深入分析Zsd的时间变化特征及其影响因素,本文选取了4 个具有代表性的子区域(如图1 红色方框所示),包括:(1)南黄海中部(Central South Yellow Sea,CSYS),经纬度为34.7°~35.7°N,123.8°~124.8°E,面积为9 101.2 km2。(2)南黄海南部(Southern South Yellow Sea,SSYS),经纬度为32.7°~33.7°N,124.2°~125.2°E,面积为9 101.2 km2;CSYS 和SSYS 代表了水体较为清澈的外海海域,选取这两个区域可以对比分析近岸与外海Zsd的时空分布及其驱动因素的差异性。(3)长江口(Changjiang River Estuary,CRE),经纬度为31°~31.7°N,122°~122.8°E,面积为5 096.7 km2;该海域代表了长江冲淡水影响区域,选取该海域的目的是对比凸显南黄海海域Zsd的季节性变化以及悬浮物对其的影响特征。(4)江苏近海(Jiangsu Coast,JC),从左到右,从上到下4 个顶点的经纬度分别为(34.8°N,119.2°E),(34.6°N,120.6°E),(32.8°N,122°E),(32°N,121.8°E),总面积为21 615.3 km2;该海域为典型的近岸海域,其受潮汐影响明显,水体常年处于浑浊状态,此外,江苏近岸人类活动频繁,对Zsd也可能存在一定的影响,因而选作代表性区域之一。
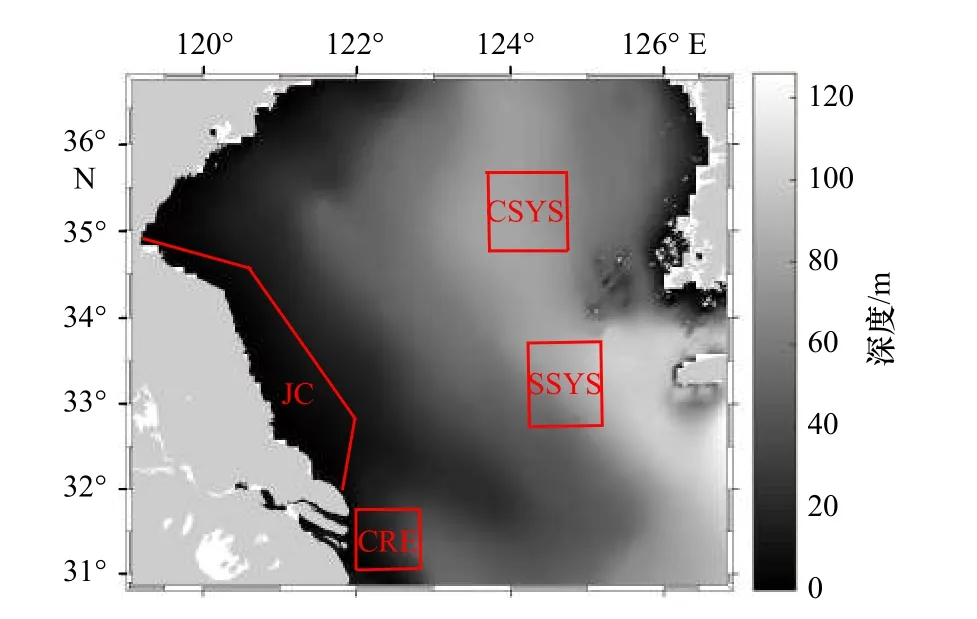
图1 研究区域图Fig.1 The study area
2.2 透明度遥感模型
Lee 等[9]提出的新的Zsd理论模型可表示为
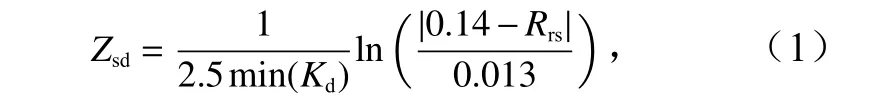
式中,Kd表示下行辐照度的漫衰减系数(单位:m−1);Rrs表示与Kd相同波段的遥感反射率;min 表示所有波段对应的Kd最小值。对于Kd的计算,Lee 等[9]建立了如下反演模型
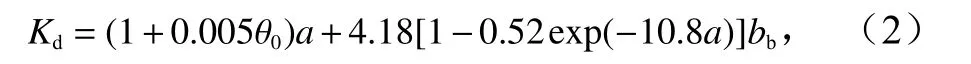
式中,θ0表示太阳天顶角;a表示水体总吸收系数(单位:m−1);bb表示水体总后向散射系数(单位:m−1),对于a和bb的计算,Lee 等[9]采用了QAA 模型[17]。然而,Mao 等[10]和毛颖等[13]发现QAA 模型反演的Kd在黄海、渤海近岸浑浊水体存在一定误差,使得透明度反演精度较低。为此,Mao 等[10]和毛颖等[13]提出了Kd遥感反演联合算法,以提高Kd的遥感反演精度,具体表示为

式中,Kd_hybrid表示联合算法计算的Kd;Kd_clear为清澈水体的漫衰减系数,仍由QAA 模型计算;Kd_turbid为浑浊水体的漫衰减系数,由针对黄海、渤海近岸浑浊水体的区域算法计算[13]。Kd_turbid的计算最后仍然使用的是式(2),但是其a(490)和bb(490)的计算方法有所不同,如式(4)、式(5)和式(6)所示:

式中,f=0.305;Q=4;B=1.13;bbw(490)=1.1×10−3;aw(665)=0.309;bbw(665)=3×10−4。式(3)中的w1和w2为权重,如式(7)、式(8)所示。该联合算法的具体推导过程可参见文献[13]。

本文基于现场实测数据,根据MODIS 传感器的波段设置,对毛颖等[13]的Kd遥感反演联合算法进行校正,使其适用于MODIS 传感器,进而利用Lee 等[9]的Zsd新理论模型估算南黄海的水体透明度。
2.3 距平计算方法
在后续的时空特征分析中,本文分别计算了4 个子区域水体透明度的距平。由于2002 年和2020 年的水体透明度数据不全,所以计算距平时仅选择了2003–2019 年的数据。具体计算过程为:设2003–2019 年的某子区域i年j月的水体透明度的空间平均值为Mij(i=2003,2004,···,2019;j=1,2,···,12),该子区域2003–2019 年期间j月的平均值Mj计算为
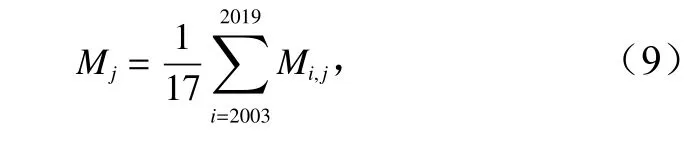
该子区域i年j月的距平DLij则计算为

同理可以计算其他子区域的透明度距平。
2.4 数据资料来源
本研究的现场数据资料采集于2002 年至2003 年间以及2014 年至2016 年间的6 个海上调查航次,调查航次的详细信息及参数测量方法可参见Mao 等[10]和毛颖等[13]的研究。简而言之,本文的数据信息及其用途如表1 所示:其中,数据子集A 的测量参数包括Rrs和Kd,用于校正毛颖等[13]的Kd遥感反演联合算法;数据子集B 的测量参数包括Rrs、Kd和Zsd,用于验证评价耦合毛颖等[13]Kd遥感反演联合算法和Lee 等[9]Zsd新理论模型估算的Zsd的精度。

表1 本研究中现场实测数据的相关信息及用途Table 1 Information of field measured data used in this study
本文所使用的卫星数据主要包括遥感反射率Rrs、海表温度(Sea Surface Temperature,SST)、风速(Wind Speed,WS)、光合有效辐射(Photosynthetic Active Radiation,PAR)以及悬浮颗粒物浓度(Total Suspended Matter,TSM)。其中Rrs、SST 和PAR 均来源于MODIS 的L3 月产品,空间分辨率都为4 km,从https://oceancolor.gsfc.nasa.gov/网站下载获得;WS 数据从https://www.esrl.noaa.gov/网站获得,其空间分辨率为1°×1°。TSM 数据则利用YOC 算法[18]从Rrs数据反演得到。以上数据的时间范围为2002 年7 月至2020 年9 月。
3 结果与讨论
3.1 基于MODIS 数据的水体透明度遥感反演精度
利用本文构建的适用于MODIS 传感器的遥感模型反演Zsd,即先利用优化校正后的毛颖等[13]的遥感反演联合算法反演Kd,再利用Lee 等[9]的新理论模型计算Zsd;然后利用现场实测数据资料对反演结果进行精度检验,本文采用的精度检验指标包括:决定系数R2(Coefficient of Determination)、均方根误差(Root Mean Square Error,RMSE)和平均相对误差绝对值(Mean Absolute Percent Error,MAPE)。RMSE 和MAPE 计算公式为

式中,xi和yi分别表示第i个样本的实测值和估测值;N表示样本数,本研究中N=73。验证结果如图2 所示,可以看出,MODIS 传感器的Zsd遥感模型反演结果与实测数据具有很好的一致性,数据样本较均匀地分布在1∶1 线附近,其中R2、RMSE 和MAPE 分别为0.91,1.69 m 和 25.1%。以上结果表明MODIS 传感器的Zsd遥感模型具有良好的反演精度。

图2 水体透明度(Zsd)遥感反演模型的验证Fig.2 Verification of water transparency (Zsd) remote sensing inversion model
3.2 南黄海水体透明度的时空变化特征
将Zsd的遥感反演模型应用于2002 年7 月至2020年9 月的MODIS 长时序Rrs数据,构建了近20 年南黄海海域每个月的Zsd遥感产品,将Zsd遥感月产品再进行平均得到了南黄海海域的平均Zsd(图3a)。从图中可以看出,南黄海海域的Zsd总体呈现出外海高近岸低的特征。其中,江苏近岸海域Zsd明显低于外海,长江口的Zsd进一步降低,同时长江口的低值区呈现出舌状延伸。为了消除量纲的影响、更好地分析数据的离散程度,计算了Zsd的变异系数(Coefficient of Variation,CV)(图3b)。可以看出,江苏近海以及长江口的CV 值较低,表明这些区域的Zsd变化不大,长期处于较低值;而外海区域的CV 值普遍较高,表明这些区域的Zsd可能存在较大的时间变化。
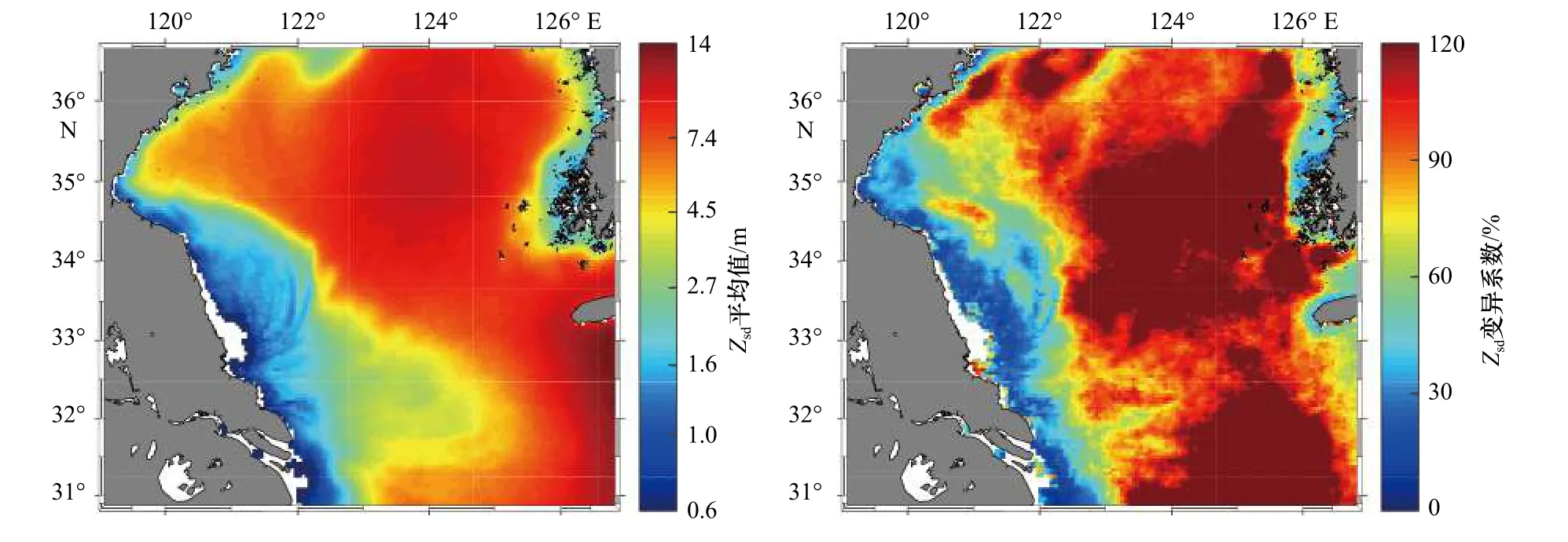
图3 南黄海水体透明度(Zsd)的平均值(a)和变异系数(b)Fig.3 The mean value (a) and coefficient of variation (b) of water transparency (Zsd) in the South Yellow Sea
针对每个月,进一步计算了Zsd所有年份的平均值,并以此分析了南黄海Zsd的时间变化特征,结果如图4 所示,可以看出:整体上在不同月份南黄海海域Zsd都呈现出外海高近岸低的特点,但在不同季节也表现出一定的差异。在冬季(12 月至翌年2 月),外海的Zsd基本处于较低值,随着时间的推移,在夏季(6–8 月)Zsd达到峰值,之后外海的Zsd又逐渐降低,相比之下,近岸的Zsd常年处于低值。以上时间变化特征也使得在冬、春两季(12 月至次年5 月),外海Zsd与近岸Zsd差异远小于夏、秋两季(6–11 月),这种差异在6 月达到最大,在1 月达到最小。
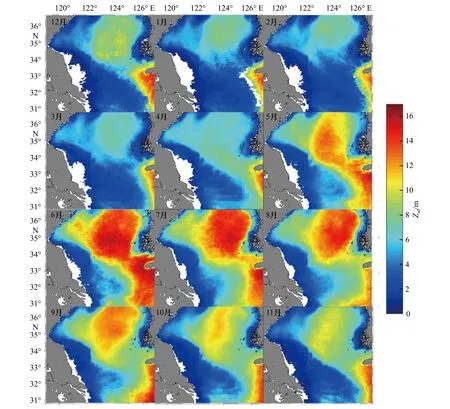
图4 基于MODIS 数据的南黄海水体透明度(Zsd)月变化Fig.4 Monthly distributions of water transparency (Zsd) in the South Yellow Sea derived from MODIS data
对于中国近海水体透明度,学者们也有开展过一定的研究,例如:薛宇欢等[3]利用2006 年和2007 年的中国近海环境调查的透明度数据,分析了中国近海的水体透明度时空分布特征;Mao 等[10]利用2015 年的GOCI 传感器数据,反演分析了渤海、黄海Zsd的日变化和月变化;何贤强等[19]利用1998 年和1999 年的SeaWiFS卫星数据,反演分析了中国近海水体透明度的时空变化规律。虽然这些学者对中国近海水体透明度的时空分布特征做了一定的分析,但其数据仅限于某些年份。相比之下,本文是利用了MODIS 近20 年(2002–2020 年)的数据展开分析研究,长时序的数据资料有利于更深入地挖掘水体透明度的时空分布特征。此外,本文定量计算并深入分析了PAR、SST、TSM 和WS 4 种因子对水体透明度时空变化的影响。
为了更深入地明晰南黄海Zsd的时空变化特征,本文选取了4 个典型区域进行分析,包括南黄海中部(CSYS)、南黄海南部(SSYS)、江苏近海(JC)和长江口(CRE),具体位置如图1 所示。各区域Zsd时间变化结果如图5 所示,可以看出:总体上4 个区域的水体透明度呈现出冬低夏高的变化规律,其中南黄海中部、南黄海南部和江苏近海的Zsd的最大值都出现在夏季,而长江口的Zsd值在夏季却偏低,这可能是由于夏季长江淡水排放达到最大,导致悬浮泥沙增多,进而使得Zsd降低。此外,在不同季节,南黄海中部Zsd值的年际波动比较小,特别是在冬季,Zsd值很稳定。类似地,南黄海南部的Zsd值在冬季的年际波动也很不明显,但在春、夏、秋3 个季节的Zsd值相比南黄海中部的波动要大一些。相比之下,江苏近海和长江口区域的Zsd的年际波动在每个季节都比较大。
为进一步探究南黄海Zsd的长时序变化趋势,本文计算了南黄海中部、南黄海南部、江苏近海和长江口4 个子区域Zsd的距平,结果如图6 所示,可以看出:在南黄海中部、南黄海南部以及长江口的Zsd都呈现出显著性上升趋势(p<0.01),尤其是南黄海中部,可以看出在2018 年以后有着明显的上升趋势。相比之下,江苏近海的Zsd却呈现出显著下降趋势(p<0.01)。

图6 子区域的水体透明度(Zsd)年际变化趋势Fig.6 Annual trends of water transparency (Zsd) of each sub-area
3.3 南黄海透明度变化的影响因素分析
针对南黄海海域的Zsd时空变化特征,本文对其影响因素(4 个子区域)进行了分析探究。本文选取了PAR、SST、TSM 以及WS 4 种环境因素(每月一组数据),分别计算了它们与南黄海中部、南黄海南部、江苏近海和长江口Zsd空间均值的皮尔森相关系数,依此分析了它们对Zsd的影响。由图7 可以看出,PAR和SST 在4 个子区域都与Zsd呈正相关,而TSM 和WS 在4 个子区域都与Zsd呈负相关,而且4 个区域的TSM 与Zsd均呈现出很强的负相关性(相关系数R均大于0.65)。然而,4 个区域Zsd的影响因素也呈现出一定的差异,其中江苏近海和南黄海南部的Zsd受TSM 和PAR 的影响更为强烈,其R值分别为–0.88、–0.86 和0.75、0.61,而南黄海中部则主要受TSM 与SST 的影响,R值分别为–0.93 和0.81;在长江口,TSM 是Zsd影响因素中最大的一个(R=–0.68),相比于PAR、SST 和WS,其R值的绝对值最大相差0.54,最小相差0.31。此外,可以看出在长江口,PAR、SST、TSM 以及WS 4 种环境因子与Zsd的相关性相对于其他区域都要低一些,这可能是因为影响长江口Zsd的变化因素复杂多变,对于其具体原因仍需进一步的研究。
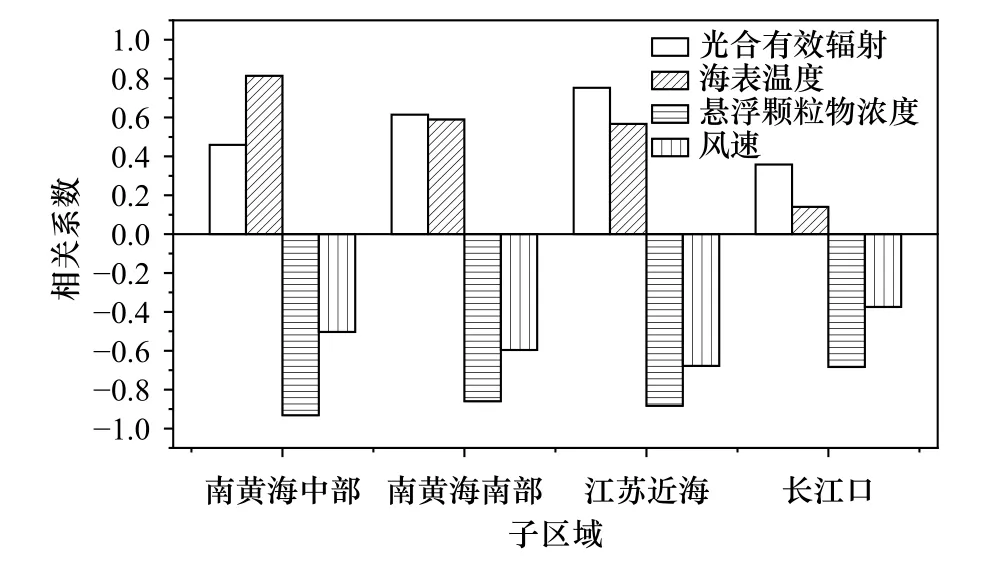
图7 各子区域Zsd 与光合有效辐射、海表温度、悬浮颗粒物浓度以及风速的相关关系Fig.7 Correlation coefficients of Zsd with photosynthetic active radiation,sea surface temperature,total suspended matter and wind speed
在夏季,由于太阳辐射强度最大,使得SST升高,导致表层海水密度小于底层海水密度,上下层海水不能有效混合使得海水出现层化现象[20],海中悬浮物沉积,上层海水TSM 降低,进而导致Zsd增大;在秋季,太阳辐射逐渐减弱,SST 降低,水体层化现象逐渐减弱,海水混合逐渐增强,Zsd分布情况向冬季过渡;到冬季时,太阳辐射达到最低,SST 最小,此时上下层水体的密度差减小,又因为盛行季风的作用海水上下混合强烈,水体层化现象消失,并且风速越大,混合越强烈[21],这个过程使得上层海水的TSM 升高,导致Zsd很低;在春季,太阳辐射逐渐增强,SST 升高,WS迅速减弱,海水混合减弱,水体层化增强,使得Zsd分布特征逐渐开始向夏季过渡。以上环境变化过程使得Zsd与PAR 和SST 呈现出明显的正相关关系,而与WS 和TSM 呈现出明显的负相关关系。此外,为了进一步明晰长江口Zsd的影响因素,本文收集了大通水文站径流量数据以代表长江径流量,将其与长江口洪季的水体透明度做了相关分析,结果发现长江径流量与长江口的Zsd呈现显著负相关性(R=–0.50,p<0.01),表明径流量越大水体透明度越低,这主要是由于径流携带大量悬浮物入海[22–24],降低了水体透明度。
4 结论
通过本文的相关研究,得到了以下几点重要结论:
(1)在空间上,南黄海水体透明度Zsd呈现外海高近岸低的特点,从季节变化来看,南黄海中部、南黄海南部和江苏近海Zsd均呈现出冬低夏高的特点,但对于长江口,夏季的Zsd相对较低,可能与长江淡水排放量在夏季达到最大有关。
(2)近20 年来,南黄海中部、南黄海南部和长江口的Zsd基本呈上升趋势,而江苏近海的Zsd却表现出下降趋势。
(3)整体上,南黄海Zsd与PAR 和SST 呈正相关关系,而与TSM 和WS 呈负相关,相比之下,TSM 是Zsd的最主要驱动因素。
本研究分析了南黄海海域Zsd的时空变化特征及其影响因素,这为南黄海海域的海洋生态环境、区域海洋学等相关研究提供了一定的科学参考。对于Zsd时空变化的驱动因素分析中,本研究仅做了自然环境影响因素的分析。然而对于江苏近海,Zsd可能受到人类活动的影响,针对该问题,仍需在下一步工作中结合人类活动数据资料进行深入分析研究。

