基于SAR 多普勒质心频移的海面流场迭代反演算法
秦艳萍,范陈清,张玉滨*
(1.中国海洋大学 信息科学与工程学院,山东 青岛 266100;2.自然资源部第一海洋研究所,山东 青岛 266061)
1 引言
海流是海洋重要的运动形式之一,与海上污染物的扩散、海上军事活动、水产养殖和全球气候变化等密切相关[1],所以研究其特征和变化规律具有重要的科学意义。遥感技术的快速发展使得大范围、高精度的探测海洋信息成为可能[2]。目前,利用遥感技术反演海流的方法主要有光学遥感和微波遥感。光学遥感主要是根据示踪物(叶绿素等)的位移时间关系来反演流速,其易受天气的影响[3–4];微波遥感不受天气的影响,其海流反演手段主要有:高度计[5]、地波雷达[6–7]、多普勒雷达散射计[8–11]、合成孔径雷达(Synthetic Aperture Radar,SAR)[12–16]等。高度计反演海流覆盖范围广,但其流场产品分辨率较低,不适合小尺度海流的测量[5];地波雷达虽具有反演分辨率高、全天候等优势[6],但其主要是岸基测量,覆盖区域有限;多普勒雷达散射计可实现二维测流[8],但因为其是真实孔径雷达,流场产品分辨率较低;而合成孔径雷达则具有高分辨率、全天候、全天时等优势[12],使其成为反演海流的新手段。目前,利用SAR 技术反演海流主要有两种方法:顺轨干涉(Along-Track Interferometry,ATI)法和多普勒质心频移(Doppler Centroid Anomaly,DCA)法。顺轨干涉法基于两幅沿轨天线分别获得的SAR 复图像的相位差反演流场[17];多普勒质心频移法则根据海表层运动产生的多普勒质心频移与其径向速度的关系反演海表面流速[18–21]。相比DCA 方法,ATI 技术反演精度、分辨率更高[22],但其成像条件苛刻,数据不易获取,所以不具有普适性。虽然DCA 方法流速产品分辨率较低,但其适用数据丰富且容易获取,如Radarsat-2、Envisat ASAR 和Sentinel-1 等数据都可用于DCA 方法反演海面流场,具有业务化观测全球海洋表面流的潜力。
DCA 方法中由多普勒质心频率异常反演的地距多普勒速度不仅与海表面流场有关还与海表面风场有关。2004 年Chapron 等[21]利用Envisat ASAR 数据分析了全球海洋多普勒测量数据,发现多普勒频移与海面风场有很高的相关性;后来Chapron 等[23]又利用Envisat ASAR 数据基于多普勒质心频率异常提出了一种简单的模型:UD≈γU10+UC(γ为风贡献因子),以表示海面风场和流场对多普勒速度的影响,并发现当入射角为23°且在中风和海态完全发育时,风贡献因子 γ=0.3。国内学者在基于DCA 法反演海面流场并去除风场影响方面也做了大量研究。杨小波[24]利用多普勒质心频移法反演海流时,分析了海表面风场对流场反演的影响,发现风对流场的分布和结构有一定的影响,并给出了SAR 成像时刻研究区域风场产生多普勒速度的关系式:UDW=0.03U10;侯富城等[12]利用多普勒质心频移法提取了内波产生的海表面流,并基于Chapron 等[23]提出的模型,指出在中等风速下,风贡献因子 γ取值为0.2~0.25。虽然Chapron 等[23]提出的模型给出了风场和多普勒速度的关系,可以很好地修正风场产生的反演误差,但只给出了风贡献因子 γ在特定雷达频率、入射角下的经验值。风贡献因子 γ与雷达频率、入射角以及雷达天线的偏航角等多个参数有关[23],一般不能由简单的线性关系描述,并且对流场反演结果的精度影响很大,所以需找到正确估算风贡献因子 γ的方法,以提高流场反演精度。
针对以上反演过程中去除风场影响存在的问题,本文提出了一种基于M4S 模型的迭代方法,用于流场反演。M4S 是由德国科学家Romeiser 等[25]开发的海面微波成像仿真模型,其核心程序模块主要包括海表面微尺度波波高谱计算模块和雷达海面成像仿真模块。在给定风场和流场的情况下,可仿真海浪谱、海面SAR 复图像(强度、相位)以及多普勒谱等信息。因此,基于M4S 模型并结合弦截下山法可估算并去除风场的影响,反演海面径向流速。首先利用频谱拟合法从SAR 原始复数据中获得实测多普勒中心频率;再利用SAR 数据头文件信息估算卫星和地球表面的相对运动产生的预测多普勒中心频率,继而得到多普勒质心频率异常值并将其转换为地距多普勒速度;然后基于M4S 模型,利用本文提出的弦截下山法迭代反演SAR 局部区域的流场,估算风场对多普勒速度的影响,继而反演整幅SAR 图像的海面径向流速;最后通过与实测海面流场数据比对,验证反演算法的有效性。
2 数据源
本文采用的实测海表流场数据和SAR 数据来自作者课题组组织的星地匹配实验,用安德拉海流计现场采集海表流场数据,并与Radarsat-2 SAR 卫星数据作时空匹配。采用安德拉海流计测量海表面流时,将海流计悬挂于浮体之下,使其处于海表面以下约0.4 m处,在船只停航时,用绳子牵住浮体,并在船尾将浮体和海流计放置于离船200 m 的海面,记录停止放绳的时间和收绳的时间,此时间段内为有效数据。所用安德拉海流计型号为SEAGUARD,这是一种自记录海流计,具有二维流场测量能力,测量流速的分辨率为0.1 mm/s,平均误差为±0.15 cm/s,测量流向的分辨率为0.01°,误差为±5°。现场测量海表面流时,实验海流计位于海表面以下约0.4 m 处,测量的是近表面流速,通过SAR 数据测量得到的流速是海表层流速。因为两者测量的深度基本匹配,所以可用此实验海流计所测的实测流场数据对SAR 数据的流场反演精度进行验证。
采用的SAR 数据源于Radarsat-2 卫星,为标准成像模式下的单视复数据。结合星地匹配实验中现场实测数据的位置及时间信息,本文选用了两幅Radarsat-2 SAR 图像进行流场反演,其UTC 时间分别为2019 年6 月23 日21 时53 分和2019 年6 月25 日10 时11 分。数据信息如表1 所示,SAR 数据覆盖区域如图1 所示。SAR 覆盖区域内,海表面流即包括有一定规律性的地转流和潮流,也包括无规律的风生流,所以整体来说该区域的海表面流场分布无明显规律。
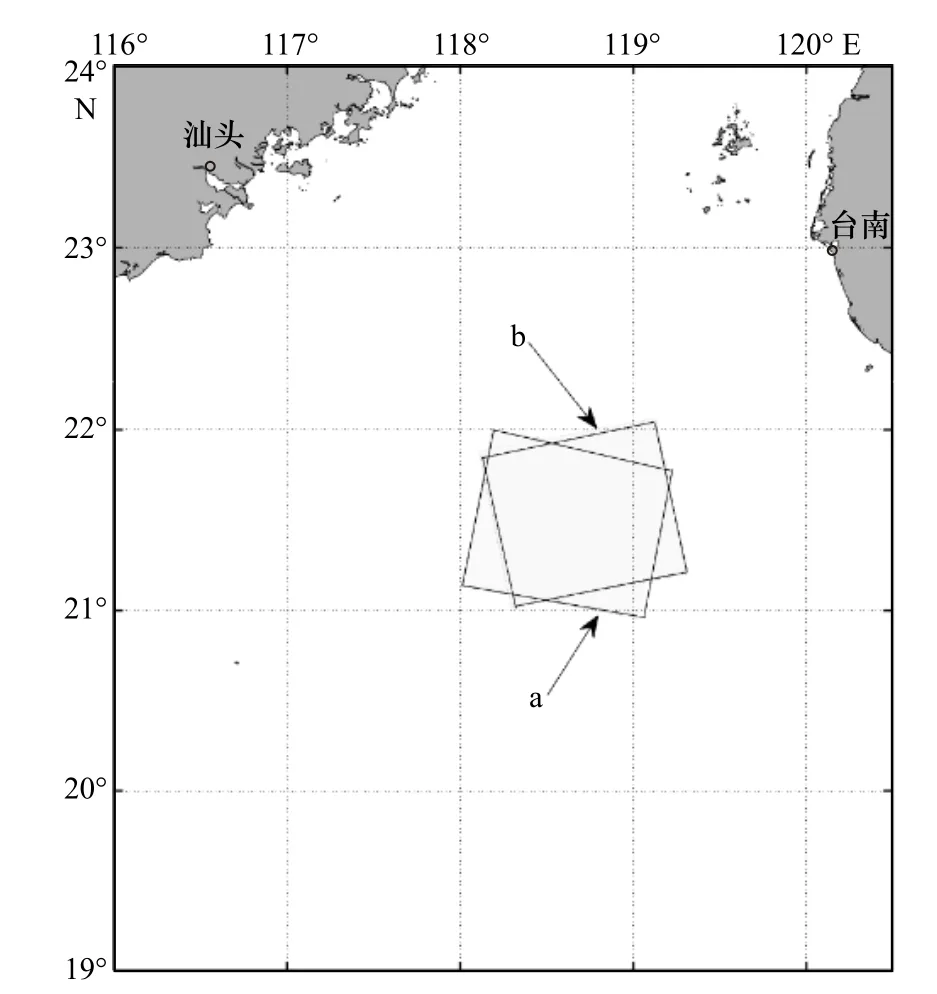
图1 所用Radarsat-2 SAR 数据覆盖区域Fig.1 Coverage area of Radarsat-2 SAR data

表1 本文所用Radarsat-2 SAR 数据信息Table 1 Radarsat-2 SAR data information used in this paper
风场数据采用欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts,ECMWF)ERA5 中的再分析风场数据。数据中包括海面上空10 m处风场的东向分量、北向分量和经纬度、时间信息,其空间分辨率为0.25°×0.25°,时间分辨率为1 h。在使用该风场数据时发现其时空分辨率比反演得到的SAR流速产品分辨率小,无法直接使用,所以本文通过时空插值使其与SAR 流速产品匹配,以方便之后的处理。
3 模型与方法
3.1 基于多普勒质心频率异常的多普勒速度估算方法
从SAR 实测数据估算的多普勒中心频率称作实测多普勒中心频率,主要包含卫星和地球表面的相对运动导致的多普勒频移与海面水质点运动导致的多普勒频移。实测多普勒中心频率的估计方法有基于幅度的频谱拟合法和基于相位的相位增量法[26–27]。本文利用频谱拟合法从SAR 复数据中估计实测多普勒中心频率。首先选取一定大小的窗口,对该窗口内的数据进行快速傅里叶变换(FFT)。然后在得到的方位向能量谱中找到多普勒中心频率。由于直接从方位向能量谱中寻找多普勒中心频率较为困难,本文结合能量均衡法,将方位向功率谱与参考函数相关,寻找相关后的过0 点,并把过0 点处的频率作为该窗口的多普勒中心频率[28]。最后以一定的步长移动窗口得到整幅SAR 图像的多普勒中心频率。
卫星和地球表面的相对运动产生的多普勒中心频率称作预测多普勒中心频率,其计算方法主要有两种:第一种方法基于卫星姿态和速度等参数,利用几何关系估算该多普勒中心频率;第二种方法从元数据中读取多普勒系数、斜距时间、标准斜距时间等数据估算预测多普勒中心频率。由于Envisat ASAR、Radarsat-2 等卫星,SAR 原始数据处理时已经估算了预测多普勒中心频率,并给出了拟合多项式,所以本文基于第二种方法估算预测多普勒中心频率,表达式为[29]

式 中,dopcoef1、dopcoef2、dopcoef3、dopcoef4、dopcoef5为多普勒系数;t为斜距时间;t0为标准斜距时间。
将卫星和地球表面的相对运动产生的预测多普勒中心频率从实测多普勒中心频率中去除之后得到的剩余频率称作多普勒质心频率异常[30]

式中,fDc为实测多普勒中心频率。经过式(2)的运算,卫星相对地球表面的运动效应被去除,因此多普勒质心频率异常对应的只是海面水质点的运动速度。将多普勒质心频率异常转化为径向多普勒速度,再将其投影到地表局部切平面坐标系得到地距多普勒速度
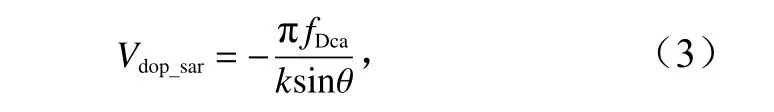
式中,k为雷达电磁波波数;θ为雷达入射角。
上述计算得到的地距多普勒速度对应海面水质点运动,该运动主要包括海表面流场、海浪轨道速度等,其中海浪受到海表面风场的调制作用,即风场可间接影响多普勒速度。Chapron 等[23]提出的多普勒模型通过波浪谱表示了风对多普勒速度的影响,并给出了计算风场和流场产生的多普勒速度的经验表达式。
3.2 海面流场反演的弦截下山法
3.1 节获得的地距多普勒速度中既包含了流场的贡献又包含了风场的贡献,只有准确去除风场的贡献,才能获得海面流场。利用M4S 模型仿真的多普勒谱信息可以计算多普勒质心偏移,进而获得M4S模拟的多普勒速度场Vdop_m4s,即

当输入M4S 模型的风场UW和流场UC信 息与真实SAR 成像时海面的风场和流场信息一致时,在忽略M4S 模型建模误差的条件下,M4S 模拟的多普勒速度Vdop_m4s应与从真实SAR 图像反演的多普勒速度Vdop_sar相等,即Vdop_m4s=Vdop_sar。在基于多普勒质心频移法获得了真实SAR 图像反演的多普勒速度Vdop_sar的条件下,通过M4S 模型获得海面真实流场,也就是求解以下关于海面流场UC的方程(假设海面真实风场UW已知)

上述方程是关于海面流场UC的 非线性方程,通过求解此方程可以获得与SAR 图像对应的海面流场。
这里采用迭代方法求解式(5),为了兼顾计算速度与迭代收敛性,选择弦截法并结合下山法进行求解。弦截法不需要求解函数f(UC)的导数,容易实现;而下山法可以在一定程度上保证迭代的收敛性。弦截法求解非线性方程f(UC)=0的迭代公式为[31]

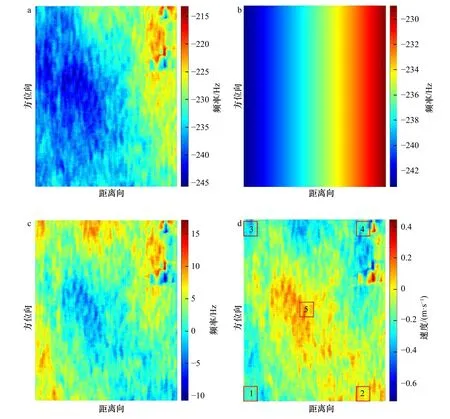
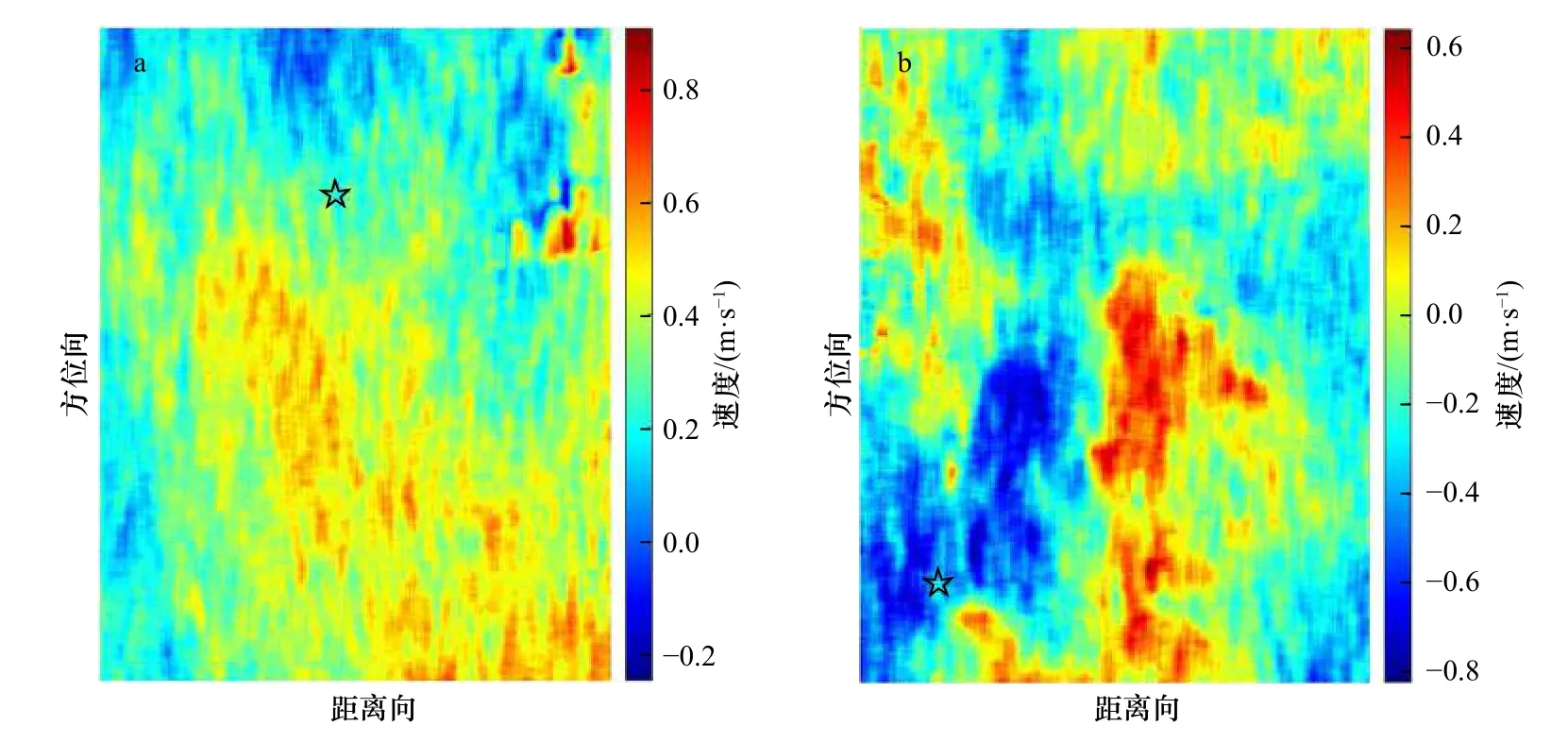
式中,Uk−1、Uk和Uk+1分 别表示第k−1、k和k+1次迭代的流速近似解。运算中需要首先把两个初猜值U0和U1代入式(6),开启迭代运算,直到相邻两次迭代的结果满足 |Uk+1−Uk| Uk+1、Uk为了满足上述下山条件,在式(6)中引入下山因子A,其形式变为 下山因子A的取值为,···,直到使得下山条件式(7)成立为止。 基于M4S 模型,采用上述弦截下山法迭代反演流场的流程如图2 所示,具体计算按如下步骤。 图2 弦截下山法迭代反演流场流程Fig.2 Flow chart of iterative retrieval of current field by secant downhill method (1)基于SAR 反演的海面多普勒速度Vdop_sar设置迭代初猜值,弦截法需要两个初猜值,这里将Vdop_sar作为U0,U0+V′(V′=±0.1)作 为U1,并将其输入M4S 模型,获得V0dop_m4s、V1dop_m4s,在上述4 个值以及风场、初始化参数k、A的基础上,开启迭代运算。 (2)将由式(5)获得的f(Uk)和f(Uk−1)的绝对值进行比较,如果满足下山条件|f(Uk)|<|f(Uk−1)|则进入第(3)步处理,反之,进入第(4)步处理(当k=1时,通过选择不同的V′的 值,使得 |f(U1)|<|f(U0)|成立)。 (3)利用式(6)计算非线性方程(5)新的近似解Uk+1,判断 |Uk+1−Uk|是否满足误差阈值条件,满足则停止迭代,以Uk+1作为最终的流场;若不满足误差阈值条件,将Uk+1输 入M4S 模型获得Vk+1dop_m4s,更新迭代参数k=k+1,A=1,转入第(5)步操作。 (4)下山因子减半A=A/2,采用式(8)基于Uk−2和Uk−1重新计算Uk,判断 |Uk−Uk−1|是否满足误差阈值条件,满足则停止迭代,以Uk作为最终的流场;若不满足误差阈值条件,将新的Uk输 入M4S 模型获得新的Vkdop_m4s,转入第(5)步操作。 (5)基于更新的Uk−1、Uk及Vk−1dop_m4s、Vkdop_m4s,转入第(2)步,进行下一步迭代运算。 由于M4S 模拟仿真过程计算量较大,3.2 节的弦截下山法一般只适用于SAR 图像局部区域的流场反演。对于整幅SAR 图像,可以通过分块迭代计算海面流场,估算每块区域的风贡献因子 γ,进而估算整幅SAR 图像的风贡献因子 γ。本文将从整幅SAR 图像上均匀的选取大小相等的几个局部区域(本文中是5 个),利用3.2 节提到的方法分别迭代反演其流场。将迭代反演获得的流场、相应SAR 图像反演的多普勒速度Vdop_sar以及外部风场数据(ECMWF 风场数据)代入式(9),获得每个局部区域的风贡献因子 γ。 由于风贡献因子 γ与雷达频率、入射角以及雷达天线的偏航角等因素有关[23],而在一幅SAR 图像中这些参数基本保持不变,所以本文中将各局部区域的风贡献因子 γ的平均值作为整幅SAR 图像的风贡献因子γ。 采用3.1 节描述的方法,对两幅Radarsat-2 SAR 数据进行处理,结果如图3 和图4 所示。从图3 中可以发现,相比于预测多普勒中心频率,多普勒质心频率异常要小的多,这是由于两者产生的原因不同,预测多普勒中心频率由卫星和地球相对运动产生,而多普勒质心频率异常由海表层运动产生。 经上述处理获得的地距多普勒速度(图3d、图4)中即包含了流场贡献又包含了风场贡献,文献[23]表明风场的贡献甚至更大一些,因此只有准确的去除风场的贡献,才能获得最终的海面流场。这里首先采用3.2 节提出的弦截下山法对从SAR 图像中截取的小区域进行迭代计算,获得其海面流场。例如,对2019 年6 月23 日SAR 图像反演的地距多普勒速度分布图(图3d)中红框1 所示局部区域(大小为方位向5 km×距离向6 km)进行迭代计算,计算3 次的误差|Uk+1−Uk|依次是0.34 m/s、0.07 m/s、0.02 m/s,已经满足误差阈值条件(e<0.05 m/s),因此停止迭代,输出最终流场。然后,将该流场和相应SAR 图像反演的多普勒速度Vdop_sar及风场数据代入式(9)估算该局部区域的风贡献因子 γ,得到图3d 中红框1 区域的风贡献因子 γ为0.15。用同样的方法估算其他局部区域的风贡献因子 γ,并将所有的风贡献因子 γ进行平均,得到整幅SAR图像的风贡献因子γ。2019 年6 月23 日SAR 图像的平均风贡献因子 γ为0.15,2019 年6 月25 日SAR图像的平均风贡献因子 γ为0.22。将两幅SAR 图像的平均风贡献因子 γ分别代入式(9)计算风场产生的多普勒速度,并将其从地距多普勒速度Vdop_sar中去除,得到整幅SAR 图像的海面径向流速,如图5 所示。对SAR 地距多普勒速度图中局部区域进行迭代计算时,通常只需迭代两三次就可以满足误差阈值条件,获得该区域的径向流速。该结果表明本文提出的弦截下山法具有良好的收敛性和较高的收敛速度。 图3 2019 年6 月23 日SAR 图像反演结果Fig.3 SAR image retrieval results on June 23,2019 图4 2019 年6 月25 日SAR 数据反演的地距多普勒速度Vdop_carFig.4 Ground range Doppler velocity retrieved from SAR data on June 25,2019 为了验证本文方法,把SAR 反演的海表面径向流速与星地匹配实验中安德拉海流计采集的流场实测数据比对。安德拉海流计是常用的海流测量仪器,能够准确测量海水瞬时速度。实验中将海流计悬挂于浮体之下,使其处于海表面以下约0.4 m 处,保证其测量的是近表面海水的速度。获取海表流场需要对海流计所测时间序列的速度取平均,以去除海浪的速度贡献。将星地匹配实验中测得的实测数据与SAR 图像进行时空匹配,得到两个实测数据分别与两幅SAR 数据对应,具体数据如表2 所示,表中的流速、流向是卫星过境时刻前后10 min 内的平均值。 由于SAR DCA 方法反演的流速是一维径向流速,在将海流计测得的流场与其比较时,需要将海流计所测二维流场向SAR 径向作投影。2019 年6 月23 日雷达视向角为279.93°,2019 年6 月25 日雷达视向角为79.63°。将与之匹配的海流计所测流速分别投影到SAR 径向,得到实测径向流速分别为0.23 m/s、–0.14 m/s(如表2 中最后一列所示)。在SAR 反演的径向流速分布图中寻找实测数据的匹配位置点,如图5a 和图5b 中黑色五角星所示,以该点为中心,1 km×1 km 范围内对SAR 反演的径向流速取平均,得到两幅SAR 图像DCA 方法反演的流速分别为0.19 m/s,–0.29 m/s。将DCA 法反演的径向流速与实测的径向流速进行比较,得到两幅SAR 图像在实测点处的反演误差分别为0.04 m/s 和0.15 m/s。在比对实验中,SAR反演结果的精度与产品分辨率之间往往存在矛盾。平均范围越大流速精度越高而分辨率会越低,反之,则流速精度越低而分辨率越高。所以需在两者之间进行权衡,本文在1 km×1 km 的范围内取平均,可在相对较高的分辨率(1 km×1 km)下获得较高的精度。 表2 海流计实测海流数据Table 2 Current data measured by ocean current meters 图5 两景SAR 数据对应的海表面径向流速Fig.5 The radial velocity of the sea surface corresponding to the SAR data of the two scenes 为了克服SAR 复图像DCA 方法反演海面流场时风场贡献去除困难的难题,本文提出了基于M4S 模型的弦截下山法迭代反演海面流场。首先采用传统的DCA 方法反演海面多普勒速度;然后采用本文提出的弦截下山法,迭代反演SAR 地距多普勒速度分布图中局部区域的海面流场,并估算其风贡献因子γ;最后对不同局部区域的风贡献因子 γ取平均,获得整幅SAR 地距多普勒速度分布图的风贡献因子 γ。进而去除风场对多普勒速度的贡献,获得整幅SAR 图像对应的海面径向流速。将两幅SAR 图像的反演结果与实测近海表面流速进行比对,得到的反演海面径向流速偏差分别为0.04 m/s 和0.15 m/s。研究结果表明,本文提出的弦截下山法不仅具有良好的收敛性和较高的收敛速度,而且对于本文使用的两景SAR 数据,反演的海面径向流速偏差在0.2 m/s 内。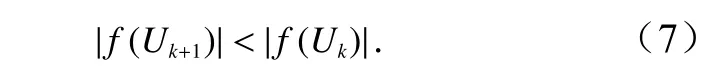


3.3 风贡献因子 γ的估算方法

4 结果与精度验证
4.1 反演结果

4.2 精度验证

5 总结

