莱州湾南岸海水入侵特征及基于WA-NARX 混合模型的动态预测

董凡，张晓影，陈广泉,，戴振学，王延诚, 3

(1.吉林大学 建设工程学院，吉林 长春 130026；2.自然资源部第一海洋研究所 自然资源部海岸带科学与综合管理重点实验室，山东 青岛 266061；3.青岛海洋科学与技术试点国家实验室 海洋地质过程与环境功能实验室，山东 青岛 266237)

1 引言

近年来，受气候变化和人类活动的双重影响，全球海岸地区都面临着海水入侵的威胁。海水入侵可引发地下水水质恶化、土壤退化等生态环境问题，严重制约社会的可持续发展[1–4]。科学管理沿海地区地下水，预测近岸地下水位和电导率，掌握地下水位及盐度的动态变化，对合理开发利用海岸带地下水资源，防止海水入侵加剧，保护海岸带生态环境有十分重要的指导意义。然而，受自然条件和人为因素的影响，海水入侵在时间序列上表现出时空性、不确定性及动态变化等特性，多种因素对海水入侵的影响并非多因子影响的线性叠加，从而使预测海水入侵的演化过程变得十分困难。

随着人工智能的兴起，由于人工神经网络（ANN）可以较好地映射非线性变化，因此被广泛应用在水文变量预测中。其中BP 神经网络模型的应用范围最广[5]，但其神经网络训练的时间长，收敛速度慢，输入信号由输入层单向传递给输出层，网络模型只能使用有限步的历史信息。而循环神经网络（RNN）凭借其循环结构的特点，通过反馈连接可以使用长期的历史信息，因此更加适合时间序列的预测[6]。具有外部输入的非线性自回归神经网络（Nonlinear Autoregressive Models with Exogenous Inputs，NARX）作为循环神经网络的一种，在地下水位的预测研究领域备受青睐。Guzman 等[7]使用NARX 模型预测密西西比河流域含水层，Wunsch 等[8]运用NARX 模型预测德国西南部数口井的地下水水位，Di Nunno 和Granata[9]应用NARX网络预测位于普利亚地区的76 口监测井的日地下水水位。研究结果表明，NARX 神经网络在预测时间序列上具有显著优势。

尽管ANN 在时间序列预测方面应用广泛，具有灵活性，但是如果不对输入和输出数据进行预处理，它可能无法处理非平稳数据[10–11]。小波变换作为一种数据预处理技术，可以将非平稳时间序列的小波分解成不同的尺度，提供对序列结构的解释，并仅用几个系数来提取有关其历史的重要信息。该技术被广泛应用于非平稳信号的时间序列分析[12]，通过将非平稳信号分解成不同时间水平的子信号，可以较好地预测非平稳信号[13–18]。将小波变换和人工神经网络模型相结合，发挥这两种模型的优势，可以明显提高预测精度，增加有效预测时段。目前，混合模型已广泛应用于部分水文要素的预测，如降雨、径流和蒸发[19]。张建峰等[20]建立小波–BP 神经网络的混合模型预测华北平原城市地下水位。Seo 等[21]将小波分析（WA）分别结合BP 神经网络、自适应神经模糊推理系统，预测水库水位并对结果进行对比。Zhang 等[22]构建了小波分析和NARX 神经网络混合模型对舟山填海区地下水位进行预测，预测精度较高。

由于受全新世海侵、气候干旱、海平面上升以及不合理的人类活动的影响，莱州湾地区是我国海水入侵灾害最为严重和典型的地区[23]。近年来，在上述因素综合影响下，莱州湾地区地下咸水体分布面积已超过22 000 km2[24]，严重污染地下淡水资源，土壤次生盐渍化面积不断扩大，对海岸带区域的工农业生产和生态环境造成严重影响，海水入侵已成为该地区严重的环境问题之一，严重制约经济社会发展。因此，开展莱州湾地区海水入侵动态特征分析，建立预测模型，对提高海岸带地区防灾减灾能力和经济、社会可持续发展具有重要意义。在本研究选择莱州湾南岸典型监测剖面，首先分析地下水位和地下水电导率的动态变化特征，分析对比不同输入参数对模型预测精度的影响，建立基于WA-NARX 混合的海水入侵预测模型，对近岸地下水位和电导率进行预测模拟，研究结果可为海岸带海水入侵的实时监测、预测、预警提供理论与技术支撑。

2 研究区与研究方法

2.1 研究区与资料

2.1.1 研究区概况

研究区位于莱州湾南部（图1），潍坊北部的滨海区。研究区内设有6 口监测井（BH01–BH06），分别沿垂直于海岸带的剖面由靠近海岸带的监测井BH06 向内陆的监测井BH01 方向分布。研究收集了降雨、蒸发、潮汐、电导率、地下水位和农业排灌用电量数据，见图2。其中，潮汐的变化是潮位站监测的海水位每小时的变化，降雨量与蒸发量是日测数据，排灌用电量是研究区每小时灌溉所用电量。研究选 取2011 年10 月1 日 至2012 年10 月31 之 间 的 监测数据作为研究对象。

图1 研究区位置图及监测井分布Fig.1 Location of the study area and monitoring wells

图2 各影响因素时间序列Fig.2 Time series of influencing factors

2.1.2 研究区水文地质特征

莱州湾南岸地区属于鲁北平原水文地质区、潍北滨海平原水文地质亚区。该地区地表水系较发达，地下水水文地质特征在水平和垂向上均变化明显。地貌类型由南向北依次为山前冲洪积平原、冲积海积平原和滨海海积平原，海岸类型为粉砂淤泥质海岸。此处的冲洪积平原由多个扇缘相互交接的冲洪积扇群组成，冲洪积平原的前缘被海积物或黄河冲积物所掩埋，含水层厚度大、颗粒粗，具有多层结构。含水层颗粒自上而下呈现由粗变细的趋势，而在水平方向上则具有冲洪积扇的水文地质特征[25]。

如图3 所示，研究区普遍存在一层中更新统砂质黏土弱透水层，埋深一般为 40～70 m，层厚约20 m。有3 层海侵层，分别对应晚更新世以来发生的3 次大海侵。在3 次海侵中都滞留了浓缩于地层中的古海水（咸–卤水），与淡水含水层在水平方向上相连，是该区咸–卤水入侵的来源，主要出现在晚更新世和全新世地层中。

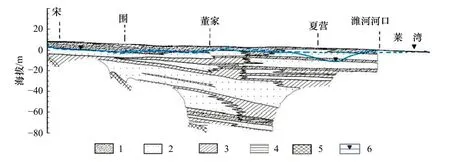
图3 研究区剖面图（修改自文献[26]）Fig.3 Hydrogeology of the cross section from south to north in the study area (modified from reference [26])

2.2 研究方法

2.2.1 小波分析

在本研究中，运用小波分析的方法来识别显著的振荡周期，从原始数据中提取有用的信息，并将这些信息分解成一系列小波函数，小波函数由母波函数生成。本文采用的母波函数是Morlet 小波：

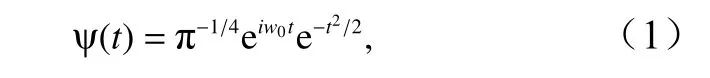
式中，w0为无量纲频率；t为时间。通常，选择w0=6的Morlet 小波[27–28]。连续小波变换（CWT）用于识别信号在时频域的主振荡。连续小波变换的f(t)如下所示：

式中，a为尺度或频率参数；b为时间或位移参数;(t) 是 复共轭函数 ψ(t)。由式（2）可知，小波变换在不同分辨率或尺度下呈现出不规则和不对称的特点，将f(t)分解为一系列低分辨率分量。

在实际应用中，连续小波变换常被离散小波变换（DWT）所代替。令a0>1,b0∈R,k和j为整数，则f(t)的离散小波变换可表示为

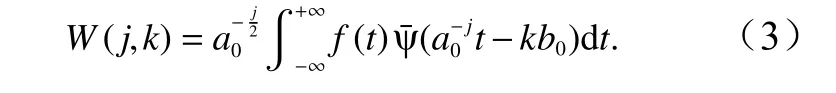
在式（3）中，参数a0和b0最常用的选择是使用对数缩放[29]，即a0=2,b0=1。原始时间序列在频率（a或j）和时间（b或k）域的特征被连续小波变换的W(a,b)或离散小波变换的W(j,k)所反映。

将经典的连续小波转换为离散小波有多种算法，如Mallat 算法和á Trous 算法。本文采用了á Trous 算法[30]。á Trous 的分解算法定义如下：

式中，g(n)为离散低通滤波器；Ci(t) 和Wi(t) (i=1,2,···)分别是分辨率为i级的尺度系数和小波系数。W1(t),W2(t),···,Wp(t) 和Cp(t)组成分辨率为P的离散小波变换。

在小波分析中经常使用近似特征和细节分量，近似特征表示信号的低尺度，即低频信息；细节分量表示信号的高尺度，即高频信息。离散小波变换使用低通滤波器g(n)和高通滤波器h(n)将f(t)分解成不同尺度上的低频成分（C1，C2，C3··· ）和高频成分（W1，W2，W3···）。因此，f(t)可以分解为包含其近似分量（低频成分）和细节分量（高频成分）。高频信号捕获原始时间序列数据中的小尺度特征，见图4 小波分解部分。

图4 WA-NARX 模型建模流程Fig.4 Flow chart of WA-NARX neural network hybrid model

2.2.2 NARX 神经网络

NARX 神经网络是一种有外部输入的非线性自回归网络模型[31]，表示为

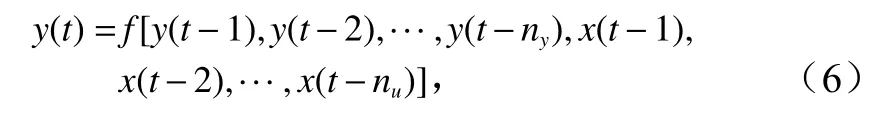
式中，y(t)代表输出信号；x(t)代表外部输入信号；f为非线性函数。即输出信号y(t)可由输出信号前ny个值和外部输入信号x(t)前nu个值通过f非线性映射得到。

NARX 神经网络由网络的输出反馈和动态的神经元构成，是一种动态神经网络。它的结构清晰，通常包含输入层、输出层、隐含层及输入延时和输出延时这些网络结构（图5）。NARX 神经网络具有开环和闭环两种模式，闭环网络可以进行多步预测。与一般神经网络相比，NARX 神经网络的反馈结构和梯度下降算法使其拥有更好的收敛速度和学习效率，是一种研究较为广泛的动态神经网络[32–33]，因此，NARX 神经网络既可以用于时间序列建模，也可以用于非线性滤波[34]。

图5 输入到输出的NARX 神经网络结构Fig.5 Nonlinear auto-regression with exogenous input NARX

2.2.3 小波与NARX 混合模型

WA-NARX 混合模型是利用多分辨率小波分解得到的子时间序列作为输入的NARX 模型。利用小波变换将原始信号依次分解成不同尺度上的信号成分，á Trous 算法产生低频的近似分量（C）和高频的细节分量（W）[35]。本研究利用L=int来确定小波的分解层数[36]，其中L表示小波层的个数，n表示时间序列中的数据点个数，int[ ]为取整函数。研究所包含时间序列的数据点个数为9 528，经计算需要4 个分辨率级别。

本研究中，利用á Trous 算法首先将水位、潮汐和降雨等参数的小时时间序列分解为一定数量的子时间分量。根据潮汐水位随时间的变化规律，运用小波分析的方法来识别显著的振荡周期，并从原始数据中提取潮汐水位变化的近似特征值和细节分量，然后将时间分量作为混合模型的输入。选择最重要的时间分量作为输入，这些时间分量与原始数据具有很高的相关性。为了判别预测的准确性，本文将均方根误差（RMSE）和拟合度（R2）作为性能指标来衡量模型的预测精度。同时，利用matlab 中的perform 函数结合网络结构与均方误差（MSE）计算网络性能来评价网络的学习及预测能力。

WA-NARX 混合模型在建模过程中，数据被分为两个子集：训练集和测试集。训练数据集（75%）用于优化网络配置，测试数据集（25%）用于测试网络性能。此外，WA-NARX 混合模型的隐含层神经元数是通过反复试验确定的。在本次研究中，最终确定10 个隐含层神经元。WA-NARX 模型建模流程见图4，如图所示：首先是参数和样本的选择，利用小波变换将原始时间序列分解成不同信号成分的小波分量，然后将分解的小波分量输入到NARX 神经网络模型中进行训练预测，最终得到预测结果。

3 结果和讨论

3.1 海水入侵动态变化特征

3.1.1 地下水位动态变化特征

根据研究区监测井2011–2012 年间的地下水水位监测数据，结合研究区内相应时段的降雨量绘制监测点的地下水位动态变化曲线（图6）。根据研究区2011–2012 年各监测井采集的地下水位动态数据，计算各监测井地下水位的最大值、最小值、平均值以及标准差等空间变化统计特征，计算结果见表1。图6 显示，各监测井地下水位的变化趋势基本一致。监测井在2011–2012 年间的地下水位的变幅为1.175～4.358 m，各监测井地下水位在2011 年12 月、2012 年4 月、2012 年8 月这3 个时间段内均有突变点，与降雨量变化相对应。在降雨后，多数监测井地下水位有明显上升的趋势。2011 年的11 月份到2012年的2 月份水位逐渐上升后趋于平缓，因降雨补给存在滞后效应，随后水位开始下降，2012 年3–4 月份水位随着降雨上升，在4 月末水位达到全年最高值，因春灌开采影响，5 月份虽有降雨补给，但地下水位也开始下降，7–8 月是降雨最频繁月份，受强降雨的影响，地下水位随降雨量波动变化。在降雨过程中，间歇性的小雨只能湿润土壤表层，不能有效补给地下水；集中式暴雨入渗系数低，大部分转化为地表径流。而连续小雨可以充分入渗到地下，因此有利于地下水补给[37]。可以判断监测井2011–2012 年地下水年内动态变化特征为降雨入渗–开采型。

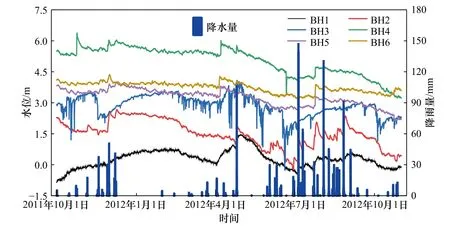
图6 监测井2011–2012 年间地下水位变化曲线Fig.6 Groundwater level variation in monitoring wells from 2011 to 2012

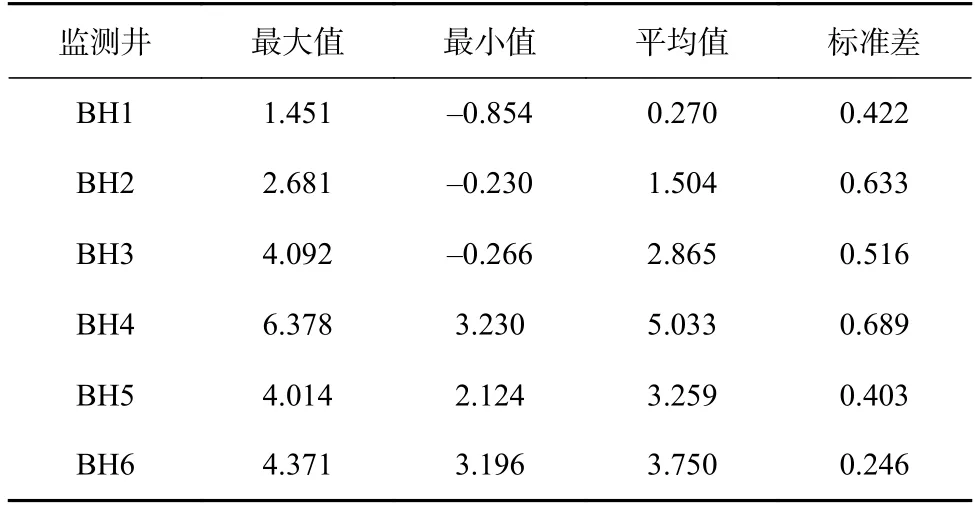
表1 监测井地下水位统计特征分析（单位：m）Table 1 Analysis on statistical characteristics of groundwater level in monitoring wells (unit:m)

地下水超采是海水入侵最直接的原因，地下水位的持续下降会破坏水压力平衡，当沿海含水层地下水位低于海平面时，就会发生海水入侵，因此在分析区域内海水入侵状况时，可以根据地下水位的动态变化近似推断海水入侵状况。对海水入侵的监测，通常是对地下水中氯化物和矿化度进行分析[38]，也有相关研究[39–40]用电导率替代Cl–作为监测海水入侵的指标，指出水中Cl–含量与电导率成正比。如图7 所示，地下水位和电导率在一定程度上呈负相关，即地下水位下降，电导率上升。当地下水位下降时，淡水入海流量减小，海水入侵加剧，地下水中电导率升高。因此，从图中可以看出地下水位动态变化特征在年内时间尺度可较为准确表征海水入侵的变化。

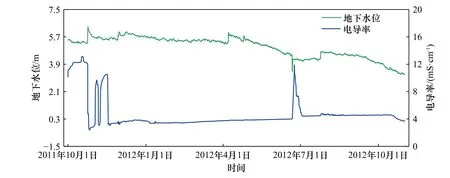
图7 监测井BH4 水位与电导率变化Fig.7 Groundwater level and electrical conductivity variation in BH4 monitoring well

3.1.2 电导率动态变化特征

根据研究区2011–2012 年各监测井采集的电导率动态数据，计算各监测井电导率的最大值、最小值、平均值、标准差以及标准离散率等空间变化统计特征，结果见表2。

表2 监测井电导率统计特征分析（单位：mS/cm）Table 2 Analysis on statistical characteristics of electrical conductivity in monitoring wells (unit:mS/cm)

标准离散率θ的计算公式为

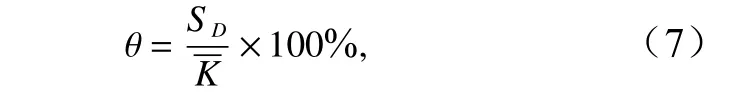
式中，SD为电导率的标准差；K为电导率的平均值。

温度为20℃时，天然水的电导率介于0.5～1.5 mS/cm。在滨海地区，电导率可以作为一项评判海水入侵的指标，电导率的值越小说明地下水受海水入侵程度越低[41–42]。由上表可以得出，监测井BH1、BH2 和BH3 的电导率值大致在天然水电导率的范围附近，没有出现电导率异常现象，因此这几口监测井的地下水基本未受海水入侵的影响；而BH4、BH5 及BH6 的电导率值远超出该范围，说明地下水在很大程度上受到海水入侵的影响。

从电导率的平均值来看，BH5 的值最高，水质相对较差，其主要原因可能与该处的地下水开采所导致的海水入侵有关，距离它较近的BH4 和BH6 的值也较高；BH3 的平均电导率最低，为1.20 mS/cm，说明此处的地下水质相对较好。监测井BH4 的标准离散率最高，为47.91%，说明该点地下水电导率相差较大；BH2 的标准离散率最低，为1.27%，说明该点的电导率的稳定性较高。

3.1.3 小波相干性分析

为了理解潮汐对地下水位和地下水电导率的影响，引入小波相干性识别潮汐与地下水位和电导率之间的统计关系。潮汐与地下水位和电导率之间的小波相干性分析结果如图8 所示（图中以监测井BH2和BH6 为例），谱之间的相位关系用箭头的方向表示。影响锥（白色虚线）表示小波谱的区域，在该区域由于基础数据的有限长度特性而产生的边缘效应不能被忽略。

图8 小波相干性分析Fig.8 Wavelet coherence analysis

（1）地下水位和潮汐之间的小波相干性分析

小波相干性分析结果表明，每口监测井的地下水位与潮汐数据之间存在不同的相干性。监测井BH2 和BH6，在整个时间序列中频谱值有相应变化（图8a 和图8b），这些频率代表地下水位对潮汐变化的响应。对于监测井BH2 和BH6，地下水位和潮汐在0.25 d 频率上的相干性很小，0.5 d 相干性较高，1 d的相干性相对较弱，但相关分布在不同时间是间歇性的。在0.5 d 周期内，与监测井BH6 同期地下水位和潮汐资料相比，监测井BH2 中的地下水位对潮汐的响应时间不同，相干性更弱，这可能与BH2 的位置及地质条件有关。小波相干性分析表明，海岸带含水层的地下水位受到海洋潮汐变化的影响。潮汐信号对地下水位的影响具有时空差异。靠近海岸的地区更容易受潮汐影响。同时，某些地区的潮汐效应一般与它们相对于海洋的位置和地质条件的综合效应相关[43]。

（2）地下水电导率和潮汐之间的小波相干性分析

图8c 和图8d 显示，将小波相干性分析应用于监测的地下水电导率数据和潮位时间序列时，未检测到连续的短期时间相关性。监测井BH2 在2012 年7 月1 日至2012 年10 月1 日时间段内电导率和潮汐之间存在16～32 d 的长周期相关性。监测井BH6 中电导率和潮汐之间存在短期的相关性，可以看出不同井位的电导率对潮汐变化的响应不同。潮汐对地下水电导率的影响要弱于对地下水位的影响，因为地下水位的波动是受应力变化的影响，而电导率的变化需要含水层储水量的体积变化。更重要的是，地质条件对控制潮汐对地下水位的影响至关重要。

3.2 模拟结果分析

3.2.1 水位模拟结果分析

WA-NARX 神经网络混合模型在NARX 神经网络模型的基础上，引入小波分析，对数据进行小波分解以减小预测误差，提高预测精度。在进行海岸带地下水位预测时，把降雨和潮汐作为输入参数，经WANARX 混合模型模拟得到地下水位预测结果，同水位的观测值进行对比，得到预测结果的散点图和时间序列图。图9 显示了BH1–BH6 这6 口监测井地下水位的预测结果。

图9a、图9c、图9e、图9g、图9i、图9k 为预测结果散点图，图9b、图9d、图9f、图9h、图9j、图9l 为预测结果时间序列图。通过预测结果散点图可得：训练数据和预测数据集中分布一条直线上，模型在水位变幅较大时预测效果有所降低。如图所示，监测井BH3 的散点出现小幅度的偏离。通过预测结果的时间序列图可得：训练和测试过程水位变化趋势与观测水位变化趋势一致。混合模型在训练和测试过程中均表现出较低的误差，在地下水位波动处误差相对较高，但模型总体上表现出良好的模拟效果。WANARX 神经网络混合模型在训练阶段和测试阶段的RMSE 和R2性能指标值见表3，从表3 可见，所有监测井在训练和测试阶段的R2均大于0.99，RMSE 均小于0.03，表明模型性能良好。

图9 WA-NARX 模型地下水位预测与观测对比Fig.9 Comparison of groundwater level prediction based on WA-NARX and observation

表3 地下水位预测时WA-NARX 模型的均方根误差（RMSE）和拟合度（R2）统计表Table 3 The WA-NARX model performance metrics of RMSE and R2 for groundwater level prediction

3.2.2 电导率模拟结果分析

BH1–BH6 6 口监测井电导率的预测结果散点图和时间序列图如图10 所示，从混合模型模拟结果可以看出：混合模型的训练数据和测试数据基本集中分布在一条直线上，电导率的变化趋势与观测电导率的变化趋势一致，在训练和测试阶段模型的误差都相对较低。因此WA-NARX 神经网络混合模型适用于地下水电导率的模拟预测。表4 中所有监测井在训练和测试阶段的R2均大于0.98，RMSE 均小于0.009，说明该模型在进行电导率的模拟预测时也表现出良好的性能。

表4 电导率预测时WA-NARX 模型的均方根误差（RMSE）和拟合度（R2）统计Table 4 The WA-NARX model performance metrics of RMSE and R2 for electrical conductivity prediction

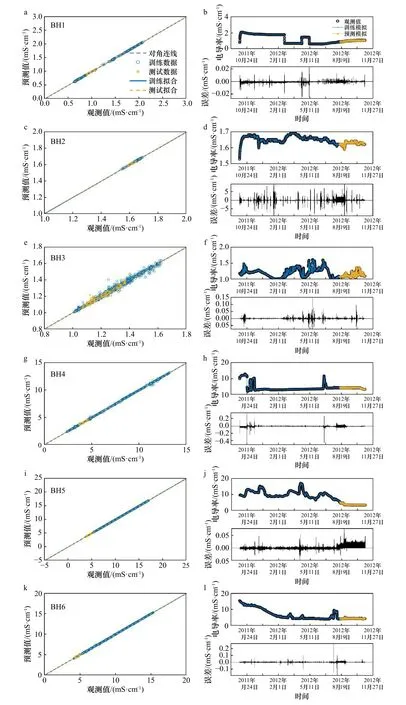
图10 WA-NARX 模型电导率预测的性能图Fig.10 Performance of WA-NARX model for electrical conductivity prediction

3.3 蒸发和排灌用电量对混合模型预测的影响

3.3.1 蒸发对水位预测的影响

在对比不同输入参数对地下水位预测结果的影响时，在模型训练完成后，关闭WA-NARX 网络的回路，输出反馈进行多步预测。以60 h 为时间步长进行多步预测。表5 为仅有降雨、潮汐参数的地下水位预测结果与新增蒸发参数后（降雨、潮汐和蒸发）的地下水位预测结果的对比。由预测误差可知，输入参数仅为降雨和潮汐时，模型的预测精度较高；当在此基础上新增蒸发作为输入参数时，模型预测结果发生了变化。与无新增参数的结果相比，监测井BH1、BH3 和BH6 的预测精度有所提高，其余监测井的预测精度有所降低。经过整体对比发现，只有降雨和潮汐作为模型的输入参数时，模型的预测效果略高于新增蒸发参数后的预测效果。说明在该地区进行地下水位预测时，降雨和潮汐对地下水位变化的影响更为显著。

图11 是新增蒸发参数后得到的预测水位与实测水位的散点图。图中实线是观测水位数据的连线，把降雨和潮汐作为WA-NARX 模型的输入参数，预测60 h 时间步长的地下水位时，模型的预测值基本分布在实测的水位线上，预测效果良好。新增蒸发参数后，监测井BH1、BH3 和BH6 的预测散点值更集中于实测水位线，表现出更好的预测效果，而其余观测井的预测效果相比之前有所下降，这与表5 的分析结果一致。

图11 新增蒸发参数的预测和实测地下水位散点图Fig.11 Scatter diagrams of predicted and observed groundwater level with newly added evaporation parameters

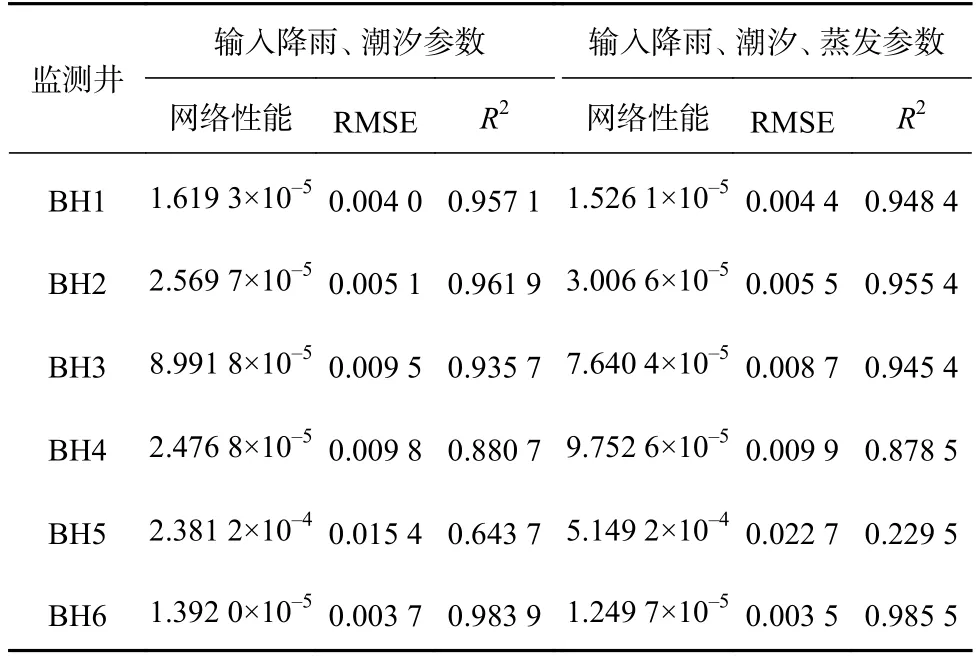
表5 新增蒸发参数的地下水位预测误差及网络性能统计表Table 5 The prediction error of groundwater level and network performance with newly added evaporation parameters

3.3.2 排灌用电量对水位预测的影响

农业排灌用电量与农业抽水灌溉有关，灌溉则与地下水位密切相关，所以把排灌用电量作为一组参数，研究其对地下水位预测的影响。表6 为新增排灌用电量参数与只有降雨和潮汐作为参数时地下水位预测结果的对比。由预测误差可知，只有降雨和潮汐作为输入参数时模型有较高的预测精度；当新增排灌用电量作为输入参数后，模型的预测精度同之前相差甚小。其中监测井BH5、BH6 的预测效果有细微的提高，其余监测井的预测效果有所降低。说明在研究区内农业排灌用电量数据可以作为预测地下水位的一项参数，在使用时要结合研究区监测井的实际情况，在农业抽水灌溉量较大处的影响会更显著。同时从电量时间序列可以看出，因统计关系，每个月的灌溉用电量基本为定值，而地下水位的预测周期是小时变化，所以，用电量的观测与地下水预测频率不完全一致，对模拟结果也有较大影响。如果用电量的统计频率与预测相符，模型的预测精度应有所提高。

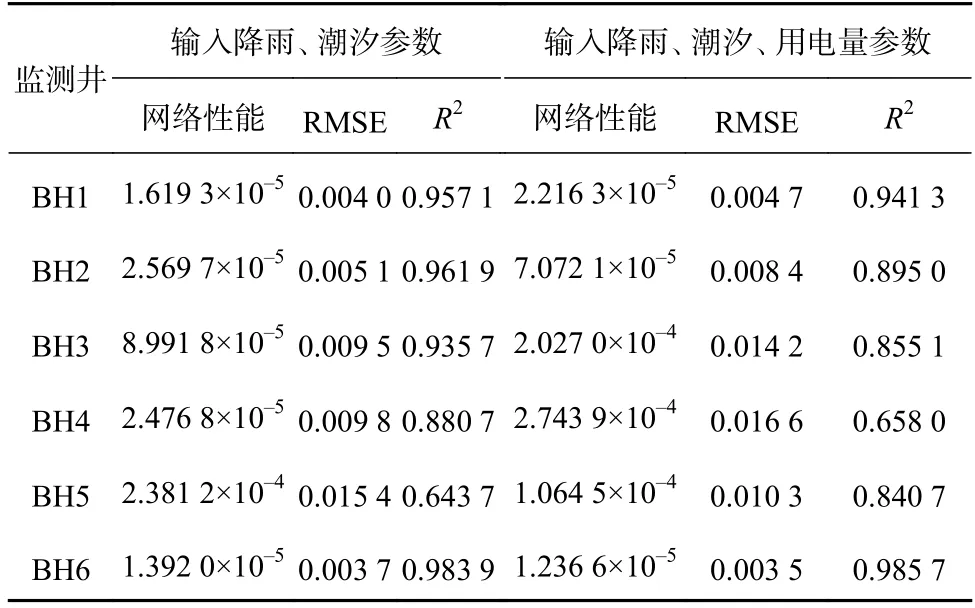
表6 新增用电量参数的地下水位预测误差及网络性能统计Table 6 The prediction error of groundwater level and network performance with newly added power consumption parameters

图12 是新增排灌用电量参数得到的预测水位与实测水位的散点图。从图中可以看出，每口井对新增排灌用电量参数后的预测效果响应并不尽相同。BH1 与BH6 的预测结果相对近似；而BH2、BH3 及BH4 的预测水位分布及表6 中RMSE 共同显示其预测值较只应用降水与潮汐时有所下降。对于BH5 来说，加入用电量后预测结果整体向上偏移，精度有一定提高。对比结果说明井位地理位置分布及其区域地质条件对用电量的响应有较大关联。

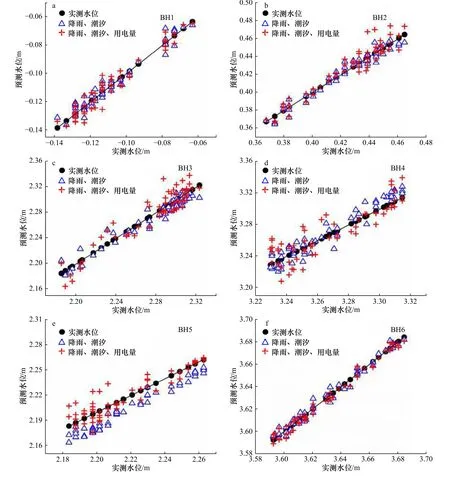
图12 新增用电量参数的预测和实测地下水位散点图Fig.12 Scatter diagrams of predicted and observed groundwater level with newly added power consumption parameters

3.3.3 蒸发对电导率预测的影响

图13 是新增蒸发参数后得到的预测电导率与观测电导率的曲线图，表7 为不同输入参数地下水电导率预测结果的对比统计表。由分析结果可知，在降雨、潮汐基础上增加蒸发数据作为输入参数时，无论在变化平缓区还是剧烈区，监测井中电导率的预测精度都有显著提高。特别对监测井BH5，未加入蒸发数据时预测值略有偏高，加入蒸发对该井有明显的校正作用。预测结果说明在该地区预测地下水电导率时，蒸发是重要影响因素。

图13 新增蒸发参数的预测和实测电导率曲线图Fig.13 Curve diagrams of predicted and observed electrical conductivity with newly added evaporation parameters

3.3.4 排灌用电量对电导率的影响

为了对比不同输入参数对地下水电导率预测结果的影响，关闭WA-NARX 网络的回路，输出反馈进行多步预测。把收集到的农业抽水排灌用电量数据作为一项参数，对比其对地下水电导率预测效果的影响。由表7 可知，只有降雨和潮汐作为输入参数时，模型有较好预测效果；新增农业排灌用电量参数，监测井BH1、BH2 和BH5 的预测效果有所提高，其余监测井的预测效果基本保持一致，总体上新增排灌用电量参数后混合模型的预测效果有所提升。

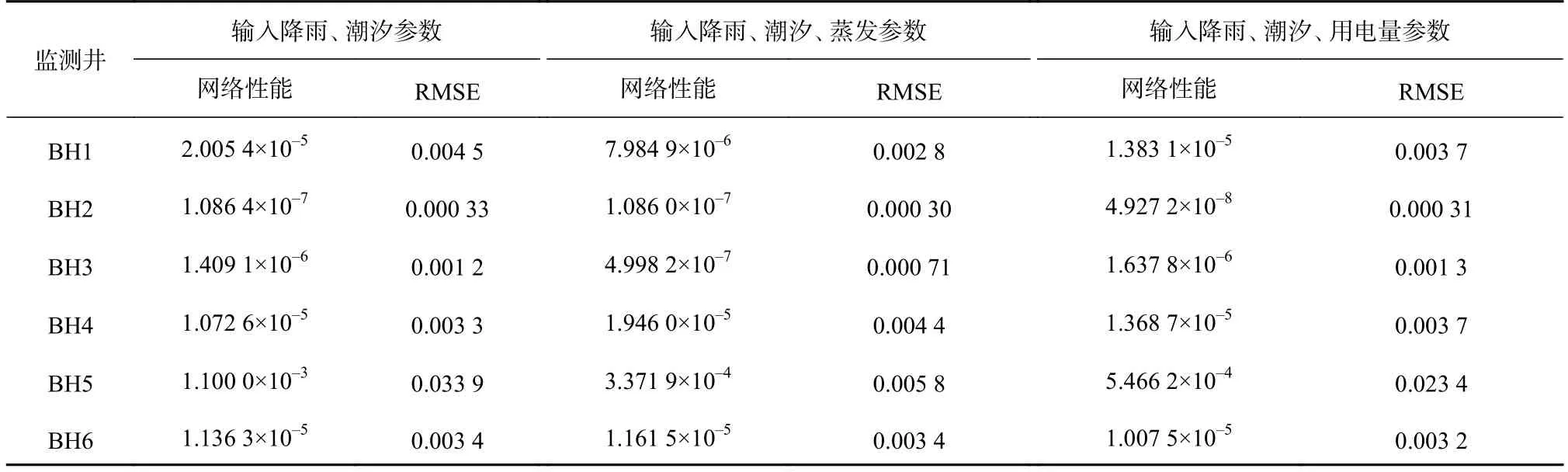
表7 不同输入参数电导率预测误差及网络性能评价统计Table 7 The prediction error of electrical conductivity and network performance with different input parameters

图14 是新增排灌用电量参数得到的预测电导率与观测电导率的曲线图。预测值的变化趋势和实测电导率的变化趋势基本吻合，表现出较好的预测效果；当新增农业排灌用电量参数时，监测井BH1、BH2 和BH5 的预测曲线与观测电导率曲线的变化趋势更加贴合，与表7 的分析结果一致。

图14 新增用电量参数的预测和实测电导率曲线图Fig.14 Curve diagrams of predicted and observed electrical conductivity with newly added power consumption parameters

4 结论与展望

莱州湾南岸是受海水入侵影响严重地区。通过对沿海典型剖面含水层地下水位和电导率的变化分析可知，该区海水入侵季节性变化趋势明显。主要表现在地下水电导率与水位存在一定的负相关关系，在降雨补给充足的情况下，地下水水位有较为明显的上升趋势，地下水电导率降低，海水入侵程度减弱。但由于受地下水开采的影响，水位和电导率均存在突变现象，水位降低打破原有的咸淡水平衡，使海水入侵加剧。同时，本文建立了基于小波分析的非线性自回归神经网络混合模型（WA-NARX），分别对地下水位和地下水中的电导率进行预测，通过增加模型的输入参数，对比分析不同输入参数对模型预测效果的影响。研究发现，地下水位和电导率的变化与降雨和潮汐的变化密切相关。当降雨和潮汐作为模型的输入参数预测地下水位与电导率时，模型预测效果良好。蒸发参数和农业排灌用电量对地下水位与电导率也有一定影响。模型预测依然具有较高精度，个别观测点精度有所提高。通过上述研究表明，WA-NARX 模型可以作为海水入侵预测的有效工具，不仅可以为水资源的高效利用提供参考，还可以掌握海岸带地下水盐度的变化，为海水入侵的监测预测预警、保护地下淡水资源及海岸带环境保护提供科学依据。