荷载不确定移动机器人视觉伺服系统鲁棒预测控制
邢科新,倪伟琦,何德峰
(浙江工业大学信息工程学院,浙江杭州 310023)
1 引言
随着移动机器人应用需求的日益复杂多样,传统的控制手段不再满足应用需求,而视觉伺服[1-3]被广泛认为是使机器人更加灵活和快速的有效解决方案,因此在移动机器人领域得到了广泛的应用[4-6].通常情况下移动机器人视觉伺服将误差信号定义在图像特征空间,通过选择合适的视觉特征和视觉控制来达到满意的控制效果[5].然而移动机器人是一个典型的具有非完整性约束的欠驱动系统,这使得视觉伺服技术在实际应用中具有挑战性.
移动机器人视觉伺服控制需要兼顾视觉传感器和机器人的特性,因此视觉伺服过程中会受视觉传感器的视场约束以及移动机器人执行机构的物理约束,如果违反这些约束,则会导致视觉伺服任务不能有效地执行,甚至导致失败[7-9].为解决约束问题,一些学者利用分层的思想来处理移动机器人视觉伺服问题,如文[10]针对移动机器人单目视觉伺服提出了一种自适应视觉跟踪控制器,首先基于一阶滤波器设计了虚拟速度控制器,然后根据有限时间理论设计加速度控制器,从而在有限时间内跟踪虚拟速度输入,在视觉伺服过程中保证了速度和加速度饱和约束;文[11]提出了一种综合轨迹规划和跟踪控制的视觉伺服方法,将轨迹规划阶段纳入到视觉伺服中,在规划过程中处理了视场和速度约束.
近年来,模型预测控制(model predictive control,MPC)由于具有显式处理约束和系统不确定性的能力受到了众多学者的青睐[12-13],并被广泛应用在移动机器人上,如文[14]提出了一种基于图像的视觉伺服控制策略,利用MPC来稳定一个有物理约束的移动机器人;文[15]提出了一个基于机械臂的图像视觉伺服方案,通过采用MPC策略最小化基于图像误差的代价函数来计算控制信号,并能显式地考虑可见性约束和转矩约束;文[16]考虑六自由度机器人视觉伺服系统的物理限制和可见性约束,提出了一种基于鲁棒MPC(robust MPC,RMPC)方法和在线图像的视觉伺服控制器.与基本视觉伺服控制器相比,MPC可将视觉伺服系统控制在期望范围内,因此大大增加了移动机器人视觉伺服任务的成功率.
在实际应用中,移动机器人的动态系统相对较快,实时性要求较高,而MPC在每个采样时刻要在线实时求解一个有约束的优化问题[17],在优化过程中往往需要大量的计算,限制了MPC的应用范围,导致并不能满足移动机器人实时性的要求.因此克服MPC在线优化计算量大的问题显得尤为重要.对此,文[18]提出了一种基于事件触发的RMPC控制器设计方法,在优化过程中当满足事件触发条件才进行优化,通过减少在线优化次数,一定程度上减少了系统的计算负担;文[19]针对受限移动机器人视觉伺服系统,提出一种移动机器人视觉伺服镇定准最小最大MPC策略,所设计的控制器只需求解线性矩阵不等式表示的凸优化问题,降低了MPC在线计算量,减少了计算耗时,并保证了系统的渐近稳定性.虽然上述文献一定程度上减少了在线计算量,但在实际情况中计算耗时仍然较长,设计的控制器并不能很好地满足实时性控制要求.
为满足移动机器人实时性控制要求,降低在线优化的计算量,针对受限移动机器人视觉伺服系统,本文设计了一种鲁棒视觉伺服控制器.首先对移动机器人视觉伺服系统进行分层设计,将视觉伺服系统分为两个子系统,然后对视觉伺服误差子系统设计速度规划预测控制器,获得机器人的期望速度,在进行速度规划设计时结合多Lyapunov函数min-max预测控制策略[20]和准最小最大模型预测控制策略,提出了一种基于半正定规划的速度规划高效MPC算法,通过将算法分为离线算法和在线调度两部分,大大减轻了在线计算负担,降低了视觉伺服预测控制器的计算耗时,同时保证了闭环视觉伺服系统的渐近稳定性.为了使移动机器人的实际速度渐近于期望速度,采用鲁棒预测控制策略对视觉伺服速度子系统进行期望速度跟踪预测控制,鲁棒预测控制可以更快地达到稳定状态.最后通过仿真验证所提出的控制器能够驱动移动机器人达到期望位姿,并且系统的闭环响应更为快速和稳定,满足移动机器人快速响应实时性控制要求.
2 问题描述
考虑如图1所示的移动机器人视觉伺服系统,其中,世界坐标系O-XY Z,机器人坐标系Or-XrYrZr,相机坐标系Oc-XcYcZc.假设Oc-XcYcZc方向与Or-XrYrZr方向一致,且Y轴重合,原点相距l.令原点O为机器人在O-XY Z的目标位置,选取目标位置上方的P点为特征点.

图1 移动机器人视觉伺服系统Fig.1 Visual servo system of mobile robot
考虑图1中的移动机器人,假设其存在纯滚动无滑动运动,则建立移动机器人运动-驱动模型[21]

其中:(x,y)为机器人质心在O-XY Z的坐标,θ为机器人朝向角,v和ω分别为线速度和角速度,m为机器人质量和载荷量总合,I为机器人转动惯量,τ1和τ2分别为机器人线转矩和角转矩.令q=[x y θ]T和ν=[v ω]T分别表示机器人的位姿和速度向量,则系统(1)可描述为如下分层系统:
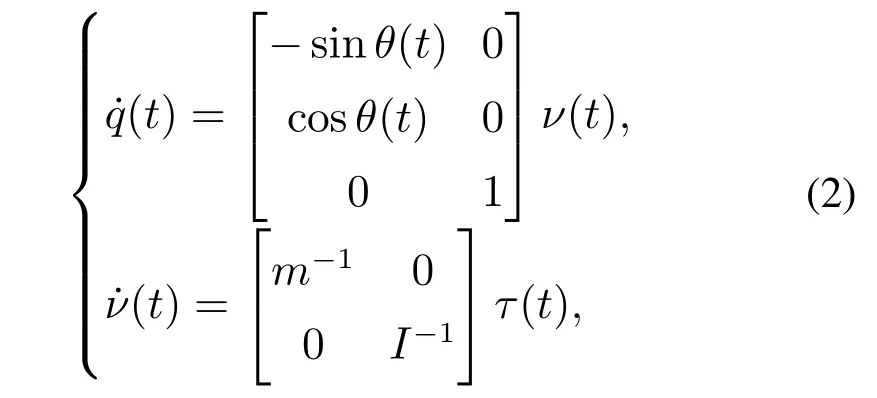
其中:控制输入τ=[τ1τ2]T,q子系统为机器人运动学模型,ν子系统为机器人动力学模型.在实际中,机器人载荷量通常是变化的,即m是一个有界不确定参数,满足mmin≤m≤mmax,其中mmin和mmax分别为机器人空载的重量(即自身质量)和满载的重量.
为建立移动机器人视觉伺服系统模型,引入如下坐标变换:

其中:(xp,yp)为点P在图像坐标系的坐标,(xpd,ypd)为目标点在图像坐标系的坐标,f为相机焦距,本文假定f不变.由相机模型可知,xp=(u-u0)/ku,yp=(υ-υ0)/kυ,其中(u,υ)是对应的像素坐标,(u0,v0)是像素平面中心,ku,kv是图像坐标中单位距离的像素数.再定义视觉伺服误差向量e=[e1e2e3]T

其中:角度误差θe=θ-θd,θd为目标朝向角度,θe可以根据运动估计算法[22]获得.则结合模型(1)及重量变化,采用文[21]推导方法,可得不确定移动机器人视觉伺服系统模型为

其中:高度系数α=1/Zc,Zc为特征点P的高度.本文假设特征点高度不变,即α是一个常系数.对应系统(2),同理得移动机器人分层视觉伺服系统模型
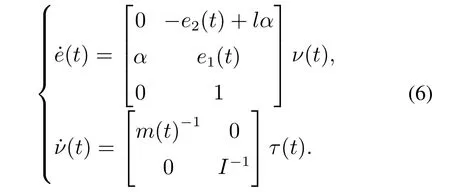
进一步,为保证有效执行视觉伺服任务,机器人移动范围、速度和转矩需要满足物理约束和视觉可见性约束条件
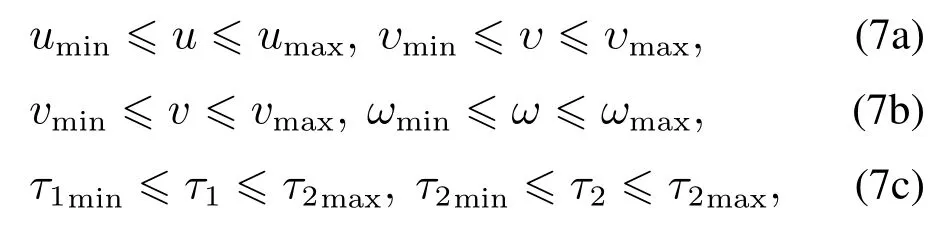
其中:下标“min”表示对应变量的取值下界,下标“max”表示对应变量的取值上界.
本文目标是在满足系统约束(7)条件下,将载荷量不确定的非完整移动机器人(1)驱动到目标特征点,并得到期望位姿,即视觉伺服误差e和控制量τ都趋于零.本文将对系统分层设计,并采用MPC方法设计非完整移动机器人系统(1)的鲁棒视觉伺服控制器.
3 鲁棒视觉伺服MPC控制器设计
考虑移动机器人视觉伺服系统(6)的分层结构,注意到不确定参数在ν子系统,因此为降低视觉伺服MPC的在线计算量,本节先对视觉伺服误差e子系统设计速度规划预测控制,获得机器人的期望速度,再对ν子系统进行期望速度跟踪预测控制,使得实际速度与期望速度ϑ(k)的误差趋向于0,从而控制移动机器人到达期望位姿.本文提出的移动机器人分层视觉伺服控制系统结构如图2所示.

图2 移动机器人分层视觉伺服系统控制框图Fig.2 Control block diagram of hierarchical visual servo system for mobile robot
3.1 速度规划预测控制
考虑移动机器人视觉伺服误差e子系统,令采样时间为T1>0,采用欧拉法离散连续时间系统(1),得到对应离散时间视觉伺服误差模型为

由于视觉伺服系统要满足约束(7),因此,B(p)可以分解成多个已知顶点的凸多面体Ω组合[23],即

进一步,由于视觉伺服误差模型(8)的非线性和多变量特性,传统视觉伺服MPC需要在线优化一个非凸的非线性规划问题[15],在线计算量大,难以满足移动机器人快速响应实时性控制要求.下面给出一种基于半正定规划的速度规划高效MPC算法,该算法分为离线计算和在线调度两部分.
1) 离线计算.
考虑离散时间视觉伺服误差子系统(8),定义无穷预测时域目标函数

其中:Q ∈R3×3和R ∈R2×2分别为误差状态和控制加权矩阵,e(i|k)和ν(i|k)分别为在当前k时刻对k+i时刻的预测量.考虑当前k时刻的误差状态e(k),则基于min-max策略,定义视觉伺服速度优化控制问题

其中:增益矩阵F=Y G−1,G ∈R3×3为松弛正定矩阵,Y ∈R2×3为待求矩阵.
考虑离散时间视觉伺服误差子系统(8),根据文献[24-25]推导可得,优化问题(11)等价为在该系统凸多面体每个顶点的优化,即


其中ρ>0为闭环视觉伺服误差子系统的误差衰减率.
为进一步减小优化问题(13)-(14)的在线计算量,离线迭代构造一系列嵌套的椭圆不变集序列.
算法1
a) 初始化衰减率ρ=1;
b) 求解优化问题(13)-(14),若该问题有可行解,则转入c)步骤;若没有可行解,则此时的ρ为最小衰减率,并存储ρ和相对应的优化函数上界γ;
c)ρ=ρ-0.01,重复b)步骤.
算法2
a) 给定初始状态量e1和循环次数N,令i=1;
b) 使用算法1计算状态量ei所对应的最小衰减率ρi;

通过算法1寻求优化问题(13)-(14)的最小衰减率ρi,最小衰减率可以保证闭环系统的稳定性.通过算法2得到每个状态ei所对应的优化值函数上界γ及其对应的Qi,j、最小衰减率ρi,对于凸多面体各个顶点,可以得到对应的椭圆不变集.通过确定最大矩阵Qi,m可以得到不变的椭球体[24].注意,矩阵Qi,m可以是矩阵Qi,j的凸组合,可由如下优化得到

其中L为椭圆不变集数量.注意,优化(17)得到的椭圆不变集是最小不变集εi.进一步存储每个误差状态ei所对应的上界γ及Qi,m,以备在线计算时调用.
2) 在线调度.
在线算法利用得到的离线嵌套椭圆不变集序列将误差状态收缩到一个更小的椭圆不变集中.假定当前时刻视觉伺服误差子系统(8)的状态e(0|k)∈εi,且e(0|k)/∈εi+1,需要求得一个合适的控制律驱动系统下一时刻的误差状态收缩到椭圆不变集εi+1.考虑无穷预测时域目标函数(10),将其分成两部分,即


考虑目标函数(18),极小化其在最坏情况下的上界λ,在线算法只需计算当前时刻的规划速度ν(k),相应在线算法的优化问题定义为
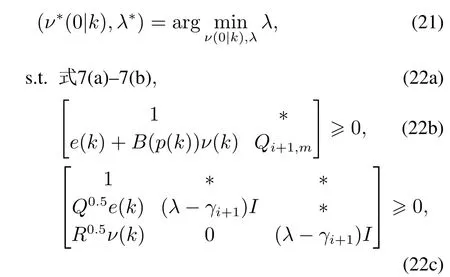
其中:(ν∗(0|k),λ∗)表示当前时刻的最优解,式(22a)表示规划速度约束和视觉可见性约束,约束条件(22b)构建了椭圆不变集εi+1,式(22c)表示最坏情况下目标函数(k)满足式(20),注意,式(22c)可对式(20)应用Schur补引理[23]得到.
在线求解优化问题(21)-(22),得到当前时刻的规划速度ν∗(k)=ν∗(0|k)和对应闭环视觉伺服误差系统

注1通过对视觉伺服误差子系统设计速度规划预测控制算法,可以获得机器人期望速度νc=[vcωc]T.该算法通过将目标函数分为当前时刻和未来时刻的目标函数,先离线构造椭圆不变集,将大部分MPC计算量移至离线算法,再在线调用离线计算存储的γi+1及Qi+1,m,只需在线计算当前控制律,大大压缩了MPC优化问题的决策变量的个数,因此在线求解时计算量大幅降低.注意,优化问题(21)-(22)是一个半正定规划问题,本文将基于半正定规划的速度规划MPC算法简称为高效MPC策略.
定理1考虑移动机器人视觉伺服误差子系统(8),如果优化问题(21)-(22)在初始时刻是可行的,即初始状态x(0)满足≤1时,那么该优化问题得到的速度规划控制律可以保证闭环视觉伺服误差子系统的渐近稳定性.
证由文献[24-26]推导可知,当优化问题(21)~(22)是初始时刻可行时,在后续每个时刻都存在可行解,即满足优化的递推可行性,从而优化问题在所有时刻都存在最优解.
考虑移动机器人闭环视觉伺服误差子系统(23).注意到离线算法在状态量ei下求解优化问题最小值的附加约束可等价写成,可得左侧不等式保证椭圆不变体的单调递减性,右侧不等式确保算法的可行性.进一步,控制律可驱动误差系统状态到最小椭圆不变体,并使之收敛到零,则当初始状态x(0)满足时,即初始状态e(0)∈ε1,其中ε1为椭圆不变集,优化问题(21)-(22)得到的状态反馈控制律可以保证视觉伺服误差系统的渐近稳定性. 证毕.
3.2 速度跟踪预测控制
考虑载荷不确定移动机器人视觉伺服驱动子系统,取驱动子系统采样周期为T2,建立对应离散时间视觉伺服驱动子系统如下:

令νc为移动机器人速度规划预测控制获得的期望速度ν∗,定义速度误差变量ϑ=νc-ν.本小节目的是计算转矩τ(k),使得实际速度与期望速度的误差ϑ(k)趋向于0.由于载荷存在不确定性,本文采用极小极大鲁棒MPC设计视觉伺服驱动控制器.
考虑离散时间视觉伺服驱动子系统(24),定义无穷预测时域目标函数

其中Qv ∈R2×2和Ru ∈R2×2分别为速度误差状态和控制输入加权矩阵,ϑ(i|k)和τ(i|k)分别为在当前时刻k对k+i时刻的预测量.考虑当前时刻k的速度误差状态ϑ(k),则定义视觉伺服速度误差优化控制问题
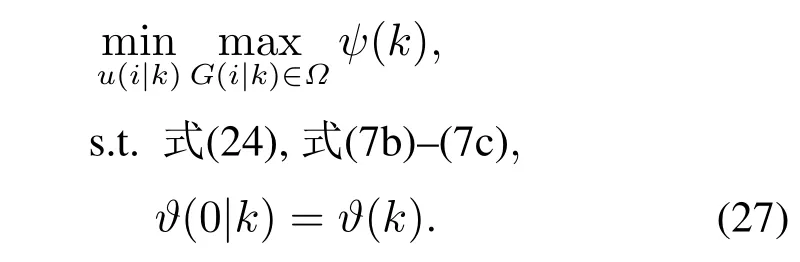
考虑到min-max优化问题的计算量大问题,构造状态反馈控制律τ(i|k)=Fϑ(i|k),其中F为控制器增益矩阵.则由文献[24-25]推导可得,优化问题(27)等价为在系统凸多面体(25)每个顶点的优化问题,即在每一个采样时刻,对目标函数ψ(k)在最坏情况下的上界γ求最小化

其中:不等式(29a)构建了椭圆不变集,不等式(29b)保证了闭环视觉伺服驱动子系统的稳定性[23],不等式(29c)为控制输入约束.
通过在线求解优化问题(28)-(29),可得最优解Y ∗和Q∗,则控制器增益矩阵F=Y ∗Q∗−1,对应最优转矩控制律τ(k)=Y ∗Q∗−1ϑ(k)和闭环视觉伺服驱动子系统

等价于闭环速度跟踪误差偏差系统

为建立移动机器人闭环视觉伺服驱动子系统(30)的渐近收敛性,考虑其闭环速度跟踪误差偏差系统(31)的内部稳定性结果.
定理2考虑移动机器人视觉伺服驱动系统(24),如果优化问题(28)-(29)在初始时刻是可行的,则它们在所有时刻都存在最优解,且该优化问题得到的状态反馈转矩控制律可以保证闭环速度跟踪误差偏差系统(31)的渐近稳定性.
证由文献[24-26]推导可知,当优化问题(28)-(29)在初始k时刻是可行的,那么在t>k的每个时刻都是可行的,因此优化问题在所有时刻都存在最优解.
考虑移动机器人闭环速度跟踪误差偏差系统(31)的内部偏差状态ϑ,选取子系统的一个候选Lyapunov函数
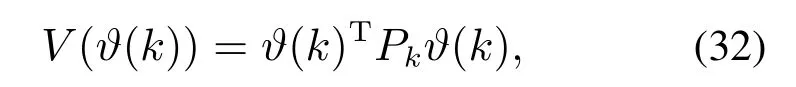
其中Pk为在k时刻Q∗的逆矩阵.则由文献[21]可知,对于任何载荷不确定性m(k),矩阵Pk在k+1时刻依然是可行解,即

进一步,由最优性原理可得

又注意到函数V(ϑ)是一个正定函数,存在上下界,故V(ϑ)是闭环系统(31)的一个Lyapunov函数,从而对于任何载荷不确定性m(k),移动机器人闭环速度跟踪误差偏差系统(31)是渐近稳定的. 证毕.
4 仿真结果与分析
为验证本文算法的有效性,本节进行了仿真实验.在仿真实验中使用硬件为处理器Intel(R)Core(TM)i5-4200H CPU@2.80GHz和内存为8.0GB的计算机,优化问题求解采用MATLAB 2019a软件中LMI工具箱求解.移动机器人的质量和载荷量总量为4~8 kg,即4 kg ≤m≤8 kg,移动机器人的转动惯量I=2.5 kg·m2.相机放置在距离机器人质心l=0.1 m处,其中相机的焦距f=6 mm,图像分辨率为640×480 pixels,目标点所在高度Zc=0.4 m.
在仿真实验中取采样时间T1=0.2 s和T2=0.1 s,加权矩阵Q={2,0.1,2},Qv={120,120},R={0.01,0.01},Ru={0.1,0.1}.在仿真实验中采用4个静态点作为特征点,假定移动机器人在世界坐标系的初始位姿为(1.6,-5,0),期望位姿为(0,0,0),可以求得偏差初始值为(-4,-12.5,0).进一步,考虑移动机器人视觉可见性约束和系统约束为

根据视觉可见性约束可得到移动机器人相应的误差量范围为e1∈[-15.8 8.7],e2∈[-22 22.5].
在视觉伺服速度规划部分将本文算法与传统准极小极大MPC算法[19]和常规MPC算法[22]在相同的仿真环境下和参数设定下进行对比,在速度跟踪部分应用本文算法对3种算法下得到的期望速度进行跟踪控制.图3和图4分别给出了移动机器人视觉伺服误差子系统在3种控制算法下的误差状态量和期望速度规划的仿真图,其中,实线对应本文算法的仿真结果,虚线对应传统准极小极大MPC算法的仿真结果,点线对应常规MPC算法的仿真结果;图5给出了本文算法下图像特征点在相机像素坐标系中的轨迹图;图6给出了移动机器人在X-Y平面的运动轨迹图,其中箭头表示移动机器人的朝向.图7分别给出了移动机器人视觉伺服驱动子系统在不同速度规划MPC策略下的速度跟踪控制效果和转矩的仿真图,其中,图7上两子图实线为误差子系统规划的期望速度,虚线为驱动子系统速度跟踪控制实际结果;图7最下子图实线为驱动子系统的角转矩输入曲线,虚线为驱动子系统的线转矩输入曲线.

图3 误差状态Fig.3 Error state
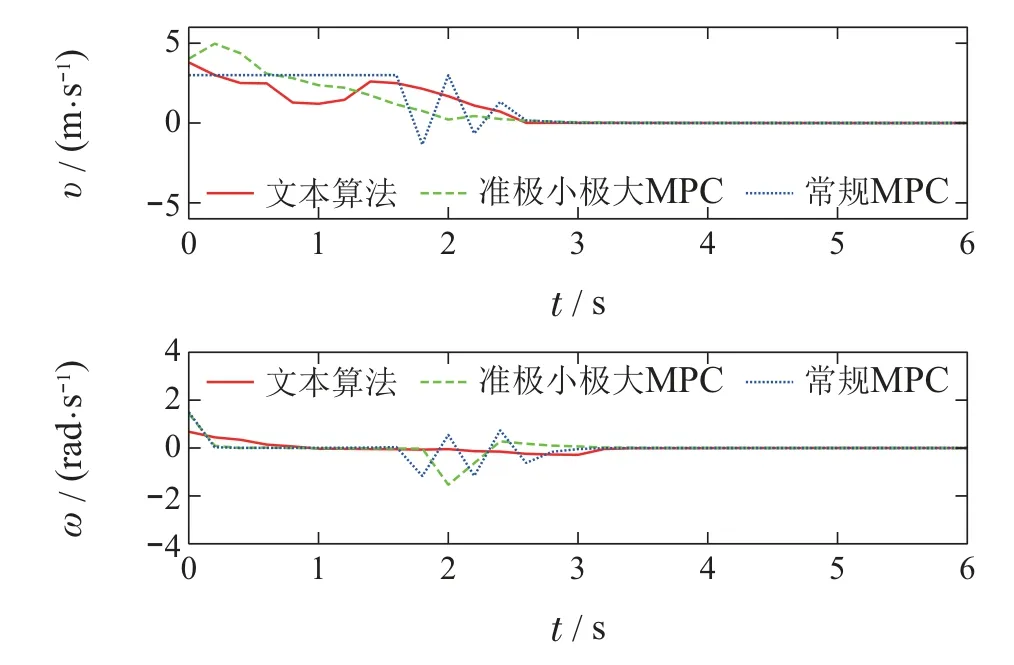
图4 规划速度Fig.4 Desired velocity

图5 图像特征点轨迹图Fig.5 Trajectory diagram of image feature points

图6 移动机器人运动轨迹图Fig.6 Trajectory of the mobile robot


图7 期望速度、实际速度和转矩Fig.7 Desired speed,actual speed and torque
分析图3-4可知,本文控制算法、传统准极小极大MPC算法和常规MPC都能规划出移动机器人到达目标位置的速度轨迹,同时满足视觉伺服系统的约束.3种算法驱动误差状态到达稳态的时间(即过渡时间)基本相同,但是本文MPC算法规划的期望速度较传统准极小极大MPC算法和常规MPC规划的期望速度更加平缓,这有利于速度跟踪控制器的控制,从而使得移动机器人可以更加平稳运行.由图5和图6可知,在本文控制算法下,移动机器人最终到达期望位姿.并且由图5可知特征点一直在相机视野范围内,满足了视觉伺服系统的视觉可见性约束.
进一步分析图7可知,对于由3种MPC算法规划的期望速度,本文设计的鲁棒MPC都能实现快速跟踪,即移动机器人在1.4 s就达到了规划的期望速度.同时,计算得到的线转矩和角转矩变化平稳,有利于机器人驱动电机的运行.此外,线转矩和角转矩都满足伺服系统的约束条件.这些表明,对于机器人载荷不确定,本文设计的速度跟踪鲁棒预测控制策略具有良好的鲁棒渐近稳定性能.
最后考虑MPC优化问题在单步优化的计算耗时性能.由表1可知:1)在3种算法中,当速度规划采用本文MPC算法时,所需的平均单步计算时间最小.相比于在相同仿真环境下的传统准极小极大MPC算法和常规MPC算法的单步计算时间,本文的MPC策略大大缩短了计算时间.2)本文算法速度规划和速度跟踪的平均单步计算时间均小于采样时间,可以保证移动机器人运动的实时性要求,而传统准极小极大MPC算法和常规MPC的平均单步计算时间超出了采样时间,并不能满足实时性的要求.3)本文算法总的平均单步时间为0.161 s,而传统准极小极大MPC算法和常规MPC的算法总的平均单步计算时间分别为0.262 s和0.312 s.因此,可以看出,本文算法可以大大减少计算时间,提高计算效率,快速镇定移动机器人到目标位置,满足实时性的要求.

表1 单步计算时间Table 1 Calculation time for each step
5 结论
针对受限荷载不确定移动机器人视觉伺服系统,本文设计了一种分层鲁棒视觉伺服预测控制策略.在视觉伺服速度规划部分通过将大部分计算量转移到离线算法计算,大大降低了在线计算量.在视觉伺服速度跟踪部分采用鲁棒预测控制实现了对期望速度的快速跟踪.所设计控制器有效降低了鲁棒视觉伺服预测控制器的在线计算量,从而更好地满足移动机器人快速响应实时性的要求.仿真对比实验结果验证了本文控制策略的有效性和优越性.后续将进一步开展所提控制策略的实验验证研究.

