车辆提前掉头几何参数设置及阈值流量研究

张小龙， 赵 界， 李 冰， 杨鸿宇

(1.通号智慧城市研究设计院有限公司， 北京 100071； 2.昆明理工大学 交通工程学院， 昆明 650500)

城市道路车辆掉头的方式通常有交叉口掉头和路段提前掉头，前者指车辆在交叉口区域内或进口道停车线前完成掉头；后者指车辆在交叉口之间的路段上完成掉头，车流绕行距离相对较小且一般情况下不受信号控制的影响。目前，国内外对城市道路车辆提前掉头的研究多集中于掉头口几何设置方式、对交叉口运行安全以及通行效率影响等方面。刘书鹏等[1]通过实例调查并结合交通仿真，总结路段掉头交通组织的设置方法和优缺点，分析了路段提前掉头在城市道路中实施的可行性，并基于城市道路条件、路段设计和交通管理等方面提出了相应的设置建议。Shao等[2]设计出一种“丁”字掉头车道，并结合VISSIM仿真进行验证，结果表明与传统掉头车道相比，该种设计可节约掉头车辆29.15%的行程时间和66.70%的延误以及最多100%的停车次数。Mazaheri等[3]利用交通仿真模拟分析出信号交叉口路段车均延误最小的掉头位置。成卫等[4]基于掉头车流交通运行特性，通过计算掉头车辆饱和流率，得出掉头车流对下游交叉口通行能力的影响。邵海鹏等[5]基于排队论和车辆换道模型，并结合交通仿真，提出了3种典型掉头交通设计模式下路段开口大小及位置计算模型。林培群等[6]基于可插车间隙理论和稳态延误理论，建立了“直接左转”与“远引掉头”的车均延误计算模型，并得出2种方式各自的适用条件。孙峰等[7]基于车辆通行效率，通过分析掉头车道车均延误的及计算通行能力，提出了路段掉头开口位置最优计算模型。Mohapatra等[8]通过研究路段掉头开口区域，将掉头车流与对向直行车流之间的冲突区域分为3个部分：严重冲突区域、安全区域和未受影响区域，并分别计算异质交通流的冲突量，提出了相应的计算模型。

综上分析，对于设置城市路段车辆提前掉头的左转及掉头车流量阈值条件等问题，国内外研究相对较少。为此，本文在国内外现行城市道路掉头设计方案及开口位置选址模型等研究的基础上，根据道路交通实际状况，应用科学定量的方法对交叉口路段车辆提前掉头交通设置进行分析，提出车辆提前掉头关键几何设置参数计算方法及阈值流量条件。

1 关键几何参数理论计算

以传统四相位信号控制交叉口为研究对象，进行相关理论参数计算，如图1所示。掉头口设置在左转及掉头共用车道中段，掉头处不设信号灯，掉头车辆在开口处汇入对向车道时，在相位a和d会受到对向直行冲突车流的影响。分析可知，判断路段掉头车流设置是否合理以及运行效率优劣的关键几何参数有：掉头开口位置、掉头车流在开口处的排队长度以及调头开口大小等。

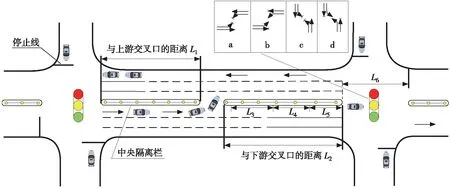
图1 车辆提前掉头运行及信号相位示意

1.1 提前掉头开口位置设置

掉头开口位置如果与上游交叉口距离L1过短，则排队掉头车辆会影响同向左转车辆驶出交叉口；如果L1距离上游交叉口过长，则将增加掉头车辆绕行距离，失去提前掉头开口设置的必要性，并且当开口设置在下游交叉口功能区域内时，车辆运行环境更复杂，不同车流间影响较大，这将增加交通事故发生率。因此，确定掉头开口位置对整个交叉口车流运行非常关键。

1) 与上游交叉口的距离L1

车辆在城市路段开口处的掉头过程可看作一个排队系统[9]，当不受信号控制的掉头车辆在进入对向车道时，会受到直行车流的影响。车辆在刚驶离上游交叉口时，由于不受道路信号控制且行驶速度相对较快，因此掉头开口与上游交叉口的距离应该大于掉头车辆在开口处的最大排队长度和必要的安全停车视距。

掉头车流到达开口处时，车流量不大且不受信号控制时，交通流处于自行调整状态，可认为掉头车流到达服从泊松分布；而对向车流由于靠近开口处，会适当降低车速，其饱和度较大，此时车辆间相互影响的作用也随之增加，车辆到达不再是随机的，Erlang分布则可较好地描述介于随机和恒定到达状态之间的交通状况，因此可由Erlang分布拟合冲突车流到达开口处的车头时距。故可用排队模型M/EK/1来描述掉头车流在开口处的排队掉头过程，该排队模型为[10]：

p0(0)=1pn,s(0)=0n≥1 1≤s.≤k.

(1)

式中：β为排队系统中顾客的到达率；u为服务率(消散率)；pn,s(t)为在时刻t系统里有n个顾客，其中一个顾客在系统的第s相位里接受服务的概率。可把车辆平均到达率等同于排队系统中顾客到达率即β，把路段开口处通行能力看作是系统服务率即u，因此，若求得掉头车流小时交通量β′和掉头口处车辆掉头通行能力u′,即可求出掉头车流平均排队长度。

基于可插车间隙理论，当掉头车辆面临对向车流冲突间隙时(tf)，驾驶员会与其掉头可插车临界间隙时间(tc)相比较，当tf≥tc时才进行掉头，否则在掉头开口处排队等待，tc通常取5.5 s～6 s[9]，当tf满足1辆车的掉头间隙时，则可有1辆车掉头，当tf满足n辆车时，则有n辆车可进行掉头，可得ntc≤tf≤(n+1)tc。设pn为对向冲突车流通过掉头口时的车头间距可插入n辆车的概率，则有：

(2)

式中：P(T)为Erlang分布车头时距为T的概率；ω=K-1，K为Erlang分布阶数，取K=2；λ1为对向冲突车流到达率。(λ1-1)Pn表示在单位时间内存在的(λ1-1)个车头间隔中，通过n辆车的间隔数。因此，掉头口服务率u为：

(3)

最后根据M/EK/1排队模型可得掉头开口处平均排队车辆数Lq为：

(4)

掉头车辆排队长度为：

(5)

式中：lt为车辆停车平均车头间距，取7.5 m。

一般城市道路停车视距LT可由以下公式表示：

(6)

式中：ve为车辆驶出交叉口的速度，km/h；tr为驾驶员的感知反应时间，取1.5 s；ρ为车辆与路面间摩擦系数，取0.6；i为城市道路纵向坡度；l0为停车时两车间的安全距离，取3 m～5 m。

掉头开口与上游交叉口距离L1应至少大于掉头车辆最大排队长度与安全停车视距之和：

L1>(LP+LT)=

(7)

2) 与下游交叉口的距离L2

如图1所示，下游功能区长度由驾驶员在感知-反应时间内所行驶距离L3、车辆开始减速到完全停止所行驶的距离L4及左转车辆最大排队长度L5组成。因此，掉头口与下游交叉口停止线的距离L2应至少大于其功能区长度：

(8)

式中：vi为车辆接近交叉口的速度，m/s；a为车辆的平均减速度，取2 m/s2；q为路段左转车流高峰小时交通量，pcu/s；r为红灯时间，s。

1.2 掉头开口长度设置计算

基于车辆通行安全，中央隔离栏的掉头开口长度Ld一般由3部分组成[11]，如图2所示：车辆运行轨迹宽度Rt、车辆掉头起始位置区间长度h和车辆横向安全距离dc：

Ld=Rt+2dc+h

(9)

式中：h和dc通常取2.6 m和0.443 m[11]。Rt等于车辆在最小转弯半径下车头最外廓轨迹半径(R1)减去车辆后轮内沿半径(R2)：

Rt=R1-R2

(10)

(11)

式中：d1为车轮轴距；d2为车辆主销到外轮轮廓中心线距离；d3为掉头车辆的前悬距离，单位均为m；θ为外车轮转角。

图2 掉头车辆阻挡左转车辆

2 掉头车流运行效率研究

不计交叉口非机动车和行人干扰，设置路段掉头开口后左转与掉头共用车道的损失时间包括掉头车辆在路段开口处的排队延误和掉头车辆阻挡左转车辆带来的延误。

2.1 提前掉头车流排队延误

掉头开口处的排队延误(Dp)可分为掉头车辆排队等待延误(Dw)和进入对向车道后与直行车流的冲突延误(Dc)，即Dp=Dw+Dc。

由上述分析可知，车辆的掉头过程可看作M/EK/1排队模型，即等待时间：

(12)

式中：Lqi为掉头口处的排队车辆数，pcu；qi为掉头车流到达掉头口的流量，pcu/h。

对于掉头车辆的冲突延误，根据Sil等[12]的研究，当对向冲突车流量为1 000 pcu/h～2 000 pcu/h时，掉头冲突时间可取3.9 s～4.2 s。

2.2 掉头车辆阻挡左转车辆的延误

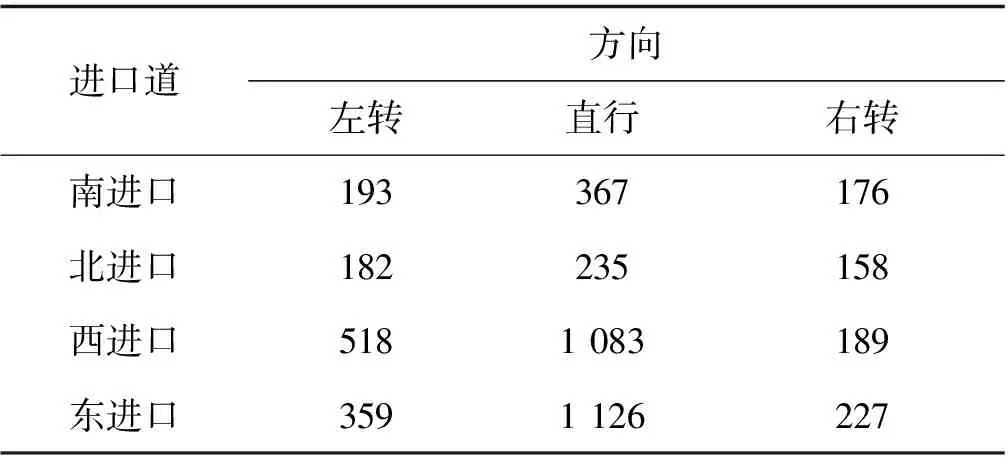
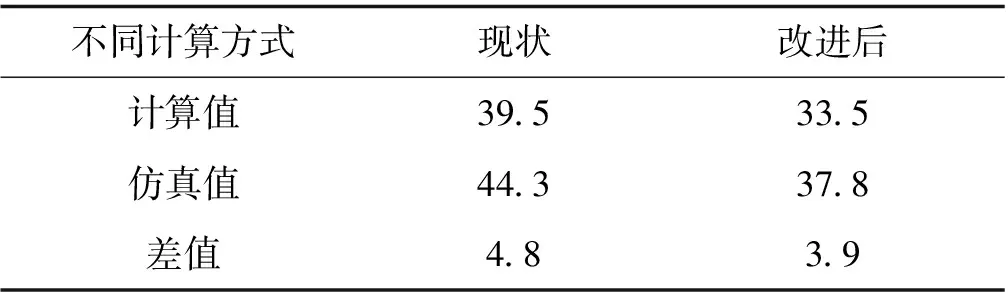
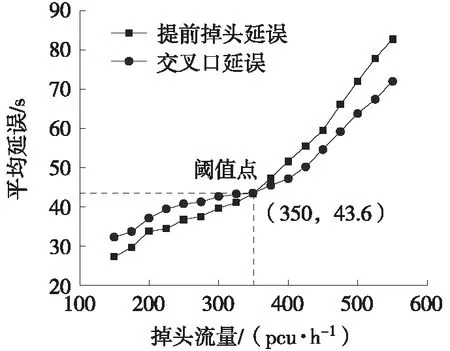
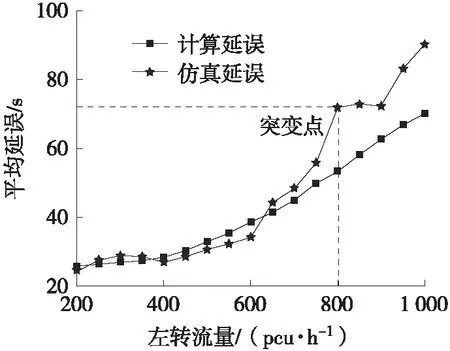
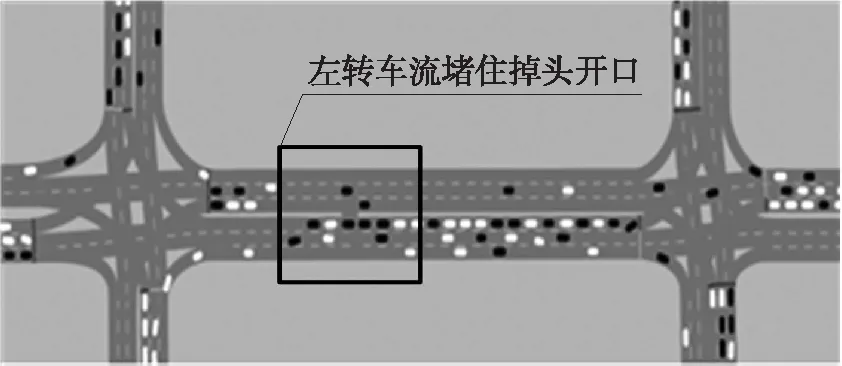
分析可知，当tf

在左转相位开始后，根据驾驶人习惯，还未完成调头的车辆，通常情况下会等待直行相位的最后1辆车通过冲突点后才会进行掉头[7]。因此，直行相位最后1辆车通过掉头口的时间加上左转车启动损失时间(一般取2 s)就是左转车辆等待掉头车驶离的损失时间，即

(13)

式中：tl为左转车辆等待掉头车驶离的损失时间，s；L6为下游交叉口与本向出口道停止线之间的距离，m；vs为直行车辆通过交叉口的速度，m/s。

被调头车辆阻挡的最前1辆左转车通过空余路段的时间(tzl)为：

(14)

式中：φ为左转相位开始时L2上的左转排队车辆数。

则调头车阻挡左转车产生的总损失时间为：

(15)

由于左转车辆在L2上的排队长度不确定，因此所求左转车辆的延误应该是不同排队长度下损失时间的加权平均数[13]。左转车被调头车阻挡的概率为：

(16)

式中：μ为左转车与调头车的比例。

理论分析可知，L2上左转排队车辆数取值范围为0～φmax(φmax=L2/lt)，则掉头车阻挡左转车的延误为：

(17)

掉头及左转共用车道总延误为：

(18)

车均延误为：

(19)

式中：Q1为左转及掉头共用车道每小时总流量。

当路段不设掉头开口，即车辆采用交叉口掉头时，可利用韦伯斯特延误公式来计算交叉口的总延误：

(20)

式中：Dwbster为交叉口总延误；N为交叉口的总车道数；c为交叉口的周期时长；λi为对应相位的绿信比；yi为对应车道的交通流量比；xi为对应车道的交通流量饱和度；qi为对应车道的交通流量。

车均延误为：

(21)

式中：Q2为交叉口每小时的总流量。

3 实例应用及仿真分析

3.1 参数调查与计算

以曲靖市麒麟南路—胜峰路和麒麟南路—文昌街之间的路段为例，如图1所示，计算2种掉头方式的车均延误，得出左转及掉头阈值流量，并验证上述方法的准确性。调查可知，该路段为具有中央隔离栏的双向6车道，每条车道宽3.5 m，掉头开口距离上游交叉口L1(麒麟南路—胜峰路)310 m，距离下游交叉口L2(麒麟南路—文昌街)270 m，L6=63 m，左转车与调头车的比例μ=2.6，下游交叉口周期为170 s，相位时间如表1所示，高峰小时流量如表2所示。

表1 信号配时方案 s

表2 高峰小时流量 pcu/h

结合表2数据，通过Erlang分布拟合对向冲突车流车头时距，并采用χ2检验，得到车头时距t的概率密度函数为P(t)=0.50e-0.50t·0.50t。代入式(3)得到路段掉头开口服务率u=237 pcu/h，由式(4)求得高峰时期掉头口平均排队车辆数为3.30 pcu，即路段掉头口需满足4辆车排队为30 m，再由式(6)求得停车视距LT=45 m，因此LT+LP=75 m，由于L1的取值要略大于LT，这里L1取80 m，并由式(8)求得下游交叉口功能区长度为143 m，满足掉头口设置条件。

因此，将掉头开口由原来距离上游交叉口310 m改为80 m，采用前述车均延误计算公式对比分析改进前后情况，并进行仿真验证，结果如表3所示。对比结果表明，将掉头开口位置提前后，路段通行效率有明显改善。

表3 掉头位置改变前后不同计算方式下的车均延误对比 s

3.2 阈值条件分析

能否提高车流运行效率是判断路段提前掉头设置合理性的关键指标，通过对路段车均延误的计算，可得设置提前掉头的流量阈值判别模型：

(22)

为得出提前掉头设置阈值流量，分别计算2种掉头方式的车均延误，以下游交叉口西进口为例，对向直行车流采用高峰小时流量(1 126 pcu/h)计算。

1) 采用掉头流量(199 pcu/h)不变，增加左转流量，计算2种方式的车均延误，结果如图3所示。

由于车辆在路段中就完成掉头，可减少掉头车辆的绕行时间，从而将有效减少路段车均延误；但随着左转车辆的不断增加，路段延误不断累积，当左转流量增加到550 pcu/h时，此时2种掉头方式的车均延误相同，当再增加左转流量时，提前掉头将不再具有优势。

图3 左转流量与延误关系曲线

2) 采用左转流量(518 pcu/h)不变，增加掉头流量，计算2种方式的车均延误，结果如图4所示。

图4 掉头流量与延误关系曲线

由图4可知，当掉头车流量不断增加，左转车辆在掉头开口后的排队时间也会不断增加，当掉头车流量大于350 pcu/h时，将会导致左转车在开口处排队数量过大，大幅度增加左转车通过空余路段的时间，从而致使路段延误不断累积。此时采取交叉口掉头更为合理。

以上2种比较方案得出，设置提前掉头的阈值流量分别为掉头车道左转流量小于550 pcu/h、掉头流量小于350 pcu/h。

3.3 仿真验证

采用VISSIM仿真进行可行性验证，对仿真驾驶行为进行参数标定，如表4所示，几何设置参照优化后的路段掉头位置，采用对向直行流量不变，分别增加左转及掉头流量，比较理论模型与仿真结果，如图5所示。

表4 VISSIM模型的参数标定和描述

(a) 左转流量-延误

(b) 掉头流量-延误

由图5可知，当不断增加掉头流量时，仿真结果与理论计算值总体拟合较好；而增加左转流量时，仿真结果与理论值前半部分拟合较好，但当左转流量增加到800 pcu/h附近时，仿真延误出现了突变点。过程分析如下，随着左转流量不断增加，致使左转车流从某一时刻开始在一个周期内不能完全通过交叉口，出现车辆排队现象，当左转流量持续增加以至于左转车排队到掉头开口处时，如图6所示，将会阻挡掉头车辆完成掉头，此时掉头车辆到达过程已不再符合Erlang分布，左转车和掉头车辆的延误同时开始陡增，此时突变点开始出现。

图6 交叉口左转车排队阻塞掉头口位置影响示意

综上分析，理论计算与VISSIM仿真结果基本一致，表明本文提出方法和模型在一定条件下可靠准确。

4 结论

本文以提高道路交通运行安全与效率为目标，提出车辆提前掉头交通组织方式，并与传统交叉口掉头方式相比较，得出设置提前掉头的关键几何参数计算模型和车流量阈值条件。

1) 提出掉头开口与上游交叉口距离应大于车辆最大排队长度与安全停车视距之和，与下游交叉口距离应大于其功能区长度，同时确定了掉头开口长度大小计算方法。

2) 提出提前掉头车流排队延误以及掉头车辆阻挡左转车辆延误计算模型。

3) 采用VISSIM仿真软件进行有效性验证，得出设置路段提前掉头交通组织方案的阈值条件，即在对向冲突车流量一定时，交叉口掉头车道的左转流量小于550 pcu/h，掉头流量小于350 pcu/h。

本研究的不足在于分析掉头车流运行机理时，并未考虑中央隔离栏宽度及车型大小的影响，将在后续研究中进一步分析。