连续配筋混凝土路面温湿翘曲效应的敏感性分析

周 舟， 王骁帆

(浙江数智交院科技股份有限公司， 杭州 310030)

连续钢筋混凝土路面CRCP(Continuously Reinforced Concrete Pavement)是一种不设横向接缝和胀缝的路面结构，并在路面中上部配置了足量的连续钢筋，较传统水泥混凝土路面，可控制横向收缩裂缝的发展。CRCP路面寿命长和强度高，常被用于重载和超重载交通路段。美国、比利时等国家主要将其用于机场道面和高速公路；我国主要将其用于高速公路的桥隧路段和重载交通的国省道干线[1]。刘朝晖、黄志义和黄晓明等[2-4]围绕温度效应，研究了CRCP路面的配筋机理和配筋形式，提出了适用于我国的配筋设计理论。高原和Janssen等[5-6]围绕湿度效应，提出了水泥混凝土板的湿度翘曲变形理论。王骁帆和左志武等[7-8]依据裂缝开裂的分布形式，提出CRCP路面结构设计的关键是控制横向裂缝的间距和宽度。上述学者的研究成果，为我国CRCP路面结构设计奠定了理论基础。但根据实际应用反馈，国内CRCP路面使用寿命较短，表明我国在CRCP路面结构设计时考虑的受力因素还不够全面，不满足我国不同区域的气候和交通特点，需聚焦该路面的开裂破坏机理进一步展开深入研究。

黄仰贤等[9]认为，CRCP路面病害产生的根本原因是环境温湿耦合作用引起的横向裂缝间距不均匀、裂缝宽度过大，当板块间连接作用逐步丧失，车辆冲击荷载产生的路面高压水会不断冲击路面基层引起局部脱空，最终形成冲断破坏。CRCP路面会因环境温度变化而引起体积变形，其中，若季节性温降变化较均匀，则引起混凝土板纵向均匀收缩变形(温缩)；若日温度变化形成深度方向的温度梯度，则引起混凝土板温度翘曲变形。环境湿度变化和基层排水不畅在混凝土板产生非线性湿度梯度，引起混凝土板湿度翘曲变形。CRCP路面结构设计指标为横向裂缝宽度、横向裂缝间距和钢筋应力，现有规范主要考虑温缩和干缩效应对3个指标的影响，较少考虑温湿耦合梯度作用[10-11]。

魏亚[12]研究了水泥混凝土路面湿度翘曲形成机理，提出将湿度梯度等效为温度梯度来研究湿度翘曲变形，这是力学推导的理论依据。Shoukry等[13]认为，混凝土材料的杨氏模量、泊松比和线膨胀系数等参数会随相对湿度而变化，即CRCP的混凝土面板为非均匀板，研究也将CRCP考虑为非均匀带筋混凝土结构。田波等[14]认为，CRCP路面翘曲应力的计算可以沿用水泥混凝土路面翘曲应力的计算公式，这是验证CRCP路面有限元建模合理性的理论依据。张翛等[15]利用二维有限元模型计算了湿度梯度作用下，基层类型对CRCP面层的湿度翘曲应力的影响。二维模型计算速度快，但是和实际结构有一定差距。

本文在前人研究的基础上，综合考虑相对湿度对混凝土材料弹性模量的影响，即假设路面板为性质非均匀的水泥混凝土板块，采用ABAQUS商用有限元软件建立了CRCP路面三维模型，利用弹性薄板理论将湿度梯度转化为等效温度梯度，计算了非均匀板CRCP路面在温度、湿度梯度作用下的翘曲效应，将重点分析相关设计参数对计算结果的影响。研究旨在完善水泥混凝土刚性路面的设计，夯实其设计理论基础。

1 混凝土板湿度翘曲变形理论

1.1 计算思路和过程

本文所用的CRCP模型及坐标系统如图1所示。图1中，B为板宽；假设路面板为2条横向裂缝切割成的独立板，s为横向裂缝间距；h为板厚。

图1 CRCP模型及坐标系

由于湿度梯度为混凝土材料的固有特性，故计算思路为首先利用不加筋、不受任何约束的无限大混凝土板推导其计算公式，再通过有限元软件来计算CRCP的翘曲变形。湿度梯度推导过程如下：

1) 假设混凝土板的体力不计，且不受外部约束，其四周相对于整个面板为次要边界，则x=0和x=s处的剪应力忽略，静力平衡方程(y=0和y=B处的边界条件类似)为：

(1)

式中：σx为垂直于yz截面的应力分量。

2) 根据基尔霍夫假设，γxy为0；根据胡可定律，应力σ-应变ε本构方程为：

(2)

式中：εx为x方向线应变;εy为y方向线应变;σy为垂直于xz截面的应力分量;αm为混凝土的湿度线膨胀系数;E为杨氏模量;v为泊松比;RH为相对湿度。

3) CRCP独立板是一种长度和宽度尺寸大致相当的结构，因此可假设板块中性层沿x、y方向的曲率ρx和ρy相同，弹性薄板变形连续相容方程为：

εx≈εy=εRH=ρ·z+ε0

(3)

式中：εRH为湿度梯度作用下应变沿x、y方向分量；ρ为中性层沿x、y方向曲率；ε0为板内残余应变。

4) 联立式(2)和式(3)，得到湿度翘曲应力的解析公式为：

(4)

式中：σRH为湿度梯度作用下应力沿x、y方向分量。

5) 考虑混凝土材料的非均匀性，即令杨氏模量E、泊松比v和湿度线膨胀系数αm为相对湿度RH的函数，又因RH为z的函数，故E=E(z)，v=v(z)，αm=αm(z)。将它们代入式(4)，再代入式(1)，得到非均匀混凝土板的湿度翘曲应力为：

(5)

(6)

6) 计算湿度梯度作用下，非均匀混凝土板的截面湿度弯矩MRH为：

(7)

温度梯度Te作用下，混凝土板的截面温度弯矩MT为[9]:

(8)

式中：ΔTe为上下板面的温度差值，ΔTe=Te·h；αc为混凝土温度线膨胀系数。

为了求解湿度梯度，假设湿度梯度引起的翘曲变形和等效温度梯度Te引起的翘曲变形相同，即令MRH=MT，则由式(7)和式(8)得出上下板面的等效温度差ΔTe为：

(9)

1.2 计算参数取值

Pickett提出混凝土材料的收缩应变ε与相对湿度RH的相关模型，进而得到湿度线膨胀系数αm与RH的相关关系为：

εRH=αm·RH=6.15×10-3×(1-RH)·(1-VA)n

(10)

式中：n为骨料的收缩限制系数，一般取1.68[13]；VA为骨料的体积率。

Shoukry提出了E、v关于RH(%)的关系式：

(11)

Shoukry试验用的混凝土材料物力性质若不考虑相对湿度，其参数取值可依据现行设计规范[10-11]，取E=28 GPa、v=0.18、αc=7.0×10-6/℃、VA=76%。

因此，只要测得混凝土面板的相对湿度分布规律，即可对等效湿度梯度和等效温差进行计算，为下一步采用有限元建模，研究温湿耦合梯度对非均匀CRCP的影响做铺垫。

1.3 等效温度梯度的计算

将高度0.25 m的标准试件置于密闭环境中养护28 d。为了模拟面层外部干燥、面层外部干燥和基层底部滞水的路面湿度环境。将其上表面暴露在RH=50%的环境下，四周与有机玻璃板接触，底部则分别与水或有机玻璃板接触，再养护28 d，试验过程恒温25 ℃。用温湿传感器采集不同试验条件下得到的RH～z曲线进行回归拟合，联立式(7)、式(9)和式(11)计算MRH、ΔTe和Te；若不考虑RH对材料力学性质的影响，则按文献[12]提供的方法计算MRH、ΔTe和Te。计算结果见表1。

表1 非均匀板和均匀板的等效温度梯度

由表1可知，非均匀板的湿度梯度较均匀板大8%～10%；当基层存在滞水时，湿度梯度会显著增大。

2 有限元响应

2.1 有限元模型

某CRCP实体工程位于公路区划Ⅱ区，结构尺寸为0.25 m CRCP+0.18 m贫混凝土基层，行车道宽度为3.75 m，荷载等级为重载交通，设计横向裂缝平均间距为1 m～3 m。假设模型为CRCP断裂后，横向裂缝与纵向接缝围成的独立板。取长(裂缝间距)s=3 m、宽(单个行车道宽度)B=3.75 m。纵向钢筋为HRB335，直径ds=16 mm。纵向钢筋沿横向排列34根，布置在距板顶1/3处。结构层材料的物理力学参数见表2。湿度梯度按照表1取-40.70 ℃/m，温度梯度按照规范取-28.67 ℃/m，碾压式贫混凝土基层与面层的摩阻系数μ依据现行规范取μ=8.5，Winkler地基的反应模量取110 MPa/m[7]。

表2 CRCP模型参数

2.2 建模过程

采用Abaqus有限元搭建CRCP三维有限元模型。CRCP和基层采用C3D8R单元；钢筋采用梁单元B31，再用Embedded命令嵌入CRCP面层中；网格密度CRCP为0.06 m，基层为0.1 m。

通过拉拔试验表明，钢筋和混凝土之间的粘结力和相对滑移成正比，一般用粘结刚度系数ks表征其正比例系数。有限元建模时，一般在钢筋和混凝土之间插入弹簧单元组来模拟粘结-滑移关系[3-4]。

2.3 计算结果及分析

数值模拟结果表明：主应力云图关于CRC板纵向中线和横向中线对称。因此，取1/4路面板，绘制CRC板顶部的主应力分布，如图2所示。随着临近单元体的钳制力增大，越靠近板中，CRC板顶部的拉应力越大，应力变化率越小；横向裂缝附近钢筋的拉应力受到钢筋端部约束的影响，存在应力极值区域；混凝土翘曲应力的最大值为1.69 MPa，且位于CRC板的中心；相邻裂缝间的中部，混凝土拉应力最大，容易发生二次开裂。

图2 面层主应力分布

2.4 理论验证

当不计自重和四周约束的无限大矩形薄板置于文克勒地基上时，将等效温度梯度和温度梯度代入Westergaard公式，可近似求解有限尺寸板的翘曲应力[9]。式(12)、式(13)为路面板中心点和板边半长(宽)处的最大翘曲应力。

(12)

(13)

式中：Cx，Cy为素混凝土路面板的翘曲应力系数，根据Bradbury曲线[9]取值；ΔTg为上下板面的温差，ΔTg=Tg·h；σ为σx时，C取Cx；σ为σy时，C取Cy。

文献[4]认为CRCP温度翘曲应力可利用同尺寸水泥混凝土板的翘曲应力计算，结果见表3。

表3 有限元计算的验证 mPa

根据表3可知，对于板中点的最大翘曲应力，有限元解和威斯卡特德解的平均相对误差为3.5%，满足工程精度的要求(相对误差<5%)；对于板长(宽)中点的最大翘曲应力，平均相对误差约为8%。越接近板中位置，有限元解的精确度越高，且相对于路面板而言，板边区域的面积所占比例较小。因此，赋予混凝土板温度梯度，利用有限元法分析CRCP的温湿耦合翘曲合理可行。

3 配筋设计的敏感性分析

CRCP路面的配筋指标主要有钢筋应力、横向裂缝间距和缝隙宽度三大指标。根据粘结滑移理论和对称性，CRCP路面横向裂缝缝隙宽度是该位置混凝土板位移(缝隙位移)的1.4～2.0倍[1-3]。本文研究了钢筋弹性模量、纵向配筋率和粘结刚度对配筋指标的影响，敏感性分析的基本参数与表2一致，工况采用外部干燥+底部浸湿。当研究某一参数敏感性时，赋予该参数不同的取值，其他参数保持不变。

3.1 纵筋弹性模量和配筋率的影响

分析温湿耦合梯度下，不同配筋材料弹性模量Es对最大拉应力和缝隙平均位移的影响。取纵筋直径ds为11 cm～18 cm，模拟纵向配筋率0.33%～0.89%的工况。CRCP的纵向配筋一般采用HRB钢筋(210 GPa和200 GPa)、BFRP玄武岩纤维筋(50 GPa)和GFRP玻璃纤维筋(40 GPa)。将上述参数代入有限元模型进行计算，结果如图3、图4所示。

图3 纵筋模量对最大拉应力的影响

由图3、图4可知：在温湿耦合梯度作用下，纵筋的弹性模量越小，筋材和混凝土的拉应力越小，缝隙平均位移越大；筋材的最大拉应力随纵向配筋率的增大而减小；混凝土的最大拉应力随纵向配筋率的增大而增大。取Es=200 GPa，ks=28 MPa/mm，当纵向配筋率由0.33%变化到0.89%时，钢筋的最大拉应力减小了41%，混凝土的最大拉应力增大了29%；钢筋埋深处缝隙的平均位移在0.45 mm和0.60 mm之间波动，翘曲变形的总趋势随着纵向配筋率增大而减小。由于BFRP筋和GFRP筋弹性模量较小，且耐腐蚀性能好，因此，它们不仅能减小翘曲效应对结构应力的影响，而且无需考虑缝隙宽度增大而引起的筋材锈蚀。从控制翘曲变形角度看，BFRP筋和GFRP筋是理想的钢筋替代材料。

3.2 粘结刚度系数的影响

以ds=16 cm，Es=200 GPa为例，ks取20 MPa/mm～34 MPa/mm，对CRCP最大应力和缝隙位移进行计算，结果如图5、图6所示。

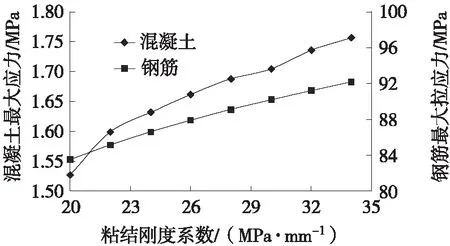
图5 粘结刚度系数对最大拉应力的影响

图6 粘结刚度系数对缝隙平均位移的影响

由图5、图6可知：温湿耦合梯度作用下，当ks由20 MPa/mm变化到34 MPa/mm时，钢筋的最大拉应力增加了10%，混凝土的最大拉应力增大了15%；钢筋埋深处缝隙的平均位移随ks的增大而减小，但是幅度不明显。粘结强度与保护层厚度、混凝土强度和钢筋表面螺纹形式等密切相关，在进行配筋时，需要选用合适的材料来减小温湿翘曲的不利影响。

4 结论

1) 推导了非均匀自由板湿度翘曲应力的解析公式，给出了等效负温度梯度计算方法。相同湿度条件下，非均匀板的等效温度梯度比均匀板大 8%～10%。底部浸湿后，非均匀板的等效温度梯度比仅考虑外部干燥的等效温度梯度大1倍。

2) 将温湿耦合梯度转化为等效温度梯度，代入威斯特卡德公式和有限元模型，用威斯特卡德公式验证了有限元建模合理。

3) 弹性模量较小的GFRP筋和BFRP筋可减小温湿翘曲的不利影响。配筋率由0.33%变化到0.89%时，钢筋的最大拉应力减小了41%，混凝土的最大拉应力增大了29%。当粘结刚度系数由20 MPa/mm变化到34 MPa/mm时，钢筋的最大拉应力增加了10%，混凝土的最大拉应力增加了15%。