拟人服务机器人运动学解耦算法研究

张 刚，布 挺，赵 冰，张 速

（1.洛阳理工学院电气工程与自动化学院，河南 洛阳 471000；2.郑州工程技术学院信息工程学院，河南 郑州 450044；3.河南省嵌入式技术应用工程技术研究中心研发部，河南 洛阳 471003；4.华北水利水电大学信息工程学院，河南 郑州 450046）

服务机器人相较于工业机器人，对使用的安全性与机械结构的紧凑性的要求更高。由于服务机器人无法如工业机器人提供独立的安全保护区域，所以机器人臂长的限制与末端集成度的要求就显得尤为重要。为确保机器人手臂运动的迅速与准确，运动学问题是要解决的核心点。截至目前，学术界通过大量的实验对机械臂的运动学进行了分析与研究。例如，Qiao 等［1］在逆运动学解耦运算过程中使用矩阵的奇异值分解法，针对高阶系统的情况进行了优化。赵铁军等［2］针对冗余7 自由度机械臂的工作空间进行了研究，对比了2种典型冗余自由度手臂，阐述了各自的特点。Grudic 等［3］提出了一种数值迭代方法，通过构建机械手三元运动学方程组，解决了逆运动学求解问题，限于迭代法的本质缺陷，在奇异点附近，雅克比矩阵不可逆或变为病态矩阵的问题没有得到解决，导致迭代无法进行［4］。Wei［5］提出了一种基于模糊系统对机械臂进行运动学建模的方法，同时利用仿真实验验证了理论的正确性。文献中所阐述的方法，针对7 自由度冗余机械臂的效果不理想，无法稳定地提供运动学解耦逆解，特别是对于冗余关节的处理，多数采用记录该关节为特征值的方式，对于视觉伺服系统和连续轨迹跟踪等使用环境，无法从传感器获取关节的特征值，导致方法的使用范围被限制在示教的层面。本文提出的三层BP 神经网络结合解析解法的方式，兼顾了速度与稳定性，通过控制神经元数量的方式避免了大规模使用神经网络在全局最优问题处理时开销过大，而造成系统的实时性负担。

本文将神经网络应用于6 自由度串联机器人的逆运动学，将逆解过程转化为网络权值的训练；以拟人服务机器人为研究对象建立数学模型，采用海量数据对网络进行训练；提出了一种用于冗余机器人逆运动学计算的递归神经网络，提出的递归神经网络基于自反广义逆问题，通过减少需要求解的矩阵方程数量和物理实现的复杂性，简化了伪逆的计算。该递归神经网络具有渐近稳定性，可用于求解冗余机械手的逆运动学问题。最后，用Matlab对该方法进行了分析，结果表明，利用神经网络可以快速有效地求解运动学逆问题。

1 机械结构分析

图1 为最新研发的拟人服务机器人样机，主要分为2自由度头部、7自由度的拟人双臂以及由2个主动轮和3个从动轮构成的移动底盘。

图1 拟人服务机器人Fig.1 Humanoid service robot

为平衡机器人手臂与本体的长度与重量，使得机器人工作更加协调、稳定，机械臂设计方案中采用高集成度末端［6］。如图2 所示，机械臂的肩部到肘部为4个自由度，手腕部有3个自由度，工具为拟人抓手。

根据机器人手臂的结构特点，研究过程中将手臂拆分为2 部分进行建模。本文对几何约束下的仿人机器人手臂进行了运动学分析，在没有方向信息的笛卡尔坐标位置变量下，可以解析得到仿人机器人手臂的所有关节值。该方法特别适用于仿人机器人手臂结构的关节控制。将极坐标选取在机器人手臂的根部，考虑到该机器人左右2 个手臂的对称分布特性，仅求解一条手臂即可等效映射于另一臂。

2 拟人臂的运动学模型构建

本文通过MDH 方法对拟人机械臂进行建模［7］。针对前四轴和腕部三轴的机构分别建立了连杆坐标系，其坐标系分布如图3所示。

图3 连杆坐标系分布Fig.3 Linkage coordinate system distribution

腕部机构的根部固接于第四轴末端，两者运动学的合成即为总运动学正解。

2.1 机械臂运动学正解

在机器人学中，运动学正解是建立从各伺服电机的角度到末端执行器的空间位姿映射的过程［8］。首先利用MDH 方法建立前四轴运动学关系，在此基础上通过变换矩阵的连乘来建立机器人末端执行器坐标系相对于机器人基础坐标系的数学模型转换关系，记为坐标变换矩阵：

机器人的运动学建模过程主要依赖于式（1）中的矩阵。MDH的参数如表1所示。

表1 MDH参数Tab.1 MDH parameters

根据上述参数可以得到各个关节之间的变换矩阵为

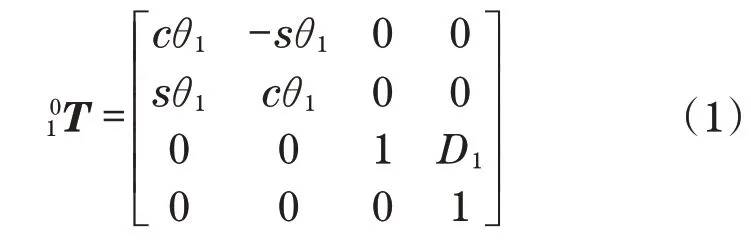
最后，得到4个连杆坐标变换矩阵的乘积：

式中：

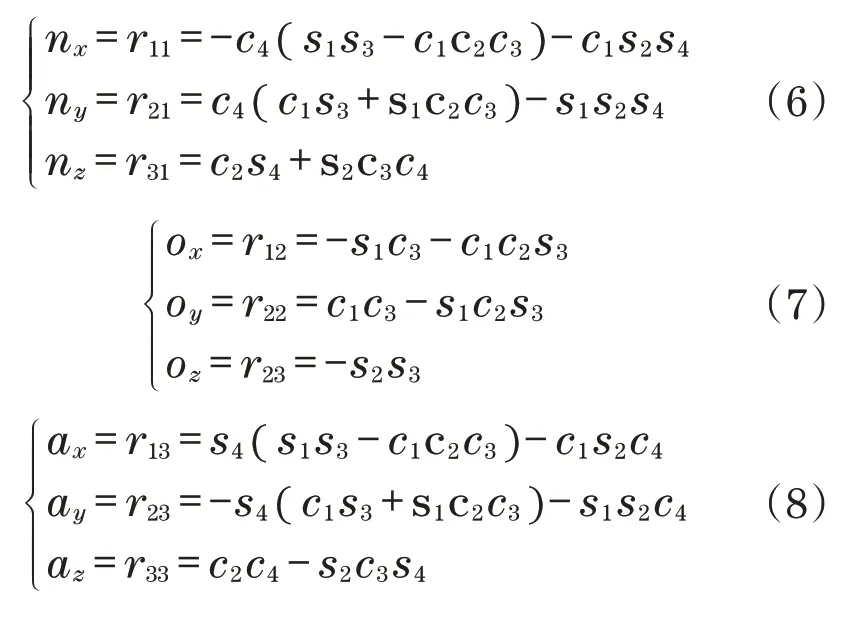
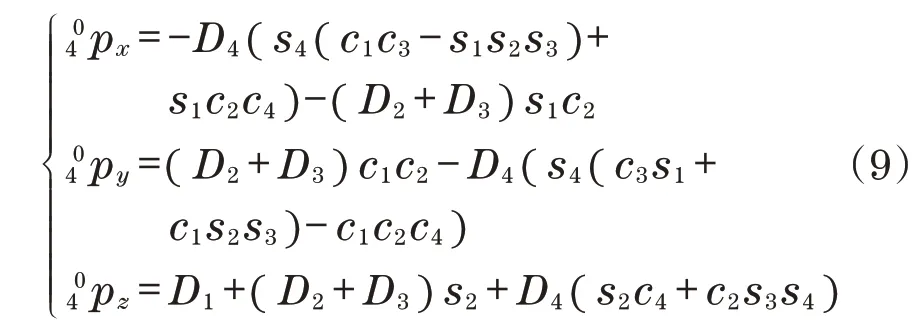
腕部关节齐次变换矩阵如下：

由于腕部仅改变姿态，可得

由式（18）可验证，手臂的大臂与腕部关于末端位置与姿态是解耦的，这是本类型机械臂，逆运动学求解的最重要理论前提，也是设计机械臂的机械结构时主要考虑的因素之一。

2.2 机械臂运动学解耦

机器人拟人手臂的运动学解耦即为逆运动学［9］。机器人逆解过程中，需首先求解前四轴，依据前四轴确定末端位置，后三轴仅影响末端姿态的运动学解耦特性，方便对求解的方程进行降维，可有效提高求解过程的收敛速度，提高求解的稳定性［10］。本文提出了一种求解拟人7 自由度机器人逆运动学的新方法，采用MDH 法求解机器人正运动学解。该方法将机器人的位置与姿态分离与代数迭代相结合，将7 自由度机器人的逆运动学解转化为4 自由度机器人的位置冗余问题。利用Matlab 软件编程实现了机器人关节运动的仿真。该方法计算量较小及实时控制及工业机器人控制。

2.2.1 求解前四轴

由于运动学方程为超越方程且具有较多的自由度，通常采用迭代方法进行求解。其中求解方程的全微分时运算开销较大，且难以保证收敛速度，且传统的牛顿迭代法无法解决方程数少于未知数个数的问题；若采用解析法，同样无法解决上述问题，且解析计算过程中奇异点附近的逆解无法计算，求得部分中间变量为无穷大，导致机器人电机飞车，加剧机器人本体的磨损，降低机器人的寿命［11］。针对这一关键问题，将神经网络理论应用于机器人运动学理论中，学习精度变换。该神经网络根据精确的数据训练，这些数据描述了实际机器人的运动学。该网络通过学习关节角度的差异，提高了理论计算的关节角度与期望端点之间的精度。神经网络可以提高机器人的定位精度和位置重复性。神经网络的应用通过其涌现的泛化、容错和自组织特性，降低了为新机器人开发控制器所需的计算能力、校准时间、维护成本和工程时间。

设N个样本为(Pj，αj)，其中j=1，2，…，N。Pj为网络输入向量，作为第j个位置样本，αj作为第j个电机转角为网络输出向量。可由如下公式将机器人运动学的非线性映射转换为线性映射：

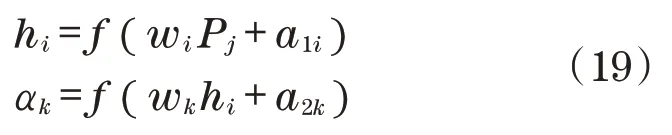
式中：wi、a1i为隐含层的节点i与输入层的权值和阈值；wk、a2k为输出层与隐含层间的权值和阈值。

神经网络拓扑结构如图4所示。

图4 神经网络拓扑结构Fig.4 Neural network topology

提出了一种基于神经网络的拟人服务机器人逆运动学求解方法。本文建立了神经网络来表示末端执行器在正运动学方程中的x、y、z位置。网络结构有4 层：输入层、2 个隐藏层、输出层。输入层和输出层分别定义为机械手角度和末端执行器位置。然后，网络通过学习算法的反向传播对权值进行更新，直到达到网络输出等于期望位置的条件。最后，利用网络的最优权值确定逆运动学解。利用神经网络求解冗余机器人的逆运动学问题，保证了训练过程的收敛性。此外，可以通过增加学习率参数来提高训练速度。该网络使用较低的计算开销，达到了较高的有效性，该算法能够快速、准确地帮助机械手移动到所需要的位置。

2.2.2 求解腕部三轴

由腕部与手臂姿态解耦特征，可解得手腕部3个关节。

根据矩阵方程两边对应项相等可得

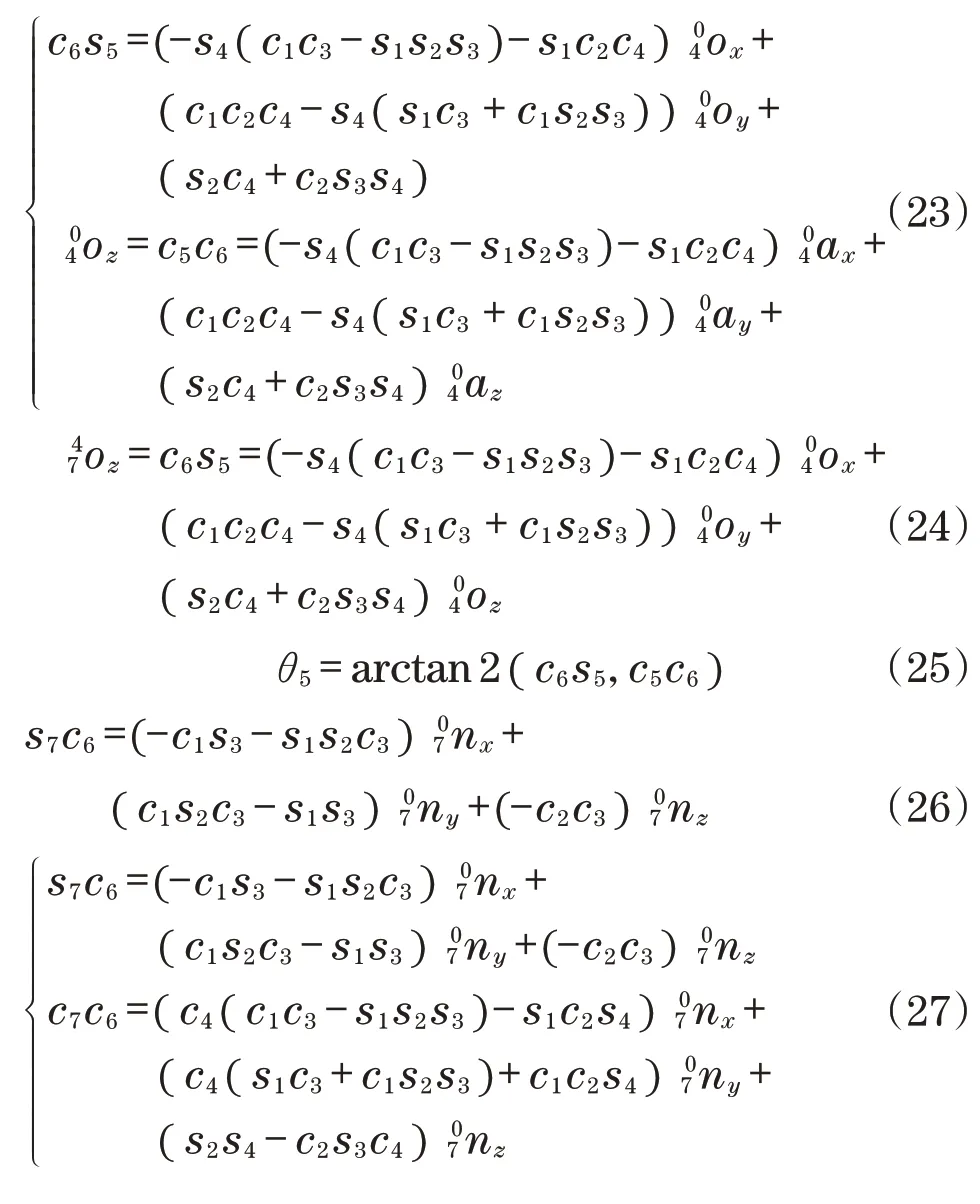
由于正切函数的周期性，机器人关节翻转后可得到第二组解为

角度筛选可依据各关节的象限特征进行，最终获得唯一解。以上为拟人手臂的运动学逆解。

3 仿真与实验

根据机械臂的连杆与高集成腕部的机械参数，通过Matlab 对运动学解耦算法的有效性进行仿真验证。规划机器人末端轨迹曲线，针对曲线上的所有插值点，依次通过解耦逆解得到全部7 个关节值，进而还原机器人末端的空间位置，以此实现对于轨迹的跟踪，其效果如图5所示，其中的2条曲线分别为规划器生成的轨迹曲线和跟踪轨迹时生成的曲线，两条曲线的重合程度可以表示算法跟踪空间位姿的准确性。

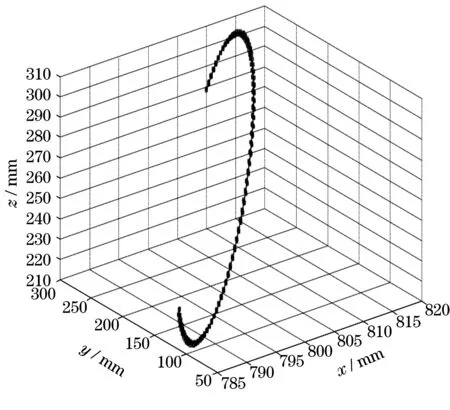
图5 位置跟踪曲线Fig.5 Position tracking curve

从图5 中可得，2 条轨迹几乎重合，证明本算法对于位置的跟踪效果较好。经过统计计算，2 条曲线上对应的插值点偏差样本的均值小于0.001 mm，可以满足服务机器人的实际需要。

通过样机的控制系统总线采集机器人运动过程中7 个关节电机编码器数据，验证解耦逆解算法的有效性。通过示教4 条MOVJ 指令，控制总线采集各个关节的编码器数值，换算为各电机角度，如图6所示。

图6 机器人关节空间曲线Fig.6 Robot joint space curve

从图6 可得，各个关节的空间轨迹连续且平滑，说明解耦逆解算法稳定在大范围内无畸变；关节运动轨迹的起始和结束阶段均为平段，说明所有关节的运动是同步进行的，运算结果会同时体现在各个电机的转角上，也佐证了运动学算法的准确性；曲线的连续、平滑特性说明采集过程中数据更新的实时性较好，验证了运算开销满足总控系统的实时性要求。

4 结语

本文以拟人服务机器人为依托，利用人工神经网络学习机器人手臂的逆运动学进行逆运动学计算，该方法已被许多研究者采用。然而，传统的学习方法对具有冗余自由度的关节典型机器人手臂的逆运动学系统具有无数解，没有很好的解决办法。拟人服务机器人手臂的逆运动学系统是一个多值、不连续的函数，包括具有腕关节的人手臂。本文利用多层神经网络难以逼近该函数，得到正确的末端执行器整体位置和方向的逆运动学模型。针对传统基于解析法逆运动学求解器的不足，提出了一种用于逆运动学模型学习的模块化神经网络结构。在仿真实验部分，通过Matlab 仿真软件，验证了本算法对于连续轨迹的良好跟踪效果；同时为保证论证的严谨性，通过采集机器人总控系统总线中的驱动器编码器信息，绘制了多段运动过程中，各个关节运动的位置轨迹曲线，通过曲线全域连续且平滑，验证了解耦算法可在极大范围内确保逆运动学求解的有效性和稳定性；总线采集数据无较长的水平段，可证明本算法运算速度满足总线传输的周期，满足总控系统的实时性要求。本文针对传统的运动学问题，引入了神经网络来处理多输入多输出的复杂映射关系，改善了逆解的收敛速度过慢以致影响总控系统实时性的问题。目前，研究尚不够完备，后续的研究工作中将针对该类型机械臂的动力学。