利用虚拟杠杆分析复合传动系统无级变速特性方法研究

邹乃威，段传栋，魏建伟，黄元东，王松林，初长祥

（1.宁波工程学院机械工程学院，浙江 宁波 315336；2.柳工机械股份有限公司，广西 柳州 545007）

1 静液-机械复合传动系统

静液-机械复合传动系统先将动力分流成静液传动支路和机械传动支路，再利用行星排的相融耦合特性将静液支路和机械支路的动力进行功率分流传动。

装备静液-机械复合无级传动系统的装载机一般采用类似于图1所示的结构方案。

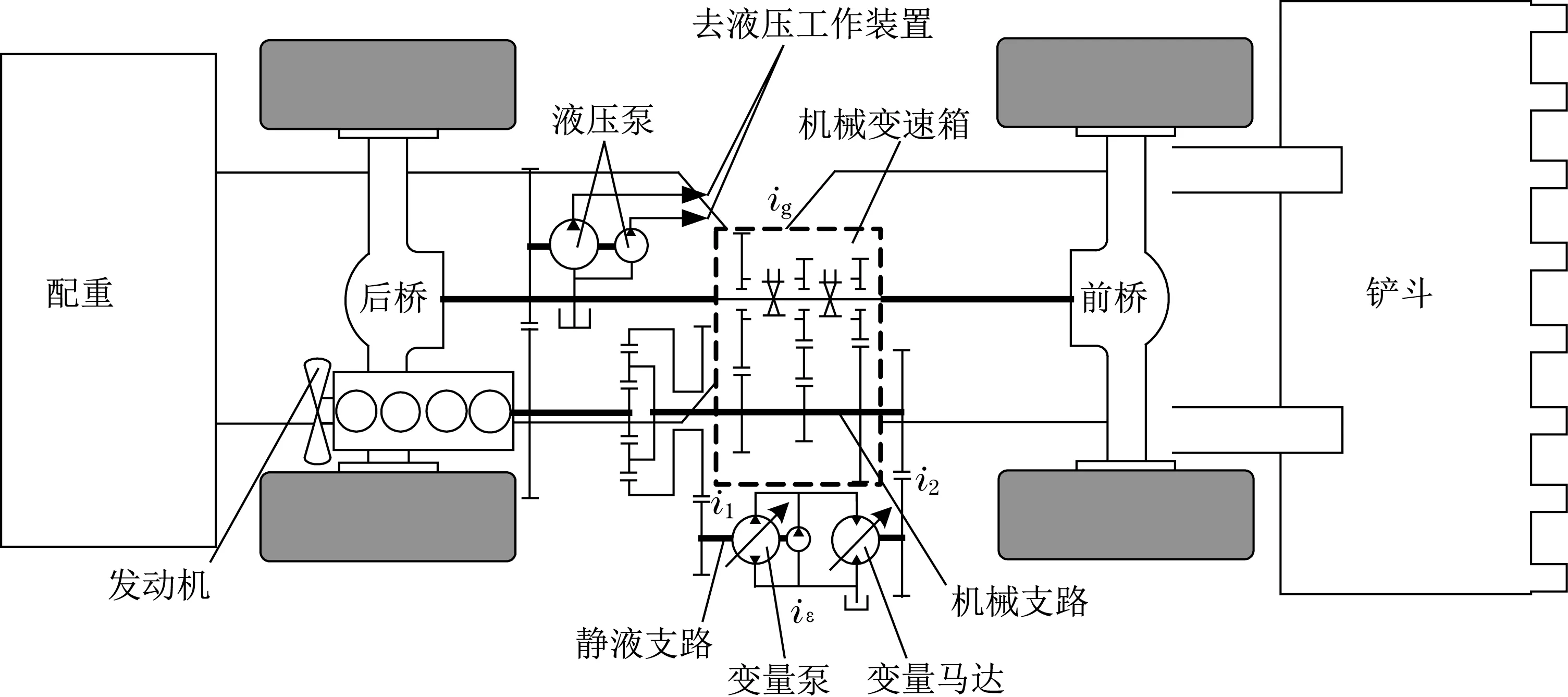
图1 装载机静液-机械复合无级传动方案Fig.1 Wheel loader hydro-mechanical power-split continuous variable transmission scheme

图中：i1为齿圈组件与变量泵输入的速比；i2为静液支路与机械支路汇流齿轮的速比；iε为变量泵与变量马达之间的速比；ig为有级式变速器的阶跃速比。

2 复合传动系统的无级变速特性

2.1 静液支路变速原理

静液支路普遍采用闭式回路，在忽略泄漏损失的条件下，根据闭式回路的流量平衡关系可得

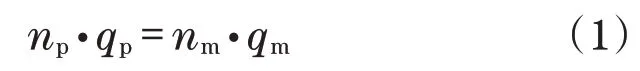
式中：np、nm为变量泵、变量马达的转速；qp、qm为变量泵、变量马达的排量。

变量泵与变量马达的速比、变量泵与变量马达的排量比可表示为

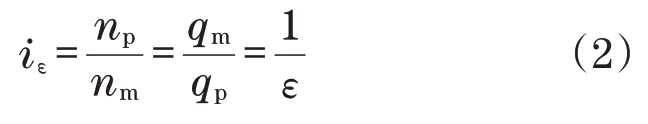
式中：ε为静液传动系统的排量比；iε为静液支路的速比。

式（2）表明了静液支路的速比和排量比呈倒数关系，通过调节排量比即可控制速比。

2.2 行星排相融耦合原理

复合传动系统在静液支路的基础上增加了1条机械支路，以增加其传动功率，拓宽其变速范围，利用行星排将机械支路和静液支路的动力耦合。

行星排各构件之间的转速符合下列关系：

式中：nR、nH、nS分别为齿圈、行星架和太阳轮的转速；ρ为行星排结构参数，其数值等于太阳轮齿数比齿圈齿数。

如图1 所示，发动机动力从太阳轮输入行星排，即发动机转速等于太阳轮的转速：

式中：nE为发动机的转速。

静液支路的两端分别与齿圈和行星架连接，其速比可由变量泵和变量马达的排量比控制，齿圈和太阳轮的转速关系可表示为

式中：i1为齿圈组件与变量泵输入的速比；i2为静液支路与机械支路汇流齿轮的速比；iε为变量泵与变量马达之间的速比。

将式（4）和式（5）带入式（3）得

2.3 虚拟杠杆模型

式（6）中复合传动系统的无级变速特性不够直观，不利于工程分析和设计，本文提出采用虚拟杠杆和数学模型进行配合的方法，分析静液-机械复合传动系统的无级变速特性。

如图2 所示，3 条纵线均表示转速的坐标，且坐标刻度比例均一致，分别表示图1 中的行星排3 个构件的转速和其随静液支路排量比变化的关系。3条纵坐标的相对距离用行星排的结构参数表示，假设行星架转速坐标和齿圈转速坐标的相对距离为ρ（行星排结构参数），则行星架转速坐标和太阳轮转速坐标的相对距离为1，如此排列的3 条纵坐标就能够保持行星排3个构件的转速值始终在1条直线上，仿佛处在1 条虚拟杠杆上［1-3］。在静液支路速比连续变化的情况下，虚拟杠杆法可以用于分析静液-机械复合传动系统无级变速的规律。在图1 所示的传动方案中，在发动机（太阳轮）转速不变的情况下，静液支路变量泵P（齿圈）在静液支路排量比控制下从负的最高转速，经过0 转速，连续增长至正的最高转速时，输出轴（行星架）转速从0（①）连续增大到某一转速（②），即实现了装载机的无级变速传动。

图2 静液-机械复合传动系统行星排耦合关系Fig.2 Planetary scheme coupling relationship of hydro-mechanical power-split continuous variable transmission

2.4 分段无级变速特性

为了进一步降速增扭，拓宽无级变速范围，在行星架的下游还可以串接1 个机械变速器，拓宽静液-机械复合传动系统的变速范围，即在图2所示的①～②的基础上继续拓宽。

计入后续变速传动系统的速比可得总速比为

式中：ig为有级式变速器的阶跃速比；i0为主减速器的固定速比。

由式（7）可知，静液-机械复合传动系统的总速比i∑随iε和ig变化。其中，iε为由静液支路的排量比确定的无级传动速比，在一定范围内可连续变化，使总速比i∑具有无级变速特性，且其变速区间比iε小，如图1 所示；ig为阶跃速比序列，其速比改变将使总速比i∑的变速区间拓宽，如果iε能够使i∑的连续变化区间刚好能衔接上因ig取值变化而使i∑变速区间变化的跨度，则复合传动系统将呈现分段无级传动特性。

静液-机械复合传动无级变速系统的总速比i∑随iε和ig两个变量变化，不同ig值表示机械变速的传动路线不同，对应不同的无级变速段，各段的总速比i∑的解析表达式不同，可统一写成

式 中：iε={x|iεmin≤x≤iεmax，x∈R}，其 中，iεmin、iεmax分别为静液支路速比的最小、最大值；ig={x|x=igⅠ，igⅡ，…，igN且igⅠ＞igⅡ＞，…，＞igN，x∈R}，其中，igⅠ，igⅡ，…，igN为机械速比序列。

为了满足总速比i∑连续变化的条件，相邻速比段的取值区间应该无断点，即相邻2 段的速比满足：

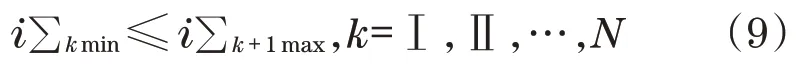
式中：i∑kmin为k段最小速比；i∑k+1max为k+1 段最大速比。

2.5 换段的连贯性

由式（8）可知，总速比i∑无级变速区间受iε的变速范围限制，通过机械支路的切换使iε能够重新开始拥有变速区间，使i∑在更广阔的区间内保持无级变速特性，这个过程称之为换段。换段有2 种方案：①连贯式换段，要求静液支路的速比iε（排量比）向相反方向变化，如图3（a）所示［4］，通过改变总速比i∑的函数关于静液速比的单调关系继续保持总速比i∑的变化趋势，换段前后应满足

②复位式换段，要求保持原总速比i∑函数和静液速比iε的单调关系，在切换变速段时迅速将静液支路的速比iε（排量比）复位以继续保持总速比i∑的变化趋势，如图3（b）所示，换段前后应满足

图3 静液-机械复合传动的速比合成关系Fig.3 Ratio composition relationship of hydro-mechanical power-split continuous variable transmission

3 实例分析

3.1 HVT R2的变速传动特性

德纳-力士乐的HVT R2传动方案［5］如图4所示［6］。ZR、Z0～Z9均为啮合齿轮；CR、C1～C3均为湿式多片离合器。

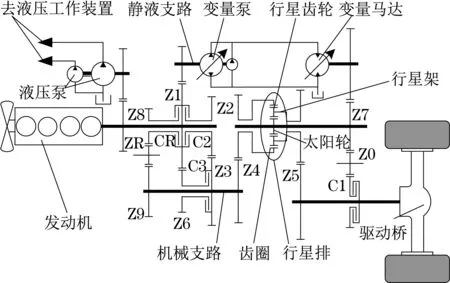
图4 德纳-力士乐HVT R2的结构方案Fig.4 Structural scheme of Dana-Rexroth HVT R2

3.1.1 传动路线及控制逻辑

HVT R2 共有3 个前进挡和2 个倒挡。当离合器C1结合时，HVT R2工作于纯静液传动的第1段，通过液压换向实现前进和倒退挡的切换，即HVT R2 的前进和倒退不需要操作离合器；当离合器C2结合时，HVT R2工作于复合传动的第2段；当离合器C3结合时，HVT R2工作于第3段；当离合器CR 结合时，HVT R2 工作于复合传动的倒挡2 段。HVT R2的离合器控制逻辑如表1所示［7］。

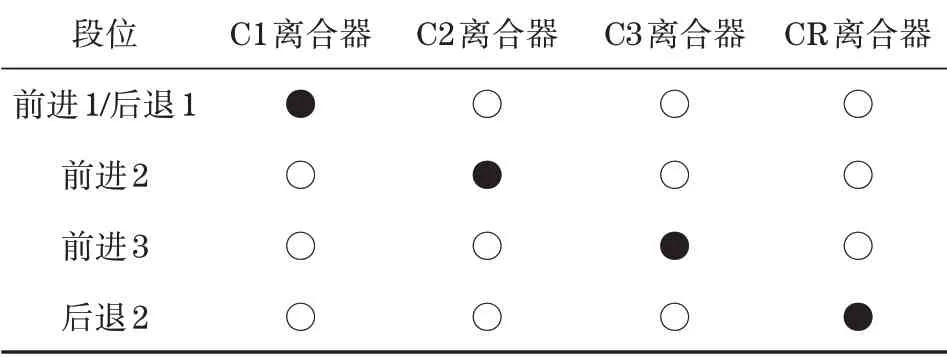
表1 HVT R2的段位与离合器结合状态表Tab.1 HVT R2 stage and clutch engage state

3.1.2 无级变速传动特性分析

图4 为HVT R2 结构方案。静液支路和机械支路的转速耦合关系如图5 所示。行星排的太阳轮和变量马达连接，太阳轮转速坐标正比于静液支路变量马达M 的输出转速，变量马达M 的输出转速应在一定范围内关于0 对称，在HVT R2 的每个变速段中太阳轮的转速可以在这个区间内连续变化；机械支路动力从齿圈输入行星排，即发动机转速正比于齿圈的转速，假设发动机转速在HVT R2 变速过程中转速不变，则对应于第2 段和第3 段齿圈的输入转速分别为K1·nE和K2·nE。当HVT R2 处于2 段时，静液支路变量马达M 的输出转速从负的最高转速变为正的最高转速，行星架上耦合后的转速由①连续变化到②；当HVT R2 处于3 段时，变量马达M 复位后的输出转速再从负的最高转速变为正的最高转速，行星架上耦合后的转速由③连续变化到④。

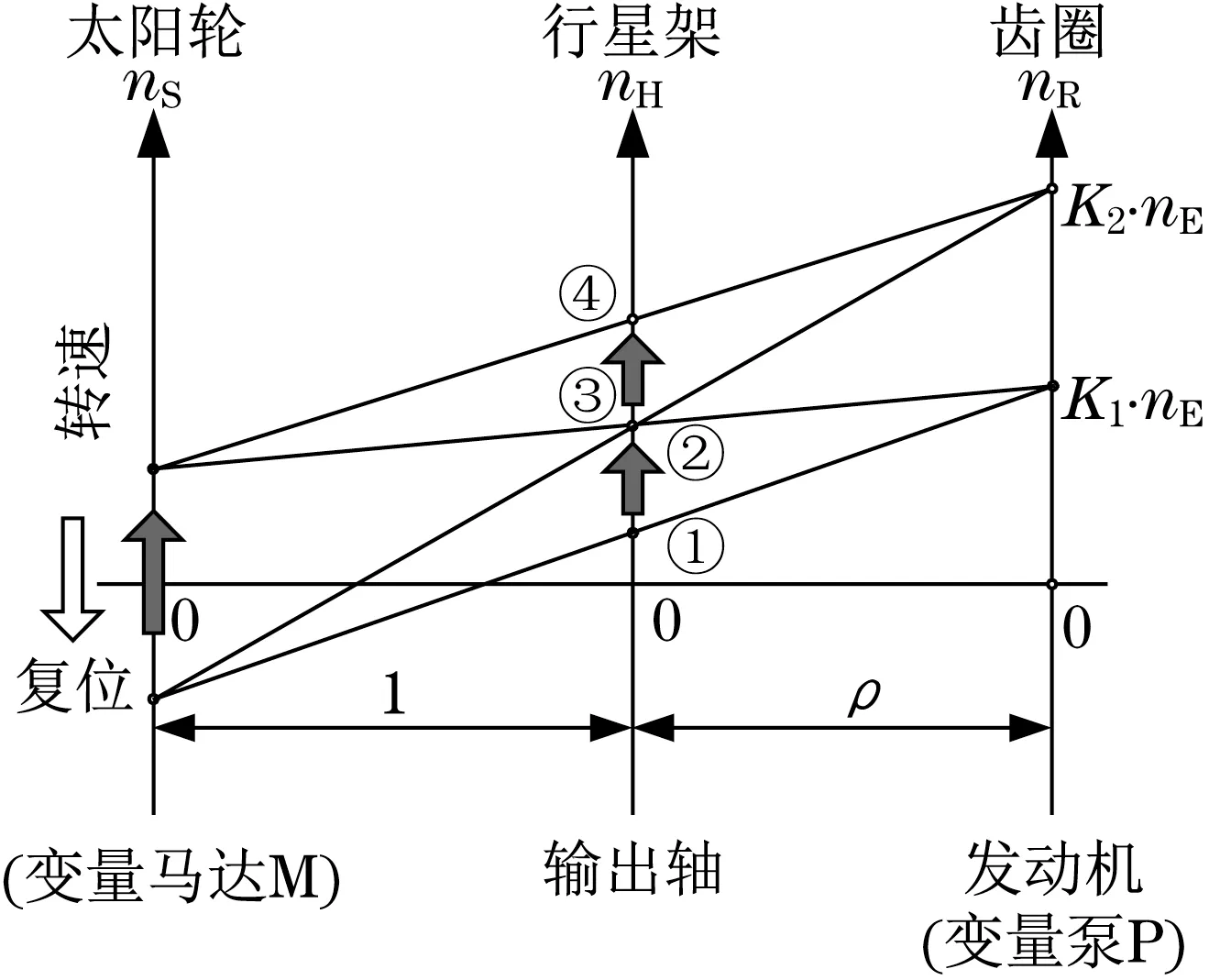
图5 HVT R2的行星排耦合关系Fig.5 Planetary scheme coupling relationship of HVT R2

如果HVT R2 的第1 段中静液支路的变速范围刚好和①衔接，且②和③刚好衔接，则HVT R2的整个变速输出区间是连续的，即满足式（9）。

当车辆起步时，变量马达M 先从0 变到负的最高转速（HVT R2处于第1段），输出轴转速由0连续升高到①，变量马达M从负的最高转速变到正的最高转速（HVT R2 处于第2 段），输出轴转速由①连续升高到②，变量马达M 复位，再次从负的最高转速变到正的最高转速（HVT R2 处于第3 段），换段过程满足式（11），该换段过程属于复位式换段，对传动系统冲击较大，输出轴转速由③连续升高到④，如图5所示。

3.2 cPower的变速传动特性

采埃孚的cPower 的传动方案如图6 所示［8］。Z1～Z10 均为啮合齿轮，CR、CF、C1、C2 均为湿式多片离合器。

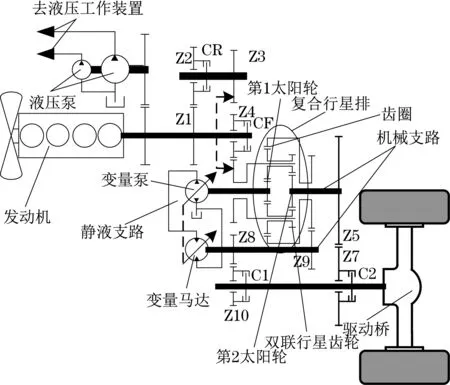
图6 采埃孚cPower结构方案Fig.6 Structural scheme of ZF cPower

3.2.1 传动路线及控制逻辑

cPower 的前进和倒退采用前离合器CF 和倒挡离合器CR 控制。当前进离合器CF 和C1 结合时，cPower 工作于第1 段。第1 段对应的车速较低，和装载机的作业车速相对应，因此传动路线较短，传动效率较高。

当前进离合器CF 和C2 结合时，cPower 工作于第2 段。第2 段对应的车速较高，装载机较少使用，因此传动路线较长，传动效率较低。

当倒挡离合器CR 结合，再配合相应段位的离合器，cPower 就实现了相应挡位的倒挡，cPower的离合器控制逻辑如表2所示。

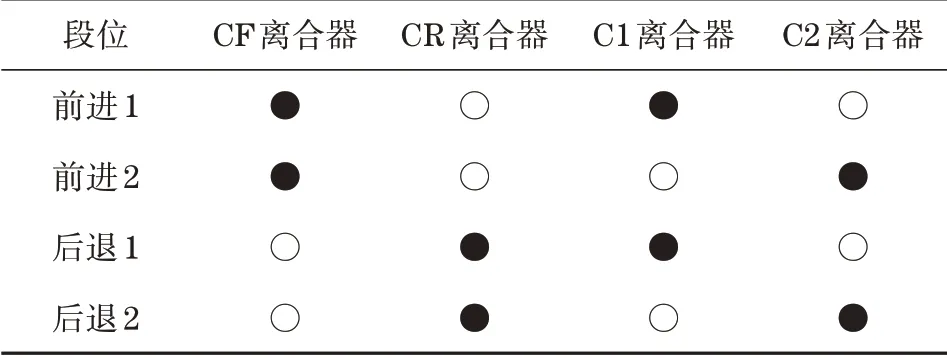
表2 cPower的段位与离合器结合状态表Tab.2 cPower stage and clutch engage state

3.2.2 无级变速传动特性分析

cPower中的复合行星机构共有4个端口，图7中的4条纵坐标分别表示每个端口所代表构件的转速，运用行星排虚拟杠杆法建立各构件的转速关系，其中第2太阳轮转速轴和行星架转速轴之间的距离用β表示，即前行星排与后行星排的转速相关关系［9］。

当cPower处于第1段时，第1太阳轮和变量泵P 连接，齿圈和变量马达M 连接，同时连接cPower的输出轴，行星架和发动机连接，因为变量泵P 和变量马达M 以45°相位差共轭固连，致使泵P 和马达M 的排量始终呈反相位相关变化，即泵P 的排量增大，则马达M 的排量较小，反之亦然。假设发动机（行星架）转速不变，通过调节变量泵P 和变量马达M 的排量，引起变量泵P（太阳轮）的转速从高变到低，变量马达M（齿圈）的转速从低变到高，使cPower 的输出转速由①连续增加到②，如图7（a）所示。

当cPower处于第2段时，第1太阳轮和变量泵（用作马达M）连接，齿圈和变量马达（用作泵P）连接，行星架和发动机连接，cPower的输出轴和第2太阳轮连接。此时，变量马达（用作泵P）的转速较高（延续第1段的工作状态），变量泵（用作马达M）的转速较低（延续第1段的工作状态）。假设发动机（行星架）转速不变，通过反向调节变量马达（用作泵P）和变量泵（用作马达M）的排量，使变量马达（用作泵P）的转速从高变到低，变量泵（用作马达M）的转速从低变到高，使cPower在第2太阳轮的输出转速由③连续增加到④，如图7（b）所示。

图7 cPower的行星排耦合关系Fig.7 Planetary scheme coupling relationship of cPower

如果适当调整Z5 和Z7、Z8 和Z10 的齿数比，就可以使②转速刚好衔接③的转速，使cPower的整个变速区间连贯，满足式（9）要求。由于cPower第1段和第2段耦合方式不同，传动路线不同，且变量泵和变量马达在换段时功能互换，所以该换段过程属于连贯换段，满足式（10），对传动系统冲击较小。

4 仿真验证

以HVT R2 的传动方案为例，在AMESIM 仿真环境下建立仿真模型。

设计1个从0加速至35 km/h再减速至0的循环工况，期望车速和仿真车速随时间变化如图8所示。

图8 仿真车速与期望车速Fig.8 Simulation velocity and expect velocity

机械传动支路离合器前的Z8 齿轮和离合器后的Z3齿轮的转速变化关系如图9所示。

图9 HVT R2机械支路离合器前后的齿轮转速Fig.9 Gears speed before and after clutches in HVT R2 mechanical branch

受HVT R2 的C1、C2 和C3 离合器结合状态的控制，其行星排3个构建的转速如图10所示。

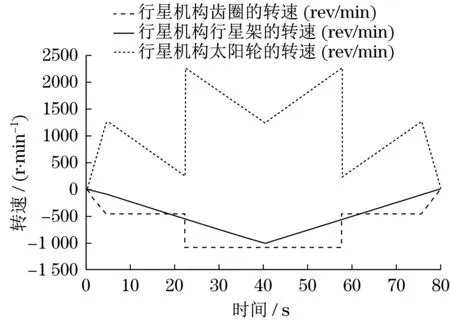
图10 HVT R2动力耦合装置3个构建的转速关系Fig.10 Three components speed relations of power couple set in HVT R2

车速从0到最高车速的仿真过程（0～40 s段）静液支路随着段位的变化：在其变量泵输入转速不变的情况下，在变量泵和变量马达排量比的调节下，变量马达的转速先从0下降，到负的最高转速后，转而上升，越过0点后达到最高转速，后又复位至负的最高转速，随后又逐渐升高至最高转速，在此过程中车速持续升高，直至达到最高车速35 km/h。装载机降速过程和升速过程刚好相反，整个循环工况仿真结果如图11所示。

图11 HVT R2静液支路的输入输出转速Fig.11 Input and output speed relations in hydrostatic branch of HVT R2

HVT R2的总速比由机械支路速比和静液支路速比共同决定，如图12所示。

图12 HVT R2的速比合成关系Fig.12 Speed ratio composed relations of HVT R2

仿真结果再现了HVT R2的复位式换段无级变速特性，在发动机输入转速不变的前提下，车速在离合器和排量比的控制下，装载机实现了从静止到最高车速，再从最高车速减速停车的动态过程，验证了虚拟杠杆法分析结果的正确性和有效性。

5 结语

本文建立了装载机静液-机械复合传动无级变速系统的系列数学模型，并在数学模型的基础上引入了虚拟杠杆模型，全面地描述了该系统的分段无级变速特性，为精确描述静液-机械复合传动系统的无级变速特性提供了方便、有效的方法；利用虚拟杠杆法分析了德纳-力士乐HVT R2 和采埃孚cPower 的无级变速特性，通过仿真模型再现了HVT R2 的无级变速传动特性，验证了虚拟杠杆法的正确性和有效性。