非对称代数Riccati方程的一类不精确迭代解法

王志欣，关晋瑞

(太原师范学院 数学与统计学院，山西 晋中 030619)

1 引言

考虑非对称代数Riccati方程

XCX-AX-XD+B=O,

(1-1)

国内外很多学者提出了许多求解非对称代数Riccati方程的数值解法[5-16]，如不动点迭代法、牛顿迭代法、交替线性化隐式迭代法、保结构加倍算法等.牛顿迭代法和保结构加倍算法是收敛较快的两个算法，在一般情形下具有二次收敛率，但是牛顿迭代法运算量较大，而保结构加倍算法运算量较小，因此保结构加倍算法是求解非对称代数Riccati方程的一类较好的算法.交替线性化隐式迭代法虽在一般情形下具有线性收敛率，但是在迭代过程中运算量小，因此交替线性化隐式迭代法是线性收敛方法中较好的一类算法.不动点迭代法形式简单，在一般情形下也具有线性收敛率，但是在每步迭代中一般需要求解一个Sylvester矩阵方程，运算量比较大，并且它的收敛速度相比于其它算法也较慢，因此不动点迭代法存在很大的改进空间.

本文针对一类常用的不动点迭代法提出了一种改进，其基本思想是通过内外迭代求解以减少运算量.由于不动点迭代法在每步求解Sylvester方程时运算量较大，因此本文提出在每步求解Sylvester方程时使用Smith算法，进而形成一类不精确的迭代算法.这类不精确算法不仅减少了运算量，而且缩短了计算时间.

2 预备知识

本节中，我们介绍一些要用到的符号、术语以及基本概念.

在本文中Rm×n表示所有m×n阶实矩阵，Cm×n表示所有m×n阶复矩阵，O，o，0分别表示零矩阵，零向量，数零，A⊗B表示矩阵的Kronecker乘积，vec(A)表示矩阵A的拉直向量，其中vec(·)称为拉直算子.

若m×n阶实矩阵A=(aij)m×n满足aij≥0(1≤i≤m,1≤j≤n)，则称A为非负矩阵，记为A≥O.若有两个m×n阶实矩阵A=(aij)m×n，B=(bij)m×n满足aij≥bij(1≤i≤m,1≤j≤n)，则记为A≥B.若n维实矩阵A的非对角元素都小于等于0，则称A为Z-矩阵.Z-矩阵都可以写成A=sI-B(s≥0)的形式，其中B是非负矩阵.如果s≥ρ(B)，其中ρ(B)为B的谱半径，则称A为M-矩阵.若有s>ρ(B)，则称A是非奇异的M-矩阵；若有s=ρ(B)，则称A是奇异的M-矩阵.

下面是M-矩阵的一些重要结论.

引理2.1[17]设A=(aij)∈Rn×n是Z-矩阵，则下列条件等价：

①A是非奇异的M-矩阵；

②A-1≥O；

③存在正向量x>o，使得Ax>o.

引理2.2[17]设A是非奇异的M-矩阵，B为Z-矩阵.如果A≤B，则B也是非奇异的M-矩阵.特别地，对任意的正实数α，B=αI+A也是非奇异的M-矩阵.

引理2.3[13]若A是一个非奇异的M-矩阵，选择一个合适的α且满足α>0，定义T(α)=(αI-A)(αI+A)-1，则有

ρ(T(α))<1,∀α>0.

关于非对称代数Riccati方程(1-1)的解，我们有如下结论.

引理2.4[6]若K是非奇异的M-矩阵或不可约奇异的M-矩阵，则方程(1-1)存在唯一的最小非负解X.

下面我们简要介绍求解Sylvester方程的Smith算法[18].考虑Sylvester方程

MX+XN=Q,

(2-1)

这里M∈Rm×m，N∈Rn×n，Q∈Rm×n.选择合适的α>0，可以把(2-1)变为

(αI+M)X(αI+N)-(αI-M)X(αI-N)=2αQ,

上式分别左右乘(αI+M)-1，(αI+N)-1，进而可变成

X-UXV=W,

(2-2)

其中：

U=(αI+M)-1(αI-M),V=(αI-N)(αI+N)-1,

W=2α(αI+M)-1Q(αI+N)-1.

通过计算可得

是Sylvester方程(2-1)的精确解，并且当ρ(U)<1和ρ(V)<1时，这时解是收敛的.Smith提出一种加倍迭代方法：

Xk+1=Xk+U2kXkV2k,X0=W,k=0,1,2,….

(2-3)

进一步(2-3)可以归纳为

在Sylvester方程(2-1)中这个迭代序列{Xk}二次收敛于X*.

3 一类不精确迭代法

本节，我们提出一类不精确迭代法以求解方程(1-1)，并给出此方法的收敛性分析.

文献[6]中提出了一类求解方程(1-1)的不动点迭代法，利用分裂

A=A1-A2,D=D1-D2,

其中：A1，D1为非奇异的M-矩阵，A2，D2为非负矩阵，可以将方程(1-1)写为

A1X+XD1=XCX+XD2+A2X+B,

按照上式迭代求解，便得到如下迭代形式

A1Xk+1+Xk+1D1=XkCXk+XkD2+A2Xk+B,

(3-1)

其中可以选择的几种分裂为

FP1:A1=diag(A)，D1=diag(D)；

FP2:A1=tril(A)，D1=tril(D)；

FP3:A1=A，D1=D.

下面我们仅考虑第三种分裂FP3，因此(3-1)变成

AXk+1+Xk+1D=XkCXk+B,

(3-2)

该方法在一般情形下具有线性收敛率，在临界情况下具有次线性收敛率.由于在每步迭代中都需要求解一个Sylvester方程，这会导致运算量比较大，因此我们考虑在每步迭代求解Sylvester方程时使用Smith算法以降低运算量，进而减少计算时间.

记Qk=XkCXk+B，并选取合适的α>0，我们可以把(3-2)首先变换成

(αI+A)Xk+1(αI+D)-(αI-A)Xk+1(αI-D)=2αQk,k=0,1,2,…,

同样地，上式分别左右乘(αI+A)-1，(αI+D)-1，变成

Xk+1-UXk+1V=Wk,k=0,1,2,…,

其中：

U=(αI+A)-1(αI-A),

V=(αI-D)(αI+D)-1,

Wk=2α(αI+A)-1Qk(αI+D)-1,

因此如果ρ(U)<1以及ρ(V)<1，我们就可以应用双层迭代求解(3-2)，这样就得到了一个不精确的不动点迭代法，其中相应的外层Xk+1是通过内层迭代序列Xk,l得到的，

Xk,0=Wk，Xk,l+1=Xk,l+U2lXk,lV2l，l=0,1,2,….

(3-3)

算法的完整形式如下：

算法3.1 一类不精确迭代法(IFP)

step 1.输入矩阵A，B，C，D，令X0=O，并选取参数εout和ηinn分别为外层不动点迭代法和内层Smith算法的终止条件；

step 2.令k=0，ρ=1；

step 3.计算ρk=‖XkCXk-AXk-XkD+B‖/ρ；

step 4.如果k=0，则令ρ=ρ0；

step 5.如果ρk≤εout，则令X=Xk并且停止；

U=(αI+A)-1(αI-A),V=(αI-D)(αI+D)-1,

Qk=XkCXk+B,Wk=2α(αI+A)-1Qk(αI+D)-1,

step 7.Simth算法

step 7.1 令Xk,0=Wk，εinn=ηinnρk；

step 7.2 计算r0=‖UXk,0V‖；

step 7.3 如果r0<εinn，则令Xk+1=Xk,0并返回；

step 7.4 令l=0；

step 7.5 计算Xk,l+1=Xk,l+UXk,lV；

step 7.6 计算rl+1=‖Xk,l+1-UXk,l+1V-Wk‖/r0；

step 7.7 如果rl+1<εinn，则令Xk+1=Xk,l+1并返回；

step 7.8计算U=U2，V=V2；

step 7.9 令l=l+1，并转至步骤7.5；

step 8.令k=k+1并转至步骤3.

与基本的不动点迭代法相比，这种不精确的不动点迭代法在每步求解Sylvester方程时U,V都是不变的，因此运算量和存储量都会减少.除此之外，我们还注意到，可以改变每一次外部迭代相对应的内部迭代步数，就可以调整其收敛速度，因此，我们提出了有限步不精确的不动点迭代法.

算法3.2 有限步不精确的不动点迭代法(LIFP)

给定一个初始值X0≥O，对于k直到Xk收敛，执行算法3.1，并将步骤7替换为使用k步加倍迭代法来寻找Xk+1，其中Xk+1满足

‖AXk+1+Xk+1D-XkCXk-B‖≤ηinn‖R(Xk)‖.

我们首先证明由算法3.1生成的序列是有界的.

证明使用数学归纳法证明.

由引理2.3知ρ(U)<1，ρ(V)<1，因此可以运行不精确的不动点迭代法.

下证对任意的k≥0，Xk≤X.

当k=0时，X0=O≤X显然成立.

假设结论对小于等于k成立，下面考虑k+1的情形.在k+1次迭代中

因此有

用拉直算子vec(·)作用于方程两端可得

易知A与D都是非奇异的M-矩阵，则(I⊗A+D⊗I)也是非奇异的M-矩阵，所以有

由不精确的不动点迭代法，我们可以得到

从而结论对k+1也成立.由归纳法，任意的k≥0，结论都成立.

其次我们证明由算法3.2生成的序列单调递增并收敛.

O≤Xk≤Xk+1≤X,k=0,1,2,….

证明由算法3.2知

其中U,V是固定的，易用归纳法证得O≤Xk≤Xk+1,k=0,1,2,….又由引理3.1可以得到Xk≤X,k=0,1,2,…，因此由算法3.2得到的序列单调递增有上界.

定理3.3 假设同定理3.2，则由算法3.2生成的矩阵序列{Xk}单调递增收敛于X.

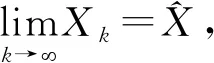
4 数值例子

本节中我们使用几个例子来说明该算法的可行性与有效性，并分别从迭代步数(IT)、计算时间(CPU)以及相对误差(RES)三方面对FP3，LIFP来进行比较，其相对误差为

在我们的实验中，所有算法都是在具有2GCPU和16G内存的个人计算机上进行，并且迭代过程满足RES<10-6时运算终止.

例4.1[14]考虑方程(1-1)，其中

这里K是不可约奇异的M-矩阵且μ≠0.我们分别取n=50,100,500.从表1中可以看出，LIFP算法的收敛时间比FP3的收敛时间小的多.

表1 例4.1的实验结果

例4.2[9]考虑方程(1-1)，其中

A=D=Tridiag(-I,T,-I)∈Rn×n

是块三对角矩阵，

是三对角矩阵，并且

B=SD+AS-SCS

使得

是方程(1-1)的最小非负解，这里

并且n=m2.通过选择不同的m来展示数值实验的有效性，实验结果见表4.2.由表可见，这两种方法都可以求得满足方程精度的解.虽然LIFP的迭代步数比FP3的迭代步数多，但是LIFP的收敛时间要比FP3少.

表2 例4.2的实验结果

通过上述两个例子，我们可以清楚地看到LIFP算法的运算时间远小于FP3，因此本文的改进是很有效的.

5 结论

本文研究了非对称代数Riccati方程的数值解法，提出了一类不精确迭代法以求解方程.该方法在外层迭代中使用不动点迭代法，而在内层迭代求解Sylvester方程时采用了Smith提出的加倍迭代方法，通过内外迭代降低了运算量和存储量，进而减少了计算时间.理论分析和数值实验证实本文的改进是可行的，而且也是较为有效的.