水下爆炸载荷作用下浮体模型变形机理研究

孙远翔，陈岩武，王成，王永强

（北京理工大学 爆炸科学与技术国家重点实验室，北京 100081）

由于水下爆炸问题涉及强非线性、多因素耦合效应，采用数值模拟研究爆炸载荷下舰船板架结构的动态响应较为普遍[1-3]. 能量法作为一种理论分析手段，忽略了中间复杂过程而直接计算最终状态，降低了理论分析的难度. 一些学者使用能量法计算了舰船板架结构在爆炸载荷下的塑性变形能和变形挠度. 对于完全固支边界，一些学者认为作用到板架上的冲击波冲量全部转化为板架的动能，进而全部转化为板架的塑性变形能[4-6]；对于水面浮动边界，王军等[7]用入射冲击波能减去舱段刚体运动动能作为舰船底部板架的塑性变形能.

这些算法一方面忽略了水下爆炸气泡脉动二次加载对板架变形的影响，导致预测值偏小[8]，另一方面忽略了反射冲击波、界面空化现象的影响[9]，导致预测值偏大. 一些学者研究了板架结构对水下爆炸能量的利用率，RAJENDRAN等[10]进行固支圆板水下接触爆炸试验，发现板的塑性变形能只是入射冲击波能的12.36%，近似为一个常数，与冲击环境无关. 汪俊等[11]基于无空化的Taylor平板理论，考虑冲击波与板架的流固耦合作用，建立了板架在爆炸载荷下的吸能模型，发现能量吸收率随流固耦合参数的变化而变化，冲击波能量最多只有54.13%可以被板架所吸收. 可以看出，针对爆炸载荷下板架结构对能量的利用规律，不同学者得到的结论差异较大.

本文设计水面浮体结构模型，通过改变爆距、板厚、药量，对浮体模型在水下爆炸载荷下的运动特征和底部靶板的塑性变形特征进行分析，进而总结舰船底板在水下爆炸载荷下的能量利用规律. 该研究为爆炸载荷下舰船底板的挠度计算和水下武器的高效毁伤提供数据和理论参考.

1 实验研究

1.1 实验概况

本实验在一个直径4 m、深5 m的室内水池中进行. 浮体模型入水示意图如图1所示. 由气背桶、密封垫圈、底部靶板、底部法兰共4部分组成，靶板总尺寸400 mm×400 mm，有效实验区尺寸300 mm×300 mm，靶板材料为Q235钢，密度为7 850 kg/m3，靶板处于背空环境. 使用20个高强度螺栓对模型的4个部分进行组装，组装后的浮体模型总质量为67.42 kg. 关于冲击波载荷的测量，选用聚偏氟乙烯(PVDF)传感器，该传感器曾被成功地用于测量壁面入射冲击波载荷[12]. 本实验首先将PVDF传感器布置在底部靶板上，用于测量靶板受到的入射冲击波载荷，然后将浮体模型吊起，再将炸药固定在靶板正下方一定距离处，整理好传感器和雷管引线. 最后将模型缓慢放入水池，将模型吃水深度控制在0.20 m.

图1 水面浮体模型入水示意图Fig. 1 Floating model entering water

实验工况如表1所示，采用TNT炸药，采用柱状压药的装药方式，装药密度为1.63 g/cm3. 为使TNT炸药的长径比接近1，本次实验采用的10gTNT药柱尺寸为Φ20 mm×21 mm；20g TNT药柱尺寸为Φ25 mm×26 mm；30 g TNT药柱尺寸为Φ30 mm×26.8 mm. 用8号工业级电雷管引爆，雷管的TNT当量按1 g计算，雷管引线接头处进行防水处理.

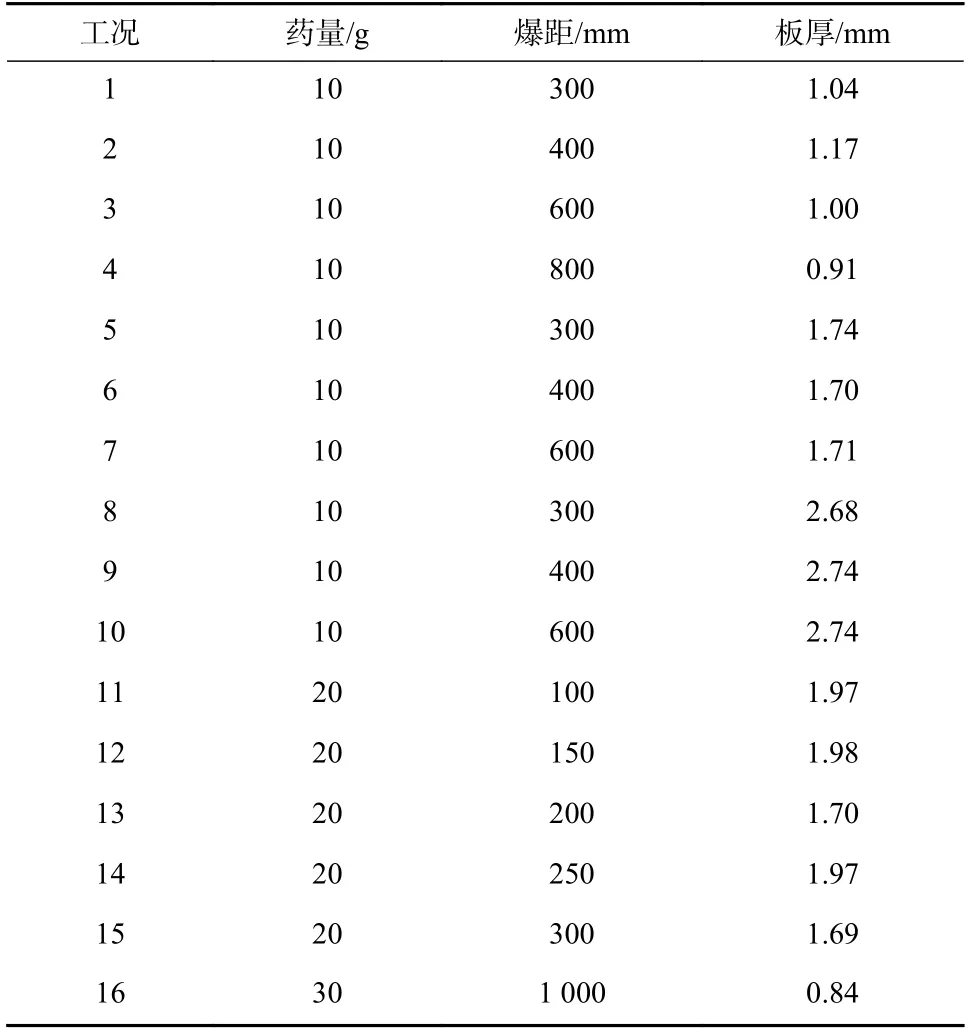
表1 实验工况表Tab. 1 Experimental scenarios table

1.2 靶板变形结果分析

实验后，靶板均出现“锅底形”塑性大变形，部分工况靶板变形情况如图2所示，图2中C-10-300-1.04表示实验工况为10 g TNT药量，300 mm爆距，1.04 mm板厚. 靶板中心点处的挠度测量值w0如表2所示.

表2 靶板变形挠曲面参数表Tab. 2 Parameter table of deformed bottom plate

图2 部分工况得到的靶板变形图Fig. 2 Deformed bottom plate obtained for some different scenarios

为了准确描述靶板的挠曲面形状，对靶板中轴线上不同位置处的挠度值进行测量，建立如图3所示的直角坐标系，并选取合适的函数对靶板的挠曲面进行拟合. 文献[13 - 14]使用式(1)、(2)和(3)表示靶板的挠曲面，然而，通过试验数据分析发现，对于靶板挠曲变形较小的工况4，式(1)～式(3)所表示的挠曲面与靶板的实际挠曲面吻合较好，而对于靶板挠曲变形较大的工况1，式(1)～式(3)所表示的挠曲面与靶板的实际挠曲面差异均较大，如图4所示. 因此，式(1)～式(3)均难以真实反映本文实验中靶板的挠曲变形情况.

图3 建立的直角坐标系Fig. 3 Cartesian coordinate system

图4 工况1和4按式(1)～(3)的拟合结果Fig. 4 Fitting results of scenario 1 and scenario 4 according to equations (1)to (3)

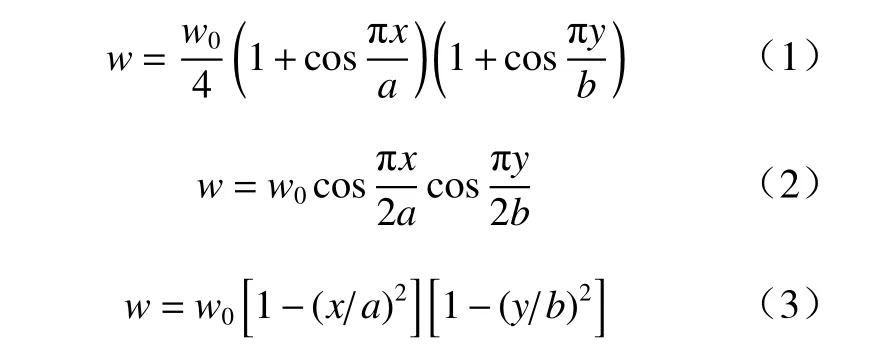
鉴于式(1)～式(3)只适用于靶板小挠度的情况，文本用试探法提出能同时满足小挠度和大挠度的式(4)，可以验证式(4)满足边界条件，即x=0或y=0时，w=w0，x=±a或y=±b时，w=0. 将靶板中轴线不同位置处的挠度值按式(4)进行最小二乘拟合，式中的w0为靶板中心点的挠度实测值，仅对指数n进行拟合，得到的拟合指数n和相关系数r的值如表2所示. 发现式(4)中的指数n与靶板中心点挠度w0符合负指数衰减规律，其关系大致满足式(5)，指数n随挠度w0的变化关系如图5所示.

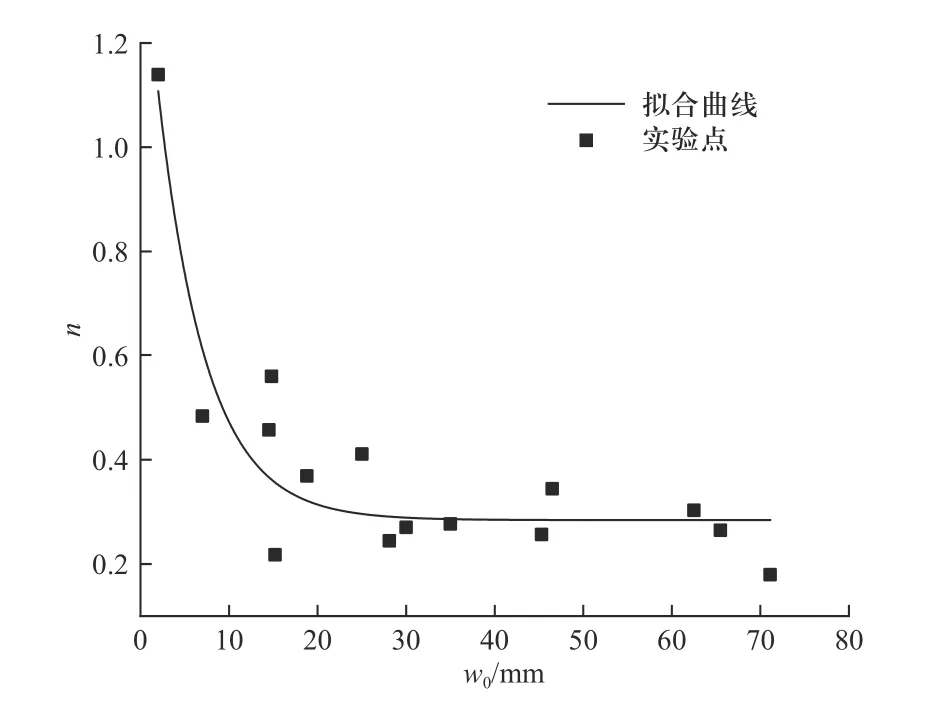
图5 拟合指数n随挠度w0的变化关系Fig. 5 Relationship between the fitting index n and the deflection w0

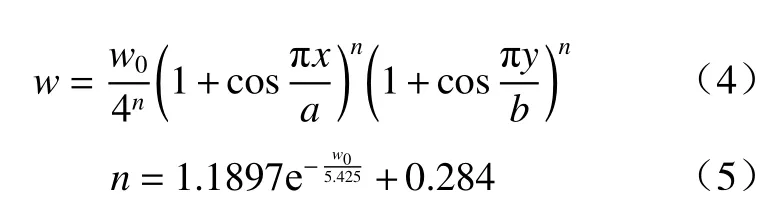
图6为使用式(4)对工况1～4的挠曲面拟合的结果，可以看出，式(4)的确可以拟合靶板的小挠度变形情况，对于靶板挠曲变形较大时的情况同样适用. 本小节拟合获得的靶板挠曲面为下文的理论分析提供依据.

图6 工况1～4按式(4)的拟合结果Fig. 6 Fitting results of scenario 1-4 according to equation (4)

1.3 壁面压力结果分析

为了获得靶板受到的冲击载荷，在靶板的迎爆面中心处布置一枚美国Dynasen公司的PVDF压力传感器，型号为PVF2-11-.25EK. 首先对购买的PVDF传感器进行焊接、水密处理，再使用双面胶将传感器粘贴在靶板中心位置处，然后连接电荷转换器，最后连接示波器进行读数. 示波器测量得到的为电压信号，需要将得到的电压值代入式(6)，计算传感器单位面积上产生的电荷量Q/A，单位μC/cm2，再代入式(7)计算得到冲击波压力p，单位MPa. 由于部分工况传感器损坏，仅有部分实验工况获得了有效的压力时程曲线数据，如图7所示.

式中：Cc为电荷积分器的电容，实测值为0.104 μF；us为示波器测量得到的电压信号，单位V；Ag为传感器的有效面积，取0.4 cm2；Cs为传感器的准静态校准系数，工况5为0.013 8，其余工况为0.014 2；af为电荷积分器和示波器之间的衰减系数，近似取1.

对图7所示的压力时间曲线按指数衰减规律进行拟合[15]，得到壁面压力峰值p′m和时间常数ψ，结果如表3所示.

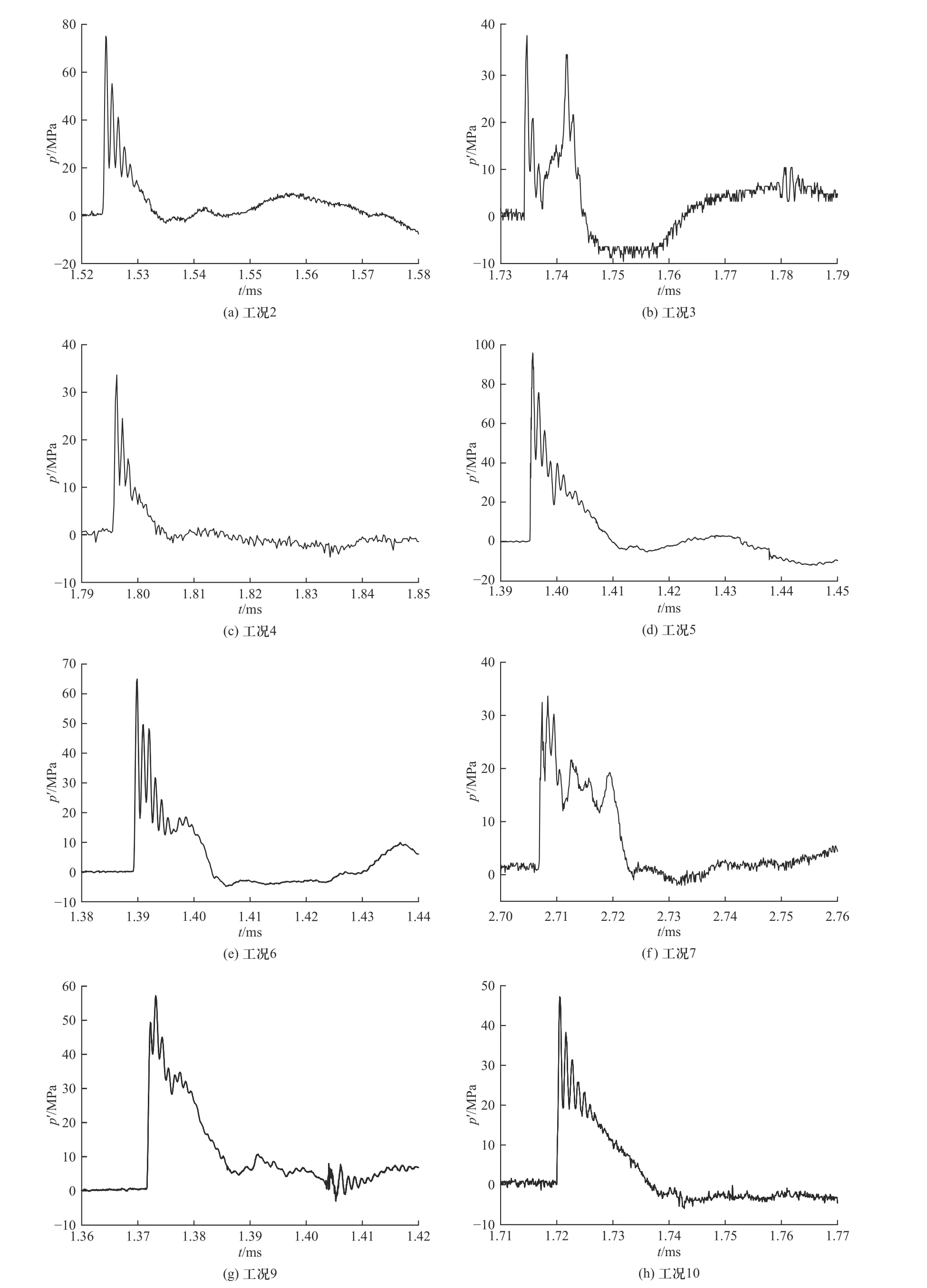
图7 PVDF传感器测得的压力时程曲线Fig. 7 Pressure time history curve measured by PVDF sensor

表3中自由场压力峰值和时间常数按式(8)～(10)确定[16]，从表3中的数据可以得出，壁面压力峰值较自由场压力峰值大，平均为2.48倍，壁面压力时间常数较自由场小，平均为0.216倍. 部分实验工况未获得壁面压力数据，由于目前尚没有学术界公认的计算壁面压力峰值及时间常数的经验公式，因此本实验其他工况的壁面压力峰值p′m取相同工况下自由场压力峰值pm的2.48倍，时间常数ψ取相同工况下自由场时间常数θ的0.216倍，为下文的理论分析提供数据支撑.

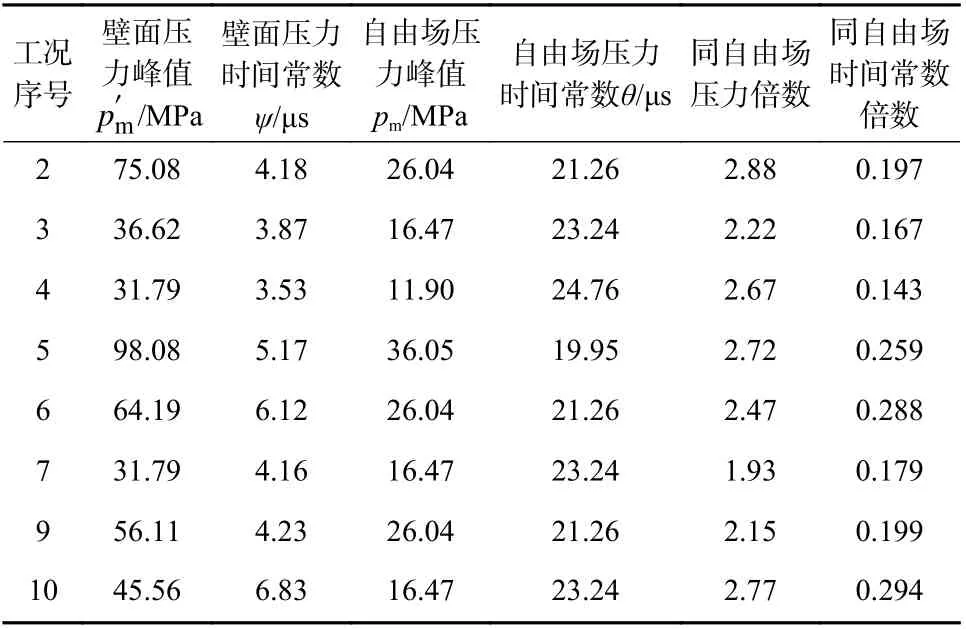
表3 PVDF传感器压力测试结果Tab. 3 PVDF sensor pressure test results

式中：pm为自由场冲击波压力峰值；θ为自由场冲击波时间常数；W为TNT当量；R为爆距；R0为药包半径.

2 理论分析

此部分从理论上计算作用到靶板上的能量(包括冲击波能Es和气泡能Eb)和浮体模型获得的能量(包括浮体动能Ek和底部靶板塑性变形能Ep)，并定义浮体模型的能量利用率α，对结果进行详细分析.

2.1 冲击波能和气泡能分析

本小节考虑近距离爆炸球面波效应，得到了模型获得的冲击波能量. 水下爆炸自由场冲击波超压pm、时间常数θ按式(8)～(10)计算，将水下爆炸冲击波能分成冲击波波头能量和滞后流能量，二者的能流密度Ew1和Ew2分别按式(11)和式(12)计算[16].

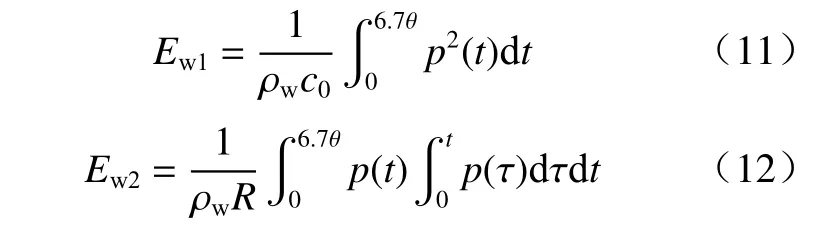
式中：Ew1为冲击波波头能流密度；Ew2为滞后流能流密度；ρw为水的密度；c0为水中声速.

将式(8)～(10)分别代入式(11)和式(12)，可以得出计算冲击波波头能流密度和滞后流能流密度为

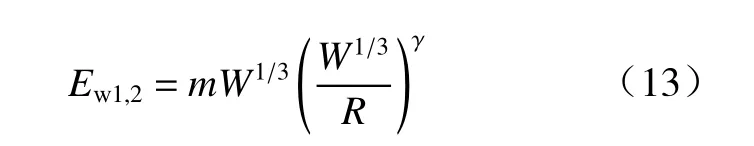
式中常数m和γ的取值如表4所示.

表4 冲击波能流密度参数取值表Tab. 4 Table of shock wave energy flow density parametervalue

对于球面冲击波而言，作用在靶板表面每一处的能流密度与距离爆心的位置有关，不能用一个不变的量来表示. 基于该问题，做出球面波与1/4靶板的作用关系示意图如图8所示，靶板上任意一点到爆源的直线距离为

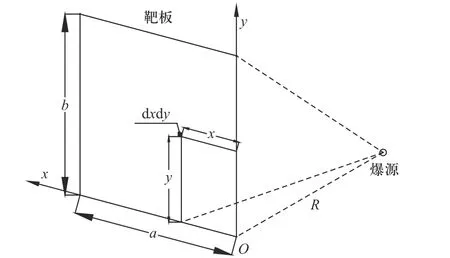
图8 靶板与球面冲击波作用关系图Fig. 8 Diagram of interaction between plate and spherical shock wave

用R′替换式(13)中的R，可得修正后的能流密度为

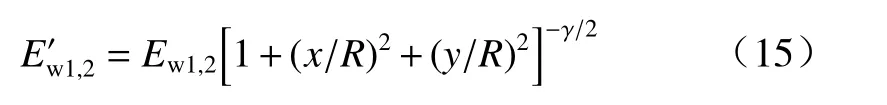
由式(15)可以看出，作用到靶板上的能流密度是一个变量，对整个靶板区域进行积分，可以得到作用到靶板上的冲击波波头能量Es1和滞后流能量Es2，

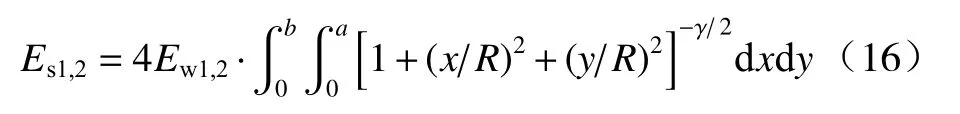
式中：a、b分别为靶板的半长和半宽.

作用到靶板上的爆炸冲击波的能量Es表示为波头能量Es1与滞后流能量Es2之和，即Es=Es1+Es2.

作用到靶板上的气泡能可以近似表示为

式中：EbTNT为TNT的气泡能，约占TNT水下爆炸总能量的47%，取2 MJ/kg[16].

2.2 模型动能分析

考虑浮体模型运动时浮力的变化，用PVDF传感器测量得到的壁面压力时程作为浮体模型的爆炸输入载荷，对浮体模型进行受力分析，计算浮体模型的最大动能Ek.

实验工况1～10未加底部法兰板，模型总质量m=42.47 kg，模型底部面积A1=0.16 m2；其余工况加了底部法兰板，模型总质量m=67.42 kg，模型底部面积A1=0.25 m2. 另外，模型在水平面处的横截面积A2=0.102 4 m2，重力加速度g=9.8 m/s2，吃水深度H=0.2 m，水的密度为ρw=1 000 kg/m3，模型的刚体运行速度为v，刚体位移为s.

壁面冲击波压力为

水面浮体受到重力mg、浮力F、冲击波压力p'A1的作用，由牛顿第二定律可得

其中浮力为

代入式(19)可得

式(21)为2阶常系数非齐次线性微分方程，初始条件：当t=0时，位移s=0且速度ds/dt=0，解得位移S和 速度v的表达式分别如式(22)和(23)所示.

2.3 塑性变形能分析

考虑靶板弯曲应变和膜力拉伸应变的耦合作用，使用前文拟合得到的挠曲面函数，计算靶板的塑性变形能Ep.

根据直法线假设，薄板结构在受到爆炸冲击载荷时产生两部分应变，一部分为板结构的中面拉伸应变，此部分变形沿z方向不发生变化. 另一部分与z成正比，为弯曲应力作用下的弯曲应变. 忽略靶板在x和y方向上的位移[7]，可得靶板任意点的应变为

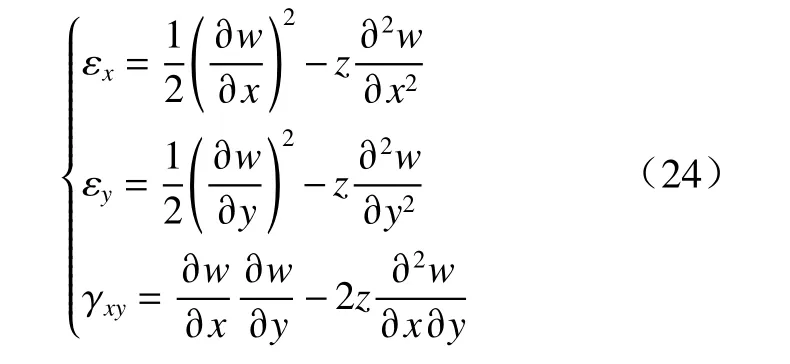
式中：w为靶板任意点处在z方向的挠度，将靶板挠曲面函数式(4)代入式(24)可得，

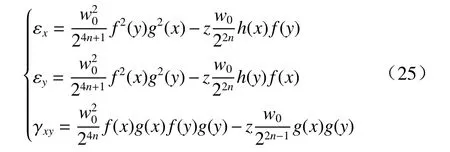
其中，

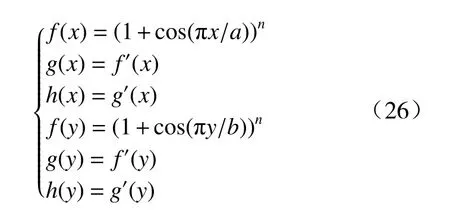
式(25)体现了弯曲应变和膜力拉伸应变的耦合作用，分别令εx=0、εy=0可以得到两个中性面的表达式(27)，图9所示为工况1靶板中性面Zx(x,y)的形状.在中性面Zx(x,y)位置处，εx=0；在中性面上方，εx>0，靶板在x方向处于拉伸状态；在中性面下方，εx<0，靶板在x方向处于压缩状态. 在中性面Zy(x,y)位置处，εy=0；在中性面上方，εy>0，靶板在y方向处于拉伸状态；在中性面下方，εy<0，靶板在y方向处于压缩状态.

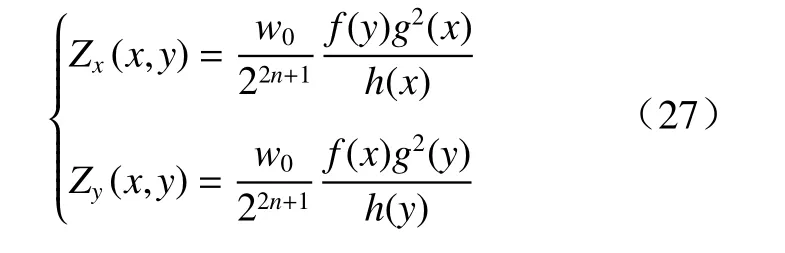
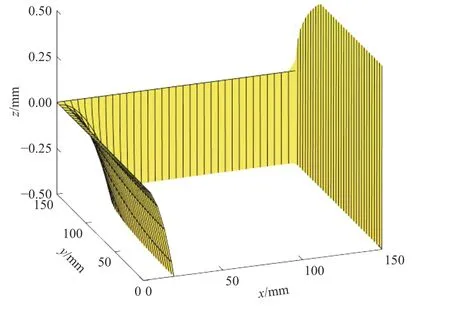
图9 中性面Zx(x,y)的曲面形状Fig. 9 Neutral plane Zx(x,y)

靶板的塑性变形能Ep由式(28)计算，式中σs为靶板的屈服极限，对于靶板的拉伸和压缩区域，需要分别积分[14]，为了确定积分区域，首先求出中性面Zx(x,y)和Zy(x,y)与靶板的交线y(x)和x(y)，即表达式(29)，图10所示为交线y(x)的形状，然后求出y(x)与x轴的交点坐标(x0，0)、x(y)与y轴的交点坐标(y0，0).

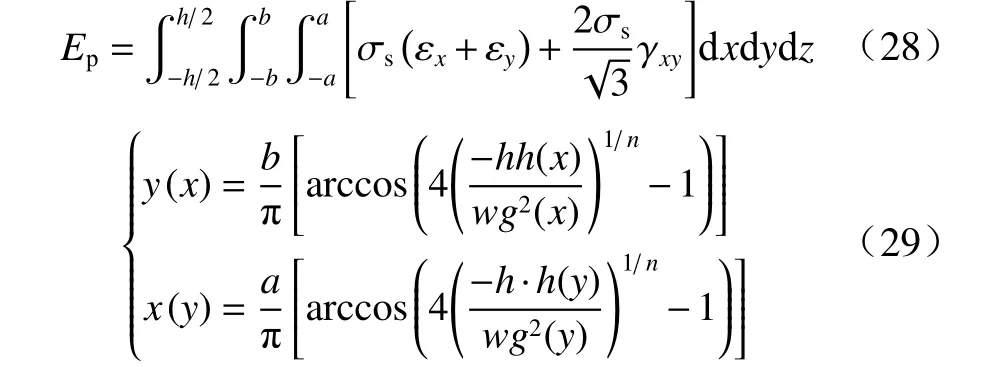
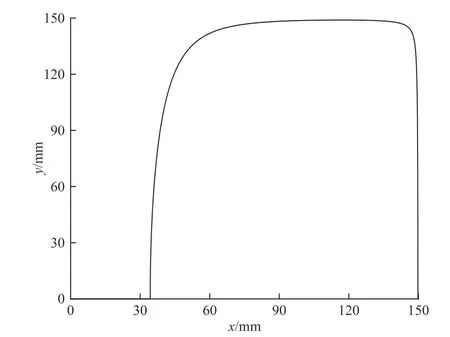
图10 中性面Zx(x,y)与靶板的交线y(x)Fig. 10 Neutral plane Zx(x,y) and the target intersecting line y (x)

确定积分区域后，便可以得到塑性变形能Ep为

将式(25)～(27)和(29)代入式(30)，使用MATLAB编程即可对不同工况下靶板的塑性变形能Ep进行求解.

2.4 模型能量利用率分析

为表示浮体模型所受到的爆炸冲击环境，使用文献[17]中定义的量纲一的数Φ，

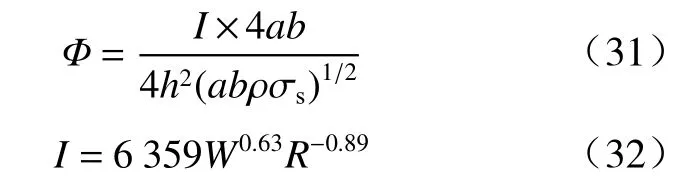
式中：ρ为靶板的密度；σs为靶板的屈服极限.

计算各个工况下的量纲一的数Φ、冲击波能Es、气泡能Eb、塑性变形能Ep、动能Ek，并按式(33)计算模型的能量利用率α，结果见表5.

表5 浮体模型能量分析表Tab. 5 Floating model energy analysis table

浮体模型能量利用率α随Φ的变化关系如图11所示.

图11 模型能量利用率α随Φ的变化关系图Fig. 11 The relationship between energy utilization rate α and Φ

近似满足二次函数关系，

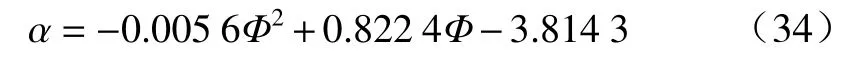
具体表现为：α随Φ的增加先增加后减小，炸药水下爆炸作用到浮体模型上的冲击波能和气泡能并没有被完全利用，当Φ在50～90时，浮体模型对水下爆炸能量的利用率α达到最高，达到20%～30%.

水下爆炸冲击波在到达靶板表面时，会发生复杂的反射、透射和界面空化现象，仅有部分冲击波能可以被有效利用. 当爆距较小时(对应于本研究为Φ值较大时)，冲击波压力峰值较高，一方面导致冲击波产生较强烈的反射作用[18]，另一方面导致浮体模型产生较大的速度，流固耦合界面处发生空化现象，冲击波载荷被截断，两种现象都使冲击波的能量利用率降低；当爆距较大时(对应于本研究为Φ值较小时)，冲击波反射作用和界面空化现象减弱，冲击波的能量利用率提高；但是，当爆距过大时(对应于本研究为Φ值过小时)，冲击波强度减弱，能够对靶板造成毁伤的冲击波脉宽变短，部分冲击波能为无效能量，不能够对靶板造成有效毁伤.

水下爆炸气泡内部为高温高压的爆轰产物，因此，气泡能主要以内能和压力势能的形式存在. 当爆距较小时(对应于本研究为Φ值较大时)，气泡射流难以形成，气泡内部的内能和压力势能无法对靶板造成局部毁伤，部分内能以热量的形式在流场中耗散，气泡能的利用率较低；当爆距较大(对应于本研究为Φ值较小时)，恰好达到气泡射流形成条件时，气泡能的毁伤威力得以充分发挥，此时气泡能的利用率达到最大；但是，当爆距过大时(对应于本研究为Φ值过小时)，气泡能主要转化为周围流场亚声速流动的动能，即滞后流，主要对大型舰船结构造成整体毁伤，对于本研究所采用的小型浮体模型而言，滞后流的能量难以充分利用.

3 结 论

本文对水面浮体模型在水下爆炸载荷下的变形机理进行了实验和理论研究，得出以下结论：

①模型底部靶板在水下爆炸载荷下的挠曲面可以用式(4)的形式表示，式(4)中的指数n随着靶板中心挠度值w0的增加呈现式(5)所示的负指数衰减规律. 本文理论研究得到的式(4)对靶板大变形和小变形的情况都能很好地拟合，较传统的拟合公式(1)～(3)具有更强的适用性.

②模型底部靶板壁面上冲击波压力峰值较自由场压力峰值大，约为自由场压力峰值的2.48倍，壁面冲击波时间常数较自由场时间常数小，约为自由场时间常数的0.216倍. 相对于自由场冲击波压力载荷，本文试验研究测得的壁面冲击波压力载荷更能真实反映靶板的水下爆炸冲击环境，可为水下爆炸载荷下平板结构动态响应的分析计算提供参考.

③模型整体能量利用率α随量纲一的数Φ的增加先增加后减小，当Φ在50～90之间时，浮体模型对水下爆炸能量的利用率α达到最高，达到20%～30%.

④由于实际工况中的水面舰船底板结构并非完全固支，而是会在水下爆炸载荷作用下出现垂向位移，因此，本研究基于水面浮体模型得到的结论更为准确地反映了实船在水下爆炸载荷下的响应特征，可为水下武器的高效毁伤技术提供参考.