关注数学阅读，培养解题能力

林培钦

在教学中，很多教师忽略了数学阅读的重要性，没有引导学生对数学文本进行有效解读，致使学生解题能力不强、错误率较高。学生的解题常常是基于课本例题的掌握情况，稍作变式尚能模仿解答，一旦加以拓展或综合训练就手足无措。所以，数学教学要立足数学文本，引导学生理解数学语言，激活学生的数学思维，从而实现高效解题。

一、把握核心信息，提高解题实效

核心问题是整堂课的关键，教师的教学围绕核心问题进而设计系列的问题串，学生把握好核心问题，就能顺利解答由它衍生的其他问题。同理，在学生阅读数学文本时，教师要引导他们学会抓住文本中的核心词。抓住核心词就是扼住解题的关键，能有效地厘清解题脉络，分析题干相互间的关系，从而实现有效答题。

例如，解答这样一道题：有一根木料，用1/10小时可以截成5段，如果每截一段的时间相同，那么要截成8段，一共需要（  ）小时。不少学生没有深入分析题目，出现“1/10÷5×8”或“1/10÷（5-1）×8”这两种类型的错误。究其原因，第一种错误是根本没有考虑“截5段只要截4次”的道理，要用植树问题的模型来解答此类问题;而第二种解法能用植树问题的模型来思考问题，也明白了“截5段其实只要截4次”，但考虑问题不周到，忽略了后续的截8段只要7次的时间之和。像此类题型，我们要引导学生认真审题，通过画图帮助理解，抓住关键的信息“每截一段的时间相同”，做到“眼到、手到、心到”，才能正确列出算式：1/10÷（5-1）×（8-1）。

因此，教师在引导学生阅读数学文本时，需要注意引导学生全面感知文本内容，紧扣核心信息，如“和、差、倍、分、一共、剩下、减少、提前、平均”等，可以通过加重音读题、做标记等方式来帮助分析题目中隐含的数量关系，激活学生思维，提高解题实效。

二、借助经验阅读，增强解题趣味

小学生的思维方式以形象思维为主，抽象的数学知识，特别是一些深奥的数学语言，经常让学生觉得很陌生;再加上枯燥的计算和烦琐的推理，学生很容易失去学习数学的兴趣。教师在引导学生阅读数学文本时，可以引导学生将生活经验与数学知识进行关联思考，这有利于加深对数学语言的理解，提升解题效率。

例如，在“周长”的教学中，笔者在课初让学生观察“蚂蚁跑圈”，让学生直观明白“从同一个地方出发，又回到同一个地方”，即首尾相连就是“一周”;接着让学生动手实践，测量各种平面图形的周长，思考怎样测量硬币的周长。笔者在巡视时发现学生能借助绕操场跑步的生活经验展开分工合作，或用绳测法，即用绳子缠绕硬币一周，再把绳子拉直测量;或用滚测法，即在硬币上做个标记，在直尺上滚动一周，观察一周滚过的长度。两种方法，都利用了“化曲为直”的方法测量出硬币一周的长度。学生懂得借助生活经验展开思考，在充分的实践体验基础上，避免了思维盲目性，形象且深刻地理解了周长的内涵。最后，笔者让学生尝试解答如下题目：用4根小棒围成一个长方形并拉动（如图1所示） ，周长变了吗？为什么？学生有了前面充分的体验后，明白比较周长就是在比较小棒的长度，各根小棒的长度没有改变，周长也不会变，即周长和形状无关。这种引导学生借助生活经验来阅读数学文本，既激发学生学习数学的兴趣，也提升学生的数学阅读能力和数学解题能力。

三、注重比较阅读，明晰解题条理

在解决一些题目条件有关联的数学问题时，学生很容易产生混淆，不能很好地分析数量关系。这时候，教师可以有意识地引导学生对文本展开比较阅读，厘清不同题型之间的差别，辨别各种量之间的数量关系，能促进他们对文本的理解更到位，提高解题能力。

如在教学“分数”的内容时，笔者出示如下题组：（1）苹果有60个，桃子的个数是苹果的1/4，桃子有多少个？（2）苹果有60个，是桃子个数的1/4，桃子有多少个？（3）苹果有60个，桃子的个数比苹果的1/4还多20个，桃子有几个？（4）苹果有60个，比桃子个数的1/4还多20个，桃子有多少个？这一题组所要解决的问题是一样的，但条件却完全不同。笔者让学生对题组进行比较阅读，比较出这四道题的不同之处。学生小组合作，在对题组的“同”与“不同”的辨析中明白：问题相同的情况下，条件不同，其题意、解法也完全不同。这类题目的解题关键是要确定标准量，才能列出对应的等量关系式。学生列出如下关系式：（1）苹果的个数×1/4=桃子的个数;（2）桃子的个数×1/4=苹果的个数;（3）苹果的个数×1/4+20=桃子的个数;（4）桃子的个数×1/4+20=苹果的个数。这种在教学中开展的比较阅读，让学生在阅读中学会分清不同条件，学会找到题目中的“单位1”和数量关系，从而正确解题。

四、落实阅读交流，促进深度学习

与他人交流，倾听他人对同一事物产生的不同思维方式和解决问题的不同策略，及时反思与完善自己的不足，能形成更全面的数学认知结构。因此，教师在引导学生进行数学阅读时，应有意识安排交流环节，让学生们各抒己见，集思广益，或许会有意外的收获。

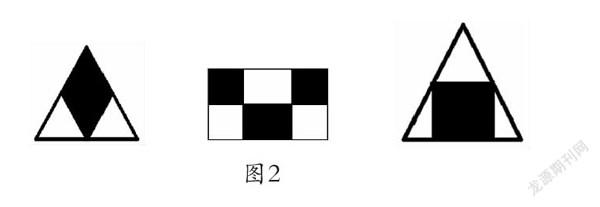
如在“图形的转化”的教学中，笔者出示下面一道题：下图中的阴影部分是否可以用1/2表示？为什么？

对于图形二，大部分学生能作出直观的判断。但对于图形一和图形三，一些学生不敢作出肯定判断。此时，笔者让学生再次阅读题目，同时让一些空间观念较强的学生在班內向其他学生说出自己的想法，组织学生进行交流和讨论。不一会儿，有学生发现题目要验证的阴影部分是否是图形的1/2，即一半，那么可以用“平均分”的方法对图形进行平分，将阴影部分剪切下来，然后和空白部分重叠，看大小是否一样;也有学生提出既然是一半，那么不用剪切，而可以用“轴对称”的方法对图形进行折叠，看阴影部分和空白部分是否大小相等。最后，学生在交流中发现图形二也可以用同样的方法进行验证，明确要看一个图形阴影部分是否占整个图形的一半，用轴对称的方法进行验证最简单。

通过再次阅读与交流讨论，不但丰富了学生对文本的解读，而且逐步培养了他们推理的习惯。教师要善于把握住交流的契机，发挥引导作用，让学生在交流中进行思维的碰撞，以实现对数学题目的正确解读。

（作者单位：福建省安溪县金谷中心学校 责任编辑：王振辉）

2918500511308