基于响应面优化的导弹尾翼轻量化设计

杨 辉，王 琦，何国毅，张霄昕，陈龙胜

(南昌航空大学飞行器工程学院，南昌 330063)

0 引言

降低结构重量一直是飞行器设计的重要目标，更轻的结构重量可使飞行器获得更好的航程和机动性。随着飞行器的飞行速度越来越大，受到气动载荷也越来越大，这使飞行器结构的强度、刚度要求和重量要求之间的矛盾更加尖锐。

飞行器舵翼的主要作用是控制飞行姿态，工作时承受较大的载荷，设计时需要综合考虑。对此，国内外学者进行了大量的研究。李士静[1]对某型导弹铸造弹翼在多单元、多种约束、单工况的条件下上下壁板的最小重量设计进行了探讨，并取得不错的效果；张刚等[2]采用拓扑优化方法对整体式弹翼的骨架结构进行了优化迭代，实现了轻量化设计；温晶晶等[3]对整体式弹翼骨架结构进行拓扑优化，并采用节点载荷等效法构建弹翼骨架的典型受力环境，解决了弹翼待设计区域的单元既参与受力又可能因为优化而被删减的设计矛盾，达到了较好的轻量化效果；吴元琦[4]从甲虫鞘翅断面微结构中提取设计元素,设计出一种仿生轻质夹芯结构并用于舵翼结构，实现了轻量化设计；周子童[5]针对飞行器中的薄壁结构提出了一种薄壁结构的高刚度多级加筋设计方法，通过布置主级稀疏加筋和次级密布点阵,对薄壁结构刚度进行层级增强,在提升结构面内和面外刚度的同时,实现结构的轻量化设计；Li等[6]提出了一种同时优化加劲肋布置和截面拓扑的新型拓扑优化方法并通过算例证明了方法的有效性；林纯景[7]对飞机机翼肋板结构布局问题采用了拓扑、尺寸和形状三级优化的方法完成肋板轻量化设计。

上述学者的研究对象多为尺寸较大的空心舵翼，对于尺寸较小的实心舵翼，由于其翼面厚度较小，少有学者进行结构优化研究，而随着3D打印技术在航空制造方面的运用，传统设计产品的思想将随之改变，中空加支撑结构的研究也有了较大的现实意义[8]。文中以某常规导弹实心尾翼为研究对象，基于有限元分析和响应面优化方法，研究其轻量化问题。

1 尾翼建模及受载分析

1.1 实心尾翼建模

建立简化几何模型，为真实反映尾翼的受力特性,将翼面与弹身的连接支耳也包含在有限元模型中，尾翼实体模型以及部分几何参数如图1所示。

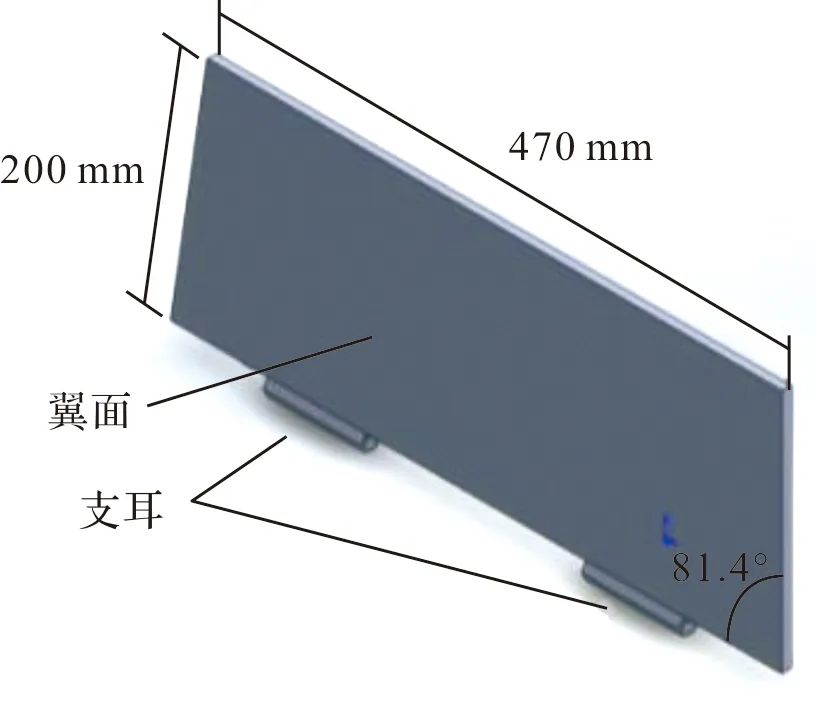
图1 尾翼实体模型

1.2 受载分析

图2为导弹舵翼的分布情况。由于不同弹翼的工况有所不同，因此需对尾翼工作状态下的受载情况进行分析。

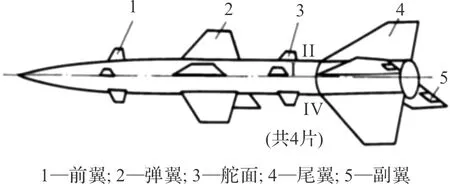
图2 导弹舵翼分布

导弹尾翼在飞行过程中主要受到气动力和重力的作用，重力对尾翼应力、变形的作用效果相对于空气动力来说影响很小，故不计入考虑，而空气动力主要考虑翼面法向力Ry作用带来的载荷效果，其计算公式为[9]：

(1)

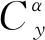
忽略翼面边界对气动特性的影响，翼面所受的载荷g可视为均布载荷,其大小可表示为[9]：

(2)

q的方向为沿尾翼厚度方向且垂直于翼面。

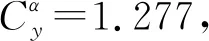
2 实心尾翼有限元分析

首先设置材料参数，该导弹尾翼采用的材料是高强度调质结构钢，具有高的强度和韧性，表1为材料的主要参数。经过网格无关性验证并参照相关文献，在兼顾计算精度和工作效率的情况下，选用4面体单元，设置单元尺寸为1 mm[10-11]。 对翼面施加0.107 MPa均布载荷，对支耳轴孔施加全固定约束。求解得到：最大变形为4.614 mm，最大应力为1 014.3 MPa。图3、图4为实心尾翼应力和变形云图。

在最近由上海市商务委员会和上海市外商投资协会联合召开的“辉煌外资四十年 风雨同舟再出发”——上海市外资企业表彰、双优百强发布会上，上海卡博特公司作为在上海深耕30年以上的外资企业代表获得了“基业长青”荣誉证书。这是上海市政府为表彰外商投资企业对上海经济、社会发展的突出贡献，集中展现改革开放40年来上海利用外资领域取得的成就，并对有突出贡献的企业和个人予以表彰。

表1 材料主要参数

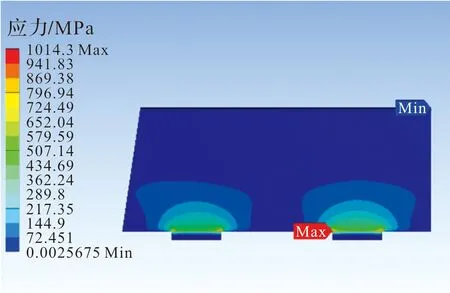
图3 实心尾翼应力云图

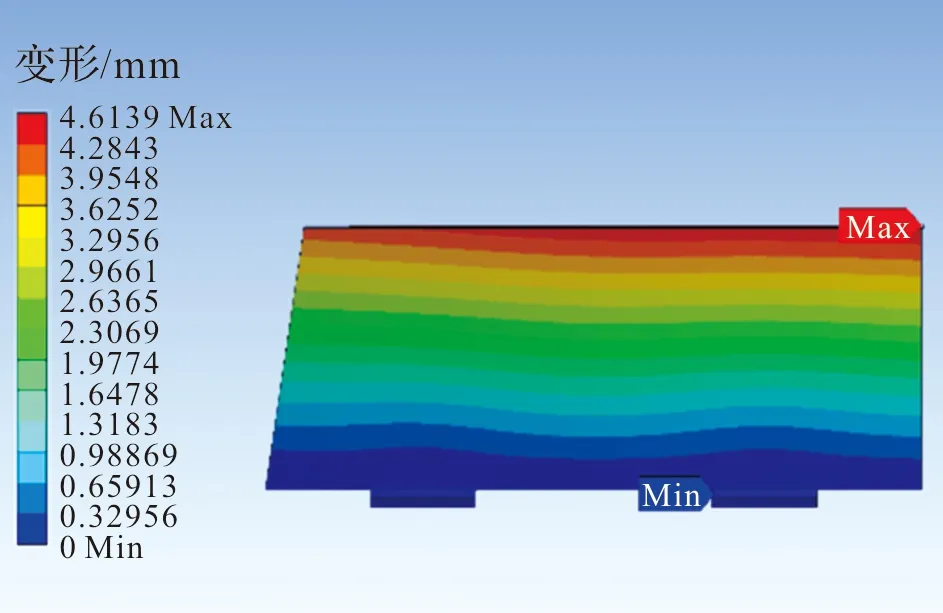
图4 实心尾翼变形云图

由应力分析和图3、图4可知，靠近支耳处翼面应力较大，远离支耳处翼面位移较大，符合实际情况；同时，远离支耳约40 mm处应力降低至200 MPa左右，远小于许用应力，设计存在较大的冗余。

3 冗余材料的去除与有限元分析

3.1 冗余材料的去除(中空化)

尾翼外廓需要维持特定的气动外形,不能轻易改动。由静力学分析可知：靠近支耳的区域翼面应力较大，此区域不宜去除；尾翼面上下表面部分需要保留一定的厚度以起蒙皮的作用，不能过薄，因此将这些区域定为非设计区域。外廓内部区域布满材料,可对其进行去除以设计出合理的支撑结构,因此定为设计区域[3]。去除中空设计区域的冗余材料，得到如图5所示的空心尾翼。

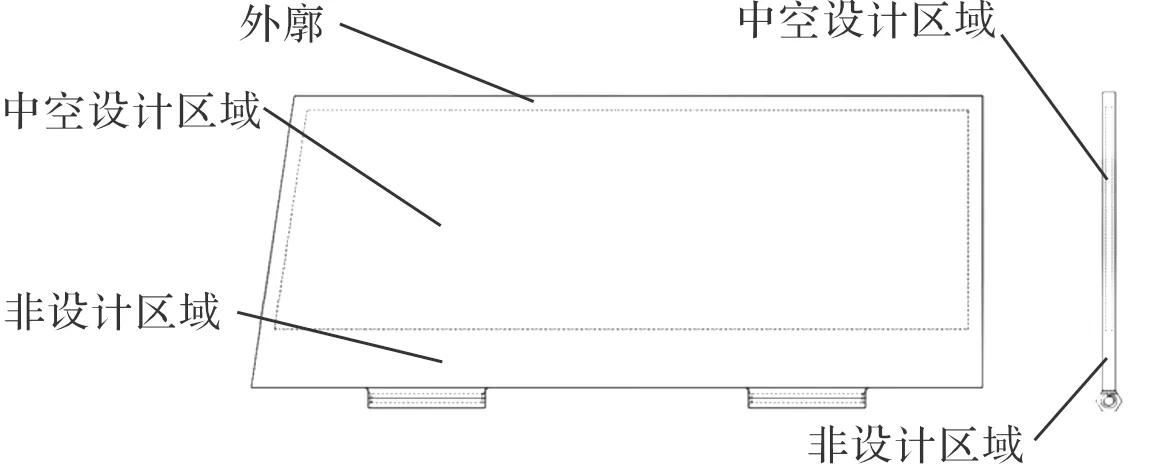
图5 空心尾翼设计方案

3.2 空心尾翼有限元分析

对空心尾翼进行静力学分析，结果如图6、图7，发现翼面较多部位应力增大，支耳处的最大应力增加至1 629.8 MPa，超出该材料的许用应力；翼面变形较实心尾翼变化也较大，最大变形达11.3 mm。中空后的空心尾翼无法完成原工况下的任务，需要对结构补强。

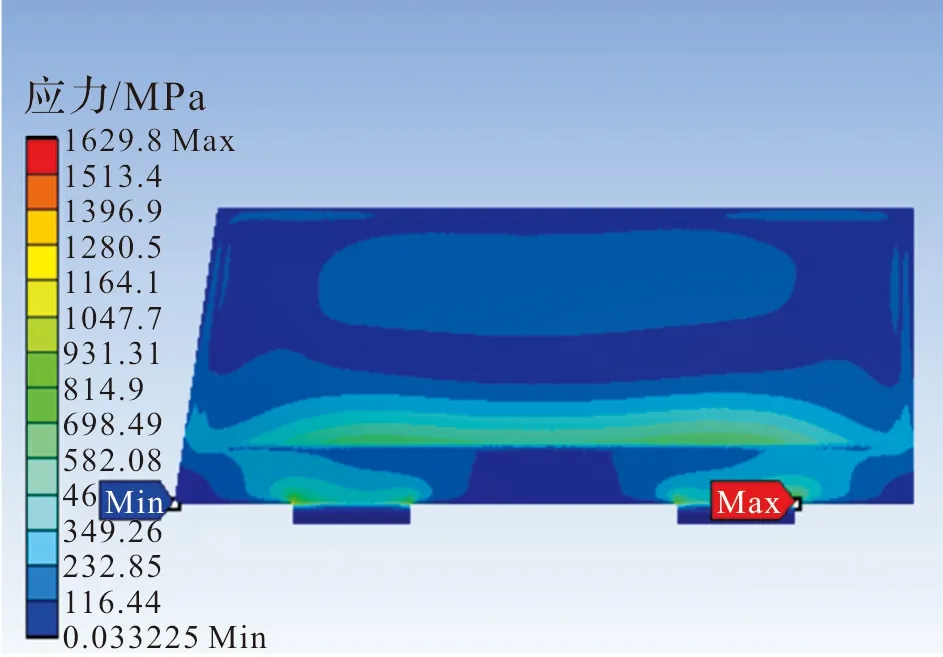
图6 空心尾翼应力云图

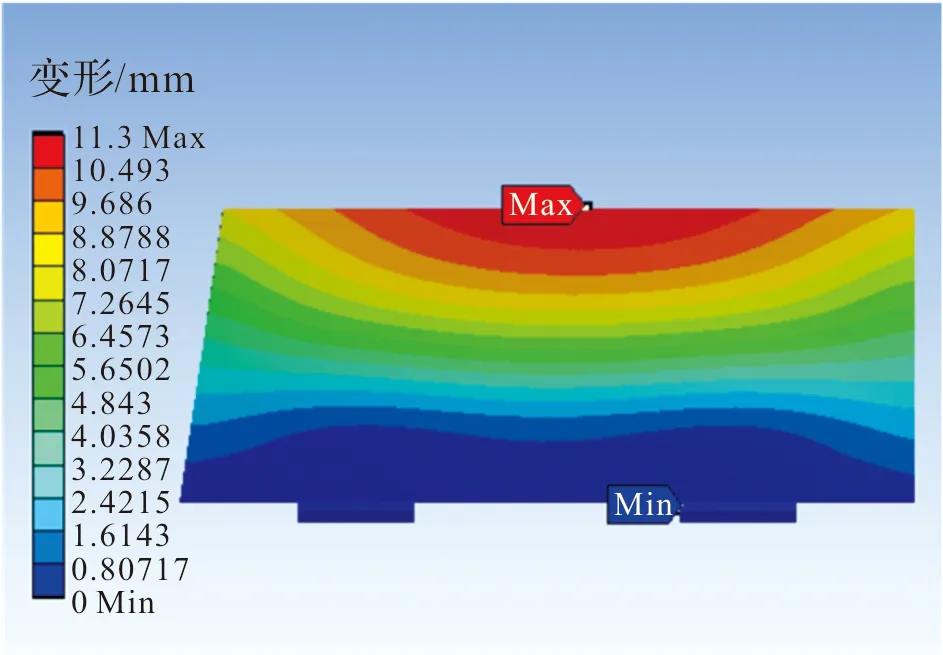
图7 空心尾翼变形云图

4 补强及优化

4.1 补强方案

参照飞机翼梁、肋结构，以及大型导弹舵翼的设计方法对尾翼进行补强。梁、肋、桁条等加强结构一般采用规律的平行、十字、井字等铺设方式[12-13]。文中对加强筋数量进行了初步试验，结果表明：同样的肋条宽度下，在展弦两个方向上，随着均匀布置的加强筋数量的增多，重量直线上升，最大应力、最大变形逐渐减小。综合考虑重量、变形、应力以及其变化趋势，确定了展向7根和弦向1根的方案，布置方案如图8所示。

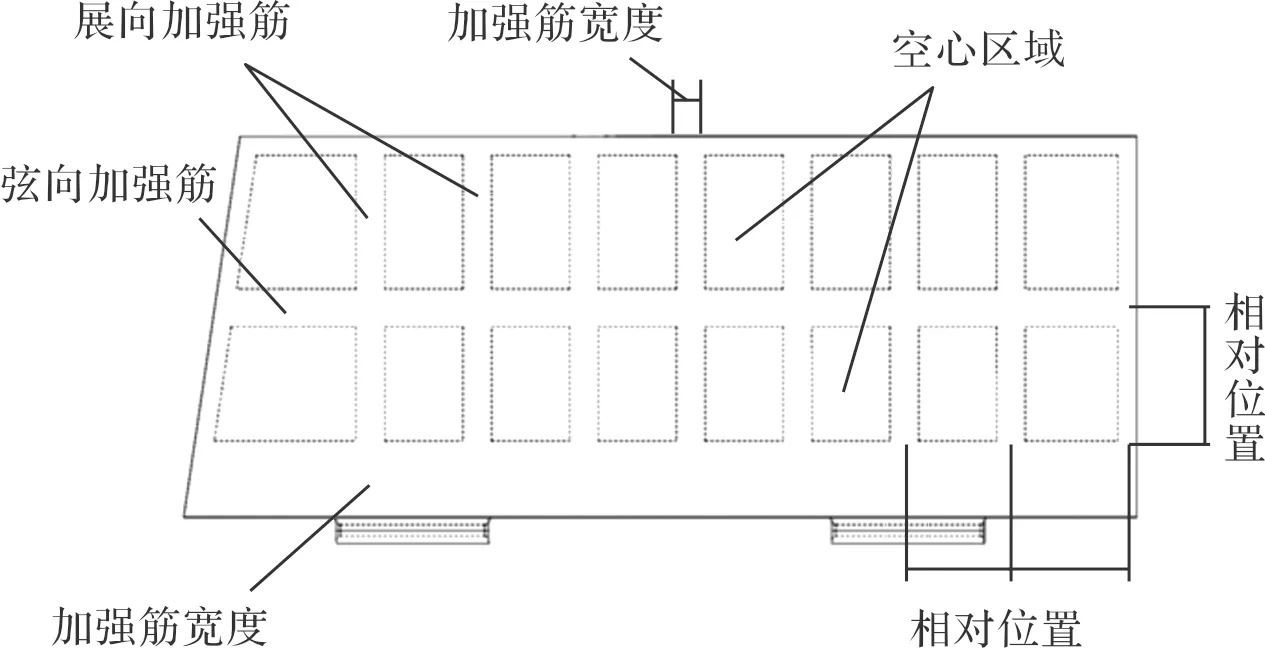
图8 均布加强筋布置方案

加强筋的宽度以及加强筋的相对位置对尾翼强度、刚度和重量均会产生影响，下面用响应面优化方法进一步优化加强筋的位置和宽度参数。

4.2 建立响应面优化数学模型

根据实际情况，将原结构最大应力作为约束，将最大变形和最小重量作为目标函数，建立以下数学模型：

(3)

式中:Pi为设计参数；D为最大变形量；M为尾翼质量；σb为尾翼的最大应力；ai,bi分别为第i个设计变量的上下限。

表2 参数取值范围 单位：mm

4.3 参数敏感性分析

响应面优化的效率与参数的个数有关，故在优化之前需要分析各个参数对目标的影响效果大小，剔除影响效果小的参数以减少参数个数，提高优化过程中的计算效率。

文中采用Spearman′s Rank相关性分析方法，该方法被认为是更精确的方法[14]。经分析，得到各个参数对目标的敏感性，图9所示为敏感性分析柱状图。

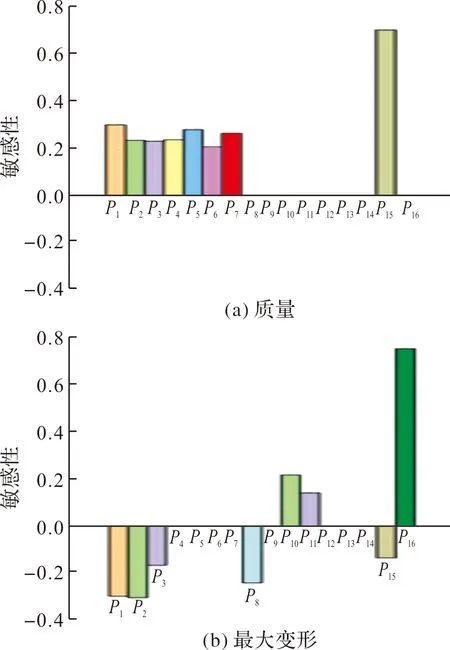
图9 参数敏感性分析柱状图

可见：参数P1，P2，P3，P8，P10，P11，P15，P16对最大变形影响较大，且P10，P11，P16呈正相关，其余为负相关；P2，P5，P6，P7，P8，P11，P13，P14，P16对最大应力影响较大，其中P6，P7，P11，P13，P14，P16为正相关，其余为负相关；在后续的试验中选取上述14个相关性强的参数参与寻优运算，以提高计算效率。

4.4 DOE抽样

拟合响应面需要进行试验设计(design of experiment，DOE)抽样，样本点选取位置的好坏，会影响DOE计算成本和响应面的精度。现阶段，常用取点方法的共同之处是尽量用最有效的和最少量的样本点对设计空间进行填充，且试验样本点的位置满足一定的对称性和均匀性要求[14]。文中采用中心复合设计(central composite design，CCD)方法,根据前面分析，选取14个参数参与拟合响应面，生成281个样本。采用标准二次多项式的方法拟合响应面[16]，图10～图13为部分输入变量与输出变量的响应图。

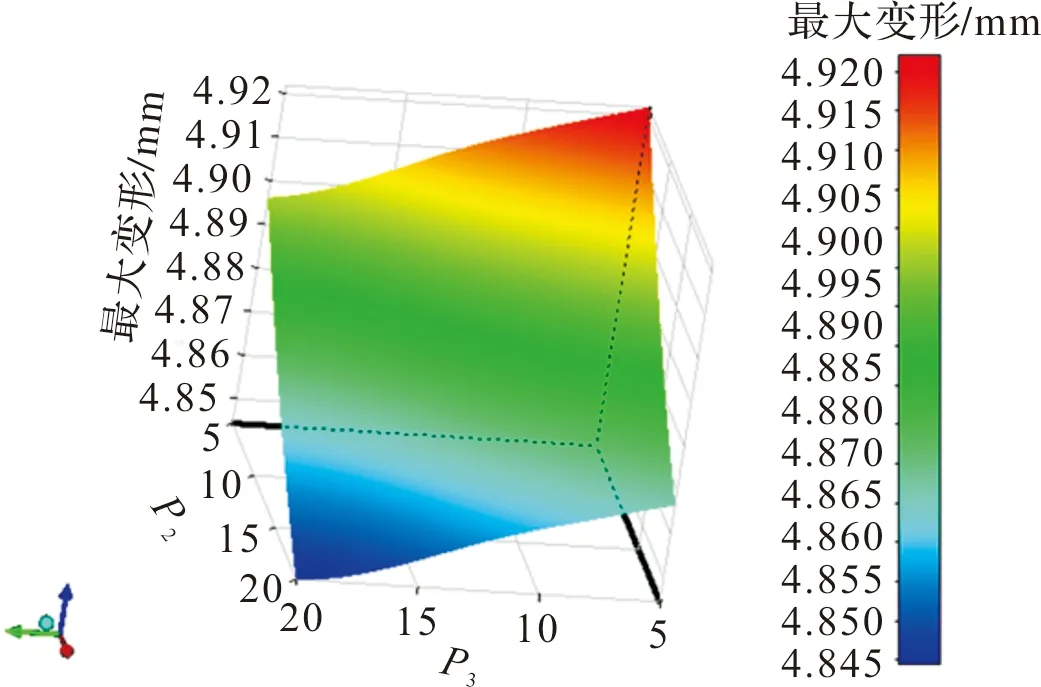
图10 参数P2，P3与最大变形的响应图

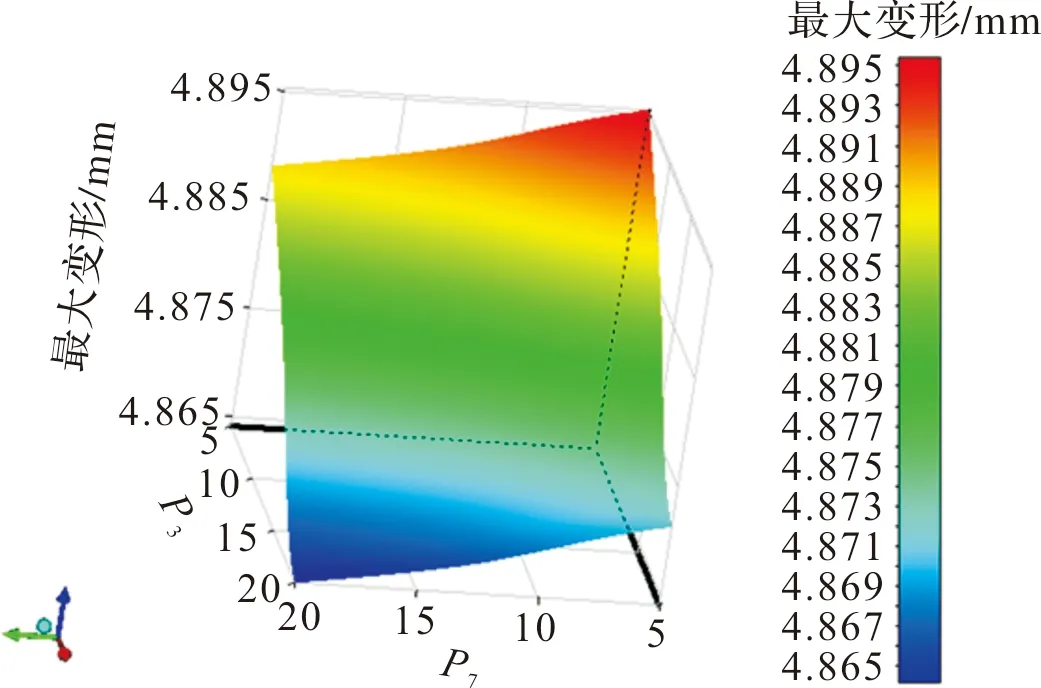
图11 参数P3，P7与最大变形的响应图

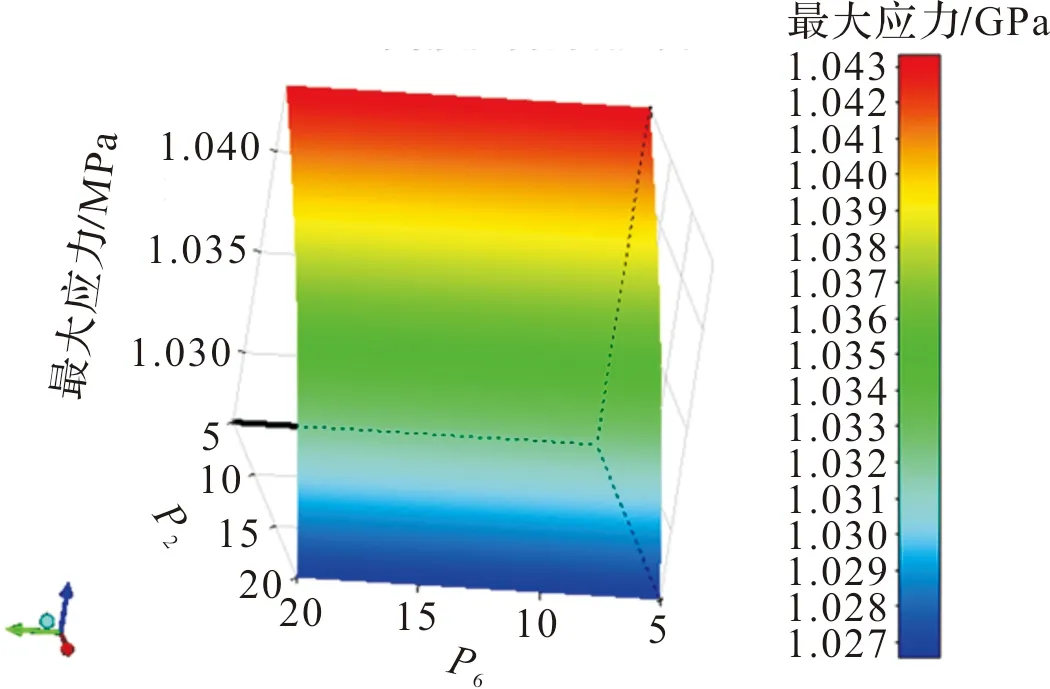
图12 参数P2，P6与最大应力的响应图

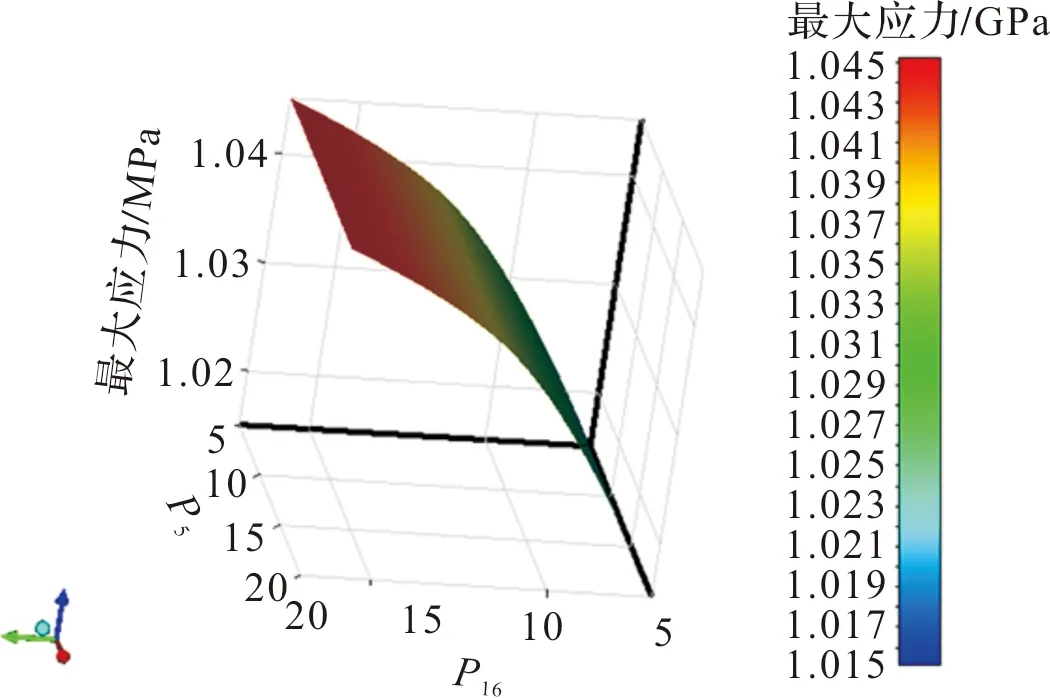
图13 参数P5，P16与最大应力的响应图

4.5 响应面优化

得到响应面后，根据响应面进行优化，将最大变形和质量的期望设置为最小，最大应力的期望设置为最大且小于1 014.3 MPa，计算得到3个候选结果，选取其中变形最小的结果作为最优结果(见表3)，优化后加强筋的布置方案如图14所示。对优化后的尾翼进行静力学分析，其最大变形为4.818 mm，最大应力为1 005.6 MPa，质量为4.659 kg，其应力和变形云图如图15、图16所示。

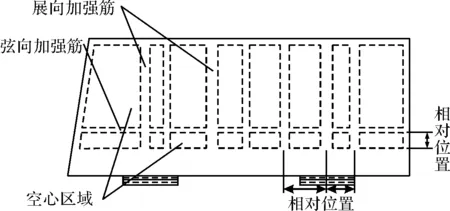
图14 优化后加强筋布置方式

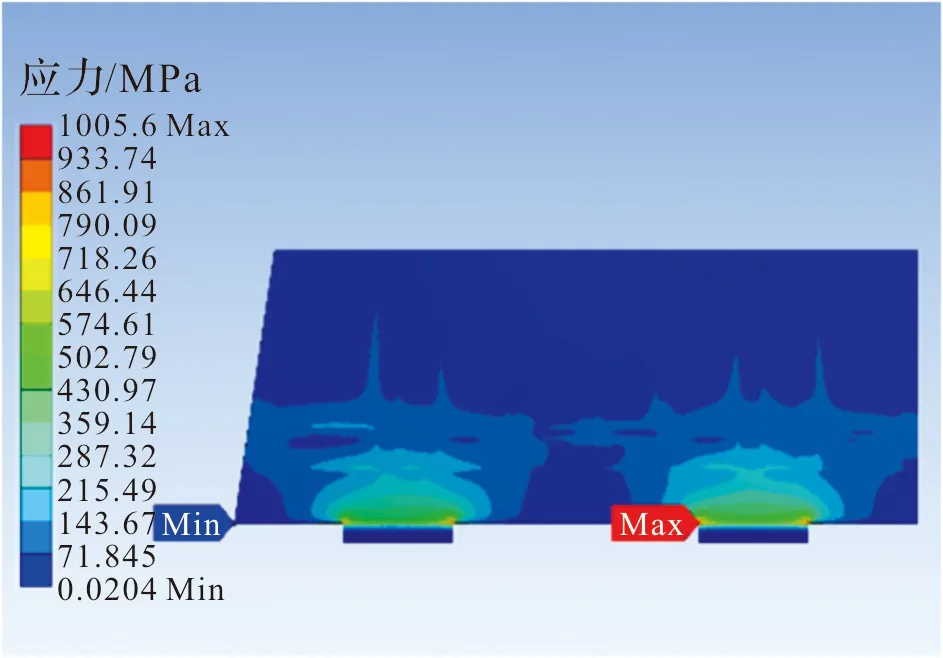
图15 尾翼优化后应力云图

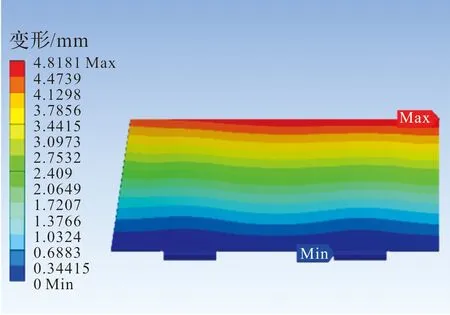
图16 尾翼优化后变形云图

表3 参数优化结果 单位:mm

根据计算结果，比较实心尾翼、均匀加筋尾翼和加筋且优化尾翼的有限元计算结果，见表4。可知，经过中空且以均匀方式加筋后，尾翼最大变形增加4.34%，最大应力增加0.61%，质量减轻21.04%；对加强筋的相对位置和宽度进行优化后，尾翼最大变形增加4.42%，最大应力减小了0.86%，重量减轻25.67%，虽最大变形有所增大，但增量小于5%，满足工程要求；轻量化效果较为可观。

表4 优化结果

5 结论

对某实心导弹尾翼进行了轻量化设计，得出了以下结论：

1)对尾翼的有限元分析，得到了与实际相符合的尾翼应力分布和变形情况，同时也发现该设计存在冗余。

2)去除冗余材料，参照飞机机翼内部梁、肋加强结构，对空心区域进行补强，在工程许可范围内，能有效降低结构的重量。

3)根据响应面对加强筋尺寸和位置进行优化，能进一步降低实心的弹翼质量，为实心弹翼的轻量化提出了一种设计思路。

4)通过CAE软件进行仿真实验，提高了设计的效率，具有较好的推广价值。