基于SVR的含缺陷管道剩余强度研究*

孙宝财，朱蔡文，凌 晓

(1.甘肃省特种设备检验检测研究院，甘肃 兰州 730050；2.武威中石油昆仑燃气有限公司，甘肃 武威 733000；3.兰州理工大学 石油化工学院，甘肃 兰州 730050)

0 引言

油气管道是我国国民经济建设的重要基础设施。截至2020年底，我国长输管道总里程已达14.4×104km[1]，一旦发生管道事故，将会给企业、环境以及人身安全造成巨大威胁[2]。统计表明，腐蚀缺陷是导致油气管道事故的主要原因之一[3]，因此，全面、及时、准确地预测含缺陷管道的剩余强度，对保障油气管道安全运行具有重要意义[4]。

针对含缺陷管道剩余强度预测分析，国外出台一系列标准公式对管道失效压力进行预测[5-9],但计算得到的管道剩余强度与试验数据误差较大，研究人员开始尝试使用有限元方法对含缺陷管道剩余强度进行仿真模拟，预测精度有所提升，但有限元方法需针对管体数据的不同重新建模，难以应对数据量较大的情况[10-12]。随着计算机技术的发展，机器学习得到广泛应用，本文结合支持向量回归(SVR)和管道爆破试验数据，建立含缺陷管道剩余强度预测模型，并对该模型的性能进行分析验证。

1 SVR理论基础

SVR是支持向量机在回归方面的应用，SVR在线性函数两侧建立1个“间隔带”，对于所有落入间隔带内的样本均不计算损失，对间隔带之外的样本计入损失函数，然后通过最小化间隔带的宽度与总损失以最优化模型[13-14]。SVR网络拓扑示意如图1所示。

图1 SVR网络拓扑示意Fig.1 Schematic diagram of SVR network topology

SVR通过寻找最优超平面，使所有训练集样本离该平面的距离最小(误差最小)，从而实现回归预测[15]。设含有l个样本的训练集为{(Xi，yi)，i=1，2，…，l}，其中{Xi=[xi1，xi2，xi3，…，xin]T，xi∈Rn}是第i个训练样本的输入向量，{yi∈R}为对应输出值。对于复杂的非线性回归问题，可通过映射变换将原始变量变换到高维特征空间，从而在高维特征空间中构造线性回归函数并求解。线性回归函数如式(1)所示：

f(X)=WTφ(X)+b

(1)

式中：W为可调的权值向量；φ(X)为非线性映射函；b为常数。忽略小于ε的拟合误差，则∈-SVR可以表示为式(2)所示的约束优化问题：

(2)

(3)

式中：a和a*为对偶变量；K(Xi，Xj)=φ(Xi)Tφ(Xj)。

2 模型评价方法

为验证基于SVR的含缺陷管道剩余强度预测模型的实际性能，本文选用相对误差(RE)、平均相对误差(MRE)以及决定系数(R2)分析对比模型的预测效果。其中，RE和MRE数值越小越好，其值为0时证明预测值与真实值相等；R2值越接近1拟合效果越好。RE、MRE、R2如式(4)～(6)所示：

(4)

(5)

(6)

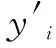
3 实例应用

3.1 数据来源

本文选用文献[16]中采集的60组含缺陷管道爆破试验数据，每组数据包含8种类型，分别为管道外径、壁厚、缺陷长度、缺陷深度、缺陷宽度、屈服强度、拉伸强度以及失效压力。随机选取该试验数据集中49组数据进行学习训练，剩余11组数据测试验证模型的预测效果。因数据较多，仅展示部分含缺陷管道爆破试验数据，见表1。

表1 部分含缺陷管道爆破试验数据Table 1 Partial blasting test data of pipeline with defects

3.2 数据预处理

为避免数值问题加快SVR收敛速度，在进行训练之前对所有数据进行归一化操作。将数据归一化至区间[-1,1]，部分归一化结果见表2，归一化公式如式(7)所示：

(7)

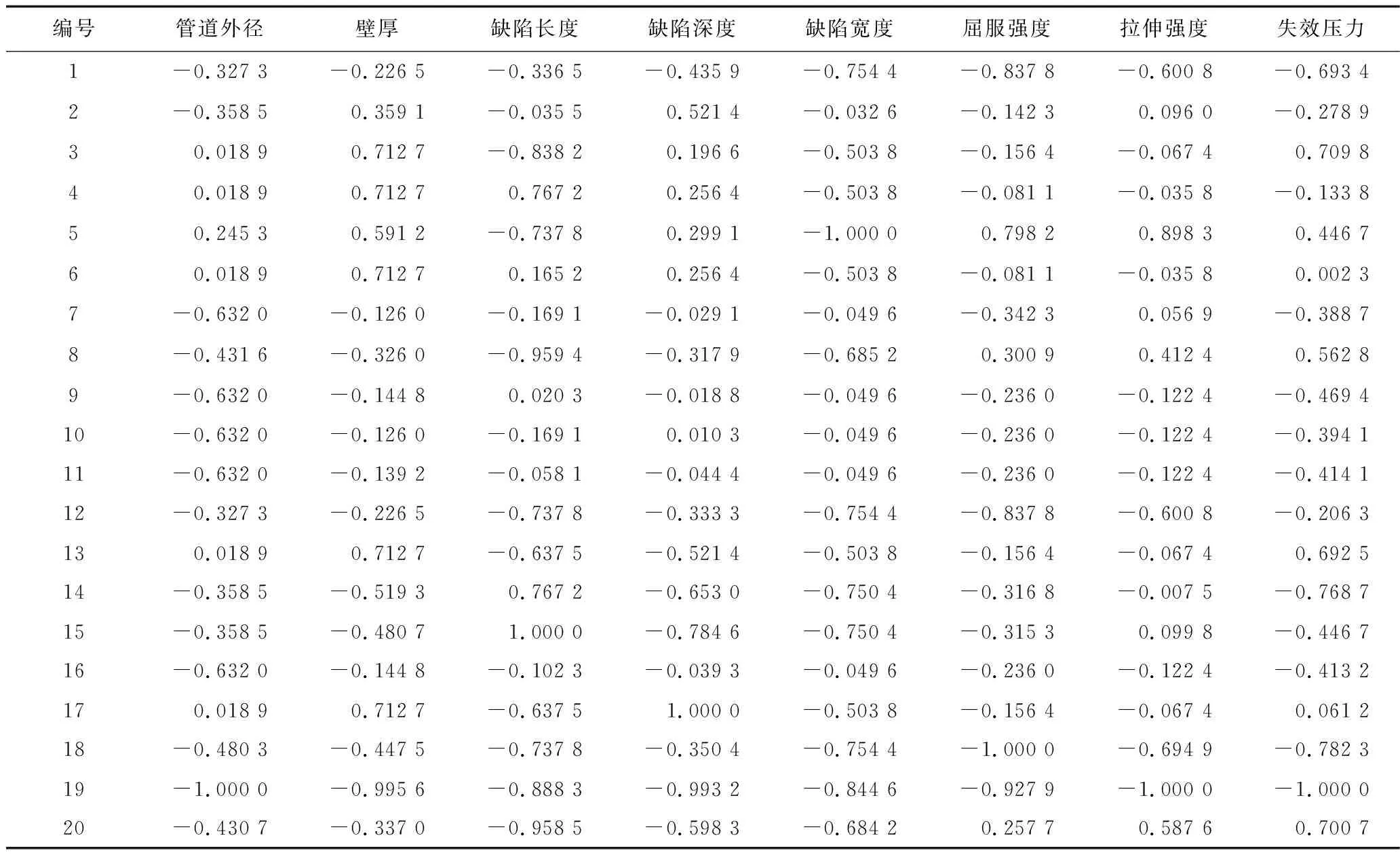
表2 归一化数据Table 2 Normalized data

式中：xnormalization为归一化结果；xmin、xmax为归一化区间临界值。

3.3 SVR初始参数设置

利用Matlab对SVR模型进行编程仿真模拟，并对SVR模型初始参数进行设置，其中核函数使用径向基核函数，惩罚因子c通过优选设为45.254 8，方差g设为0.176 8，损失函数值设为0.01。

3.4 模型预测结果分析

使用训练好的SVR模型对含缺陷管道剩余强度进行预测，预测结果见表3，训练集预测结果对比以及测试集预测结果对比如图2～3所示。预测结果相对误差统计见表4。由表4可知，使用训练好的SVR模型预测训练集数据时，最小相对误差为0.02%，最大相对误差为13.65%，平均相对误差为1.99%，证明文内训练的SVR模型较好地拟合出含缺陷管道剩余强度与其影响因素间的非线性关系。使用训练好的SVR模型预测测试集数据，预测结果的最小相对误差为0.55%，最大相对误差为10.35%，平均相对误差为2.63%，证明该模型具有广泛的适应性，并进一步验证基于SVR的含缺陷管道剩余强度预测模型具有较强的鲁棒性，应用该模型对含缺陷管道剩余强度进行预测，可为管道检维修和运行调度提供决策支持。由图3可知，使用训练好的SVR模型预测训练集数据时，除个别点外，预测值较好地逼近实测值，预测误差较小。由图3可知，预测结果除点7外均能较好地逼近实测结果，进一步验证预测模型的准确性。点7的预测结果未能准确地逼近实测值，这是由于训练SVR的数据较少导致。

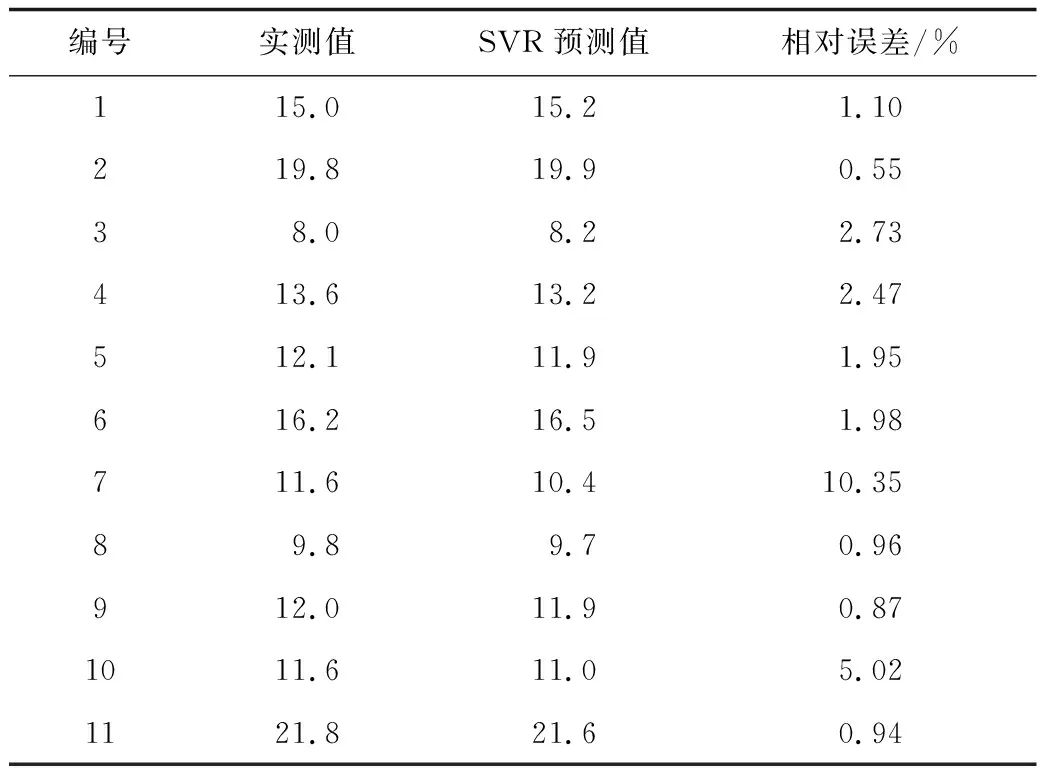
表3 测试集预测结果Table 3 Test set prediction results

表4 预测结果相对误差统计Table 4 Relative error statistics of prediction results %

图2 训练集预测结果对比Fig.2 Comparison on prediction results of training set

图3 测试集预测结果对比Fig.3 Comparison on prediction results of test set

分别将训练集和测试集的预测数据做线性拟合，得到训练集预测结果与实测值拟合如图4所示。由图4可知，拟合得到的一元一次方程为Y=0.979 5X+0.187 3，R2=0.990 3，验证基于SVR的含缺陷管道剩余强度预测模型具有较高的预测精度。测试集预测结果与实测值的线性拟合如图5所示。由图5可知，拟合得到的一元一次方程为Y=1.026 7X-0.549 2，R2=0.990 1，证明SVR模型不仅对训练集有较高的预测精度，而且对测试集的数据也可以无限逼近，这进一步验证模型的鲁棒性和准确性。

图4 训练集预测结果线性拟合Fig.4 Linear fitting on prediction results of training set

图5 测试集预测结果线性拟合Fig.5 Linear fitting on prediction results of test set

4 结论

1)基于SVR建立含缺陷管道剩余强度预测模型，预测结果最小相对误差为0.55%，最大相对误差为10.35%，平均相对误差为2.63%，其R2达到0.990 1，证明该模型具有较高的预测精度。

2)SVR模型预测含缺陷管道剩余强度可为管道的检维修和运行调度提供辅助决策支持。