重大件货物海上运输的惯性力分析

杨红莹， 朱仁传， 杨云涛， 俞赟,3

(1.上海交通大学 海洋工程国家重点实验室， 上海 200240； 2.中国船舶科学研究中心，江苏 无锡 214082； 3.中国船舶及海洋工程设计研究院， 上海 200011)

重大件货物形状不规则、单件较重。货物在运输过程中受到由于波浪和风作用引起船舶运动所导致的惯性力、自身重力、甲板支持力、风吹袭力及波浪飞溅力等作用，易产生滑移和倾覆的可能。船舶加速度是作为校核载于船上货物系固有效性的重要依据，故在系固系统设计之初，需要准确计算货物相对于船舶运动的惯性力。

目前货物惯性力计算主要有2种方法。第1种为经验公式法，根据许多研究机构以实船和船模加速度测试和数据分析为基础提出在设定恶劣海况下确定加速度值的经验公式计算方法。譬如，国际海事组织《货物积载与系固安全实用规则》(简称IMO CSS规则)、挪威船级社《船舶建造与入级规范》等。第2种方法为理论计算方法，基于船舶线性系统根据船舶运动响应函数与海浪谱求解船舶在海浪中的运动谱，由刚体运动方程得到船舶任意位置的运动统计值，即可得到货物重心处惯性加速度统计值。

很多学者针对规范公式展开了研究，邱文昌等[1-2]研究了6种不同规范船舶加速度计算公式，通过实例分析了不同规范的准确性和适用范围。吕瑶等[3]研究了《CSS规则》中加速度系数取值的计算模型，通过试算找出了计算模型中的参数设定值。宋巍[4]研究了《CSS规则》、中国船级社、挪威船级社的船舶入级规范以及传统方法船舶加速度计算公式，并分析了在实际应用中的优缺点。一些研究从理论角度出发，沈华[5]基于船舶运动理论，由假设船舶各自独立的横摇、纵摇和垂荡运动引起的惯性力线性叠加，系统地推导了重大件货海运的惯性力计算方法。

为研究重大件货物在海上运输时的惯性力，本文基于频域混合格林函数法和波浪谱分析方法，综合考虑海况、浪向角等环境因素和船舶航速、货物位置等船舶因素影响，对集装箱系列船舶在波浪中的惯性加速度进行不同工况下的短期预报，在系统梳理规范的基础上提出惯性加速度规范修正公式，为评估系固方案安全性提供技术依据。

1 经验公式法

经验公式法即采用各部位基本加速度值计算货物惯性力的各个分量或根据经验公式计算出六自由度运动周期和幅值，进而计算出货物在横向、纵向和垂向上的惯性力，适合常规船型。

1.1 IMO CSS规则

IMO编制的《货物积载与系固安全操作规则》采用了船级社协会多年前的一个数学模型，用于计算船载货物因船舶运动而产生的加速度，同时考虑了船舶浪中失速及船在恶劣海况时艏向的变化[6]。

1.1.1 惯性力计算

货物在惯性力的作用下会产生惯性加速度，分为纵向、横向和垂向3个方向。因此，惯性力在各个方向上的分量为：

F(x,y,z)=m(ax,ay,az)

(1)

式中：ax为纵向加速度(包含货物重力分量)；ay为横向加速度(包含货物重力分量)；az为垂向加速度(不含货物重量的静力部分)。

1.1.2 惯性加速度计算

基本加速度也分为纵向、横向和垂向3个方向：

(2)

式中：k1、k2分别为航速修正系数、横向稳性高度修正系数；ax0、ay0、az0分别为在不同装载位置时纵向、横向、垂向基本加速度值。

假设船长L=100 m，航速V=15 kn，方形系数Cb=0.7，25 d为一个航次，B/GM≥13(B为型宽，GM为初稳性高度)，无限航区全年运营，则基本加速度值ax0、ay0、az0见文献[6]。

若船长并非100 m且服务航速并非15 kn，k1应根据公式修正加速度值：

(3)

对于B/GM<13的情况，k2应按文献[6]对横向加速度值进行修正。

1.2 局限性

IMO CSS规则以图表形式直观确定了基本加速度的具体数值，运用方便，但也存在其局限性：

1) IMO CSS规则基于所设定恶劣天气、海况和船舶不利状况，但未明确给出所设定的船舶在航程中最大波高值或船舶的最大运动参数(如最大纵倾角、最大横倾角等)。

2) IMO CSS规则没有明确基本加速度图表中各个甲板的高度或者货物重心距离水线的实际距离，给实际应用造成一定困难。

3) IMO CSS规则计算方法在处理海浪问题时，采用不同海区进行统计平均的方法，缺少对可能出现的更高海况的估计。

4) IMO CSS规则基本加速度图表中未考虑计算货物重心横向位置的影响。

2 理论计算法

考虑船舶在波浪中各运动之间的耦合作用及相位变化，根据混合格林函数法计算其附加质量、阻尼及波浪扰动力，根据耐波性运动理论得到船舶运动，该方法适合于常规及非常规运输船装运大型货物时惯性力的计算。

2.1 有航速船舶在规则波中的运动响应

混合格林函数法通过引入假想的直壁控制面将流场分割成内域和外域，分别引入Rankine源和自由面格林函数并结合控制面上的连续条件对频域边值问题进行求解，兼顾了Rankine源的函数简单、灵活计算和自由面格林函数离散量小等两者的优点[7]。

假定流体理想不可压，流动无旋，根据势流理论，非定常速度势可以分解为入射势、各模态的辐射势、绕射势。入射波已知，辐射势和绕射势满足的控制方程和初边值条件为：

(4)

流域划分如图1所示，内域由船体湿表面Sb、内自由面Sf和控制面Sc组成，记作域Ⅰ；外域由控制面Sc、外自由面和远方辐射面S∞组成，记作域Ⅱ。

利用域Ⅰ、域Ⅱ的边界积分方程，将不同边界上的条件代入，可求解得到整个流域内的水动力系数μij、λij。

根据船体的线性频域运动方程：

(5)

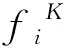
2.2 不规则波中惯性加速度预报

根据不规则波理论和平稳随机过程的谱分析方法[8]，在不规则波中的船舶重心位置处运动短期预报可表示为:

(6)

式中：Hs为有义波高；T1为特征周期；Sζ(ωe|Hs,T1)为短期海况分布(Hs,T1)下的海浪谱；Si(ωe|Hs,T1,θ)为不同浪向角下的各模态运动响应谱；RAOi(ωe|θ)为不同浪向角下各模态运动响应幅值因子，包括位移、速度和加速度。

对于船舶上任意位置的垂向、横向和纵向方向的运动位移、加速度响应分别为：

(7)

(8)

3 多元线性回归

3.1 多元线性回归模型

多元回归分析是一元回归分析的扩展，当影响因变量的因素多于一个时，需要建立多元回归模型。设随机变量与一般变量的线性回归模型为：

y=β0+β1x1+β2x2+…+βpxp+ε

式中：x1,x2,…,xp是p个可以精确测量并控制的一般变量，即自变量；y是因变量；β0,β1,β2,…,βp是个p+1个未知参数，β0为回归常数，β1,β2,…,βp为回归系数，ε～N(0,σ2)为模型随机误差。

3.2 回归方程分析

关于回归方程拟合效果的分析，主要从2个方面进行：

1) 相关系数分析:

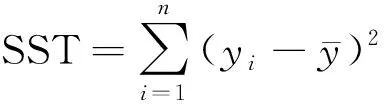
2) 标准误差。误差项方差σ2的无偏估计为：

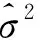
3.3 回归方程的检验

3.3.1 回归方程的显著性检验

检验自变量x1,x2,…,xp的全体对因变量少是否有显著影响，最常用的整体性检验方法仍是方差分析方法。

1)F检验：

当F>F1-α0(p,n-p-1)，即认为因变量y与自变量x1,x2,…,xp之间显著地有线性相关关系；否则认为因变量与自变量之间线性相关关系不显著。

2) 显著性概率P=P{F(p,n-p-1)>F}：

在显著性水平α下，当α>P时，即认为回归方程有显著意义。

3.3.2 回归模型的假设检验

线性回归模型满足假设的前提，其模型才是合理的。其中假设包括：

1) 误差ε服从正态分布；

2) 多重共线性检验；

3) 线性相关性检验；

4) 误差项ε的独立性检验；

5) 方差齐性检验。

4 数值计算

4.1 规则波中运动响应数值计算

为验证混合格林函数法的准确性，以集装箱船KCS为例，进行了不同航速下数值计算并与以航速修正法为原理的部分势流软件计算结果以及试验值进行了比较。KCS是由KRISO研究所设计的一艘集装箱船，存在许多公开的试验数据[9]，其主尺度参数如表1所示。船体网格划分如图2所示，在艏艉2端网格加密，数值计算结果见图3、4。

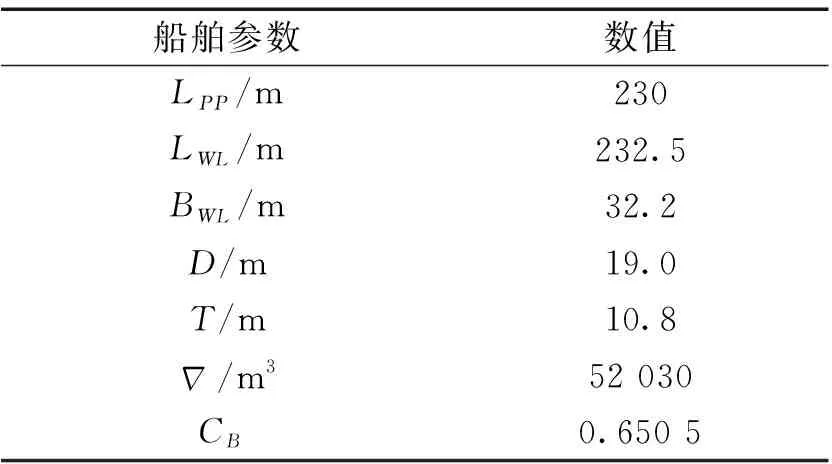
表1 KCS主尺度参数Table 1 Main particulars of KCS model

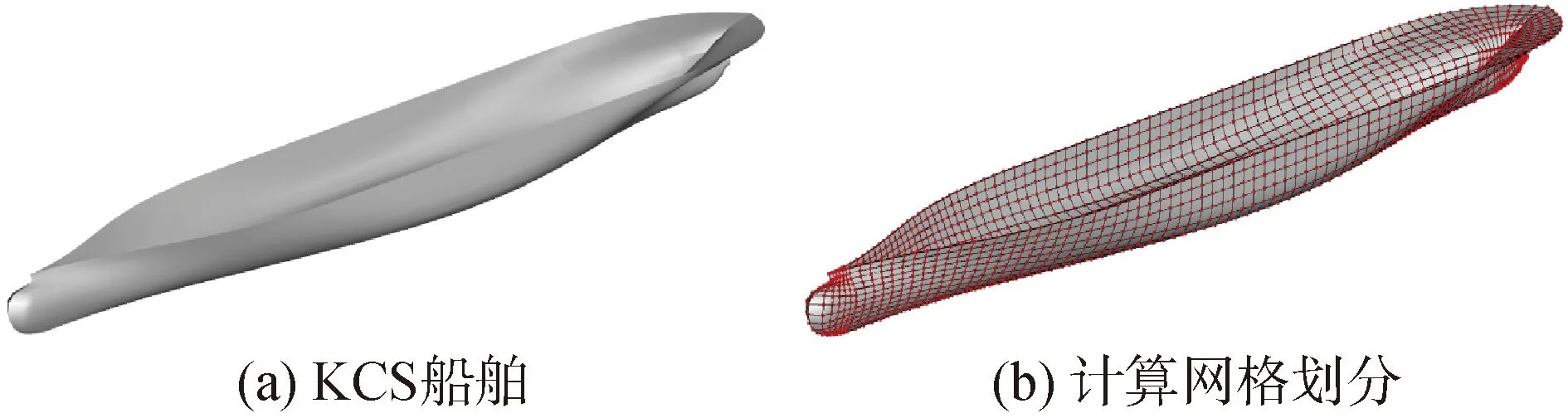
图2 KCS船舶与计算网格划分示意Fig.2 KCS container ship geometry and computational mesh

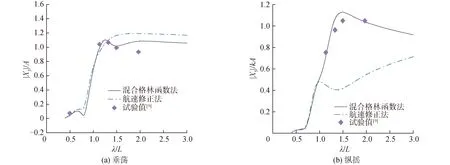
图3 KCS在迎浪下垂荡、纵摇运动响应RAOFig.3 Transfer functions for heave and pitch as function of wave length

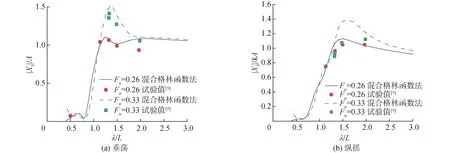
图4 KCS迎浪不同航速时垂荡、纵摇运动响应RAOFig.4 Transfer functions for heave and pitch as function of wave length in different speeds

根据KCS在Fr=0.26时迎浪下的垂荡和纵摇运动响应RAO可看出，混合格林函数法对于有航速船舶的运动响应计算相较于航速修正法与试验值更接近，在不同航速下数值结果与试验值吻合较好。

4.2 不规则波中惯性加速度预报

在波浪中由于船舶运动产生的对货物垂向、横向及纵向的惯性加速度，其大小与海况、计算位置、航速及浪向有关。为研究不同工况下的惯性加速度，以KCS为例，选择5种航速、7种浪向、7种海况和50个计算位置进行数值理论计算，具体见表2。计算位置示意见图6。

表2 计算工况参数Table 2 Parameters of calculation conditions

根据航行海域情况选择充分发展海浪的ITTC双参数谱[8]，其波浪谱密度曲线见图5。

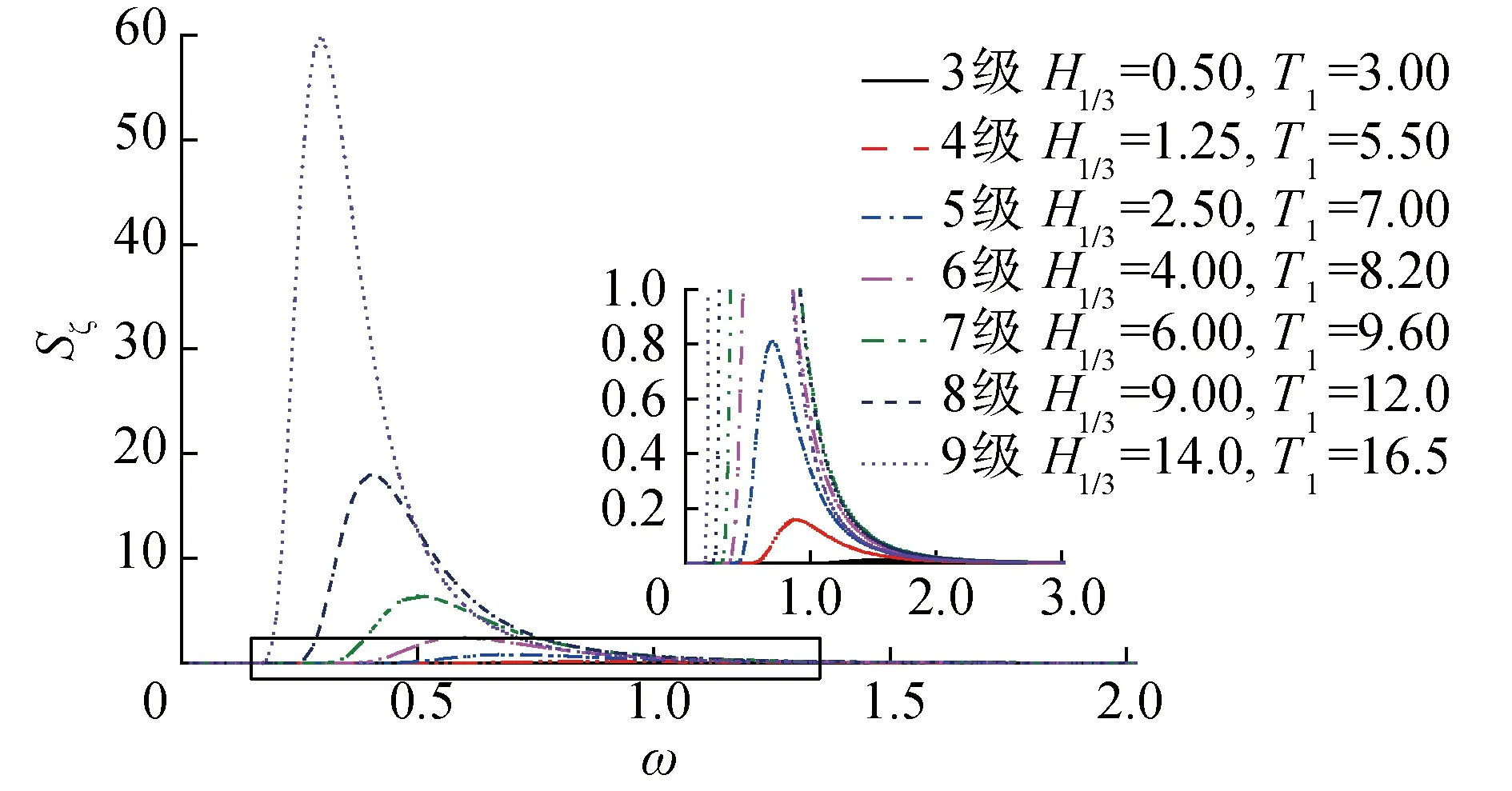
图5 ITTC双参数谱Fig.5 ITTC two-parameters

图6 货物计算重心位置Fig.6 Position of cargo center of gravity

为研究惯性加速度随计算位置坐标变化，选取甲板中心线上0.1～0.9LPP位置、船舯-0.3～0.3B位置、中心垂线0.1～0.9D位置进行计算。

图8为KCS在Fr=0.26和9级海况时理论计算结果与IMO CSS经验结果在不同浪向角下随计算位置的变化曲线图。可以得到以下结论：

1) 理论值随计算位置的变化：垂向加速度随x坐标变化最明显，艏艉值明显高于船中；横向加速度随x坐标变化较小，艏艉值较船舯略高。纵向加速度随z坐标变化强烈，随z坐标成线性变化增加；纵向加速度随y坐标的变化取决于浪向角，艏斜浪时左舷值高于右舷值，艉斜浪则相反。

图7 浪向角Fig.7 wave angles

2) 通过在最高海况下理论值与经验值的比较，理论计算横向加速度高于经验公式值，且随着垂向高度的增加，两者差距减小；而理论计算得到的垂向加速度和纵向加速度均小于经验公式值。

5 回归分析

根据各机构规范中惯性加速度值的经验公式：1)中国船级社《钢质海船入级与建造规范》(简称CCS钢规[10])。2)美国船级社《RULES FOR BUILDING AND CLASSING STEEL VESSELS》(简称ABS钢规[11])。3)挪威船级社《RULES FOR CLASSIFICATION OF SHIPS》(简称DNV规则[12])可知，船舶任意位置的纵向、横向和垂向惯性加速度可表示为6自由度运动加速度及其分量的线性函数：

(9)

式中：

asway=3a0c

aheave=a0=aH1/3(b+(1-cosα))

apitch-x=fa0zrpL0.82

aroll-y=da0zrp

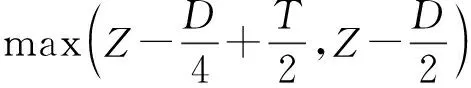
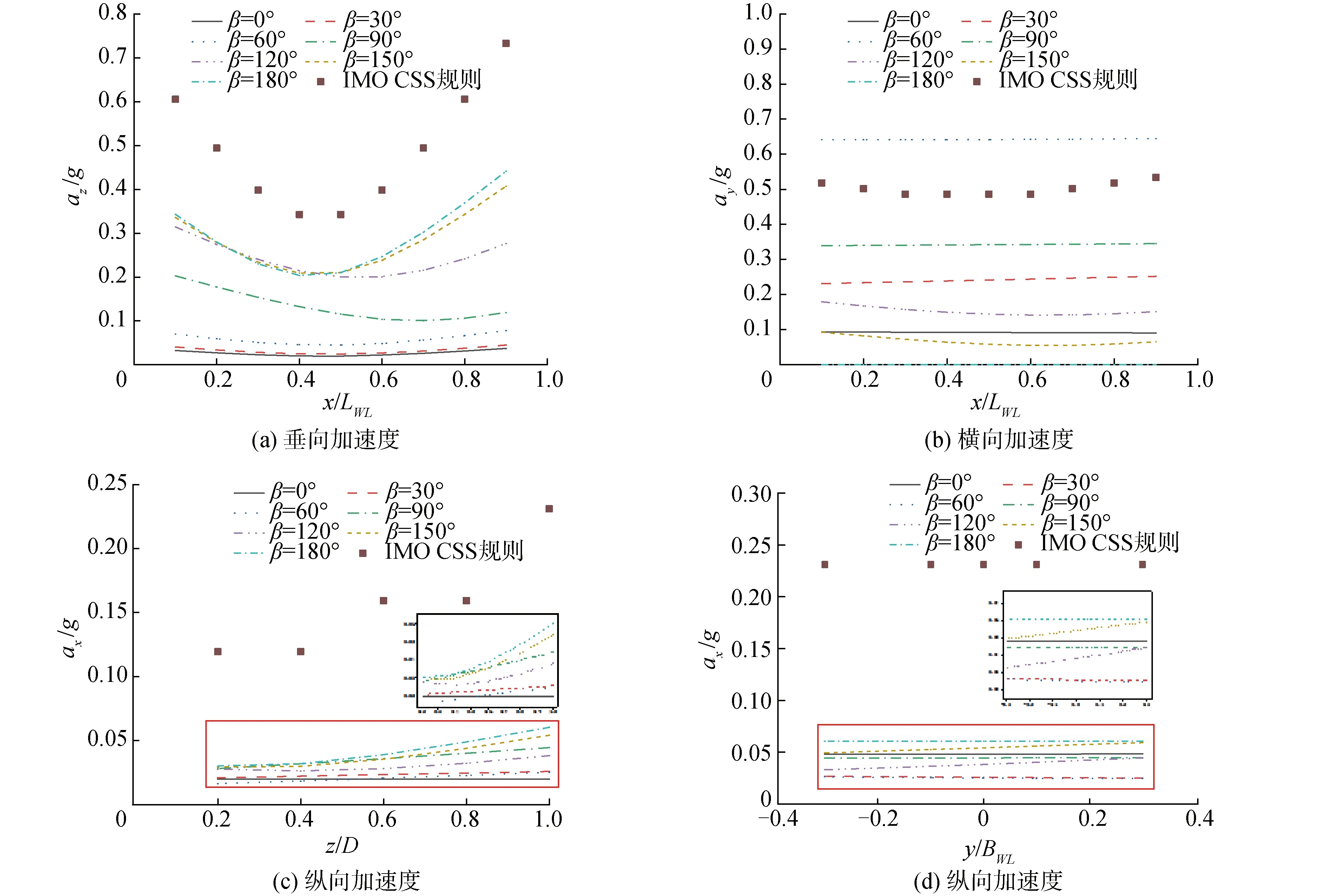
图8 不同计算位置的加速度理论值与经验值比较Fig.8 Comparison of theoretical and empirical acceleration values at different calculation positions

5.1 建立回归模型

以垂向加速度线性回归分析为例，建立回归模型过程如下：

1) 根据研究目的收集数据和预分析。

以KCS为母型船进行船型变换得到不同尺度的14艘集装箱船舶系列，使得LPP在200～300 m、L/B在6～8.5、Cb在0.6～0.7、GM在1.0～10 m变化。采用上述方法，对每一艘船舶在不同工况下惯性加速度进行短期预报值，并完成对数据的筛选和清洗。

2) 根据线性关系建立基本回归模型。

由散点图可知，垂向加速度与垂荡加速度、纵摇加速度分量之间存在较强的线性关系，与横摇加速度分量线性关系较弱。建立多元线性回归模型进行回归分析，其回归残差图与结果如图9、10所示。

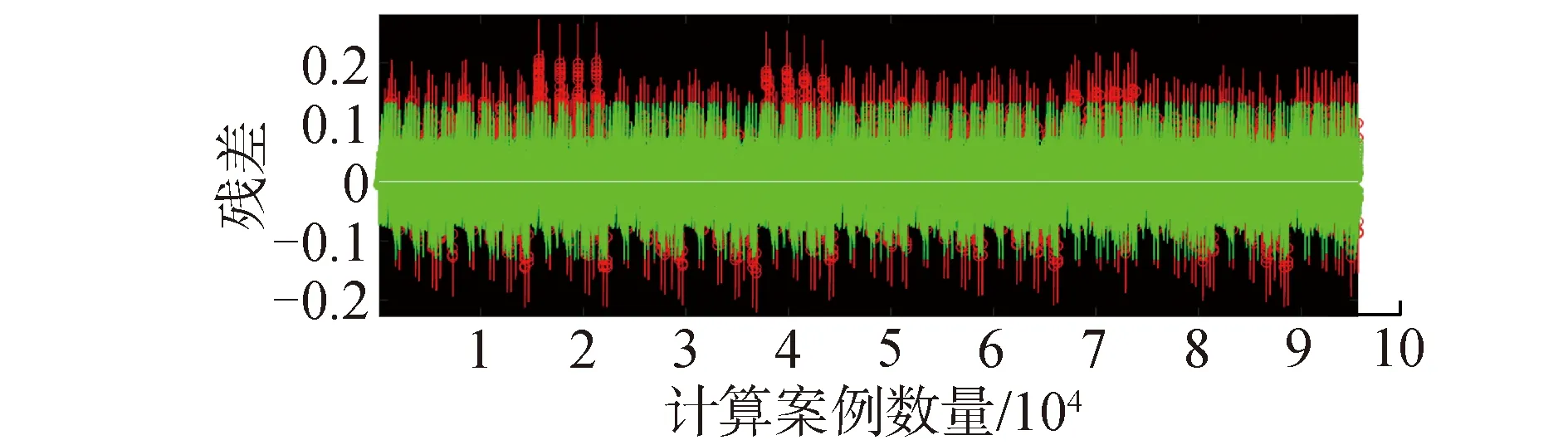
图9 残差图Fig.9 Residual plot

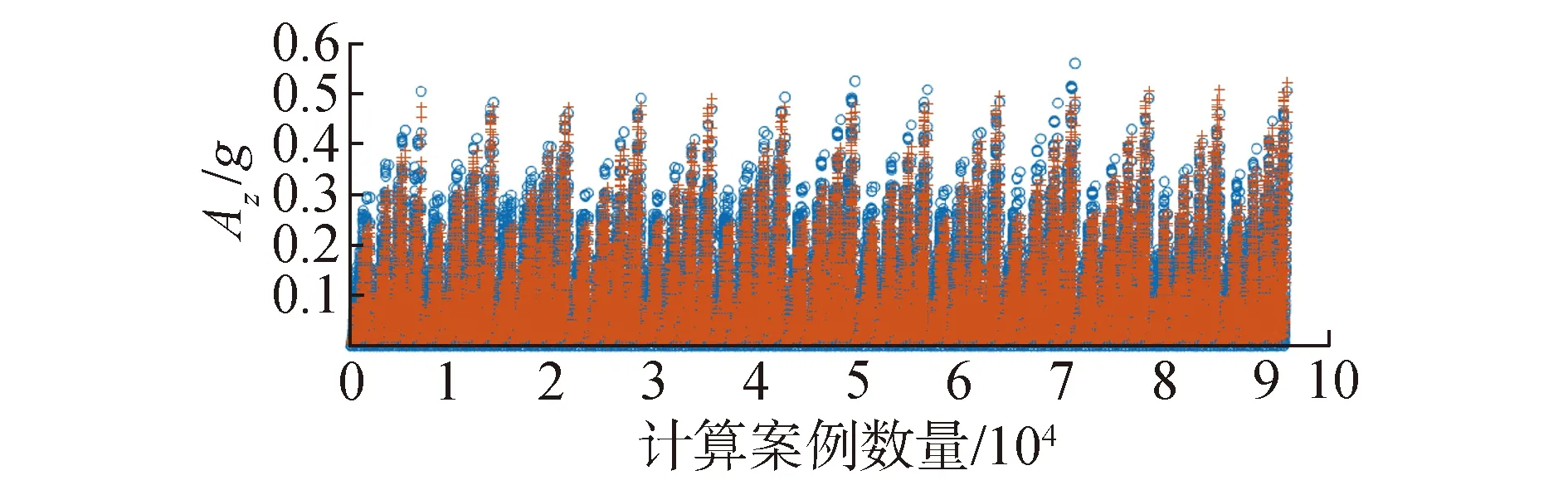
图10 预测值与实际值的比较Fig.10 Comparison of predictive values and actual values

3) 模型的精细分析。

由表3回归系数可得：

①相关系数的评价：一般相关系数绝对值在 0.8～1内，可判断回归自变量与因变量具有较强的线性相关性。本文R2的绝对值为0.831 7，表明线性相关性较强。

②回归系数的评价：回归系数置信区间不包含零点、残差在零点附近表示回归模型较好。

5.2 回归模型检验

以垂向加速度回归模型为例进行检验。

5.2.1 回归方程的显著性检验

1)F检验：

F=1.638 7×105>F1-0.05(3,95 650-3-1)=2.605 0

2)P值检验：本例输出结果P<0.000 1,显然满足P<α0=0.05。

表3 垂向加速度回归系数Table 3 Regression coefficients of vertical acceleration

5.2.2 回归模型的假设检验

1) 误差ε服从正态分布。

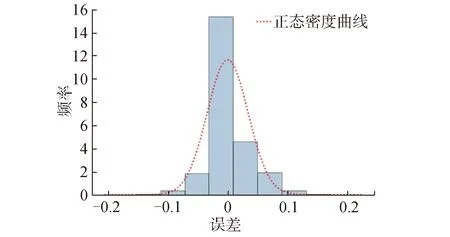
图11 误差的正态分布曲线Fig.11 Normal distribution curve of residuals

2) 多重共线性检验。

多重共线性可利用方差膨胀因子VIF判断：若VIF大于10，则说明变量间存在多重共线性；若 VIF大于100，则表明变量之间存在严重的多重共线性。经计算，各变量aheave、apitch-z、aroll-z的方差膨胀因子VIF分别为1.851 0、2.117 5、1.043 5。

3) 线性相关性检验。

线性相关性指模型的因变量和自变量之间存在线性相关关系，利用Pearson相关系数判断：各变量aheave、apitch-z、aroll-z的Pearson相关系数分别为0.882 4、0.880 3、0.226 9。

4) 误差项ε的独立性检验。

残差ε的独立性检验通常利用Durbin-Watson统计值来测试。在本次回归中计算所得DW值为2.003，表明残差之间不相关。

5) 方差齐性检验。

方差齐性要求模型残差项的方差不随自变量的变动而呈现某种趋势。

经过回归模型检验后，集装箱船的惯性加速度经验公式可修正为：

ax=0.001 6+0.098 6asurge+0.019 7apitch-x+
0.037 3gsinθ
ay=0.000 43+0.000 7asway-0.000 025aroll-y+
0.091 0gsinφ
az=0.006 4+2.024 2aheave+5.565 3apitch-z+
0.220 5aroll-z

图12 方差齐性检验Fig.12 The test of homogeneity of variances

6 结论

1) 在最恶劣海况下横向加速度经验公式值偏小；垂向加速度经验公式值略微大于理论计算值；纵向加速度经验公式值远大于理论计算值，裕度足够。理论计算方法综合考虑了船舶参数与海浪环境的影响，计算结果相对准确。

2) 本文提出的经验修正公式中考虑了具体海况参数的影响，即有义波高和航行浪向的修正参数；考虑了不同货物重心计算位置的影响，即X、Y、Z的修正影响。本文总结了系列集装箱船计算模型的经验修正公式，相对于原经验公式适用范围增大，且精确度提高。目前仅适用于集装箱船舶惯性加速度计算，可为其他船舶相关计算提供参考。