传感器网络DoS攻击下随机系统的故障检测设计

刘一帆， 左稳， 张之津， 田英鑫， 高亚斌

(1.北京空间飞行器总体设计部， 北京 100094； 2.哈尔滨工业大学 航天学院, 黑龙江 哈尔滨 150001)

无线传感器网络在基础设施安全、城市管理、智能交通、工业自动化、环境与人居监测以及军事等领域具有重要应用前景,是目前网络化工业系统的研究热点之一[1-3]。与有线通信系统相比,无线传感通信系统可以大大降低传感基站安装和维护的成本并节省相应的时间。更重要的是,无线数据通信的方式可以提供无成本的重定位和动态移动性,还可以实现远程通信。因此,目前运用无线传感器网络对不同目标系统进行控制、滤波和估计的问题已经得到了广泛的研究[4-6]。虽然无线传感器网络在工程应用中有着巨大的优势,但是,因为其自身结构的复杂性和大规模的特点,所以传感器节点易遭受网络攻击,如常见的拒绝服务(denial of service, DoS)攻击等,为整个无线传感器网络的可靠性和安全性带来威胁。

另一方面,在现代信息技术时代,系统故障极大地阻碍了系统的运行,威胁了系统的稳定性和安全性。一般来说,在实际系统中,故障偏差可能发生在原系统、传感器、执行器或开关逻辑元件的某个单元中[7]。如果能够快速检测到这些软故障,则可以采取适当的措施来减少系统遭受的损失,以及避免严重的灾难。因此,为了避免故障引起的系统稳定性降低和系统性能下降,设计一种有效的故障检测方案是相当必要的[8-10]。近年来,针对由无线传感器网络构成的网络化系统出现了一些分布式估计和滤波方法。例如,Luo等[11]通过设置传感器发生故障的概率,将传感器故障引入到最优事件检测过程中,实现了无线传感器网络的分布式容错检测方案。Shames等[12]针对二阶线性互联系统提出了一种基于未知输入观测器的分布式故障检测方法。Ferrari等[13]针对一类大型动态系统,设计了一种分布式故障检测方法。然而,目前缺乏可行的方案和技术解决无线传感器网络DoS攻击下系统的故障检测问题。

基于以上事实,本文将研究无线传感器网络DoS攻击下一类随机系统的分布式故障检测问题,主要技术难点体现在以下几点: 1)根据具有DoS攻击的无线传感器网络特征,如何构造一种滤波器用于产生故障检测评估机制中的残余信号;2)如何确定所设计的滤波器的参数并解决参数耦合问题;3)在使用滤波器产生残余信号时,如何构造故障诊断逻辑。为此,本文将同时考虑系统中的参数和过程扰动及测量噪声,利用Bernoulli过程描述无线传感器网络中的传感器网络中的Dos攻击,通过构造一种增广的随机系统,利用Lyapunov函数法导出该系统稳定性判据并设计分布式滤波器的参数矩阵;最后,将所设计的故障检测方法应用到一种风力发电系统的变桨机构系统中。

1 系统建模与问题描述

1.1 系统与故障模型

设k∈{0,1,2,…}表示离散系统的第k个采样点,kT表示采样时刻,T表示(固定的)采样周期。考虑实际系统中可能出现的系统故障以及常见的外部干扰等不确定性,所构造的离散时间随机系统表示为:

x(k+1)=(A+ΔA(k))x(k)+Ex(k)ω(k)+

Bd(k)+Ff(k)

(1)

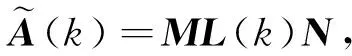
针对无线传感器网络,本文考虑系统对象(1)所配置的传感器网络拓扑是固定的,传感器网络中第i(i∈{1,2,…,N})个传感器节点通过对邻居节点(和自身)的数据收集,第i个传感器的数据表示为:

yi(k)=∑j∈NilijCjx(k)

(2)

式中：矩阵L[lij]N×N表示该无线传感器网络节点的拓扑结构,如果第i个节点可以从第j个节点收集数据,那么lij=1，否则lij=0。本文考虑传无线传感器网络节遭受DoS攻击的情况,即网络攻击者接入网络节点后通过消耗带宽资源或系统资源的方式进行DoS攻击,导致该传感节点收发数据异常,信号传输被中断。当没有发生DoS攻击时,信号恢复正常传输。因此,引入参数ξi,如果在第k时刻第i个传感器与下一个单元(滤波器)通信时受到DoS攻击,则ξi(k)=0,同时,该传感器的下一个单元(本文考虑滤波器作为其信号接收端)保持其最后一次测量其中ka为最后一次信号中断时刻,是表示第a次中断;否则,ξi(k)=1,即传感器的下一个单元的测量将更新为即时测量。那么,实际传输的测量表达式可表示为ξi(k)yi(k)。同时,考虑实际数据传输和测量过程中噪声干扰为ν(k)∈Rq,则第i个滤波器的实际输入为：

(3)

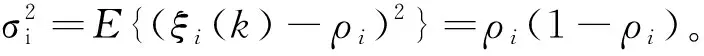
1.2 基于传感器网络的滤波器与评估函数构造

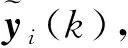
(4)

在故障检测系统中,通常需要参考残余模型来描述所期望的残余向量的特征。因此,对故障f(s)增补一个加权矩阵函数fw(s)=W(s)f(s),用以提高故障检测系统的性能。fw(s)=W(s)f(s)的状态空间实现可以表示为:

(5)

式中：f(s)和rf(s)分别是f(k)和rf(k)的Laplace变换。向量xr(k)∈Rw表示为参考模型的状态变量；rf(k)∈Rg表示参考信号。Ar、Br和Cr是常矩阵。

在故障检测过程中,残余评估器通常包括一个阈值和一个决策逻辑单元。残余评估函数用于评估生成的残余。在建立残余信号后,使用指定的评估函数计算残余评估值,并将其与预定义的阈值进行比较[8,14-16]。当评估值超过阈值时,将触发相应的警报。本文根据系统(1)建立第i个滤波器的阈值函数表示为:

(6)

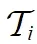
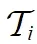
(7)

注意：残余评估器一般由残余评估函数和阈值构成。如果残余函数的计算值超过了预定义的阈值,则可以立即触发相应的报警,这意味着在此时刻检测到了故障。一般而言,采用观测器或滤波器来产生残余信号以实现进一步的故障诊断。本文所介绍的评价函数(6)是根据分布式滤波器产生的残余信号设计的,还有其他方法如观测器法可以用于产生残余信号并用于评估函数设计的方法。评估指标可参阅文献[6-8]。

1.3 全局动力学系统描述

式(8)中的矩阵定义为:

同时,其中的分块矩阵定义为:

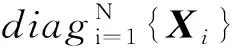
2 系统建模与问题描述

2.1 系统稳定性分析

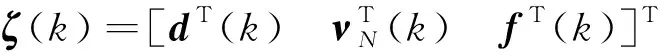
定义1考虑不确定随机系统(8)(ζ(k)=0)及其平衡点z*=0,如果其解z(k)满足:

式中z(k)是在初始条件为z(0)时系统(8)在k时刻的解,则不确定随机系统(8)为鲁棒均方渐近稳定的。

定义2如果不确定随机系统(8)是鲁棒均方渐近稳定的,且在零初始条件下可以得到:

‖e‖E2≤γ‖ζ‖E2, ∀0≠ζ∈2[0,∞)

(9)

式中‖e‖E2的定义为:

那么系统(8)是鲁棒均方渐近稳定且具有H∞干扰抑制水平γ>0。

针对上述故障检测系统(8),根据定义1,将利用Lyapunov稳定性理论首先导出该系统的稳定性条件,为滤波器参数设计提供依据。为此,定理 1给出了系统(8)的一种H∞意义下稳定性的判据。

定理1考虑式(8)中的动力学系统。如果存在矩阵P=PT>0以及正标量和γ,满足以下矩阵不等式:

(10)

其中矩阵Ξ的定义为:

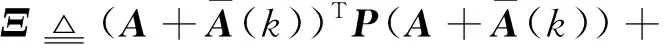
那么系统(8)是均方指数稳定的,并且满足式(9)中的H∞性能水平γ。

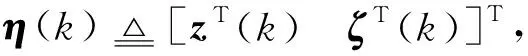
然后,根据式(8)中的动力学系统,通过对V(k)进行差分计算可以得到:

E{zT(k+1)Pz(k+1)}-zT(k)Pz(k)=

由此可以进一步得到:

另一方面,对于标称系统(8),此时系统(8)中不包含不确定项,即ζ(k)≡0,则根据式(10)中条件可得到如下式子成立:

Ξ-P+I+GTG<0

因此,E{zT(k+1)Pz(k+1)}-V(k)<0,∀z(k)≠0。也就是说,存在标量>0满足:对任意z(k)≠0有如下关系式成立:

E{V(k+1)}-E{V(k)}≤-E{‖z(k)‖2}

对上述不等式的两边从0到∞进行累加,得到:

E{V(∞)}-E{V(0)}≤-

即有以下不等式成立:

因此根据定义1 可知:如果系统参数满足定理1所述的条件(10),则可以得到随机系统(8)是鲁棒均方指数稳定的。证毕。

2.2 传感器参数设计

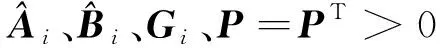
(11)

其中的分块矩阵定义为:

ΦεNTN+ϑ2P-2ϑI+

那么系统(8)是均方指数稳定的,并且满足式(9)中的H∞性能水平γ。

证明:根据矩阵P>0可知:对任意标量ϑ>0有(P-1-ϑI)TP(P-1-ϑI)≥0,即-P-1≤ϑ2P-2ϑ成立。因此,由条件(11)可以得到:

(12)

由此可知,根据条件(12)可以得到定理1中的稳定性判据,因此同样可以得到定理1的结论。证毕。

注意：观察条件(12)中可解的矩阵不等式,对该类故障检测滤波器参数矩阵的求解方法而言,现存的方法(如文献[17])大都采用锥补线性化程序。值得注意的是,对同等的矩阵不等式(组)而言,该程序为了达到一定的求解误差可能需要花费大量的求解时间。由于本文所提出的条件是严格的线性不等式组,因此无需线性锥补算法就可以直接求解,因而降低了计算复杂度。因此,本文所设计的基于分布式滤波的安全故障检测方法的步骤可以描述如下:

1) 根据系统模型(1),初始化该系统的参数;

2) 配置无线传感器网络节点,确定其拓扑结构L[lij]N×N;

3) 选取故障加权系统(5)及其参数;

4) 构造分布式滤波器(4),并根据定理2求解该滤波器参数;

5) 根据每个滤波器的输出建立评估函数(7)以及阈值函数(6);

6) 将所得滤波器接入系统中,系统运行时监测评估函数的变化,根据上述检测逻辑决定故障警报。

3 在风力发电系统中的应用

风力发电系统由于所处的环境复杂,发生故障的频率在实际中较为常见。例如2016年2月美国纽约Madison县Fenner风电场的1台1.5 MW风电机组发生叶片坠落事故;同月,我国河北省乌登山风电场110号风机倒塔,风电机组倒塔事故已经成为风电机组安全运行的最大隐患,而倒塔事故大部分是由于风电机组系统性故障引起。本节将考虑一种常见风力发电系统变桨机构模型,在Matlab中进行仿真验证所提安全故障检测的方法的有效性。

在风力发电系统中,液压变桨机构是一种能够通过调节叶片桨叶角使风力发电机正常运行的装置。当风速过大时,通过液压变桨机构使桨叶角变大,当风速变小时,通过液压变桨机构使桨叶角变小。通过对液压变桨机构的调节可以使风力发电机捕获最大功率且降低波动,减少对风力发电机组装置的损害。液压变桨机构动力学系统模型为[18]:

式中：将输入βr考虑为外部输入d。在本例中,考虑δ=0.9以及ωn=3.42。另外,对每一个变桨机构叶片配置2个传感器,分别监测其桨叶角βj(k)和角速度βj(k+1)。因此,可以构建一个具有6个节点的无线传感器网络,其拓扑结构考虑如下:

此外,滤波器单元在获得每个传感器测量时,考虑测量噪声干扰为ν(k)=0.1 rand(k);考虑所配置的无线传感器网络节点遭受带宽消耗型DoS攻击,描述该DoS攻击过程的随机变量期望分别考虑为ξ1=0.6,ξ2=0.7,ξ3=0.8,ξ4=0.9,ξ5=ξ6=1。由于外部复杂环境对变桨机构的影响,考虑其中的参数摄动ΔA(k)和随机扰动ω(k)为:

在仿真中,考虑变桨机构常见的叶片老化或变形引起的角度异常导致的故障信号:

图1 传感器网络受到DoS攻击的情形Fig.1 The illustration of the sensor network under DoS attacks

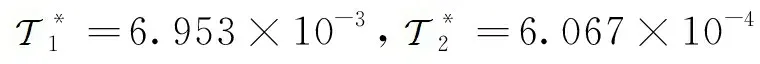
由图2可知,前4组滤波器尽管在传感器网络DoS攻击环境下仍能及时检测出故障,后2组在无DoS攻击下较快检测出故障,并且均在第23 s检测出了故障。根据第1.2节中所表示的警报逻辑规则,警报器将在21 s时触发并发出警报。因此,这些仿真结果表明了所设计的分布式滤波器成功地产生了其评估信号,并且尽管在DoS攻击下相应的故障检测机制仍然立即检测出了到变桨机构叶片故障,从而验证了所设计的安全故障检测方案的有效性。

注意：本文的故障检测方法是在文献[11-13]基础上的一种拓展研究,侧重研究DoS攻击下的系统故障检测问题,其优越性在于增加了对DoS网络攻击的可容许性和鲁棒性。此外,从留数信号产生的方法的角度来看,解决该故障检测问题的方法和技术目前较少,但是同样可以利用现有其他的技术拓展应用到该问题中,如可以基于Kalman滤波器或观测器技术来设计传感器网络DoS攻击下的状态估计算法用于评估函数和实现故障检测。

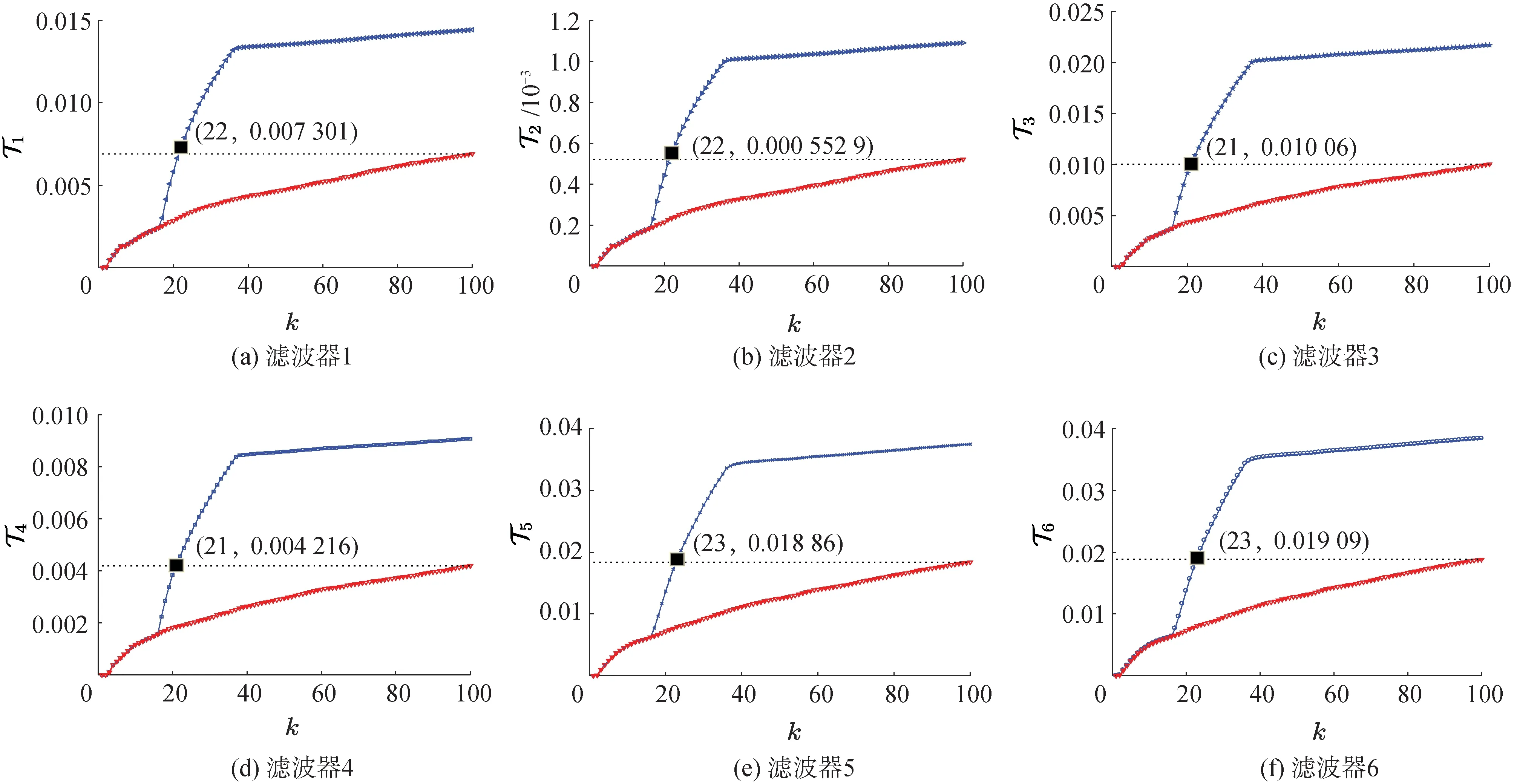
图2 6组评估函数的变化曲线Fig.2 Curves of the evaluation functions of filter 1～6

4 结论

1)故障检测是保证实际系统可靠运行的重要保障。本文所提出的基于分布式故障检测方案是一种应用于无线传感器网络环境下的系统故障检测方法，所设计的分布式滤波器对DoS攻击具有一定的防御性。

2)该滤波器参数可以通过提供的矩阵不等式条件求解和计算得到，与现有方法相比具有一定的便捷性。

3)该分布式故障检测方法在具有传感器网络配置的风力发电变桨机构系统中得到了有效验证，该方法中对应的滤波器和评估函数对故障检测检测单元具有明显的有效性。

为了拓展所提方法的广泛应用，未来将进一步考虑复杂不确定非线性系统，从而扩大该故障检测方法在实际系统中的应用。