基于反馈线性化的AUV三维轨迹跟踪滑模控制
李娟, 王佳奇, 丁福光
(1.哈尔滨工程大学 水下机器人技术重点实验室,黑龙江 哈尔滨 150001; 2.哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001)
自主式水下航行器(autonomous underwater vehicle,AUV)凭借自身的安全性以及经济性成为海洋勘测、港口侦察等任务的重要工具,AUV的航迹准确跟踪控制能力是执行这些任务的技术基础。
AUV三维轨迹跟踪控制一直是研究的热点,传统的非线性控制方法有反步控制[1-3]、滑模控制[4]、自适应控制[5]等。文献[6]提出了双环无抖积分滑模控制方法,大大简化了滑模控制器的设计方法,但由于引入了积分的环节,很容易造成误差积分饱和的问题。文献[7]针对直接跟踪期望位置姿态超调过大的问题,提出了双闭环终端滑模控制方法,外环经位姿反馈量获得虚拟控制量实现对位姿误差的镇定,内环跟踪虚拟控制率实现对速度误差的镇定。文献[8]针对参数摄动和海流干扰下AUV平面目标跟踪的问题,提出了模糊自适应轨迹跟踪控制器,仿真实验中可以看出模糊自适应算法仍会给控制系统带来误差。文献[9]采用状态反馈线性化方法对AUV数学模型进行线性化,降低其非线性程度。文献[10]潜航器以非线性耦合模型作为控制对象,构建基于精确反馈线性化的潜航器编队协调控制系统,由于采用协调控制器相对简单,整个控制系统的收敛速度较慢。文献[11]采用了边界层自适应终端滑模的控制方法来抑制滑模控制带来的系统抖振的问题。文献[12]针对在有界未知扰动下的欠驱动AUV水平面轨迹跟踪控制问题,设计了基于积分滑模的轨迹跟踪控制器,极大提高了控制器在有界干扰下的鲁棒性,但文中对未知干扰的抑制并未提出有效的解决方法。
综上分析可知AUV在复杂海洋环境下的精准三维轨迹控制仍存在诸多挑战,本文对全驱动AUV模型进行反馈线性化,考虑在定常海流以及未知环境的干扰下,对线性化后的模型设计自适应可变参滑模的控制器,并引入比例积分观测器,实现AUV在未知复杂环境中的精准无抖振三维轨迹跟踪控制。
1 AUV模型
图1中O-NED为北东坐标系即固定坐标系,B-xyz为船体坐标系即惯性坐标系。AUV的执行机构配置为:主推进器在AUV的艉部布置,实现AUV纵向速度控制;辅助推进器在AUV的两侧和顶部对称布置,实现AUV横向速度和垂向速度控制;垂直舵实现AUV艏向角控制;水平舵实现AUV纵倾角控制。AUV的空间运动具有全驱动的特性,空间运动坐标系如图1所示,并在船体坐标系下建立的数学模型可表示为:
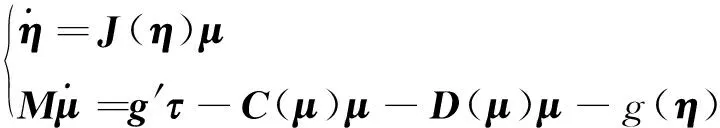
(1)
式中:η=[xyzθψ]T∈R5表示AUV在大地坐标系下的位姿向量;μ=[uvwqr]T∈R5表示AUV在船体坐标系下的速度向量;M是惯性矩阵,包括附加质量;J(η)是变换矩阵;C(μ)是向心力和科氏力矩阵,包括附加质量产生的向心力和科氏力;D(μ)是水动力阻力和升力力矩;g(η)是恢复力和力矩向量;τ=[τuτvτwτqτr]T∈R5是在船体坐标系下的控制器输入向量。g′∈R5×5是执行机构的参数矩阵。忽略高阶非线性水动力阻尼项和横摇运动对该AUV三维空间运动的影响,AUV的运动学和动力学数学模型以及模型参数见文献[10]。
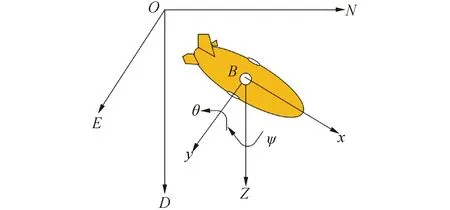
图1 AUV坐标系Fig.1 Reference frames of AUV
2 AUV控制器设计
2.1 AUV模型的反馈线性化
反馈线性化的主要思路是利用反馈的方法将非线性系统精确线性化或部分精确线性化,反馈线性化适应于大部分的非线性控制系统,若非线性系统的相对阶之和等于系统的阶数,就可以将非线性系统进行精确线性化。
令:
N(η,μ)=-C(μ)μ-D(μ)μ-g(η)
(2)
则式(1)为:
(3)
为了便于模型的反馈线性化,将式(3)写成为:
(4)
式中:
ξ=[xyzθψuvwqr]T,
取非线性系统的输出量为位姿向量,AUV非线性模型为:
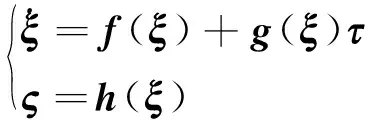
(5)
且h(ξ)=[xyzθψ]T,g(ξ)=M1g′。根据文献[13] Lie导数相关内容可知:
(6)
由此可得一阶Lie导数Lfh(ξ)、Lgh(ξ)为:
(7)
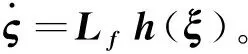
同理根据二阶Lie导数的定义,可知:
(8)
(9)
引理1[13]n阶仿射非线性系统精确线性化有解的充分必要条件是,当且仅当存在一个标量函数h(x),使得如下系统:
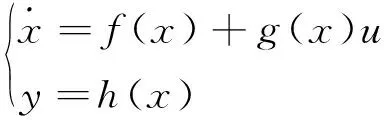
(10)
在x0∈U点的相对阶为n。
根据相对阶的定义可知,该模型的相对阶之和为:ρ1+ρ2+ρ3+ρ4+ρ5=10,其中ρ1=ρ2=ρ3=ρ4=ρ5=2,即相对阶的和等于系统的阶数10,由引理1得知,该模型可以进行精确反馈线性化,并且有解。选择坐标变化如下:
(11)
将式(7)代入得:
(12)
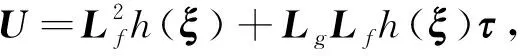
可得到AUV线性化数学模型为:
(13)
2.2 AUV轨迹跟踪控制器设计
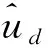

图2 AUV控制系统框图Fig.2 Block diagram of AUV control system
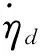
假设2海流干扰是定常有界的干扰,且外界环境中的未知干扰是有界周期性的。
设ηd为期望的运动轨迹,考虑定常海流扰动,海流大小为vbm/s,流向角为α,则z1d=ηd,z1e=z1-z1d,z2e=z2-z2d+vdis,海流扰动量在船体坐标系下对AUV速度的影响为:
(14)
式中:uc为海流扰动对AUV纵向速度的干扰量;vc为海流扰动对AUV横向速度的干扰量。根据文献[14]取滑模面为:
s=k1z1e+k2z2e
(15)
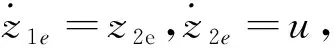
(16)
其中k1,k2>0,取指数趋近率为:

(17)
式中:k是等速项趋近系数(constant velocity approach coefficient),k>0;ε是指数项趋近系数(exponential approach coefficient),ε>0。将式(17)代入式(16),可得到控制量U,即:
U=(-kk1z1e-(kk2+k1)z2e-εsgn(s))/k2
(18)
通过仿真和查阅资料可知,使用这种趋近率得到的控制器可以实现系统的稳定和收敛,但是会带来持续性的周期抖振,不利于执行机构的平稳输出。指数项趋紧系数ε是造成抖振的主要因素,将ε设计成自适应可变参,可以消除滑模控制器的抖振。
令ε=k3‖s‖,其中‖s‖为设计滑模面的模值,ε与‖s‖成正比,当控制系统趋近滑模面,ε便无限趋近于零,从而实现无抖振的滑模控制。将ε代入式(18),可得自适应可变参的滑模控制律:
U=(-kk1z1e-(kk2+k1)z2e-
k3|s|sgn(s))/k2
(19)
AUV在实际的海洋环境中受到的扰动不仅有海流的扰动,还有除海流外其他的未知环境扰动。为了实现AUV的三维空间轨迹跟踪器在有界控制输入和外界未知扰动作用下的稳定性,将式(13)的AUV动力学反馈线性化的模型中加入有界未知干扰,得到:
(20)
式中:ud=[ud1ud2ud3ud4ud5]为有界的未知环境扰动。对应的AUV控制器为:
U=(-kk1z1e-(kk2+k1)z2e-
(21)
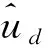
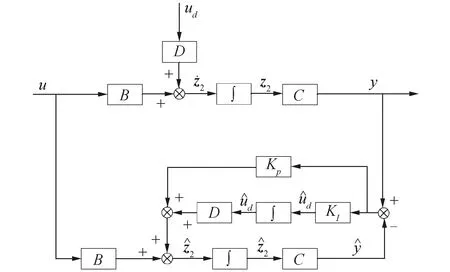
图3 观测器结构框图Fig.3 Structure block diagram of observer
图3中,B,C,D∈R5×5均是单位矩阵,KP、KI分别是比例系数和积分系数。针对未知扰动部分设计的控制律为:
(22)
2.3 稳定性分析
定理:满足假设1、2的全驱动AUV,在自适应可变参滑模控制律式(21)和未知扰动控制律式(22)的控制下,通过调整设计参数使跟踪误差渐进收敛到零值附近,保证系统是全局稳定的。
证明:选取Lyapunov函数为:
(23)
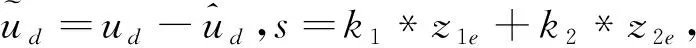
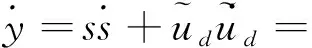
(24)
将式(22)代入式(24),得:
(25)
将式(25)分成2个部分进行稳定性分析,即:
(26)
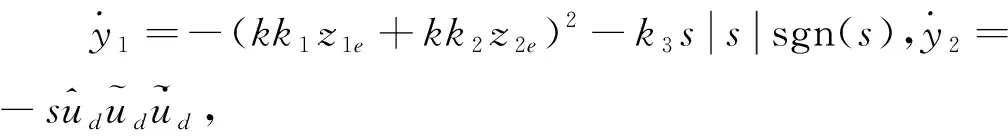
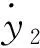
对于未知扰动观测器模型:
(27)
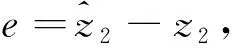
(28)
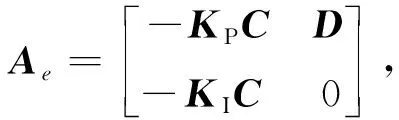
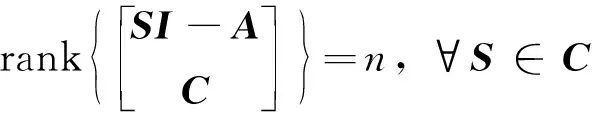
即:
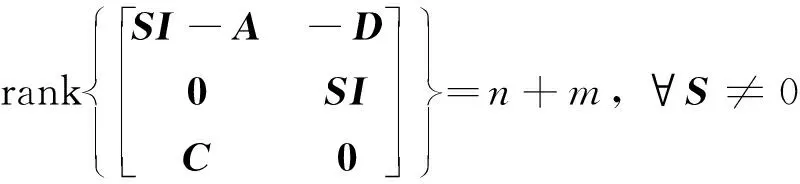

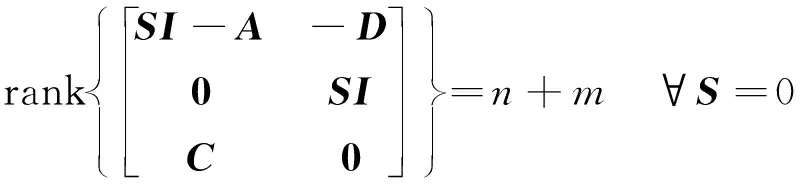
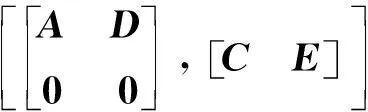
(29)
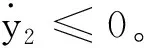
由式(23)可知定义的Lyapunov函数是正定的,同时Lyapunov函数的导数是负定的,故在控制输入式(21)的作用下,闭环系统渐近稳定,定理得证。
3 仿真实验与分析
3.1 仿真实验1:模型比对验证
首先针对非线性AUV模型设计本文的控制器(nonlinear adaptive sliding mode control,NASM),然后针对AUV反馈线性化模型设计本文的控制器(linear adaptive sliding mode control,LASM),最后设计相同的期望路径进行对比。不考虑海流以及环境的扰动,期望的运动轨迹如下:
(30)
AUV的初始位置y(0)为5 m,x(0)为65 m,深度为0 m,初始姿态θ(0)为0,艏向角ψ(0)为π/2,纵向速度u(0)为0.5 m/s,其他速度都初始化为0 m/s,控制器参数为k=1,k1=1,k2=1,k3=0.007,该条件下仿真结果如图4所示。
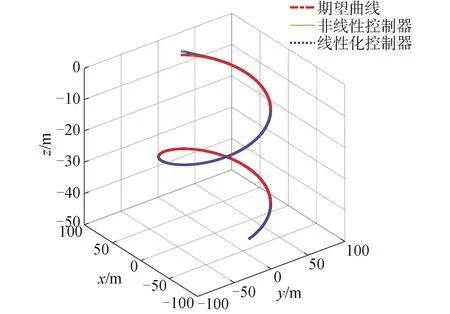
图4 AUV三维轨迹Fig.4 AUV trajectory
图4是AUV的三维运动轨迹图,可以看出2种控制器都能够在有限的时间内跟踪上期望的轨迹。因为是螺旋下潜的运动轨迹,所以AUV会在运动过程中产生横向漂移的运动现象,在横向速度的控制器作用下可以将实际的横向速度稳定在期望值附近。从图6可以看出使用NASM控制方法AUV的垂向速度w和纵倾角速度q会出现连续的周期性的抖振,而LASM能够实现稳定平滑的控制。通过仿真验证了非线性系统设计的控制器设计的缺陷,如收敛速度慢,抖振以及控制器设计复杂和控制参数繁多等问题;设计的可变参自适应线性滑模控制器能够快速对位姿和速度误差进行镇定,具有调节时间短和设计简单等优点。
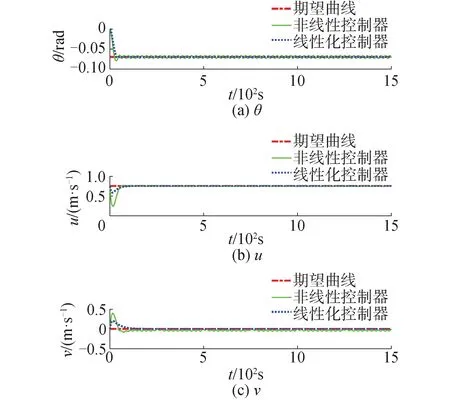
图5 AUV 姿态角和速度状态Fig.5 AUV attitude angle and velocity state

图6 AUV纵向速度和角速度Fig.6 AUV longitudinal velocity and angular velocity
3.2 仿真实验2:定常海流以及未知环境干扰下的AUV三维轨迹跟踪
针对定常海流和外界未知干扰下的AUV三维轨迹跟踪控制问题,使用基于自适应可变参滑模控制器(adaptive sliding mode control,ASM)和常规滑模控制器(sliding mode control,SM)以及常规反步法控制器(backstepping control, BS)进行仿真实验对比。考虑仿真的海流环境为海流大小为0.2 m/s,海流方向为30°,加入的未知环境干扰量为ud=[ud1ud2ud3ud4ud5]T,每个方向的干扰分布在[0,0.5]。AUV的期望运动轨迹如下:
(31)
(32)
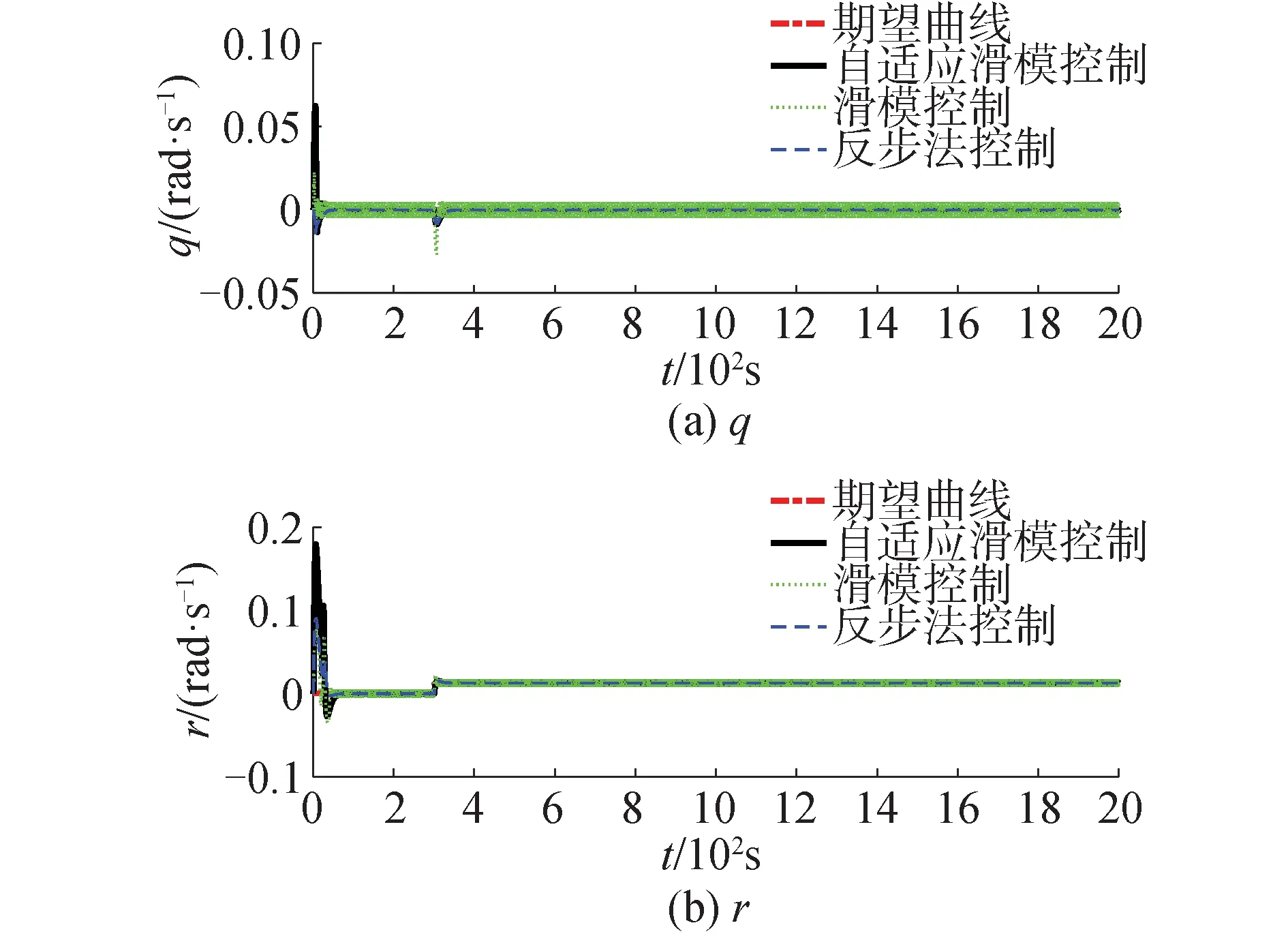
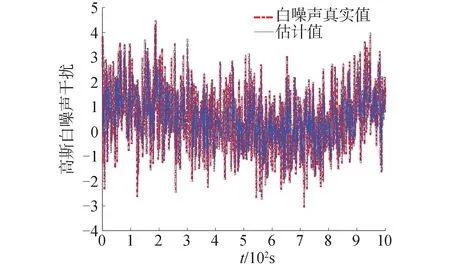
式中300 AUV的初始状态为:初始位置x(0)为10 m,y(0)为10 m,z(0)为-3 m,初始姿态θ(0)为0.18 rad,艏向角ψ(0)为π,纵向速度u(0) 0.5 m/s,其他速度都初始化为0 m/s,控制器参数为k=1,k1=0.4,k2=0.7,k3=0.017,比例积分观测器增益矩阵为: 仿真结果如图7~11所示。从图中可以看出3种控制方法都能实现期望的轨迹跟踪,但滑模控制器和自适应可变参滑模控制器的收敛速度快于反步控制器。从图8中可以看出在t=300时进行匀速螺旋下潜,下潜速度为0.112 m/s,纵倾角保持在-4°左右,3种控制器下的AUV能跟踪上期望的运动轨迹。 图7 未知干扰下的AUV三维轨迹Fig.7 Three-dimensional trajectory of AUV under unknown interference 图8 未知干扰下的AUV状态Fig.8 AUV status under unknown interference 图9 未知干扰下的AUV角速度状态Fig.9 AUV angular velocity state under unknown interference 此次仿真实现加入了海流以及环境的未知干扰,因此在初始时刻AUV的速度量控制会产生较大超调;并且从仿真图中可以看出,反步控制器下的AUV纵向速度、横向速度和纵倾角速度的超调量明显大于滑模控制器和自适应可变参滑模控制器下的速度超调量,但滑模控制器在系统稳定时会出现周期性抖振。速度超调量始终在控制器的调控范围内,在控制器的控制作用下这些速度量能够快速稳定到期望值处,且速度误差最终收敛到0。图10和11是未知环境连续可微干扰ud的仿真图,图12是使用文中观测器对高斯白噪声的观测。从仿真图中可看出本文设计的比例积分观测器能够快速、高效地完成对未知干扰的观测。 图12 高斯白噪声干扰的真实值与估计值Fig.12 True and estimated values of gaussian white noise interference 综合来说,设计的自适应可变参滑模控制器能够实现无抖的AUV三维轨迹运动控制,并且控制器具有快速镇定位置误差和速度误差的功能,能够实现未知扰动环境下的复杂期望轨迹的无抖振控制。 1)可以使用精确反馈线性化的方法将非线性、强耦合的全驱动AUV模型转化为精确线性化的模型。 2)可以使用比例积分观测器对复杂海洋环境中的有界未知干扰进行精准观测。 3)设计的自适应可变参滑模控制器能够有效抑制传统滑模控制器中的抖振问题。 4)仿真结果表明所设计的控制器误差收敛速度快,能够有效克服非线性系统为控制系统带来系统误差的问题,能较好地实现AUV在复杂海洋未知干扰环境下的三维时变轨迹的精准控制。 对于AUV的复杂系统,本文研究的是全驱动的AUV模型,欠驱动的AUV同样存在着强耦合、非线性等共性问题,更有着高阶速度量不能积分的问题,对于这些复杂的AUV模型进行精确反馈线性化或者部分线性化无疑是复杂、困难的。此外真实的海洋中AUV模型存在不确定性,本文采取的是未知有界的时变周期函数模拟海洋的未知干扰,后续研究将会考虑真实情况欠驱动AUV在存在不确定性和有界未知多变的海洋干扰下的轨迹精准控制。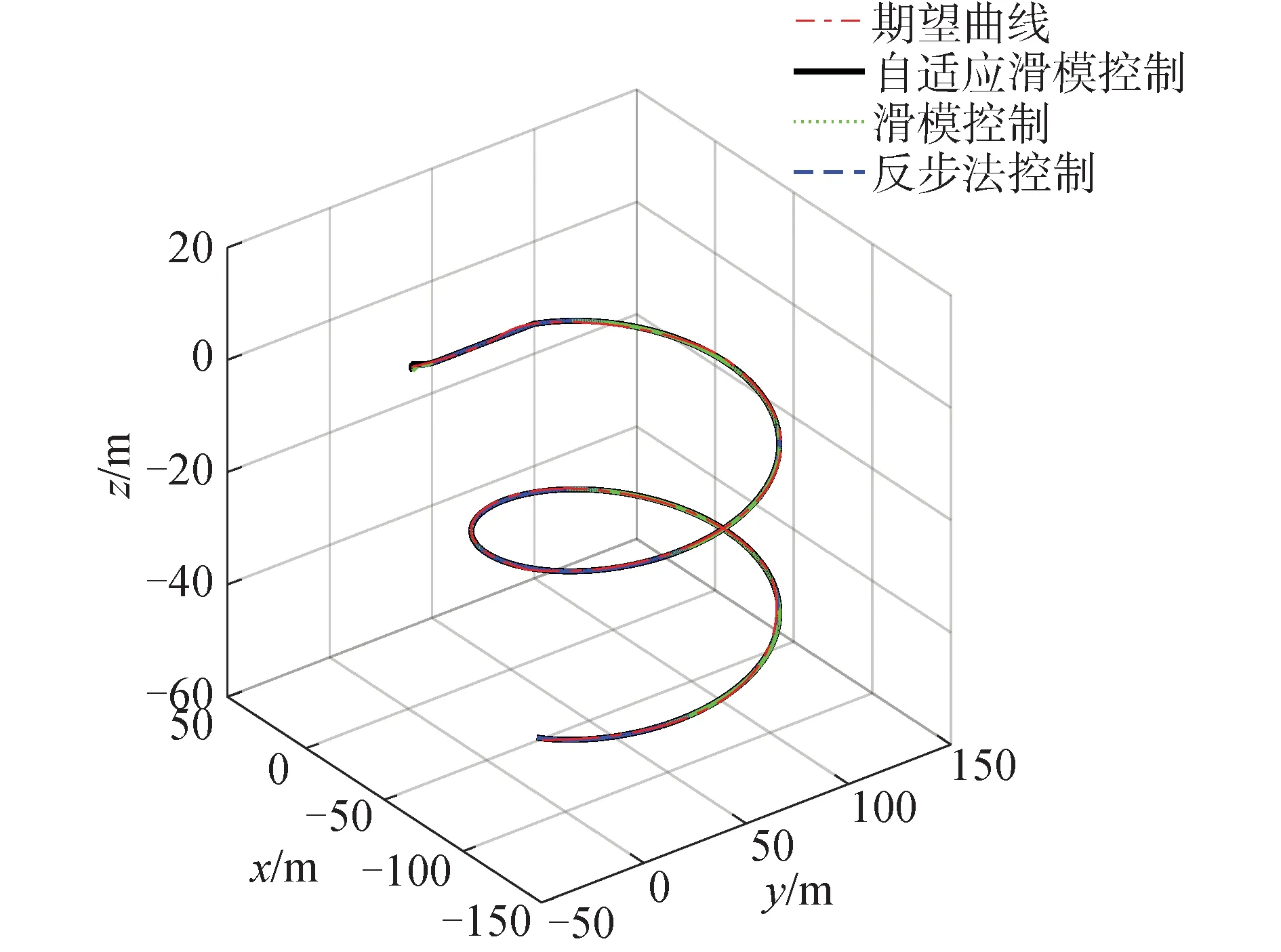

4 结论

