反哈密顿矩阵的特征值反问题
胡姗姗,李思思,罗佳杰
(湖北师范大学 数学与统计学院,湖北 黄石 435002)
0 引言
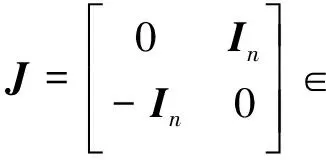
特征值反问题与矩阵特征值问题相反,需要由特征值和特征向量来确定矩阵的元素。特征值反问题被广泛应用于许多研究领域,如结构动力学[1~4],极点配置[5,6]等。关于矩阵的特征值反问题可以在文献[7]中找到。反哈密顿矩阵的特征值反问题有许多重要的应用,并有许多计算其特征值、不变子空间和舒尔形式的算法。本文利用广义奇异值分解研究反哈密顿矩阵的特征值反问题的可解性条件和通解表示。
本文主要解决以下两个问题:
HX=XΛ
(1)
对矩阵对进行广义奇异值分解,给出了最佳逼近问题有解H的充要条件。当集合SE非空时,证明了最佳逼近问题存在唯一解,并给出了唯一解的显示表达式。
1 特征值反问题
为了解决特征值反问题,给出下面的引理

引理2[9]令S1=diag(α1,…,αs)∈s×s,S2=diag(β1,….βs)∈s×s且满足g×s,则
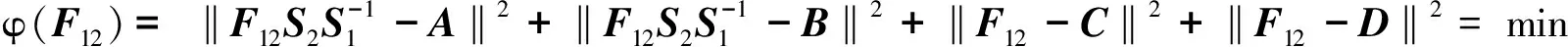
当且仅当
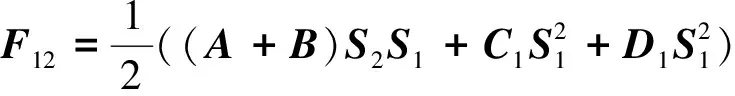
(2)
引理3 假设S1=diag(α1,…,αs)∈s×s,S2=diag(β1,…,βs)∈s×s且满足s×s,则
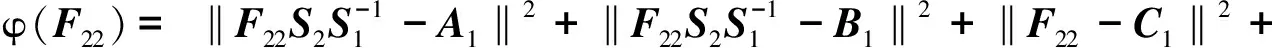

(3)
当且仅当
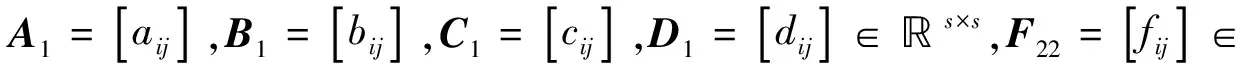
由于fij=-fji,容易得到
由上式的矩阵形式,可以得到结论。
假设H∈H2n×2n,由引理1,H可以表示为
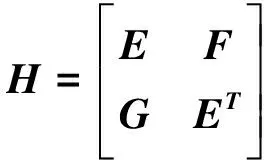
(4)
其中E,F,G∈n×n可以被确定。令αi=Re(λi),βi=Im(λi),yi=Re(xi),zi=Im(xi),i=1,3,…,2l-1.

(5)
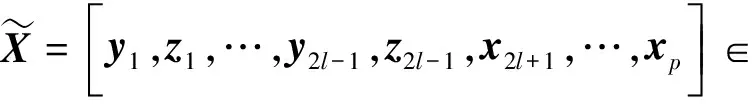
(6)
方程(1)可改写为
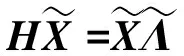
(7)
设矩阵
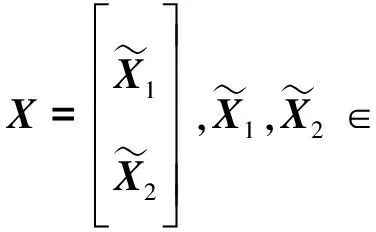
(8)
由(4)和(8),方程(7)可以写成

(9)
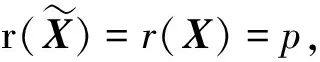
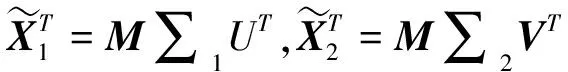
(10)
其中M∈p×p是非奇异矩阵,n×n
1>α1≥α2≥…≥αs>0,0<β1≤β2≤…≤βs<1,αi+βi=1(i=1,…,s),
令

(11)
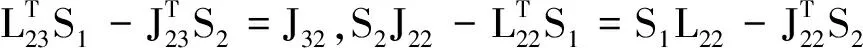
(12)
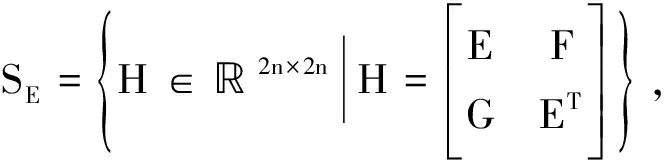
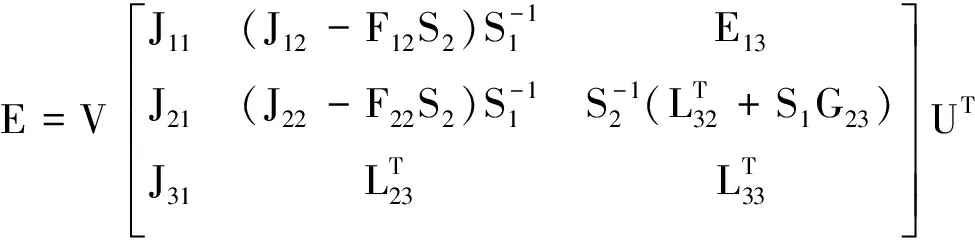
(13)
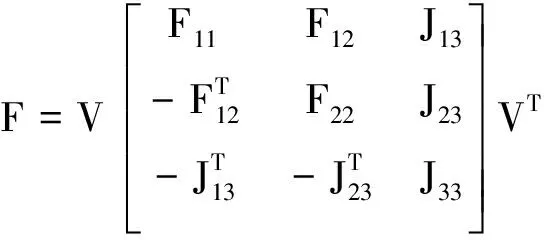
(14)

(15)
E13,F12,G23是任意矩阵,F11,F22,G33是任意反对称矩阵。
如果令
则有下面各式成立
E11=J11,E12S1+F12S2=J12,F13=J13,E21=J21,E22S1+F22S2=J22,F23=J23,
由上面各式之间的关系可得,可解条件(12)以及关系式(13)~(15)。
2 最佳逼近问题

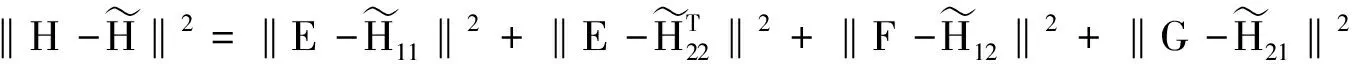
(16)
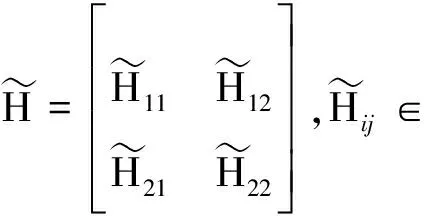
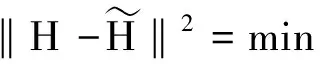
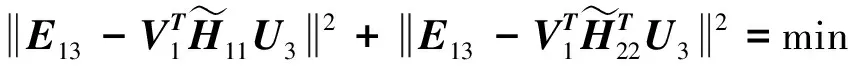
(17)

(18)
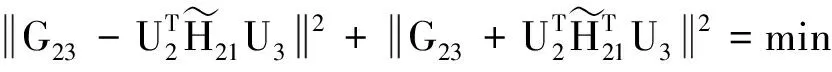
(19)

(20)
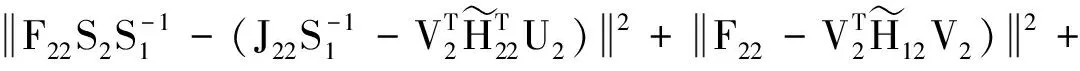
(21)

(22)
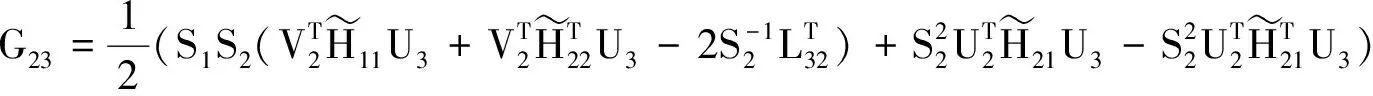
(23)
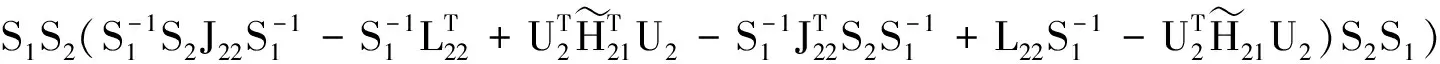
(24)
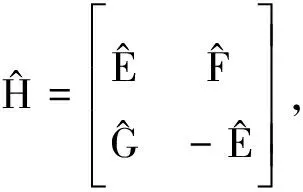
其中F12,G23,F22分别由式(22)(23)(24)表示。

