基于自抗扰控制器的变桨距控制系统

杨 亚，李玉爽，徐 杰

(1.芜湖职业技术学院 智能制造学院， 安徽 芜湖 241006; 2.江苏省电力设计院，江苏 南京 211102)

近年来，能源问题日益突出，生态环境不断恶化，人们需要用一种清洁、可再生的新能源来取代传统的化石能源，因而风能因具备可持续、绿色以及环保等优点，近些年在全球范围内被大力发展，具有很好的应用价值[1]。

本文是基于风力发电系统中发电机的变桨距系统，对于存在的不确定性、非线性、建模难度高以及多干扰等问题，通过对其内部结构与性能进行优化，开发设计出相应的控制系统。将系统的内部扰动(参数摄动、模型的不确定性)以及外部扰动一同视为系统的总干扰，利用扩张状态观测器的作用，对于系统中出现的扰动以及状态变化进行观测，并将其消除。用仿真分析验证其有效性。然而，由于变桨距系统自身是一种时滞系统，时延的存在会降低系统稳定性，因此本文在传统的ADRC的基础上将史密斯预估技术引入到自抗扰控制器(ADRC)设计中，设计了一种输出预估自抗扰控制器，在一定程度上提高了系统的控制性能。本文主要对以下几个方面进行了研究：第1部分建立风机气动系统模型、永磁同步发电机模型、变桨距系统模型；第2部分建立基于输出预估自抗扰控制器的变桨距控制系统；第3部分得出仿真结果并进行分析。

1 风力发电系统的建模及动态特性

1.1 风机气动系统模型

由贝兹(Betz)理论可知，风叶轮吸收的风能经转换变为机械能，具体可表示如下[2]:

(1)

风轮从风能吸收的气动转矩为

(2)

其中：R为风轮半径，m；Cp(λ,β)为功率利用系数；ρ为空气密度，kg/m3；λ为叶尖速比；v为风速， m/s；β为桨距角，(°)。此时，叶尖速比λ具体描述如下[3]：

(3)

其中：n为风机转速，r/min；ω为风机角速度。

功率系数Cp是λ和β的非线性函数，其大小主要取决于叶片的类型和运行条件[4]:

(4)

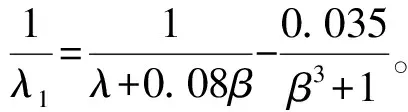
为了研究风能利用系数Cp的动态特性，本文基于MATLAB/Simulink得到了Cp二维曲线图，如图1所示。由仿真曲线可以发现，每一个桨距角都有一个可以使功率利用系数达到最大值的λ参数，此时，叶尖速比参数就作为系统的最佳叶尖速比。不仅如此，通过以上内容可以发现，随着桨距角的增大，风能利用系数越来越小，当桨距角β=0且λ=8时功率利用系数最大(Cp)。由式(3)可知，叶尖速比λ是风机的角速度ω与风速v的函数，因此，若要使系统的时钟处于最佳叶尖速比的状态，就需要用调节电机的风速及转速的方式来实现，以得到最佳功率输出。

1.2 永磁同步发电机数学模型

在d-q同步旋转坐标系下，永磁同步发电机数学模型可描述如下[4]:

(5)

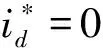
(6)

直驱式风电机组传动系统的数学模型可以描述为[5-9]

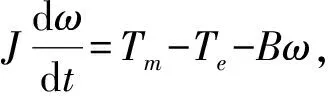
(7)

其中：Tm为风机驱动转矩，N·m；B为黏性摩擦系数，N·m/(rad/s)；J为转动惯量，kg·m2。

1.3 变桨距执行机构数学模型

在实际应用中，受到风机机械旋转部件转速的限制、电力电子器件功率等因素的影响，风力发电系统不能为了追求最大功率而无限制地增加风机的旋转速度。为了保证设备的可靠运行，当发电机达到额定转速以上时，就需要采取相应的控制措施将输出功率维持在额定功率，通常会利用变桨距控制技术来实现。变桨距执行机构通常由伺服驱动液压装置实现，其主要作用是根据变桨控制器给定的桨距角信号快速响应实时调节叶片桨距角。由文献[5]可知，可以简化为变桨距执行机构，等同于一阶惯性延时环节：

(8)

其中:βref为参考桨距角，(°)；τ为时间常数，s。

2 控制策略

2.1 时延系统预估自抗扰控制器(PADRC)设计

Smith预估器被广泛应用于时滞系统的补偿控制系统中，在补偿装置的作用下，把函数中纯滞后的部分和其他内容分开，同时对控制对象的纯时滞环节进行补偿处理。设时滞系统传递函数为

G(s)=Gr(s)e-τs,

(9)

其中，Gr(s)为控制目标处于非时滞时的传递函数，G(s)为时滞系统控制对象的传递函数，τ为控制目标的时滞因子。此外，常用的史密斯预估器结构框图如图2所示。

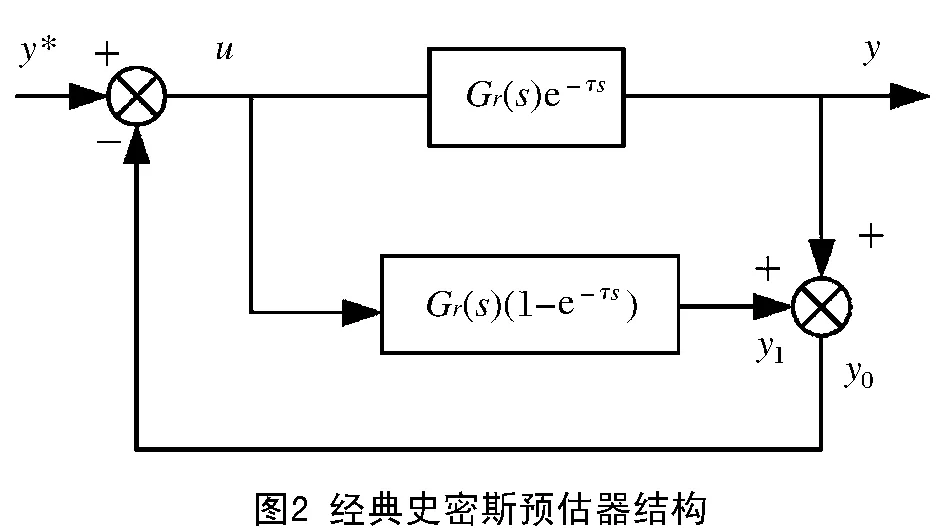
基于史密斯预估器的控制思想，为消除时延环节的影响，引入辅助函数y0，则可得

y0=y+y1

=Gr(s)e-τsu+Gr(s)(1-e-τs)u

=Gr(s)u。

(10)

当时延常数比较小时，式(9)可等效为

=eτsGr(s)e-τsu≈(1+τs)y，

(11)

式(11)表明辅助函数y0是由系统输出y和它的微分叠加而成，因此本文的预估自抗扰控制器设计思路为：为了消除系统输入输出的不匹配，首先通过引入预测函数y0使其与u保持同步，消除时延环节，然后再基于函数y0设计自抗扰控制器。这样既可以消除时延的影响，又能保证系统具备良好的瞬态响应和鲁棒性[10]。

预估自抗扰控制器(PADRC)可设计为

(12)

其中：z1为y0的估计值，z2为系统总扰动的估计值，b0为控制增益，u为控制输入，p为扩张状态观测器期望极点，kp为比例增益。

2.2 基于PADRC变桨距控制系统的设计

额定转速以上变桨距控制系统的主要目标是保证系统运行在额定功率附近，即实现系统的恒功率输出。设额定转速以上运行时，A点为系统恒功率输出点，对应额定功率为PN，额定转矩为TN,额定转速为ωN，参考桨距角为βN。若TN=PN/ωN，对则Tm在A点进行泰勒展开式：

Tm≈TN+α△ω+ξ△β+γ△v,

(13)

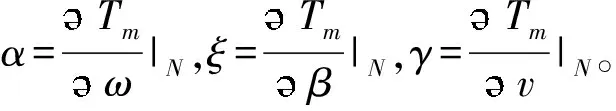
将式(7)代入式(13)可得

(14)

由桨距角动态特性可得

(15)

令b=ξ△β+γ△v-T△e为系统的总扰动，于是基于式(14)和(15),设计预估自抗扰控制器：

(16)

其中：kp为比例增益；p为扩张状态观测器极点；z1、z2分别是y0和系统总扰动的估算值，能够有效识别总干扰。图3为变桨距系统输出预估自抗扰控制原理图。

3 系统仿真及分析

本文采用MATLAB中Simulink的有效性分析方式，对所设计的自抗扰控制器进行了研究分析，分别进行了阵风与随机风2种风速的仿真。在仿真中用到的风电机组的参数如表1和表2所示。

表1 风力发电机组的主要参数

表2 风机系统的主要参数

自然风通常由基本风、随机风、渐变风、阵风组成。本文主要研究了阵风和随机风下系统的动态特性。

3.1 风速仿真

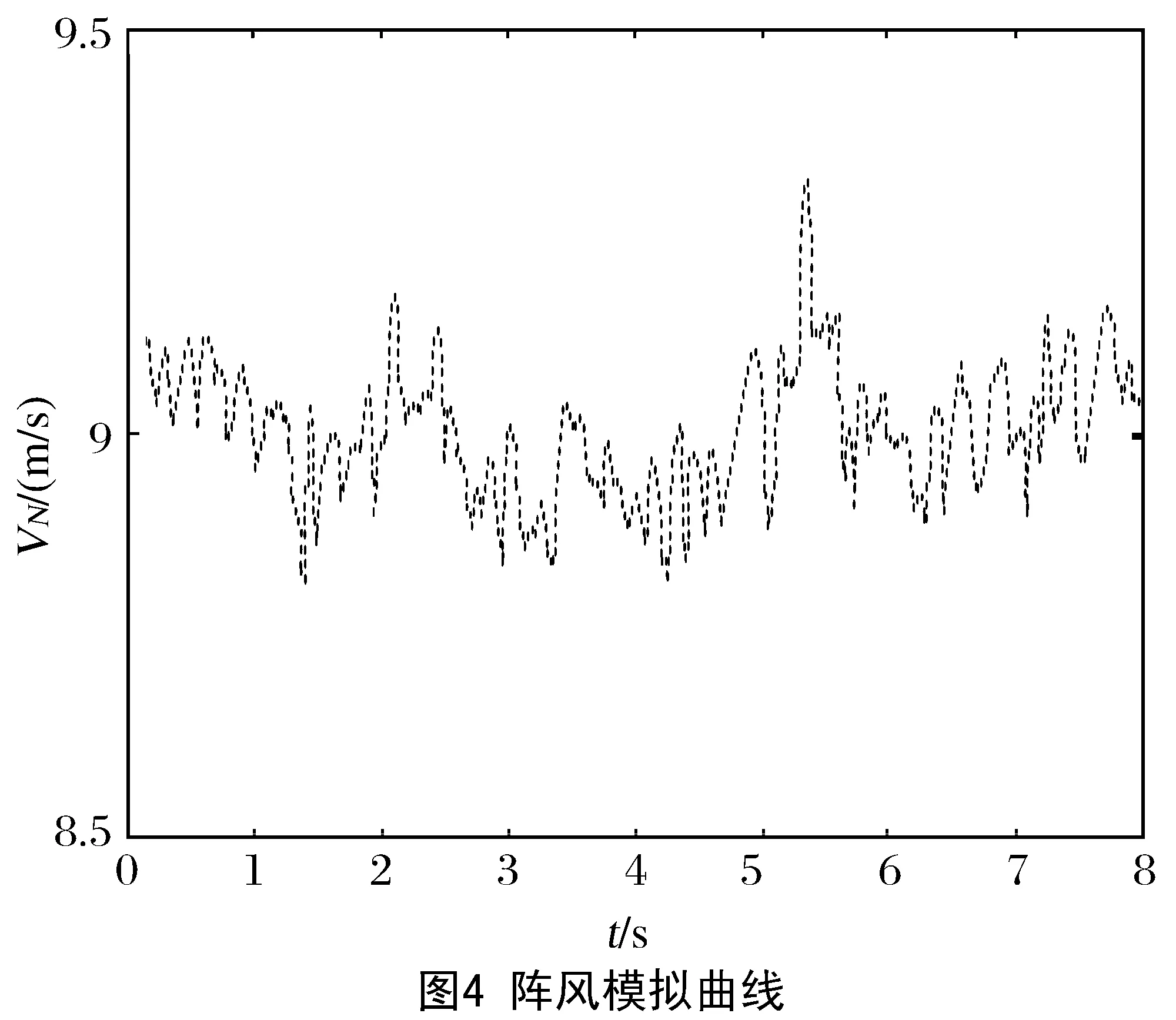
情形 1:阵风仿真

阵风描述了风速突然变化的特性，其数学模型可表示为

(17)

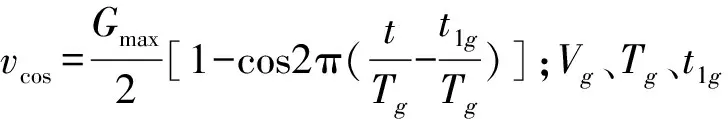
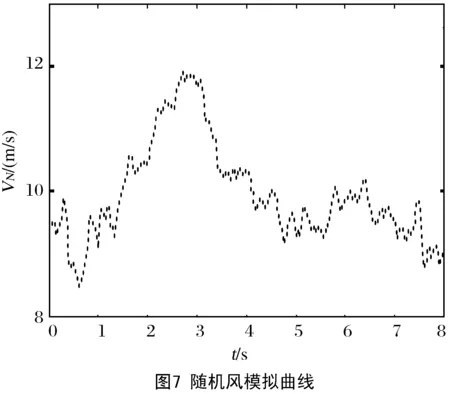
情形2: 随机风仿真

随机风描述了风速随机变化的特性，其数学模型为

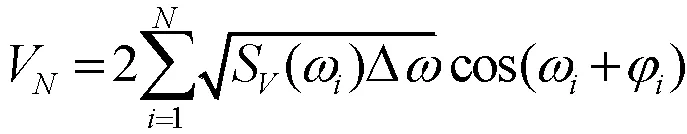
(18)

式中：ωi=(1-1/2)△ω, 是在区间0～2π上具有均匀概率密度的随机变量;SV(ωi)为谱密度函数。于是有

(19)

其中：φi为(0～2π)，为处于均匀分布状态的随机变量；u为风速的均值；F为扰动区间；KN为地表粗糙系数，其中N为曼宁粗糙系数。设定N=50，F=2 000，KN=0.004。

3.2 仿真结果分析

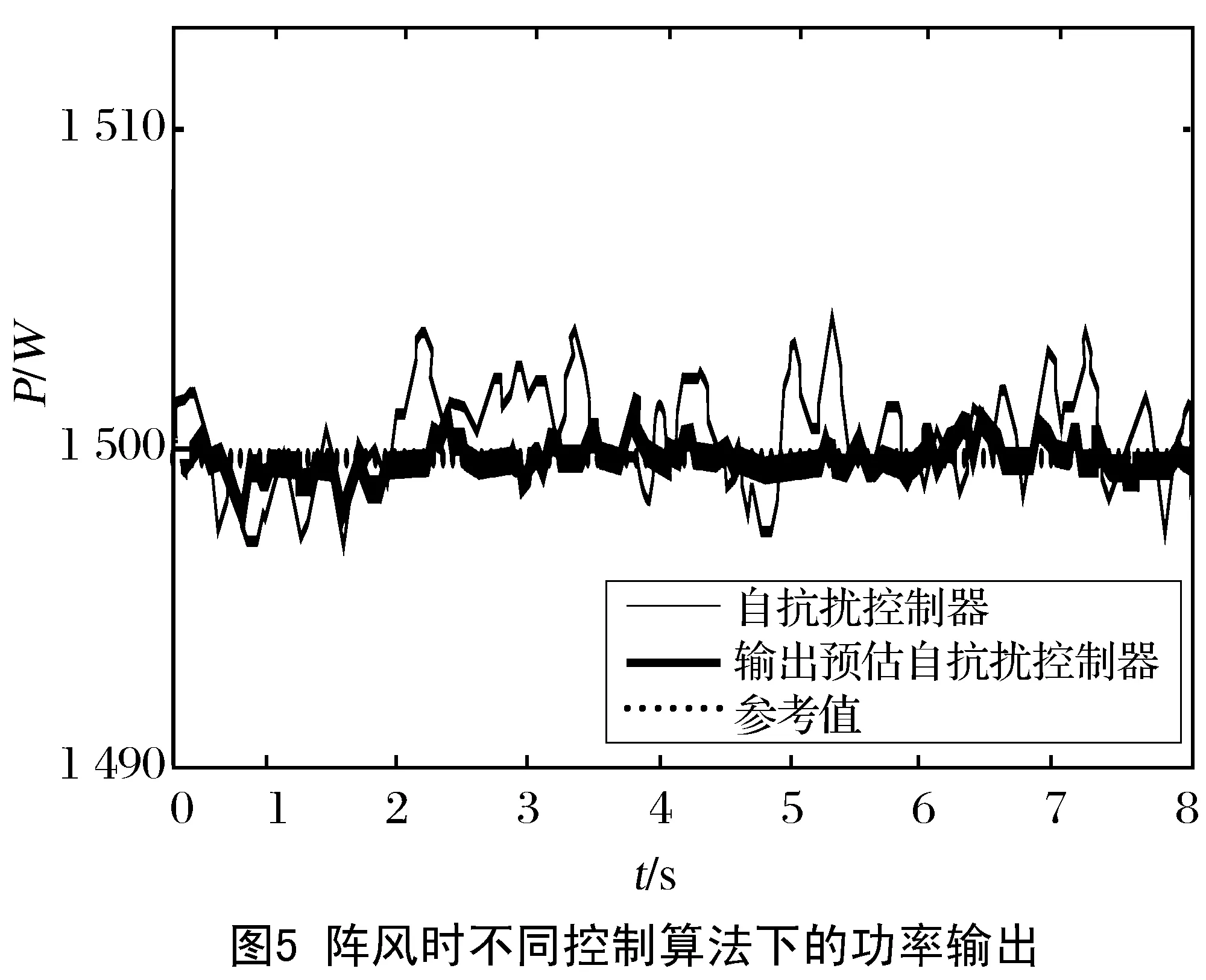
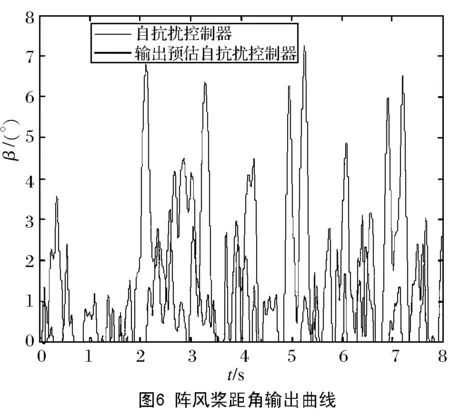
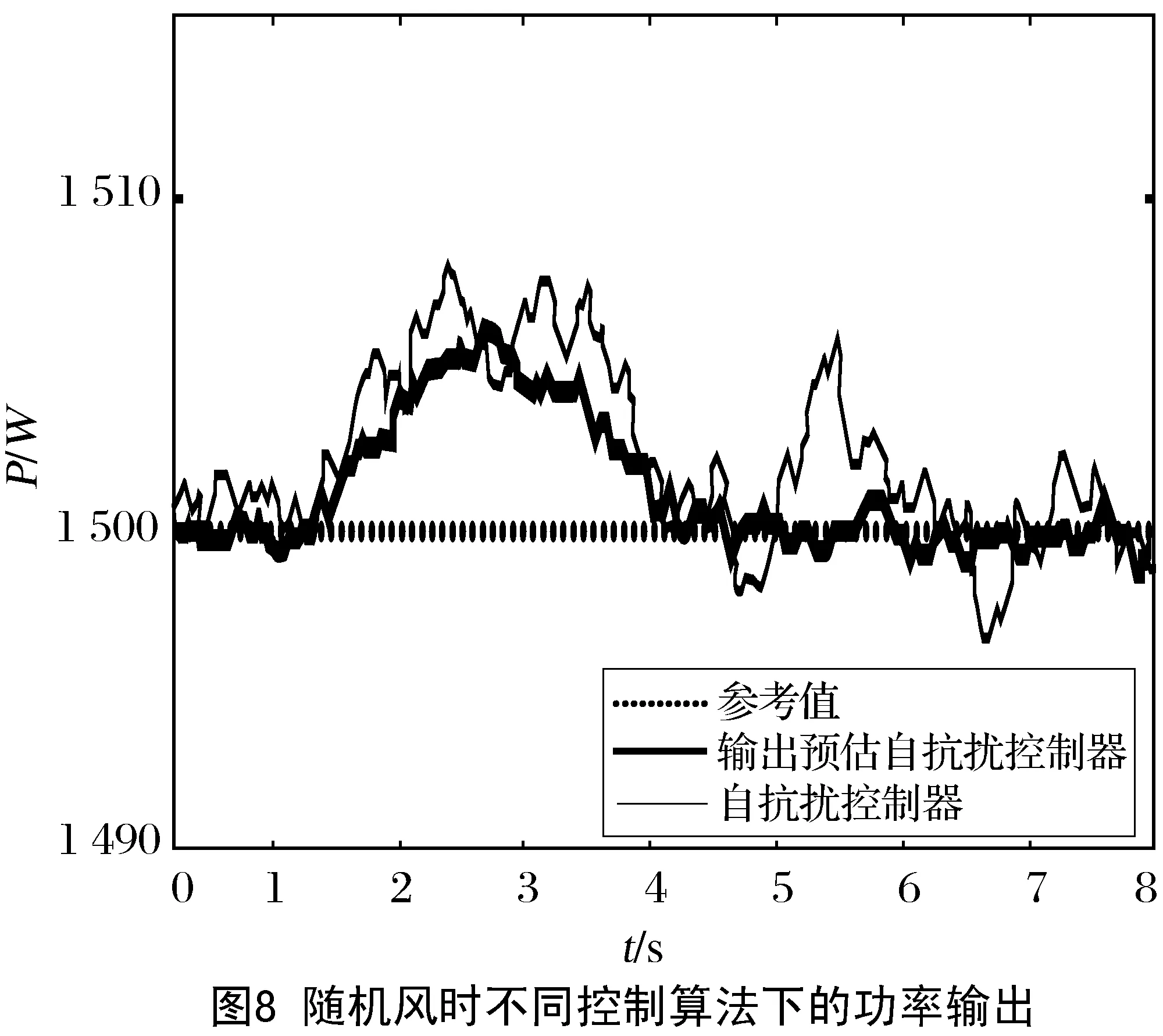
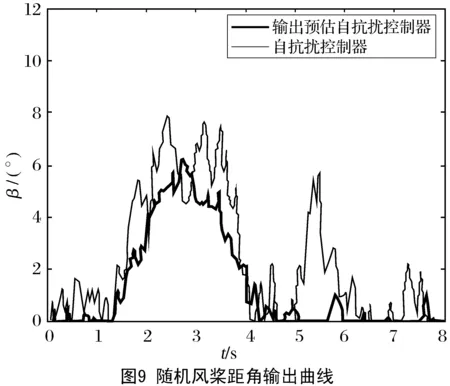
图4至图9分别给出了阵风和随机风下的2种不同控制策略的仿真曲线图。图5和图8分别给出了ADRC和PADRC两种控制算法下系统的功率输出曲线。由图5阵风仿真结果可以看出，与传统的ADRC算法相比，基于史密斯预估技术的PADRC能更好地保证系统输出功率维持在额定功率附近，PADRC的控制更稳定。图8表明，当风速突然变化时，PADRC能更快速响应外界风速的变化及时调整桨距角，从而使系统功率输出保持恒定。图6和图9分别给出了两种风速下系统桨距角的变化状态，采用PADRC控制的桨距系统桨距变化更稳定，控制效果更好。这是由于PADRC能快速消除系统内、外部时延的影响，使系统反馈输入更及时、更准确，从而大大提高了闭环系统的稳定性。

通过上述仿真分析可知，本文提出的PADRC控制算法相比经典的ADRC控制算法具有更高的稳定性、控制精度及更快的响应速度。

4 结论

变桨距控制技术被广泛地应用于风力发电系统的最大功率跟踪控制方面。本文分析了风力发电系统的具体特性，并建立了变桨控制系统的数学模型。针对额定风速以上的变桨控制，提出了一种基于自抗扰变桨控制技术的最大功率跟踪控制策略；考虑到变桨系统是一个时滞系统，基于史密斯预估器设计了一种具有更高性能的输出预估自抗扰控制变桨技术，并利用MATLAB中的Simulink进行了仿真分析，最后验证了其有效性。