基于事件触发机制的机械臂固定时间跟踪控制
贺芙蓉,操德文,2*,吴 健,2
(1.安庆师范大学 计算机与信息学院,安徽 安庆 246133;2.安庆师范大学 智能感知与计算安徽省高校重点实验室,安徽 安庆 246133)
近年来,由于实际应用中对节省系统资源的需要,基于事件触发机制的控制方法成为研究热点之一[1-8]。Song 等[3]提出了一个基于事件触发机制的自适应固定时间控制方案,来研究无人车系统的轨迹跟踪问题,在保证闭环系统固定时间稳定性的同时,减少控制器往执行器发送控制信号的次数。研究表明,相较于周期性地发送控制信号的时间触发机制,事件触发机制只有在满足触发条件时才通过网络传输数据,从而大大节省了系统的通讯资源。
有限时间控制的效果受到系统初始状态的约束,而由其发展而来的固定时间控制解决了这一问题,因而受到学者的广泛关注,并取得了许多成果[9-15]。从研究可知,固定时间的控制性能与被控系统的初始状态无关,只与系统控制参数选取有关,因而广泛应用于各种动力系统[16-18]。安思宇等[16]提出了一个基于Lyapunov稳定性理论的反推控制策略,解决了单链路机械臂的固定时间跟踪控制问题。
虽然文献[16]中采取了固定时间控制策略来解决系统跟踪问题,但是由于其选择了周期性时间触发机制,所以导致控制器向执行器发送了许多不必要的更新信号,从而出现了严重的资源浪费问题。为了节省系统通讯资源,减小系统压力,本文针对单链路机械臂系统,研究基于事件触发机制的固定时间跟踪控制问题。 本文的主要工作如下:1) 研究一种结合反推法和Lyapunov函数的固定时间控制方法;2) 通过事件触发机制来优化网络和通信资源占用问题, 同时为了避免出现传统反推控制中存在的“计算爆炸”问题, 引入带有命令滤波器的新型控制方法;3) 此外,本文采用固定时间控制方案,在闭环系统内的所有信号有界的情况下,使得系统输出信号能够追踪上期望信号,且收敛时间与系统初始状态无关,跟踪误差收敛到平衡点附近的一个小邻域内。
1 问题描述及预备知识
1.1 系统模型
考虑如下形式的单链路机械臂系统模型:

(1)
其中,b(t)表示机械臂的角度,m和l分别表示连杆的质量和长度,g是重力加速度,M是瞬时惯性,u(t)是输入扭矩,y(t)是系统的输出信号。
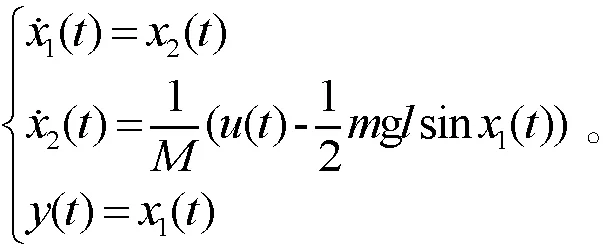
(2)
控制目标是针对模型(1)设计的一种基于事件触发的固定时间跟踪控制方法,满足:
1)系统输出y(t)在固定时间内跟踪上参考信号yg(t);
2)其跟踪误差在预定义的固定时间内收敛到零附近的任意小邻域内。
针对单链路机械臂模型(1),文献[16]提出的反推控制方法,解决了固定时间内机械臂系统的跟踪问题,使得系统输出信号可以在固定时间内跟踪上期望信号,但是其采用的时间触发机制大大占用了系统通信资源。针对这一问题,本文设计控制器时采用基于相对阈值的事件触发机制,降低网络和通信资源占用率,减小系统传输压力,更贴合实际应用情景;同时为了避免传统反推法中对虚拟控制器重复微分而产生的“计算爆炸”问题, 本文使用带有命令滤波器的新型控制方法。
1.2 重要引理和假设
为了实现上述控制目标,针对模型(1)作如下假设:



(3)


(4)


(5)
引理4[14]考虑下面非线性系统模型:
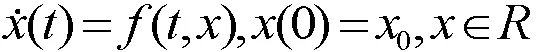
(6)
其中,x表示系统状态变量,f(·)为光滑连续的非线性函数。假设存在正定函数V(x),且其一阶导数形式可表示为

(7)
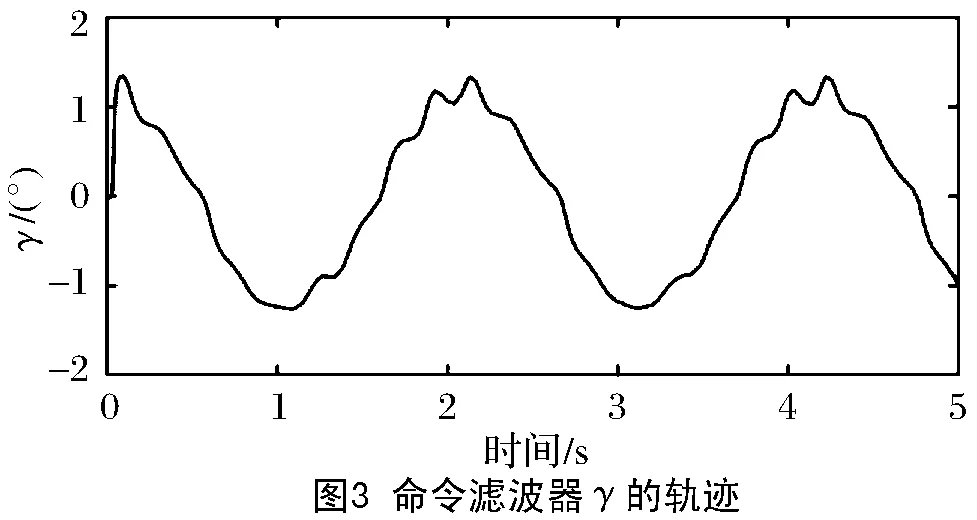
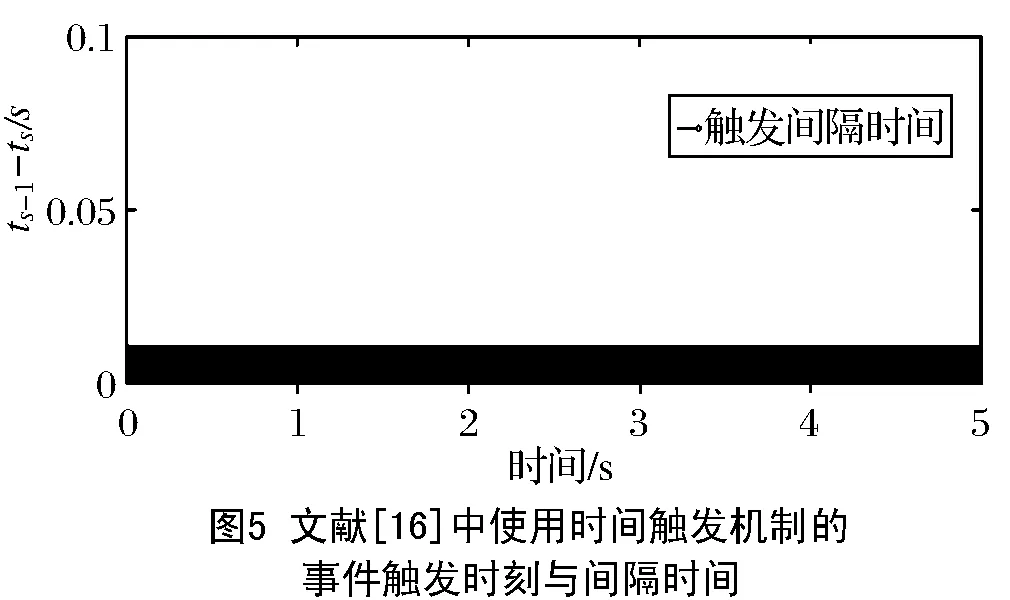
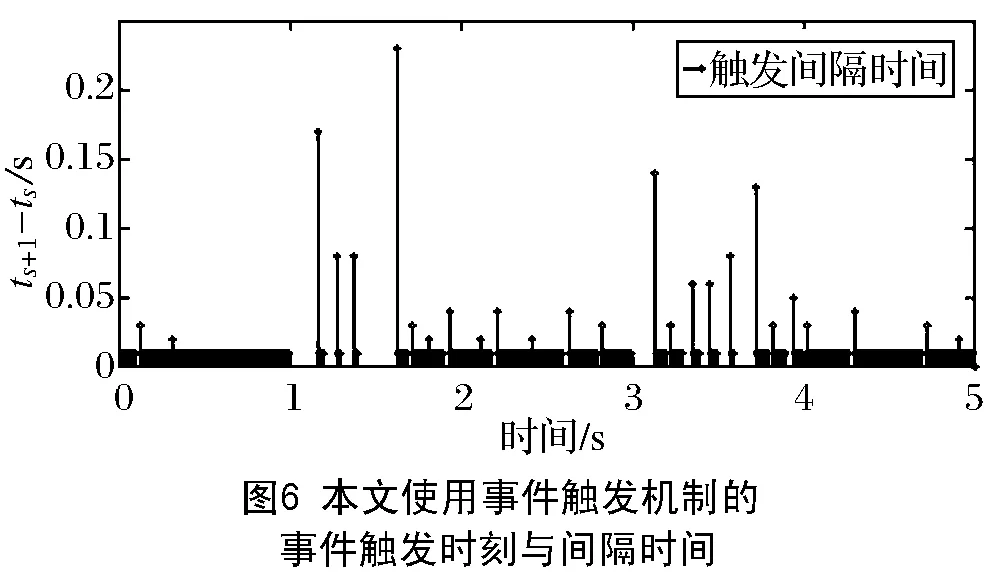
则模型(6)可以在固定时间内达到稳定状态,且系统跟踪误差收敛于平衡点附近的一个任意小邻域内,其中μ1,μ2∈R+,a0>1,0 (8) 为了便于讨论,以下推导过程省略时间变量t。 本节结合滤波器和固定时间稳定性理论,采用反推法,提出一种针对单链路机械臂的事件触发跟踪控制方案。首先将跟踪误差定义为 z1=y-yg, (9) 引入如下坐标变换: z2=x2-γ, (10) 其中γ满足方程(11)。 针对模型(2),下面给出具体的控制器设计过程: 第一步:为了克服传统反推控制方法存在的复杂性问题,将虚拟控制器通过如下二阶滤波器表示: (11) 其中:虚拟控制器α1是滤波器的输入,其具体表达式后面会给出;γ是滤波器的输出。定义滤波器误差为 ε=γ-α1。 (12) 结合公式(2)和公式(9),对z1求导,可得 (13) 再由公式(10)和公式(13),可得 (14) 构造第一个子系统的Lyapunov函数: (15) 结合公式(12)和公式(14),对V1求一阶导数,可得 (16) 设计虚拟控制器α1如下: , (17) , (18) (19) 其中:σ10∈R+为待设计参数,且满足σ10→0;系数c1,c2由下面的式子计算: (20) 根据引理1和公式(17),公式(16)中的z1α1可表示为 (21) 将公式(18)和公式(21)代入公式(16),整理后得 (22) 情形1:当|z1|≥σ10>0时, (23) 情形2:当|z1|≤σ10时, (24) 第二步:结合公式(10)和模型(2),得z2的时间导数为 (25) 考虑以下Lyapunov函数: (26) 计算得出V2的导数为 (27) 基于公式(27),设计控制器如下: (28) (29) 其中,S21∈R+,S22∈R+为待设计参数。 (30) (31) 其中,ω(t)=α2(t)-u(t),β0∈(0,1),β1∈(0,∞)为待设计参数。 因此,在区间[ts,ts+1)内,由于公式(30)和公式(31),控制器α2满足 α2=(1+K0β0)u+K1β1。 (32) 其中,K0(t)和K1(t)为时变常数,并且满足|K0(t)|≤1,|K1(t)|≤1。 因此,由公式(32)式可得 (33) (34) 由控制器公式(28)可得z2α2≤0。又因|K0(t)|≤1和|K1(t)|≤1,可以得到 (35) (36) 结合引理1、公式(28)和公式(35),采取类似于公式(21)中的分析,可以得到 。 (37) (38) (39) (40) 其中σ=σ1+σ2。 令q1=min(S11,S21),q2=min(S12,S22),根据引理2 和引理3,可以得到 (41) (42) 将公式(41)和公式(42)代入公式(40)中,可得 (43) (44) 根据引理4,其收敛时间即为 (45) 定理1:针对给定的单链路机械臂系统模型(1),在满足假设1后,采用事件触发控制策略公式(30)、(31),命令滤波器公式(11)以及虚拟控制器公式(17)和(28),并选取合适的设计参数,则闭环系统模型(1)在固定时间内能达到稳定状态,系统中所有信号都是有界的,并且其跟踪误差收敛于平衡点邻近的一个任意小的区域内。 本节使用MATLAB进行仿真实验来验证本文中提出的控制策略的可行性和有效性。 机械臂系统中的控制参数选取为M=1,m=1,g=9.8 m/s2,l=1。系统的初始状态为x1(0)=0.02,x2(0)=0.1。系统参考信号为yg=0.4×sin(3t)。事件触发控制策略里的参数设置为β0=0.8,β1=0.5。命令滤波器中的参数设计为μ1.1=10,μ1.2=50,μ1.3=10,μ1.4=8,v1.1=1,v1.2=5,v1.3=8,v1.4=1。 虚拟控制器α1、α2中的参数设计为σ1=1,σ2=1,S11=60,S12=60,S21=10,S22=10。 仿真结果如图1~图6所示。图1展示了系统输出信号y和预期跟踪信号yg的轨迹,可以看出,本文设计的固定时间事件触发控制策略可确保系统具有良好的跟踪性能。图2和图3分别展示了系统跟踪误差z1和命令滤波输出信号γ的轨迹。图4展示了控制器α2经过事件触发机制后产生的系统实际控制输入信号u。且由图2~图4不难看出,系统的跟踪误差z1、控制器控制信号u以及命令滤波器γ的输出都是有界的。图5~图6分别给出了文献[16]中使用时间触发机制和本文采用事件触发机制的系统事件触发时刻和触发时间间隔结果。从图5、图6中可以看出,文献[16]中采用的时间触发机制严格遵循固定时间间隔触发,而本文使用的事件触发机制使得触发间隔时间更长,减轻了系统的通信负担。 表1 文献[16]方法与本文方法性能对比 本文针对单链路机械臂系统,提出了一种基于事件触发机制的新型固定时间控制策略,确保系统在固定时间内能够跟踪上预期参考信号,并且收敛时间与机械臂初始状态无关,跟踪误差能够收敛到平衡点邻近的任意小的区域内。通过引入事件触发机制,降低了系统中传输控制信号的频率,很大程度上节约了系统的网络和通信资源。同时,利用命令滤波器解决了传统反推设计方法中存在的“计算爆炸”问题,大大降低了计算量。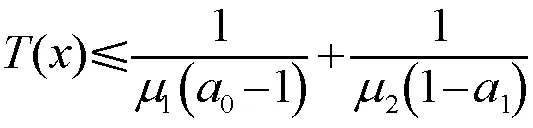
2 主要结果
2.1 事件触发控制器设计


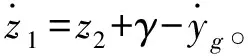


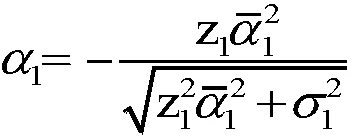
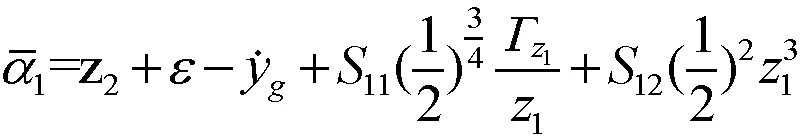









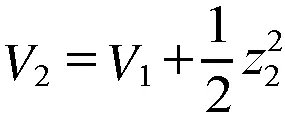
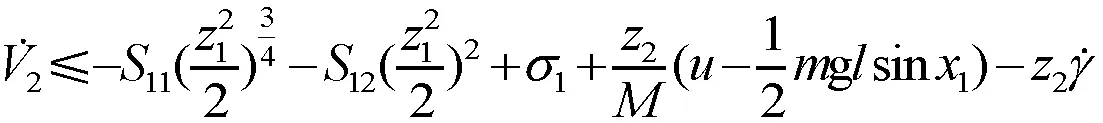
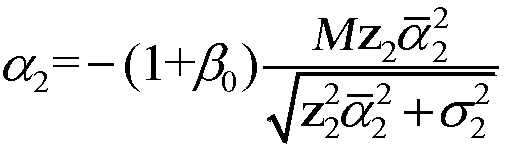
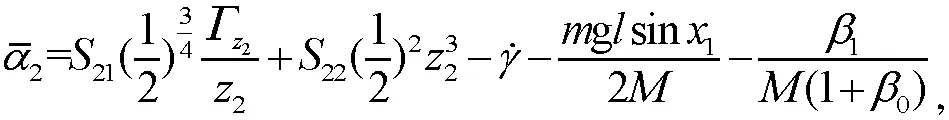















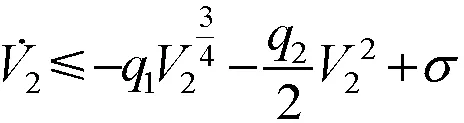
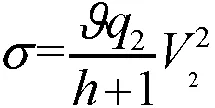


2.2 稳定性分析
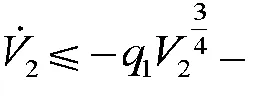
3 仿真与验证





4 结论

