基于隐式扩散的直接力格式浸没边界格子Boltzmann 方法1)

佟 莹 * 夏 健 * 陈 龙 *, 薛浩天 *

* (南京航空航天大学航空学院非定常空气动力学与流动控制工业和信息化部重点实验室,南京 210016)

引言

浸没边界(immersed boundary,IB)方法作为一种通用的数学框架和方法论在动边界绕流问题中广泛应用[1-4].与常规贴体网格方法相比,针对复杂外形几何体经历大变形的流固耦合动力学问题,IB 方法在计算效率和适应性等方面具备显著优势.主要原因有两个:第一,IB 方法采用两套彼此独立的网格分别离散流体域和浸没边界,从而避免了繁琐复杂的网格生成和再生过程;第二,作为一种数值格式,IB 方法通过向流体动量方程中添加体力项表征界面边界,无需对流动求解器代码进行过多修改,边界条件施加简单.

近年来,基于介观格子Boltzmann 模型(lattice Boltzmann,LB)发展流动求解器的计算流体力学方法(computational fluid dynamics,CFD)被使用处理各类复杂流动问题[5-10].相比于传统CFD 方法数值求解宏观守恒方程,LB 模型通过介观流体微团的碰撞和迁移描述流体动力学演化过程,控制方程格式更加简单、易于编程、边界处理方式简洁高效、并行特性更好.基于使用笛卡尔网格的共同特征,研究者试图将LB 与IB 集成为一种灵活处理复杂边界问题的CFD 方法.2004 年,Feng 和Michaelides[11]将罚IB 模型与LB 模型耦合,首次提出IB-LB 模型,并将其应用于颗粒流.这种方法采用一种反馈机制描述刚性边界对流动的影响,算法稳定性依赖于恢复力中引入的自由参数,严重影响了模型计算效率和数值精度.随后,直接力格式的IB 模型被引入LB 模型[12].虽然该模型消除了自由参数对时间步长的约束,但由于重新引入NS 方程中复杂的对流项,LB 模型的优势被破坏.2006 年,Niu 等[13]提出动量交换格式的IB-LB 模型,基于分布函数的动量交换准则计算边界力,完整保留了LB 模型的计算优势.然而,这些传统IB-LB 模型中,显式计算的体积力仅在收敛状态下保证速度场满足无滑移条件[14],导致模拟结果呈现流线穿透物面的伪物理现象.

为了避免流线穿透物面,近15 年来已经发展了各种改进的IB-LB 模型.Wu 和Shu[15]提出一种隐式扩散界面格式的速度修正IB-LB 模型,通过向边界周围流体节点施加速度修正强制无滑移条件.但即使对于二维流动,直接求解矩阵方程仍需较大的内存占用,且矩阵方程可解性强烈依赖于拉格朗日节点分布.Luo 等[16]提出多段直接力IB 模型,通过施加多重直接力强制无滑移约束,可避免复杂的矩阵求逆,且稳定性不受拉格朗日节点分布限制.Kang和Hassan[17]将文献[16]的多段直接力IB 模型与分裂力格式的LB 方程结合,发展了隐式扩散界面的直接力IB-LB 模型.但是针对动边界绕流问题,每个时间步中经固定次数累积施加的边界力严重阻碍了大尺度流动问题的计算效率.Dash 等[18]借助附加参数灵活控制每个时间步中边界力的迭代次数,在保证无滑移条件的基础上大幅减少计算时间.Yang 等[19]在隐式扩散界面背景下改进了动量交换IB-LB 模型.随后几种以分布函数为操作对象的IB-LB 模型[20-22]被发展,相比于以宏观变量为操作对象,这些修正方案增加了原有IB 模型的计算负担.

尽管上述IB-LB 模型的数值预测能力在刚性体绕流问题中已经取得了较大进步,但在可变形动边界绕流问题中仍有待改进,例如非定常流体力的伪物理震荡.如图1 所示,拉格朗日变量描述的边界力扩散向周围流体节点施加体积力,欧拉变量描述的体积力重构流体速度场使边界节点处流体速度和边界速度之间满足无滑移条件.根据Peskin[1]关于IB 数学框架的工作总结,上述信息交互应满足欧拉/拉格朗日变量同一性,即“扩散”应保证欧拉变量描述的体积力和拉格朗日变量描述的边界力等价,“插值”应保证欧拉流体速度和拉格朗日边界速度等价.现有IB-LB 模型中,强制无滑移保证了速度同一性.然而,体积力和边界力之间的同一性没有被强制,这使得预测的流体力呈现伪物理震荡.此外,根据Huang 和Wu[23]关于LB 模型的三阶Chapman-Enskog分析,恢复的宏观方程中出现与体积力二阶梯度相关的附加项,其自由参数与边界力模型直接相关,即边界力和体积力之间的关联将直接影响流动计算的数值精度.

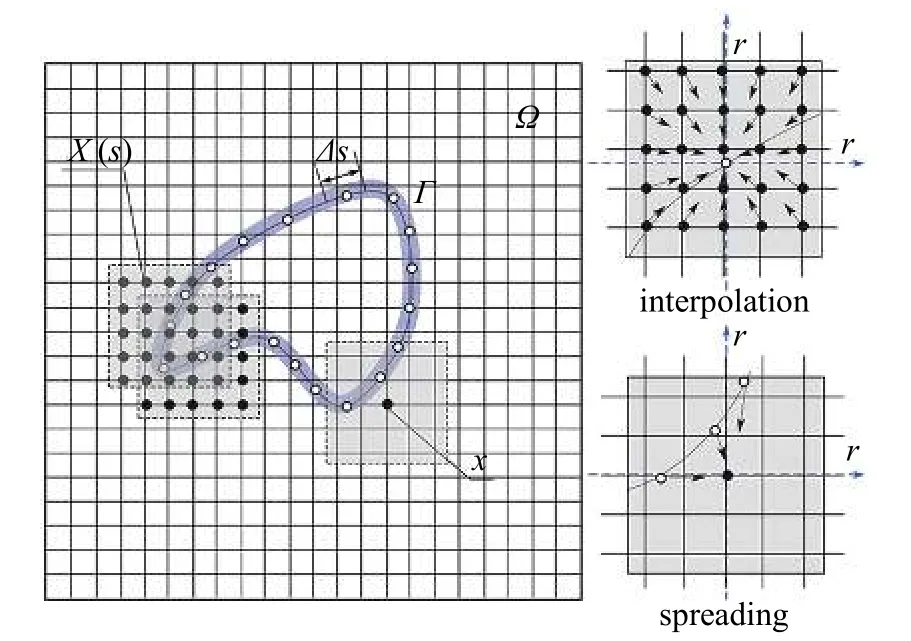
图1 浸没边界方法原理图.○ 代表拉格朗日边界节点;●代表欧拉流体节点Fig.1 Schematic diagram of the immersed boundary method.○ indicate the Lagrangian boundary point;● indicate the Eulerian fluid node

采用隐式扩散界面,本文提出一种改进的直接力格式IB-LB 模型,其中LB 背景下满足力同一性的边界力表达式基于经典IB-NS 模型[1]中的欧拉/拉格朗日变量同一性原则推导.关联边界力与无滑移约束的线性方程组采用Richardson 迭代方法数值求解,有效降低矩阵求逆过程引起的内存占用和计算负担.由附加参数灵活控制子迭代,保证每次时间推进动边界上所有节点的无滑移约束.根据矢量场映射建立描述插值和扩散操作的转换矩阵,简化信息交互界面上的数据交互计算,有效降低IB 模型的代码编写难度.基于改进的IB-LB 模型开发流动求解器,数值计算能力方面完成两个关键改进:一是数值解具备完整的二阶精度;二是抑制了耦合界面上流体力的非物理震荡.本文改进的IB-LB 模型以期为大变形结构体与黏性流体之间的流固耦合动力学算法开发提供理论参考.

1 物理模型

如图1 所示为扩散界面背景下IB 方法的原理图,流体域Ω采用笛卡尔网格离散,浸入流体的物体边界Γ由独立于背景网格的拉格朗日点替代.欧拉流体变量和拉格朗日边界变量通过狄拉克函数关联,相互作用方程如下

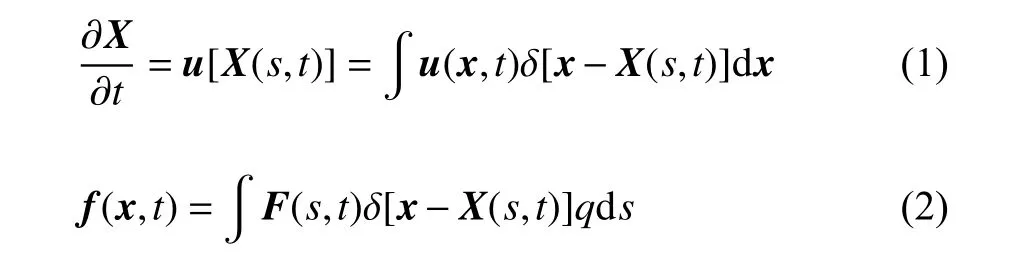
式中,u,f,F分别为流体速度矢量、体力密度矢量和边界力密度矢量,δ代表狄拉克函数,x和X为位置矢量(x∈Ω,X∈Γ),s为拉格朗日坐标,q为边界有效宽度(dxdy=qds[24]).如图1 所示,从欧拉流体节点向拉格朗日边界节点插值速度的过程可理解为:以拉格朗日节点为中心,影响域内所有欧拉节点速度的加权平均.同理,从拉格朗日边界节点向欧拉流体节点扩散体积力的过程可以理解为:以欧拉节点为中心,影响域内所有拉格朗日节点上边界力的加权平均.方程式(1)和式(2)描述了浸没边界和流体之间的相互作用本质.

2 计算模型

2.1 格子Boltzmann (LB)模型

LB 模型使用介观密度分布函数的时空演化描述流体运动,宏观守恒方程中的基础流动变量(密度ρ,速度u,压力p)由分布函数的矩条件简单计算.采用D2Q9 模型[25]离散速度空间 {cα} 定义的速度矢量如下

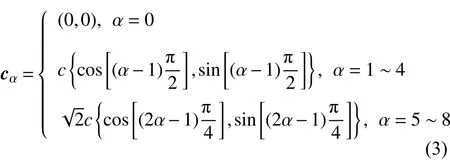
式中,c=Δx/Δt为格子速度,Δx和Δt分别为格子空间尺度和时间尺度.对离散速度空间中考虑体力项映射的Boltzmann 方程沿特征线积分,采用二阶梯形法逼近,获得分布函数演化方程[26]如下

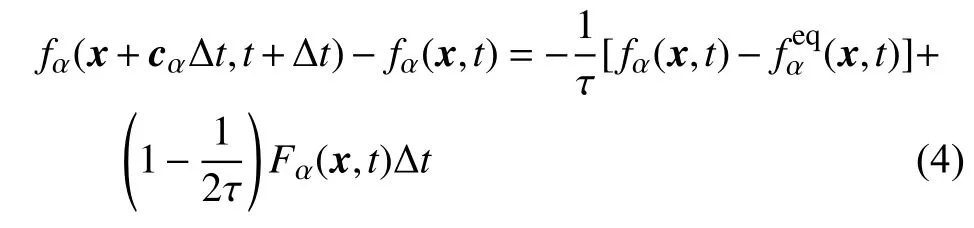
取Maxwell 分布函数在离散速度空间 {cα} 中的二阶速度截断得局部平衡分布函数的表达式

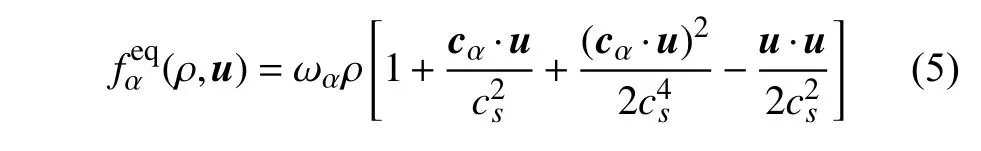
式中,ωα是 {cα} 的加权系数,ω0=4/9,ω1～4=1/9,ω5～8=1/36,cs是模型的格子声速,.

Fα表达式为

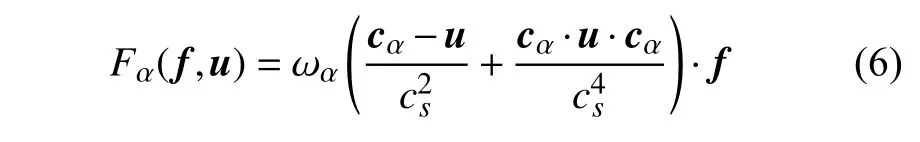
基于上述离散速度模型式(3),分布函数演化方程(4),平衡分布函数式(5)及体力分布函数式(6),采用Chapman-Enskog 展开技术可恢复IB 形式的NS 方程组,且能保证空间和时间上具备二阶精度[27].其中,流体黏度v与弛豫时间τ满足如下关联

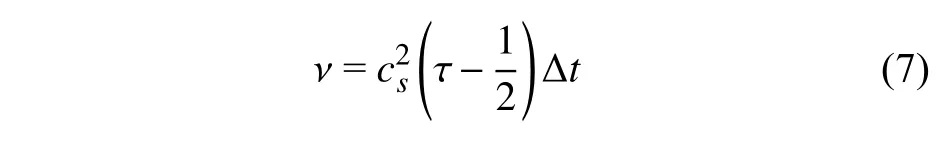
分布函数演化方程(4)右侧碰撞算子描述了流体微团碰撞对分布函数的影响,Fα则描述了宏观体积力在离散速度空间中的投影对分布函数的贡献,即IB-LB 数值格式的时间推进可分解为3 个阶段进行.

(1) 碰撞

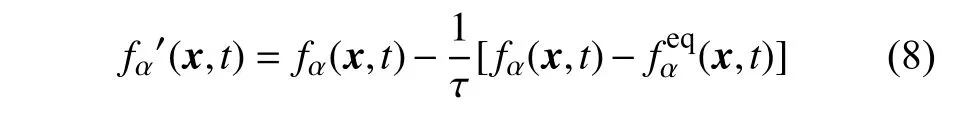
(2) 边界条件施加

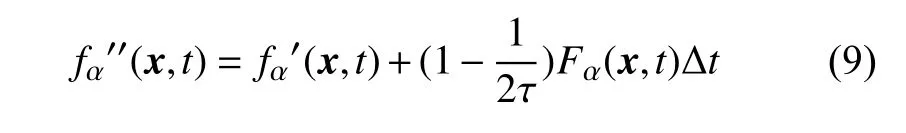
(3)迁移

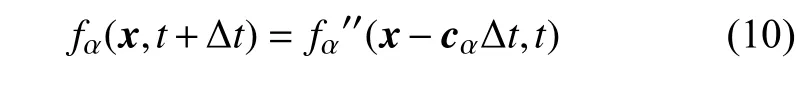
流体的密度ρ,速度u,压力p由迁移后更新的fα的矩方程和等温LB 状态方程计算

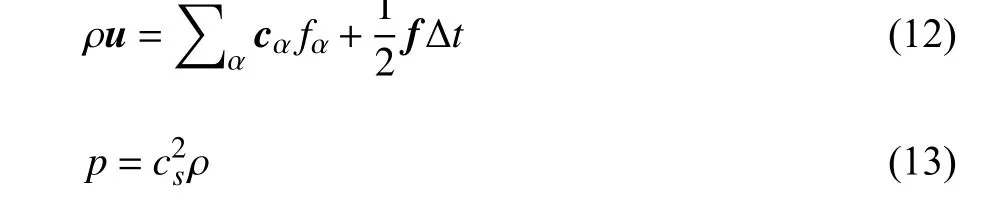
本文采用体力密度的半隐式迭代方案构造流动收敛解.首先给定流场初始条件(ρ0,u0)及体力密度,通过局部平衡分布函数式(5)及体力分布函数式(6)构造初始分布函数,并将与相关的分布函数、密度和速度表示为,和.由于给定的为预估,不能准确满足无滑移条件,因此体积力f和速度u需按照满足无滑移速度约束的边界力进行修正,这个过程由IB 模型来完成.修正后的体力密度和速度为

使用式(14)左侧的f作为新的重复上述操作至收敛.

2.2 信息交互界面

欧拉变量和拉格朗日变量之间的信息交互由离散函数Dlk控制,它被假设为单值变量函数φ的张量积[1],表达式如下

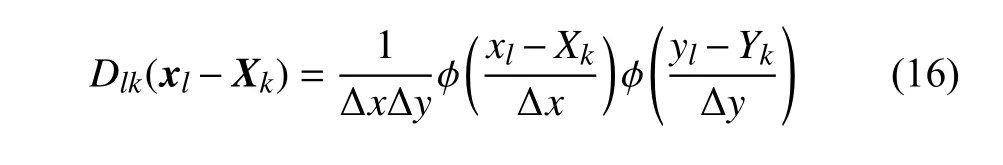
式中,1≤l≤NE,1≤k≤NL.NL为边界上拉格朗日节点总数,NE为所有拉格朗日节点影响域覆盖的不重合欧拉节点总数,影响域尺寸由φ确定.

为保证信息交互界面上相互作用方程式(1)和式(2)的离散具备二阶精度,本文采用式(17)所示的自身满足二阶连续、0～2 阶矩条件及奇偶条件,一阶导数 φ′满足0～2 阶矩条件的分段光顺单值函数 φ[28]构造Dlk.文献结果表明[28],基于式(17)构造的Dlk,直接力格式的IB-NS 模型的数值解具备二阶精度.

可变形运动边界上每个拉格朗日节点具有独立的运动模式,导致大曲率边界附近影响域重叠瞬时变化.为保证每个时间步中任意边界节点处的无滑移条件能够被准确施加,本文发展了一种考虑影响域重叠的界面构造方案,其中心思想是应用离散函数Dlk构造描述信息交互的转换矩阵,耦合相同类型节点间的相互作用.以矢量场映射的方式执行插值和扩散操作,可保证边界上所有拉格朗日节点同时满足无滑移约束,有效抑制影响域重叠引起的震荡源,从而在物面附近生成逐点光滑的速度场

转换矩阵DE和DL的表达式如下

对于刚性静止壁面,DE与DL只需计算一次;对于运动变形界面,每个时间步,由结构运动更新边界位置 {X1,X2,···,Xk,···,XNL} 后,需要重新构造影响域覆盖的欧拉节点集合 {x1,x2,···,xl,···,xNE},并更新NE,然后重新建立DE与DL.

基于上述DE和DL改写相互作用方程(1)和式(2)如下

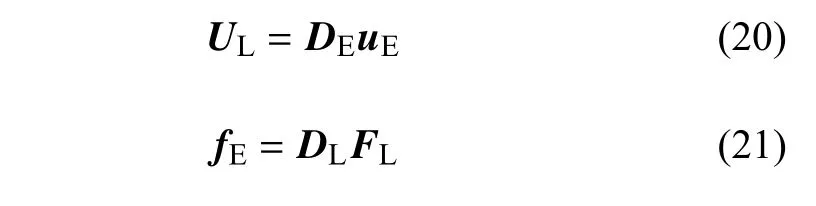
式中,uE={u1,u2,···,uNE}和fE={f1,f2,···,fNE} 是存储在GE中的速度场矢量和体积力场矢量,类似地,UL={U1,U2,···,UNL}和FL={F1,F2,···,FNL}是存储在GL中的边界速度场矢量和边界力密度场矢量.这里,GL表示拉格朗日点构成的边界点集,GE表示所有拉格朗日节点影响域覆盖的不重合欧拉流体点集.式(20)和式(21)以场传递的方式描述了流体-边界之间的相互作用.从编程的角度,基于上述表达,可以在代码中轻松实现并行计算并降低内存占用.此外,通过转换矩阵DE和DL,当前的扩散界面极易拓展至三维流动.

2.3 边界力模型

计算拉格朗日节点处的边界力F并将其扩散至影响域内的欧拉节点是直接力格式IB 模型的核心.受Peskin[1]工作的启发,IB 模型的信息交互过程需满足变量同一性.因此,本文基于LB 框架推导了满足变量同一性的边界力公式,推导过程如下.

首先,根据LB 模型的动量方程(12)构造体积力密度f的直接力表达式

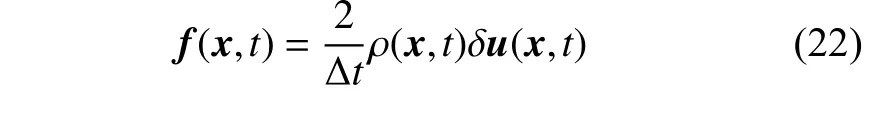
式中,δu=u-u*,δu为欧拉节点处f引发的流体速度修正量,为LB 模型的预计算速度,u为重构的流体速度.

根据力同一性的概念,欧拉/拉格朗日变量描述的浸没物体经历的合流体力等价,即

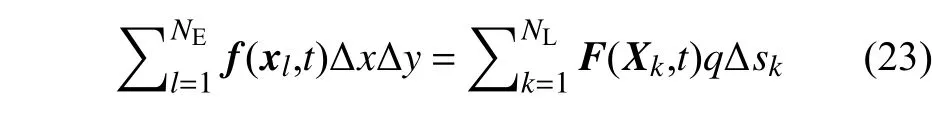
将体积力密度f的直接力表达式(22)带入欧拉变量描述的合流体力,可以发现

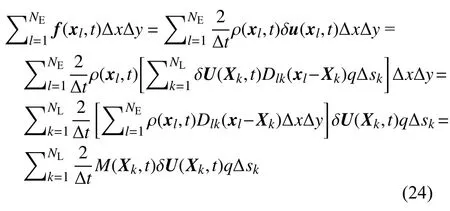
综上得边界力密度F的表达式

GL中拉格朗日节点处流体的质量密度矢量ML={M1,M2,···,MNL}来自欧拉流体节点的质量密度插值

为了保证体积力重构的速度场满足无滑移约束,建立如下方程组

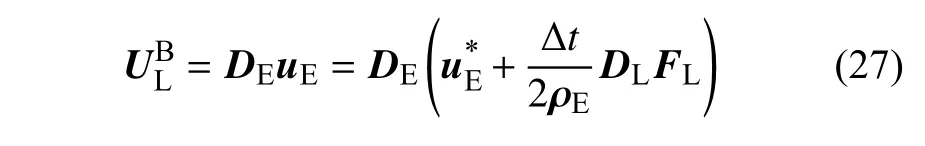
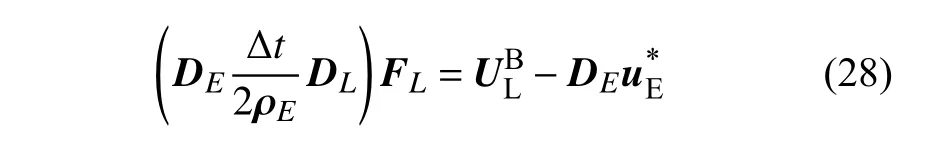
这里,系数矩阵A=DE(Δt/2ρE)DL不仅与GL和GE的位置数据有关,还与GE中存储的密度信息有关;FL是线性方程组中待求解的未知量.

采用Richardson 迭代方法[19]数值求解上述线性方程组

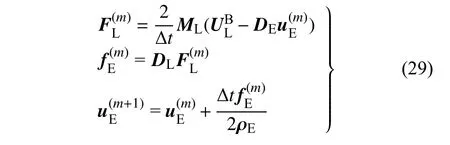
边界力密度FL由子迭代的累和计算

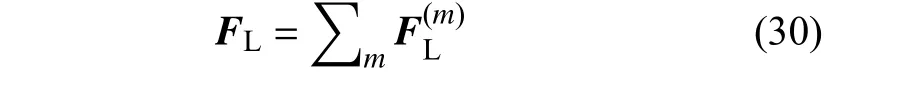
基于上述改进的IB-LB 模型发展流动求解器,算法流程展示于图2.IB 模型以运动界面的位置、速度信息和LB 模型预计算的流体密度和速度场信息为输入变量,任意拉格朗日节点处的局部流体力H作为边界力F的作用反力由IB 模型直接输出,H(Xk,t)=-F(Xk,t)qΔsk,而无需复杂的流体应力积分计算,耦合算法稳定性更高.针对变形体绕流问题,非定常局部流体力H在其气动性能分析中十分关键,本文方法在此类问题的流动模拟中具有很大的应用前景.

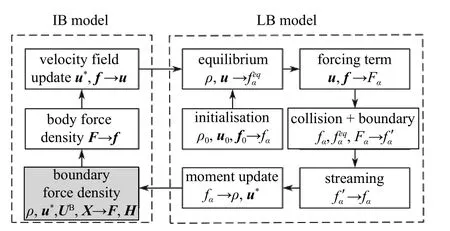
图2 直接力格式IB-LB 模型算法流程图.浅灰色框指明物面参数输出子步骤Fig.2 An overview of one cycle of the IB-LB algorithm with the direct force scheme.The light grey box shows the output sub-step of the surface variables

3 数值方法验证与分析

本节以二维Taylor-Green 涡流、静止圆柱绕流、振荡圆柱绕流及波动翼型绕流4 个经典案例的模拟结果佐证改进的IB-LB 模型的数值精度、预测结果可靠性、及其在复杂运动界面绕流问题中的实用性.

3.1 Taylor-Green 涡流

作为评估算法数值精度的基准算例,Taylor-Green 涡流已由几种不同的IB-LB 模型[15,17,19]执行模拟.理想的IB 模型应具备保持背景LB 求解器固有数值精度的能力.本节采用Taylor-Green 涡流模拟结果来验证本文改进的IB 模型对背景LB 求解器精度的影响.Taylor-Green 涡流在[-L,L]×[-L,L]的计算域中解析解表达式如下

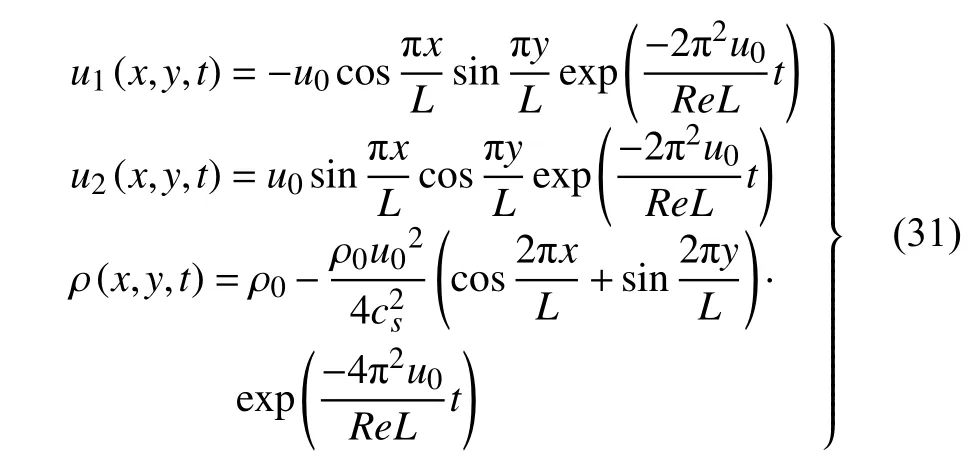
式中,雷诺数Re根据计算域尺寸L和名义速度u0计算,Re=Lu0/ν .为便于比较,本文使用与文献[15,17,19]中相同的参数设置模拟,其中τ=0.65,Re=10,4 种网格尺度(L/h=10,20,40,80)被使用.取t=0 时刻速度和密度的解析解为初始条件,外边界施加周期性条件以确保系统的质量和动量守恒.以计算域中是否添加拉格朗日节点分别执行LB 模型模拟和IB-LB 模型模拟,计算至t=L/u0时刻流场状态.拉格朗日节点处的瞬时由解析解式(31)构造.

式(32) 定义了速度的全局数值误差L2,这里,N是计算域中欧拉流体节点的总数,unum和uexa分别为速度的数值解和精确解.数值精度通过数值误差L2与网格尺度h的对数斜率来量化

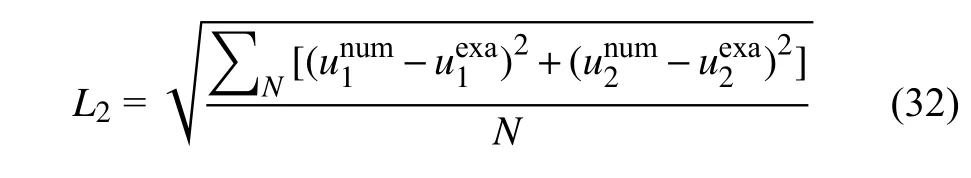
为了说明本文模拟结果在精度方面的改进不针对扩散界面中使用的某一特定单值函数,分别采用4-point cosine[15],4-point piecewise[17]及5-point smoothed piecewise (式(17))单值函数构造满足力同一性的IB-LB 模型执行本算例.图3 展示了对数坐标下的数值误差L2与网格间距h,3 组IB-LB 模型数据与LB 模型数据几乎完全重合.其中,无拉格朗日节点嵌入的LB 模型的斜率为2.017,嵌入拉格朗日节点的IB-LB 模型的斜率分别为2.010,2.013 和2.014.基于相同的LB 背景,速度修正IB-LB 模型[15]采用4-point cosine 单值函数构造Dlk,数值精度为1.9,多段直接力IB-LB 模型[17]和动量交换IB-LB 模型[19]采用4-point piecewise 单值函数构造Dlk,数值精度分别为1.98 和1.99.当前结果表明,力同一性可改善IB 模型对LB 结果精度的弱化,改进的IB 模型完整保留了背景LB 模型求解器的数值精度.同时,当前IB-LB 模型流动求解器代码可以为本文计算模型提供可靠的数值解,计算模型具有二阶数值精度.

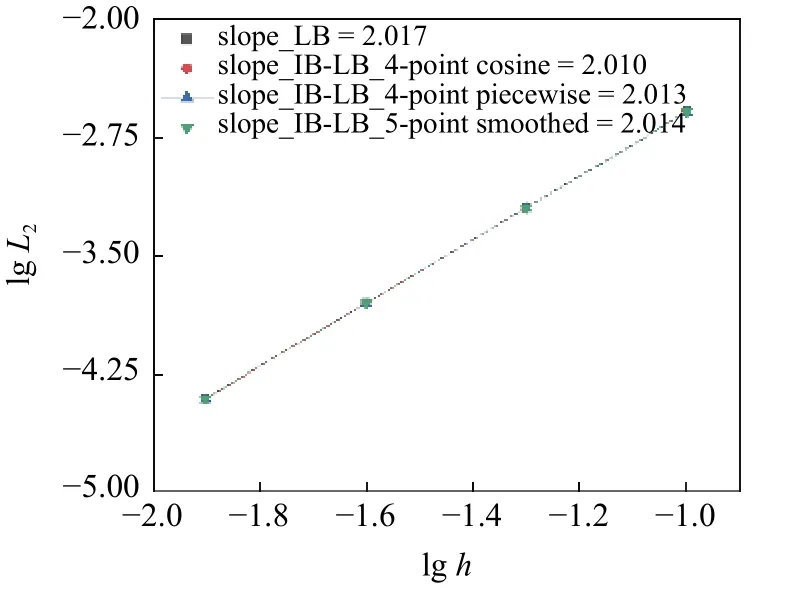
图3 对数坐标下的速度误差L2 与网格尺度hFig.3 Numerical error L2of velocity versus mesh spacing hfor Taylor-Green flow using the present IB-LB model with different φand the standard LB model

3.2 静止圆柱绕流

因其流动结构由雷诺数唯一确定,圆柱绕流作为基准算例在复杂边界处理问题中被广泛应用.设定流动参数U∞=0.1 和D=1.0,通过改变运动粘度v调整雷诺数Re=DU∞/ν,一系列模拟被执行.计算域尺寸为30D× 15D,圆柱位于计算域对称线,圆柱中心到入口边界的距离为13.5D.入口边界施加Dirichlet 条件,出口边界施加Neumann 条件,自由剪切条件应用于侧边界.流场初始条件指定为ρ0=1.0 和u0=(U∞,0).采用网格间距h=1/N均匀划分背景网格,N为圆柱直径占据的格子数,本节算例N=75,网格收敛指数(GCI)结果显示当前网格间距满足收敛性要求.

首先,通过与文献结果进行比较验证了本文改进的IB-LB 模型模拟结果的准确性.表1 列出Re=20 和Re=40 条件下无量纲规则区长度2Lw/D和阻力系数的数值解,其中FD为圆柱阻力,.对比结果表明,本文结果与现有研究中的数值模拟结果[15,17,19-20]具有良好的一致性.我们进一步调整计算域至40D× 40D(具有相同的网格间距)重复当前模拟,阐明外边界对计算结果的影响.结果表明,横向距离的增加会导致阻力系数降低,循环区长度增加,但相对误差很小,即30D× 15D的计算域尺寸下模拟结果可靠.

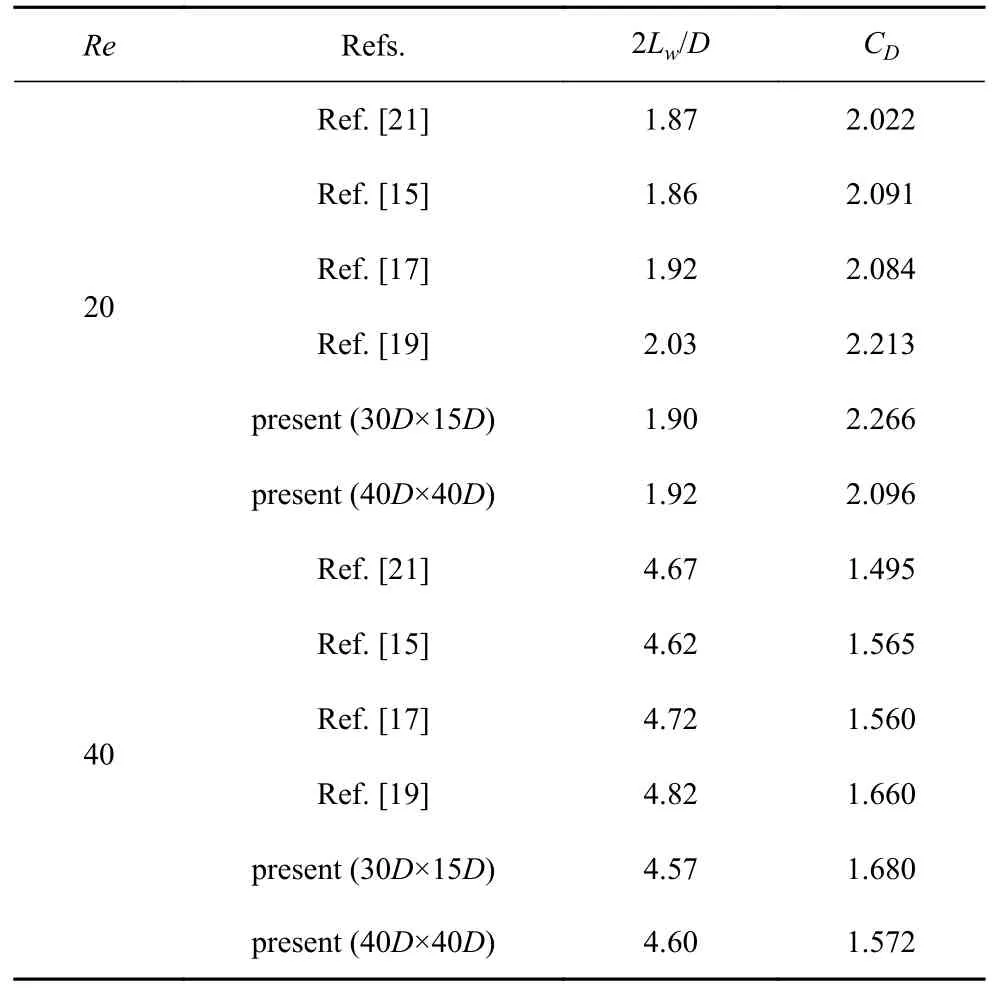
表1 Re=20 和40 时规则区长度和阻力系数与已有文献结果的比较Table 1 Comparison of the obtained recirculating length,the drag coefficient with the previous results at Re=20 and 40

图4 展示了Re=20 和40 条件下,二维圆柱表面压强系数CP与方向角θ的关系曲线,方向角自前驻点θ=0°经圆柱上方指向后基点θ=180°,Cp(θ)=.图4 中压强分布曲线光滑无震荡,且当前模型结果与前人研究结果[14-15,29]吻合良好,压强极大值出现在前滞点(θ=0°),压强极小值位于分离点附近,圆柱背后分离区压强有所回升,以上结果验证了本文改进的IB-LB 模型能够为复杂结构外形上的拉格朗日节点提供光滑、可靠的压强预测.

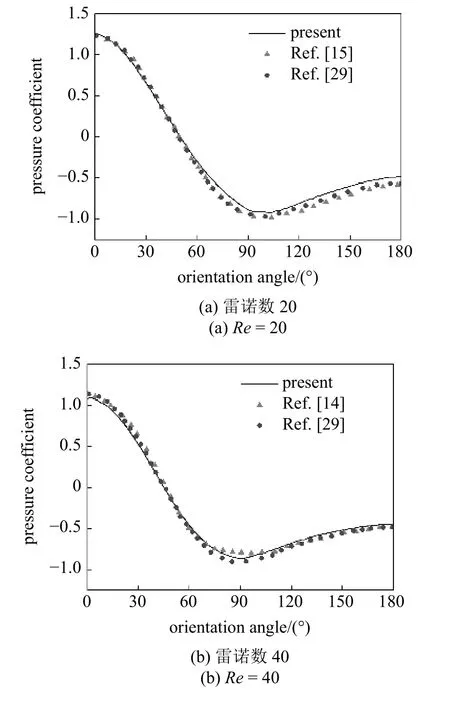
图4 圆柱表面压强系数与方向角关系曲线Fig.4 Pressure coefficient curve of cylinder versus the orientation angle

图5 为Re=20 和100 时,圆柱附近的流线分布.当Re＜ 47,圆柱背后出现稳定的对称漩涡;当Re＞ 47,定常流逐渐发展为非定常流.数值结果表明,子迭代中引入的自由参数ε不会影响模型的数值精度,但其取值直接影响了壁面流线是否泄露.本文所有模拟取 ε=10-8求解的边界力数值解能够保证每个时间步中无滑移边界条件准确施加,精确满足无滑移约束的速度场抑制了流线穿过圆柱体表面,如图5 中所示.图5(a)展示的定常流中,二维圆柱内部包含两对对称的环形流线,圆柱背后分布着稳定的对称规则区,规则区长度列于表1.图5(b)展示的非定常流中,可观察到柱面背后波动的漩涡,圆柱体内部的环形流线随表面脱落的涡旋同步波动.当前数值结果验证了本文改进的IB-LB 模型可在灵活控制迭代次数的基础上保证无滑移条件准确施加.

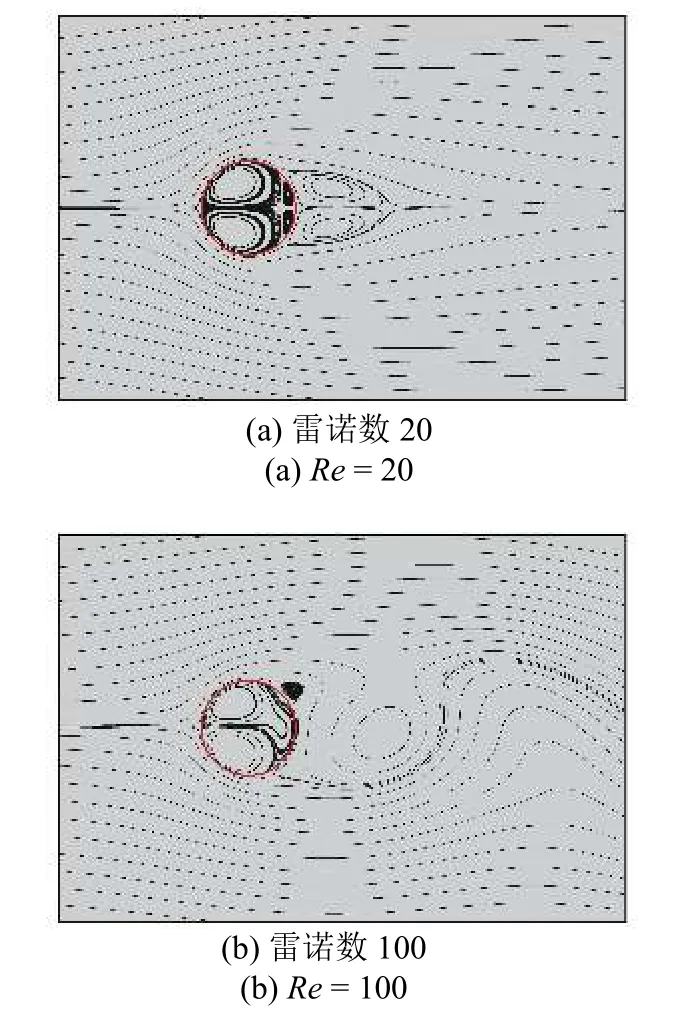
图5 圆柱周围流线分布Fig.5 Streamline distribution near the cylinder.

表2 列出了Re=100 时,本文模拟获得的圆柱表面时均阻力系数、升力系数幅值,及斯特劳哈尔数S t=Dfvs/U∞数据与现有文献结果[15,17,30-31]的比较.fvs为圆柱表面涡脱频率,通过侧向力系数CL的快速傅里叶变换获得.对比结果表明,本文模型获得的数值解与文献中实验、数值计算模型的结果吻合良好,验证了本文改进的IB-LB 模型针对复杂边界外形绕流的非定常流动演化问题预测结果的有效性.

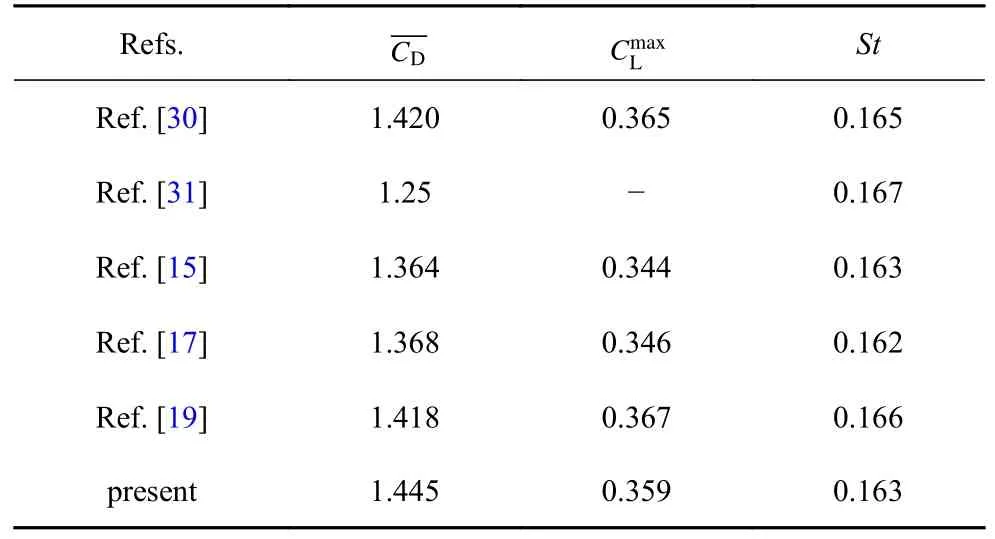
表2 Re=100 的当前模型与其他方法的流动特征参数比较Table 2 Comparison between the present model and other methods at Re=100

3.3 流动经过强制振动圆柱

在上述Re=40 的定常流动中,强制二维圆柱执行周期性的侧向振动扰动周围流体,圆柱体的侧向振荡由如下正弦函数控制

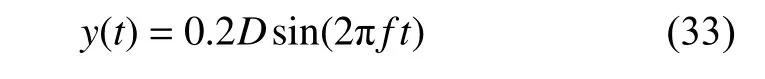
式中,f为振荡频率,圆柱振荡特征数St=Df/U∞=0.15.在圆柱的受迫振动扰动下,Re=40 的定常流动逐渐发展为周期性的非定常流动,涡旋脱落频率为fvs=0.915f.

图6 显示了振荡圆柱经历的非定常阻力系数随圆柱中心位置变化的相图.采用传统多段直接力格式的IB-LB 模型[17]执行当前模拟,获得的结果被展示于图6(a),本文改进模型的模拟结果绘制于图6(b).如图6(a)所示,传统直接力格式的IB-LB 模型的预测结果中,随圆柱振动作用于圆柱表面的流体力合力中呈现伪物理震荡.相反,本文改进模型获得的非定常流体力随圆柱振动平滑波动,说明满足力同一性条件的IB-LB 模型能够有效抑制模拟结果中非定常流体力的伪物理震荡.此外,本文改进的IB-LB 模型具备预测动边界诱导非定常流动演化的能力.

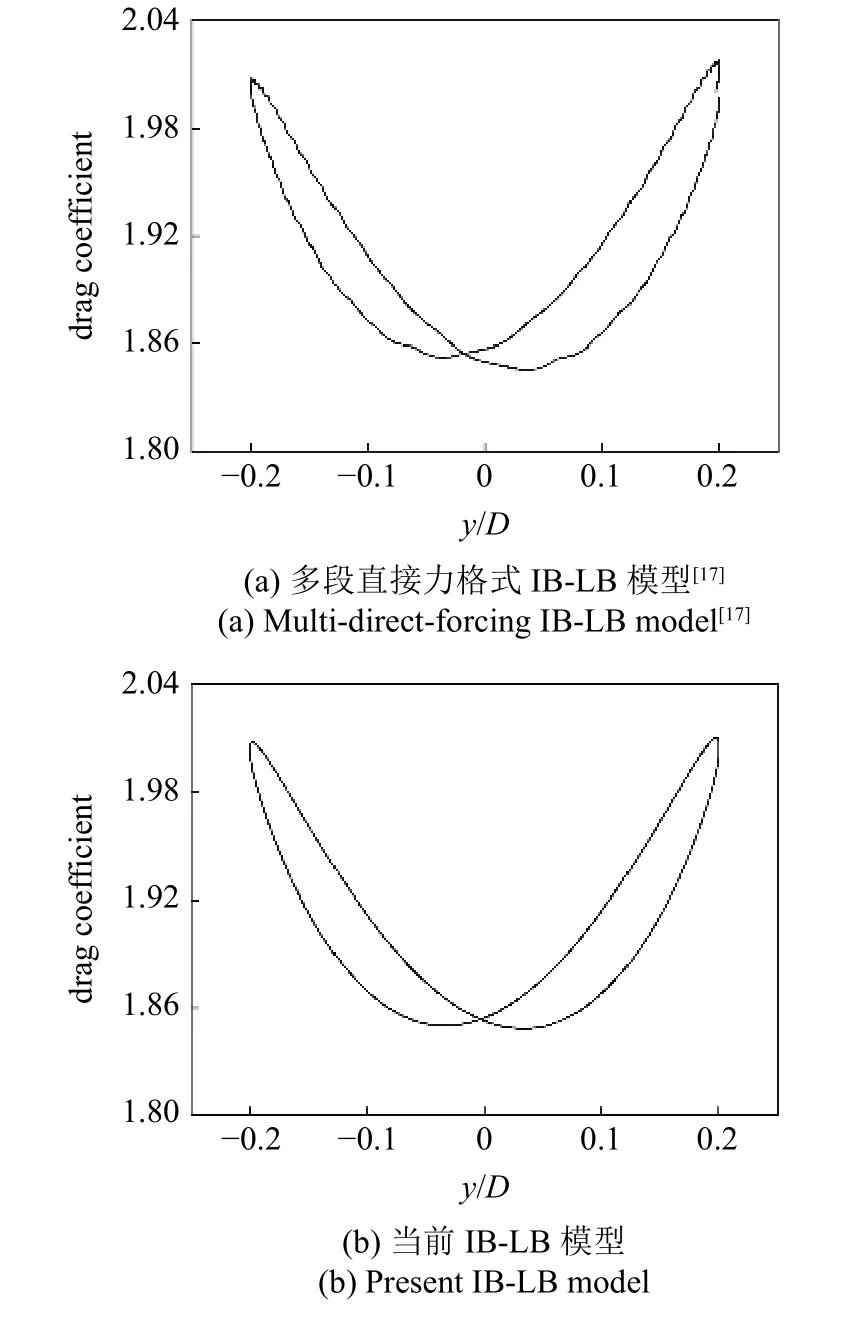
图6 振荡圆柱阻力系数与圆柱中心位移的关系Fig.6 Drag coefficient acting on the oscillation cylinder versus the position of the cylinder center

我们比较了速度修正格式IB-LB 模型[15]和本文改进的IB-LB 模型在每个时间步推进中花费的平均CPU 占用时长tib-lb,以说明模型的计算效率.这里,tib-lb是流动求解器一个完整的时间步推进所占用的CPU 时长,其中包含了IB 模型和LB 模型的CPU 占用.由于背景LB 是相同的,tib-lb的比较结果同样可以定量评估两种IB 模型的效率.两组模拟在相同的工作站上执行,计算环境参数如下,CPU:Intel Xeon(R) Silver 4214 CPU @ 2.2 GHz 2.19 GHz;内存:DDR4 2400ZHz 16 GB × 4.针对Re=40,St=0.15 的振动圆柱绕流算例,速度修正IB-LB 模型的tib-lb为0.126 s,本文改进模型的tib-lb为0.089 s.当前结果验证了本文改进IB-LB 模型的计算效率优势.

3.4 波动翼型绕流

本节模拟可作为上述振荡圆柱诱导周围流体演化的非定常流验证算例的拓展,区别在于波动翼代表了刚-柔运动叠加的可变形复杂运动边界,此外在翼型前缘和尾缘附近带有较大的曲率半径,可验证本文模型对此类问题的处理能力.均匀流中波动的NACA0012 翼型表面的非定常流体力和流场涡量云图阐明了当前模型在大变形结构流固耦合动力学问题中的预测结果可靠性,算法的实用性及可拓展性.

由平移、旋转和波动行波方程的叠加强制翼型振荡,各行波分量由相同的运动频率f控制,且各子运动间的相位差恒定,翼型波动的特征数S t=L f/U∞=0.54,L为翼型弦长,L/h=100.

侧向平移行波方程如下

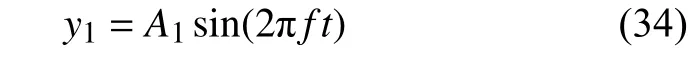
式中,侧向平移幅值A1=0.15L.

旋转运动以距离翼型前缘点0.3L的位置为转动中心,旋转运动行波方程为

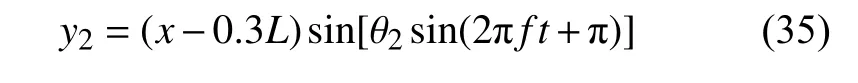
式中,旋转幅值θ2=7.75°.

波动运动自距离翼型前缘点0.4L的位置起执行,侧向波动幅值A3(x/L)为x坐标的二次函数[32],波动行波方程为

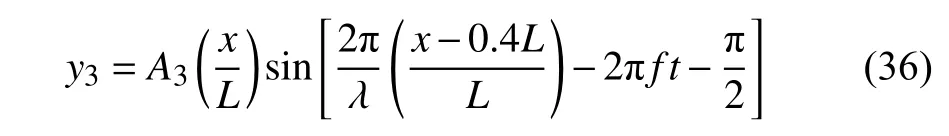
式中A3(x/L)=0.01L(x/L-0.4)+0.51L(x/L-0.4)2.

经过10 个翼型运动周期,流场表现出稳定的周期性,其周期特性通过时变的流体力和功率参数描述.图7 展示了作用于波动翼型表面的瞬时推进力系数随时间变化曲线.在波动特征数St=0.54 条件下,周围流体不能为波动翼提供推进,整个运动周期中翼型始终承受流体施加的阻力作用(CT＜ 0).瞬时变化的复杂外形承受的流体力合力随时间变化趋势类似于侧向平移行波曲线的波动趋势,曲线光滑无震荡,说明当前模型能够准确预测作用在复杂外形动边界上的非定常流体力,其数值解中没有出现伪物理特征.

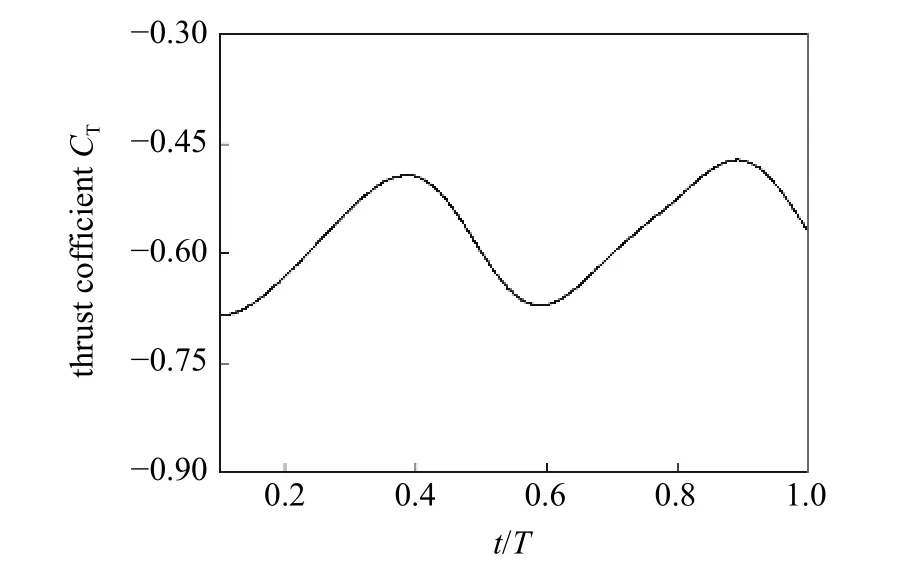
图7 波动翼型的时间相关推力系数Fig.7 Time-dependent thrust coefficient acting on the undulatory foil

图8 展示了维持翼型复合运动的运动功率系数CPS,克服运动阻力的功率系数CPD,以及维持运动的总功率系数CPT随时间变化曲线.其中,运动功率系数CPS根据如下公式计算

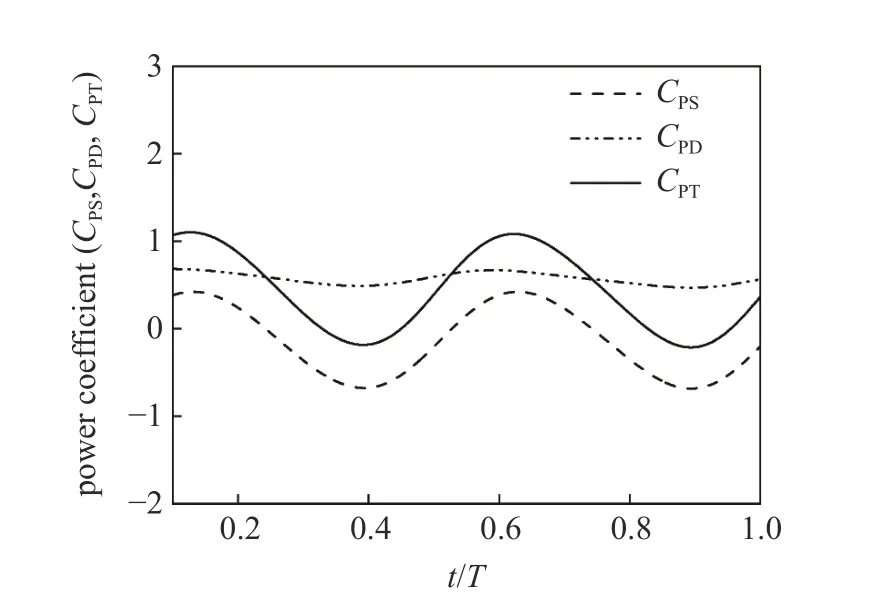
图8 波动翼型的时间相关运动功率系数、阻力功率系数和总功率系数Fig.8 Time-dependent kinematic power coefficient,overcome drag power coefficient,and total power coefficient required by the undulatory foil

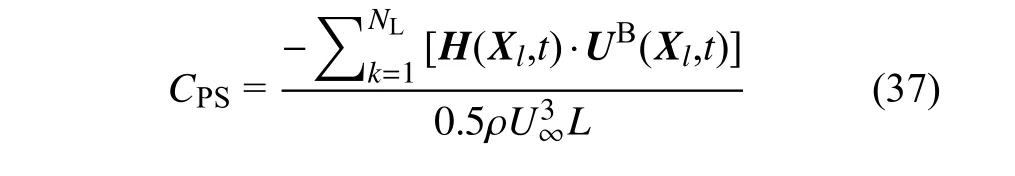
式中,H(Xk,t)为流体施加在第k个拉格朗日节点的局部流体力,UB(Xk,t)为在第k个拉格朗日节点的运动速度,由复合运动行波方程的时间导数计算.克服流体阻力的功率系数,总功率系数CPT为CPS和CPD的和,CPT=CPS+CPD.图8所示的数值结果表明,维持波动翼型运动所需的CPS,CPD,CPT系数具备类似于推进力系数CT的周期属性.与运动功率系数CPS相比,抵抗流体阻力所需的功率系数CPD在总功率系数CPT中的占比很小.CPT的波动趋势与CPS的波动趋势一致,当CPT与CPS同时出现最大值时,CPD为最小值,说明波动翼通过运动功率消耗完成了阻力减.这一结论与鱼游模拟的数值实验结果[32,33]一致.

图9 展示了波动翼型周围的涡量云图,根据一个运动周期内流场的瞬时涡量图可知,波动翼型周围产生了周期性变化的剪切层.剪切层没有在翼型后缘附近发展流动分离,而是在翼型背后大致1.5 倍弦长的位置形成核心涡脱落进入尾迹.交替的符号相反的漩涡在波动翼尾迹中形成经典的卡门涡街.已有研究结果表明,单一的侧向平移运动会在前缘两侧生成交替的逆向旋转的漩涡,这一结论与图9中的涡量云图结果相悖.一个合理的解释是,柔性波动运动抑制了前缘附近刚性扑翼运动(平移+旋转)诱导的漩涡发展,在翼型两侧的剪切层中流体不稳定性被削减,不足以支撑交替漩涡的形成.而在波动翼的背后,符号相反的剪切层间相互作用增加了彼此携带的流体不稳定,从而在波动翼型背后形成卡门涡街.

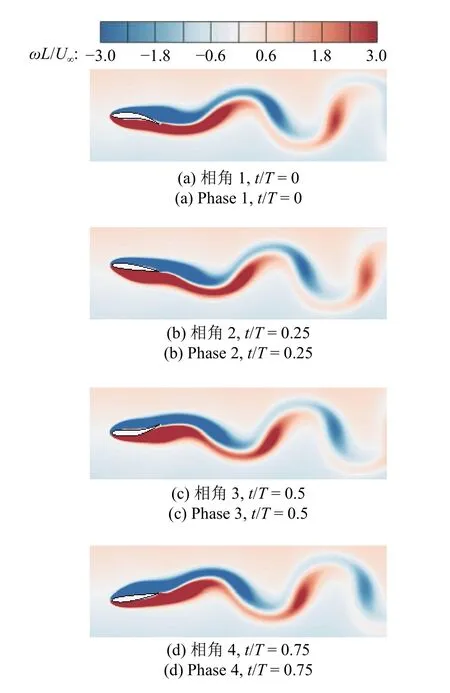
图9 均匀流动中复合运动翼型周围涡量云图Fig.9 Vortex contour near the swimming foil in a uniform flow

4 结论

本文针对可变形动边界绕流的流固耦合动力学问题,在隐式扩散界面背景下,提出一种改进的直接力格式IB-LB 模型.保留IB 方法在宏观流场中通过向边界附近流体施加体积力干扰速度场分布的思想,浸没边界对流场施加的体积力由使无滑移速度约束准确施加的边界力决定.借助狄拉克函数满足的矩条件,从LB 模型的体积力表达式出发,推导满足力同一性的边界力表达式.LB 背景下,力同一性的数学内容是,拉格朗日节点向周围欧拉节点的速度修正量扩散是欧拉节点向拉格朗日节点的质量密度插值的伴随.满足力同一性的IB 模型不仅完整保留了LB 模型的原有二阶精度,而且有效抑制了非定常流体力的伪物理震荡.另一方面,根据离散的狄拉克函数建立描述插值和扩散操作的转换矩阵,重叠的影响域中同类型变量被耦合,保证每个边界节点处的无滑移速度约束条件准确施加.表征无滑移条件的线性方程组采用迭代方法求解,无需矩阵求逆,降低计算负担,算法稳定性不受拉格朗日节点分布约束.