折纸结构和折纸超材料动力学研究进展1)

方虹斌 * 吴海平 * 刘作林 *, 张琦炜 徐 鉴 ,

* (复旦大学智能机器人研究院,上海 200433)

† (同济大学航空航天与力学学院,上海 200092)

引言

折纸(origami)结构起源于中国的折纸艺术,其在日本得到了长足发展.如今,折纸结构不再局限于“纸张”,而是泛指一切将二维薄片通过折叠(folding)形成的三维结构,其受到了教育学家、数学家、建筑学家、物理学家和工程科学家们的广泛关注.折痕图(crease pattern)是所有折纸结构的起点,其具有无穷的设计空间,可以据此折叠出复杂、精妙的三维结构.因此,近些年来,学者们提出了许多折纸启发的结构:从大尺度(≥100m)的可展开航天结构[1-2]和折叠建筑[3-4],到中等尺度(10-3～10-1m)的自折叠机器人[5-6]和自折叠生物医学器件[7-8],到小尺度(≤10-4m)的微纳折叠元件[9-10]等.

受到折纸结构研究的催化,“折纸超材料(origami metamaterial)”应运而生.当前,随着增材制造尤其是3D 打印技术的迅速发展,材料的设计和研发进入了“超材料(metamaterial)”阶段.超材料具有自然界材料和工程结构所不具有的特殊性质,其特殊性质不是来源于化学组分,而是来源于精密设计的几何结构和尺寸大小.力学(机械) 超材料(mechanical metamaterial)是超材料家族中的重要一类,具有自然界材料和工程结构所不具有的特殊力学性质[11-12].对于折纸超材料而言,是由精心设计的折纸结构堆叠、排列而成,折叠对于折纸超材料某些力学特性的形成具有决定性意义.

折纸结构和折纸超材料由于其异常广阔的设计空间和突出的大变形、拓扑变化等性质,在最近几年内迅速成为材料、智能结构、机器人等领域的研究前沿和热点.2012 年和2013 年,美国国家科学基金会(NSF)和美国空军科学研究办公室(AFOSR)连续两年在前沿研究计划(emerging frontiers in research and innovation,EFRI)框架下发布以“面向工程变革的一体化自组装系统折纸结构设计(origami design for integration of self-assembling systems for engineering innovation,ODISSEI)”为主题的研究方向[13].EFRI-ODISSEI 共资助项目13 项,总计资助经费2900 余万美元,平均每项经费为223 万美元,项目周期2～ 9 年,项目研究对象涵盖折纸超材料、主动折纸技术、基于折纸的人体组织工程、可重构折纸结构、基于折纸的新型光学器件等(表1).自2014年以来,折纸结构和折纸超材料研究取得许多重要创新性成果,已在《Science》、《Nature》和《PNAS》上发表论文44 篇,更有大量的论文出现在以《Advanced Materials》为代表的材料学顶尖刊物和以《PRL》为代表的物理学顶尖刊物上(图1).图2 展示了在Web of Science (WOS)数据库中,以“origami(排除DNA)”为主题搜索的期刊、会议和综述论文数目及其引用量在2001 年至2020 年间的演变趋势.近20 年来,在折纸领域发表的论文数目增长了近110 倍,引用量从2001 年的0 次跃升至2020 年的10 654 次,这充分表明学术界对折纸这一前沿研究领域的兴趣迅速上升.特别是,随着EFRI-ODISSEI项目于2012 年和2013 年启动,以“origami”为主题的发文量和引用量迅速增长,呈现出明显的拐点.此外,折纸界的“奥林匹克”会议“International Meeting on Origami in Science,Mathematics and Education(OSME)”每4 年召开一届,吸引了全世界著名学者参会并汇报他们的研究进展,每届会议出版文集《OrigamiN》.注意到,会议文集厚度逐次增长,《Origami3》(2002 年)为单卷366 页,《Origami4》(2006 年)为单卷572 页,《Origami5》(2010 年)为单卷668 页,《Origami6》(2014 年)为两卷共735 页,《Origami7》(2018 年)为4 卷共1357 页,这也从一个侧面反映出折纸相关研究的热度和受关注度.

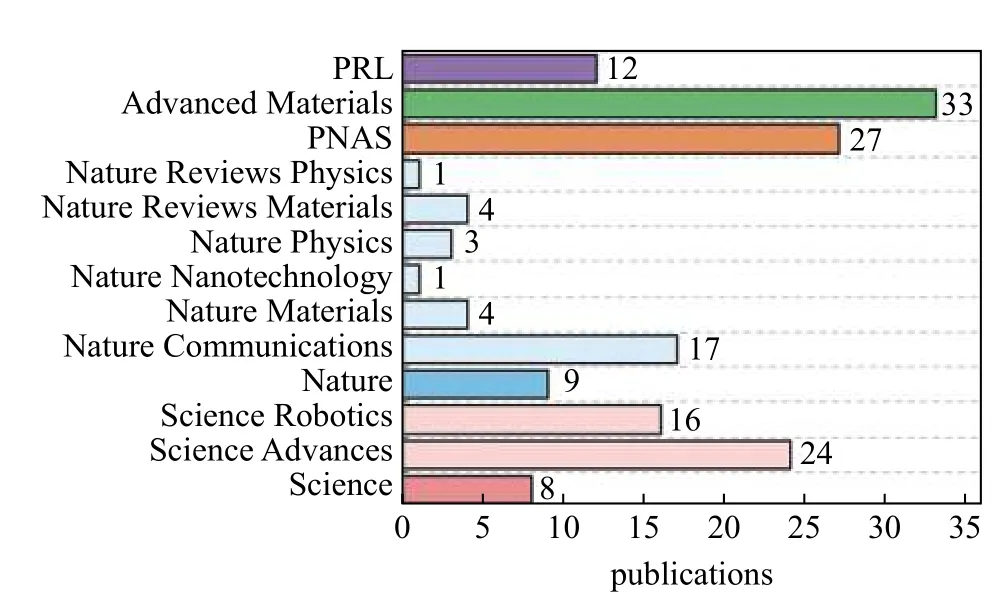
图1 2014—2021 年间在顶级期刊上发表的以Origami 为主题的论文Fig.1 Papers on origami published in top journals during 2014—2021

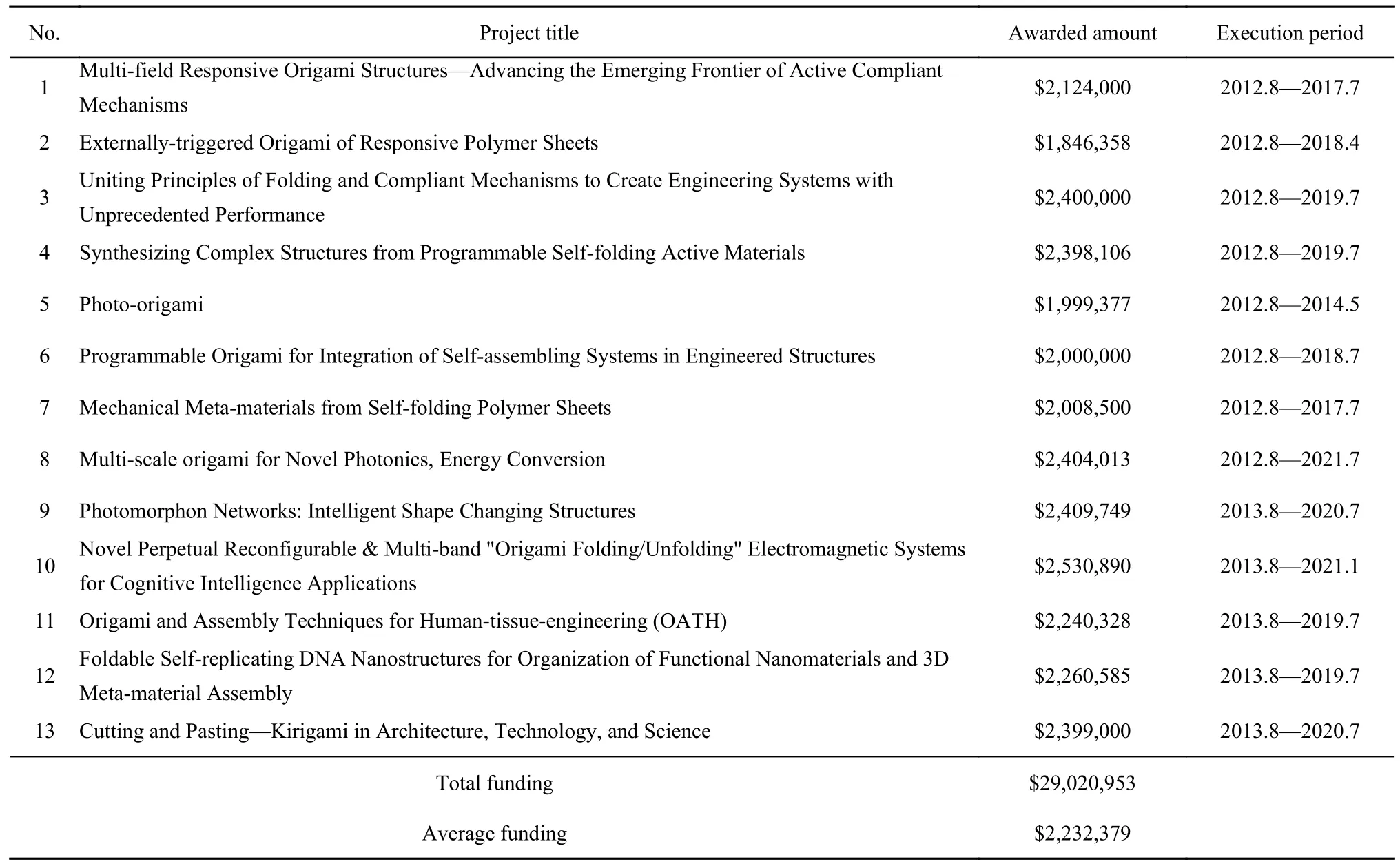
表1 EFRI-ODISSEI 资助的项目[13]Table 1 Projects funded by EFRI-ODISSEI[13]

中国也高度重视折纸结构这一前沿研究领域,自2018 年起在多个国家重大研究计划中立项支持,但支持方向较为狭窄,支持强度也较小.2019 年,国家重点研发计划“智能机器人”重点专项发布指南“基于编织/折展原理的机器人结构功能一体化设计”,其支持项目数为1 项,经费约500 万元;2021年,国家自然科学基金委员会发布“十四五”第一批重大项目指南,其中工程与材料科学部发布指南“瞬态折展变形机构设计理论与关键技术基础”,支持项目数 ≤1 项,直接费用预算不超过1500 万元.相对应的,我国学者在折纸领域的发文数量明显少于美国.在上述统计的以“origami”为主题的论文中,中国学者发表的论文仅占20.5%,获得的引用量占比为22.2%(图2),远低于美国的44.2%和57.8%.

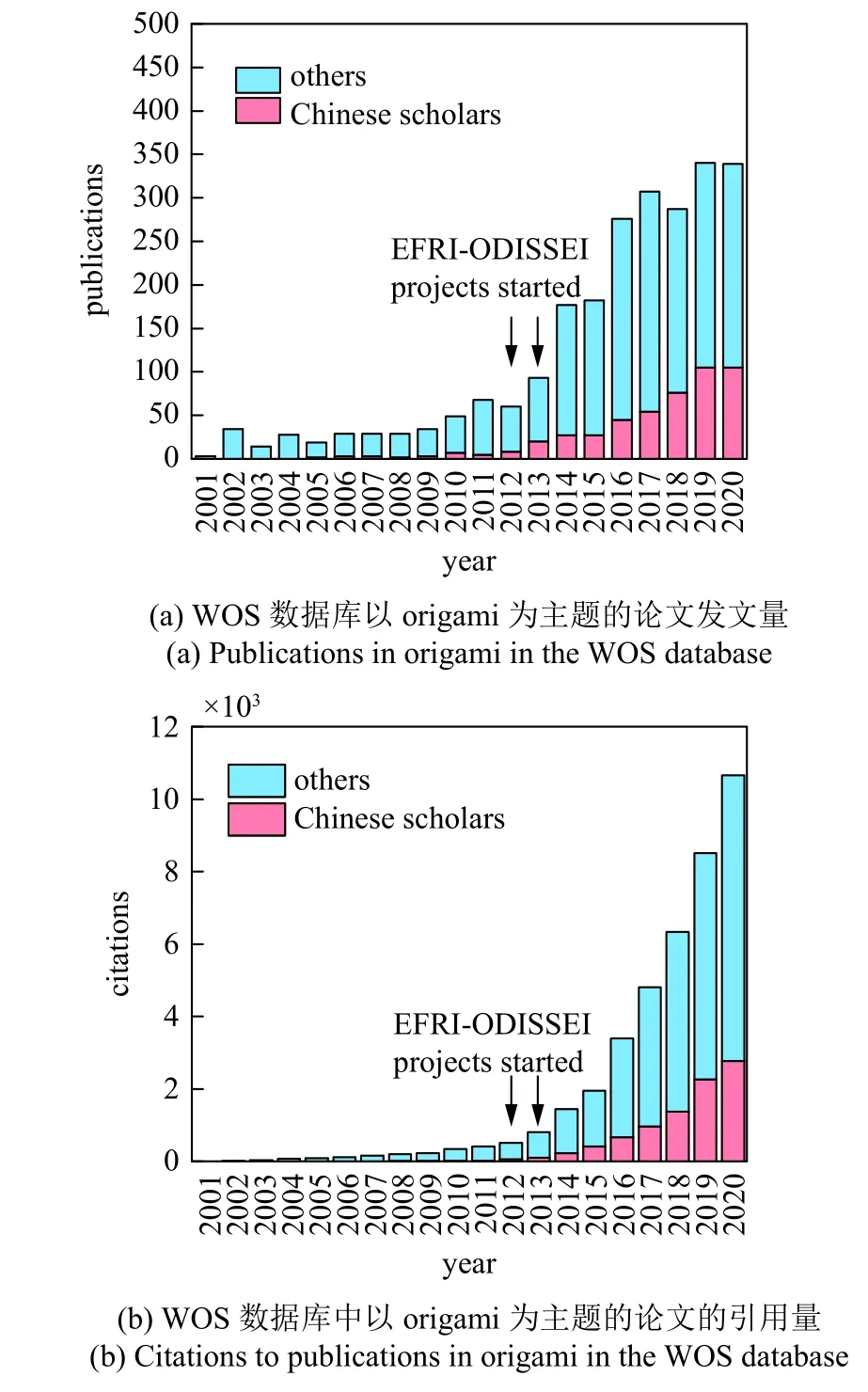
图2 以Origami 为主题的研究发展历程分析Fig.2 Analysis of the development process of origami-themed research

除了基础研究和论文发表,折纸结构和折纸超材料也具有巨大的工程应用潜力.事实上,目前已有许多折纸器件面世并得到应用,包括折纸型能量吸收护栏[14]、折纸型血管支架[8]、折纸型空间展开结构[15]、折纸机械臂[16]、折纸蠕虫机器人[17]、折纸吸振材料[18]和声调控折纸超材料[19]等.这些应用主要利用了折纸结构和折纸超材料的超轻、超大变形、变构型和变拓扑等特征.例如,可展开航天结构在发射过程中处于折叠收拢状态,固定安置在运载工具有效载荷舱内,体积最小,待发射入轨后,由地面指挥中心控制结构按设计要求展开成一个大型复杂航天结构[1];自折叠机器人通常由平面材料制成,通过折叠形成复杂的三维构型而实现功能[6];折纸声学器件可以通过调整拓扑,实现对声波透射和反射等的调控[20-21].注意到,上述这些特征常由折叠运动所诱发,具有尺度无关性和组分无关性.因此,几何设计和运动学分析一直是折纸结构和折纸超材料基础研究和应用研究的重点之一.

为将折纸结构和折纸超材料应用于实际工程,静力学和准静态行为分析也不可或缺,常需要明确折纸结构和折纸超材料在不同方向上的力-位移本构关系,实现大变形和大承载间的协调.静力学研究的另一个主要关注点就是折叠诱发的超常规静力学特性.例如,折叠可以带来丰富的变形模式[22],可以实现负泊松比[23-24]、负体积模量[25]等特征;折纸结构常具有几何非线性和几何“一对多”关系,可以实现非线性本构[26]、双稳态[24,27]和多稳态[28-29]等特性;折叠运动会由于折面的接触而停止,使得结构进入弹性变形模式,诱发刚度跳跃特性[30].通过调控折纸超材料中的单胞的变形,实现力学特性的可编程性[31-32]也是当前研究的热点方向之一.

此外,折纸结构和折纸超材料也将不可避免地在动力学环境中工作,迫切需要研究由折叠诱发的动力学行为.例如,折纸器件将有可能受到基础激励,需要考查位移传递率等稳态动力学特性;航天可折展结构的展开部署本质上是一个瞬态动力学过程,需要关注稳定时间和超调量等瞬态动力学指标;折纸超材料本身还可以作为波传播的媒介,需要探讨带隙等波动力学特性;折纸机器人在工作中有可能受到外界撞击或从高处跌落,需要分析冲击吸收功等冲击力学特性.但是,相比于设计、运动学和静力学研究,折纸结构和折纸超材料的动力学研究起步较晚,面临较多挑战.目前,折纸动力学研究主要针对特例设计和分析,主要关注点有4 个方面:(1)折纸结构中由全局强几何非线性本构(例如,准零刚度[18]、双稳态[27,33]等)引起的复杂动力学行为及其应用;(2)折纸结构在展开或构型切换过程中的瞬态动力学行为[34-36];(3)折纸结构和折纸超材料在冲击载荷下的动力学行为[14,37];(4)折纸超材料作为波传播媒介的波动力学特性[38-39].

总的来说,折纸结构和折纸超材料动力学研究的方法框架还不成熟和完善,在动力学建模和参数辨识、动力学理论和实验分析方法、超常规动力学行为机制解析等方面都面临较大挑战,也充满机遇(详见第6 节).考虑到折纸结构和折纸超材料的设计、运动学和静力学已发展得较为成熟,并已有多篇综述关注[40-45],本文主要关注折纸结构和折纸超材料动力学.但是,为了使本文具有完整性,下面首先简要介绍折纸结构和折纸超材料的几何设计与静力学、运动学特性.随后,本文从动力学建模、动力学分析和实验方法、折叠诱发的超常规动力学特性和动力学应用等方面对国内外相关研究成果和最新进展进行回顾,并梳理值得关注的若干问题,为相关的研究者提供参考.

1 几何设计与运动学、静力学特性

所有折纸研究的起点都是折痕图设计,清晰折纸结构的运动学和静力学特性,又是开展动力学研究的前提.为此,首先简要介绍折纸的基本定义、假设和分类,随后对常见的折痕设计和折纸结构进行回顾,并讨论折纸超材料的构成方式.本节也将对折纸结构所特有的运动学和静力学特性进行综述,并概要性地介绍折纸结构和折纸超材料的应用前景.

1.1 基本定义、假设和分类

对折纸进行数学描述必须包含等距性和内射性两个条件.等距性(isometry)描述了折纸材料的不可延展性(non-stretchiness),具体指:两点之间沿着纸面的最短距离不会随着折叠改变.内射性(injectivity)描述了折叠过程中纸面的不可自交性(non-selfintersection),具体指:在整个折叠过程中,纸面不能发生自相交.

每一个折纸结构都有其对应的折痕图(crease pattern).折痕图包含的元素有折痕(包括山折痕和谷折痕)、顶点、折面;描述折痕图和折叠过程的常用几何量是扇形角和折叠角.下面给出它们的具体定义.

(1) 折痕(crease):折痕图上的线性要素,折叠围绕其发生.折痕可以不发生折叠(unfolded),部分折叠(partially folded),或完全折叠(fully folded).

(2) 顶点(vertex):两条或多条折痕的相交点.一个顶点的度数(degree)为n,是指有n条折痕相交于该顶点.

(3) 折面(facet):由折痕和(或)边界围成的多边形区域.

(4) 扇形角(sector angle):两条相邻折痕围绕其相交顶点的角度,常表示为 α .

(5) 折叠角(folding angle):折面偏离水平面的角度,常表示为 θ .

(6) 二面角(dihedral angle):两个相邻折面围绕其相连折痕的二面角,常表示为 ρ .

(7) 山折痕(mountain fold):向外折叠的折痕,通常对应负的折叠角.当山折痕被完全折叠时,折叠角为 - 180°.

(8) 谷折痕(valley fold):向内折叠的折痕,通常对应正的折叠角.当谷折痕被完全折叠时,折叠角为180°.

在上述定义的基础上,根据不同的假设,折纸结构可以被描述为不同的数学模型:

(9) 刚性可折折纸(rigidly foldable origami):在折面不发生弯曲和屈曲,折痕和顶点不在折面内移位的情况下,如果折纸结构可以在展开状态(unfolded state)和完全折叠状态(fully-folded state)间连续变化,则称为刚性可折.

(10) 可折平折纸(flat-foldable origami):假设折面厚度为零(可忽略),在折面不发生弯曲、屈曲、自交,且不产生新折痕和新顶点的情况下,如果折纸结构可以被完全折平,则称为可折平.Kawasaki-Justin定理表明,折痕图中一个内部顶点可以被折平的充要条件是围绕该顶点的所有扇形角满足α1-α2+α3-α4+···+αN-1-αN=0,且N为偶数.但需要注意的是,Kawasaki-Justin 定理是某折痕图所对应的折纸结构具有可折平性的必要不充分条件.

(11) 可展平折纸(developable origami):一个处于折叠状态的结构,如果其可以被展开为一张平纸,则称为可展平.数学上,围绕着一个内部顶点的所有扇形角的和为 3 60°,即,则该顶点可以被展平;如果折痕图中所有内部顶点都满足该条件,则基于该折痕图所折的折纸结构具有可展平性.

(12) 厚板折纸(thick origami):考虑折面厚度的折纸.

(13) 曲面折纸(curved origami):假设折面厚度为零(可忽略),折叠过程中折面和折痕可以被弯曲的折纸.

1.2 常见的折痕图设计和折纸结构

折纸为三维结构设计提供了无限可能.在几何上,通过精细设计折痕,二维薄片可以被折叠为复杂的三维形状.例如,通过定制折痕,可以逼近任意常曲率或变曲率的三维表面[46],或任意给定形状的几何多面体[47].在现有的折纸结构和折纸超材料研究中,以下几类折痕图受到广泛关注.

4°顶点折纸(degree-4 vertex origami)是最基本的刚性折纸,它由4 块刚性折面通过相交于一点的4 条折痕连接而成(图3(a)).为保证可展平性,4 条折痕构成的4 个扇形角之和等于 3 60°(α1+α2+α3+α4=360°).在此基础上,如果4 个扇形角满足Kawasaki-Justin 条件(即 α1-α2+α3-α4=0),则该4°顶点折纸具有可折平性[22];如果4 个扇形角满足α1+α4=α2+α3=180°,则该4°顶点折纸有一对折痕共线[48];如果4 个扇形角同时满足α1+α3=α2+α4=180o和α1-α2+α3-α4=0,则4°顶点折纸退化为经典的三浦折纸(Miura-ori)(图3(b))[49].Fang 等[22]发现,三浦折纸仅能实现伸缩变形,可折平4°顶点折纸可以同时实现伸缩变形和面外剪切变形,具有一对共线折痕的4°顶点折纸可以同时实现伸缩变形和面内剪切变形,而一般的4°顶点折纸可以同时实现伸缩、面内剪切、面外剪切和弯曲变形.Yasuda 等[24,50]还在三浦折纸的基础上提出了Tachi-Miura polyhedron (TMP)结构 (图3(d)),其也保持了刚性可折平性.上述这些4°顶点折纸及其堆叠结构在超材料开发方面得到了广泛的关注[23-24,50-51].

水弹(waterbomb)是一种具有更高度数顶点的折痕图,包含8°顶点或6°顶点,均具有刚性可折性.其中,8°顶点waterbomb 折痕图由4 条山折痕和4 条谷折痕交错排列构成(图3(e)),而6°顶点waterbomb 折痕图是由4 条山折痕和2 条谷折痕构成(图3(f))[52].通过周期性排列6°顶点waterbomb单元,可以折叠成著名的“魔力折纸球”(magic origami ball)(图3(f))[17].

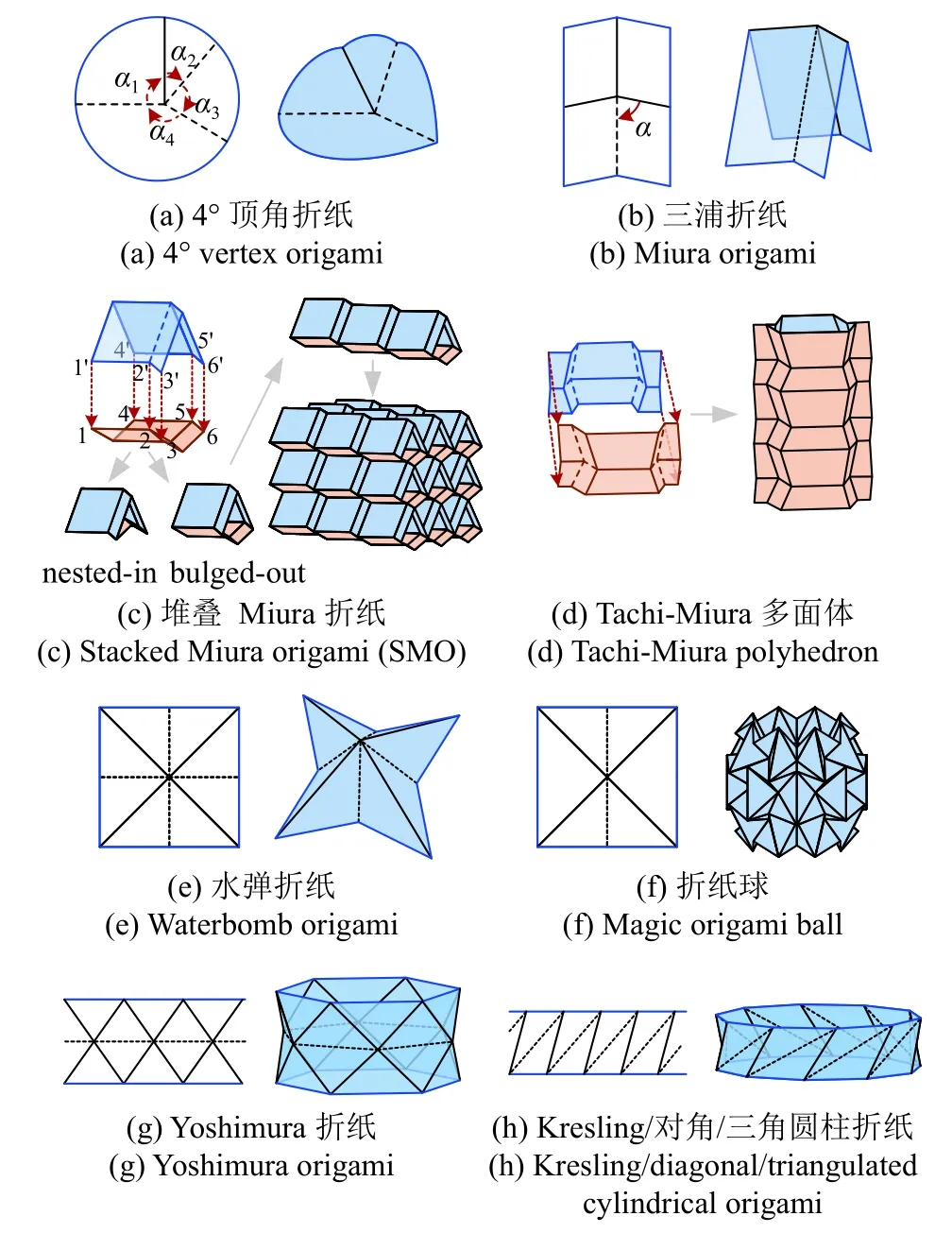
图3 常见的折纸结构的折痕图和三维构型Fig.3 Crease patterns and 3D configurations of classical origami structures

Yoshimura[53]折痕图(有时也命名为钻石折痕图(diamond pattern))同样隶属于6°顶点折痕图,其最早发现于薄壁圆筒在轴向压力下屈曲失稳形成的图案.Yoshimura 折痕图表现为沿对角线折叠的菱形,且对角线的折痕全部为山折痕或谷折痕(图3(g))[54].Yoshimura 折纸属于刚性可折折纸,其同时具有可展平性、可折平性,且具有多个独立的折叠自由度.将Yoshimura 折纸单元在平面两个方向上排布并将两侧的边界重合黏接,可以形成Yoshimura 柱状结构.与Yoshimura 折纸不同,Yoshimura 柱状结构不再保持刚性可折[1],但有望应用于航天可展结构.

与Yoshimura 折纸类似,Kresling 折纸(Kresling origami)(有时也命名为对角折纸(diagonal origami)、三角圆柱折纸(triangulated cylindrical origami)等)[33,55-57]来源于薄壁圆柱受轴向压缩和扭屈时屈曲形成的图案.Kresling 折痕图由平行四边形构成,每个平行四边形的对角线上布置有相同山折痕或谷折痕.将Kresling 折纸单元在平面上排布并将两侧的边界重合粘接,也可以形成Kresling 柱状结构,其也丢失了刚性可折性.在容许折面发生变形的情况下,Kresling 柱状结构在折叠过程中表现出显著的拉压和扭转耦合的变形模式[58].

1.3 折纸超材料构成:平铺和堆叠

将折纸结构作为一个单胞在平面上依照某种平移对称的方式进行平铺(tessellation),可以构成平面折纸薄板,其被广泛用于三明治板材的核心[59].典型的代表包括三浦折纸、waterbomb 折纸[52]、Ron-Resch 折纸[60]等.此外,如图3(f)～ 图3(h)所示,6°顶点waterbomb 折纸、Yoshimura 折纸和Kresling折纸等,都可以进行平面平铺,并通过连接边界折痕形成柱状结构.

进一步地,将相同的平面折纸薄板在另一个维度进行堆叠(stacking),可以构成空间拓扑结构,成为折纸超材料.通过调整几何设计,可以对折纸超材料在3 个主轴方向上几何和力学特性进行调控.最早的堆叠结构案例包括三浦折纸堆叠(stacked miuraori,SMO) 结构[23](图3(c)) 和TMP 堆叠结构[24,50](图3(d)).经过堆叠,SMO 和TMP 超材料依然保持了可折平性和刚性可折性,因此,三浦折纸单胞和TMP 折纸单胞的很多特性在堆叠结构中获得了保留.

将不同的平面折纸薄板进行堆叠需要额外的约束条件,以确保在刚性折叠过程中,两块薄板不会发生脱离.例如,在连接两个不同的4°顶点折纸单元时,需要保证相连折痕的长度相同、相关顶点之间的距离始终保持一致,相关折痕之间的角度也始终保持一致.通过考虑这些刚性折叠几何约束,可以得到堆叠不同平面折纸薄板需要满足的几何相容性条件[22].具体地,两个不同的三浦折纸单元也可以堆叠成为一个SMO 结构,其可以呈现出内嵌(nested-in)和外凸(bulged-out)两种拓扑不同的构型,且依然保持刚性可折性和可折平性[23,27](图3(c)).可折平的4°顶点折纸和具有一对共线折痕的4°顶点折纸也可以进行堆叠,但是一般的4°顶点折纸无法进行堆叠操作[22].

1.4 运动学和静力学特性

由于无穷的几何可设计性和丰富的折叠变形,折纸结构和折纸超材料可以呈现出许多有异于传统组分材料和工程结构的运动学和静力学特性.折纸结构的运动学超常规特性包括尺度无关特性、单自由度或有限自由度作动特性等;静力学超常规特性包括负泊松比、多稳态、可编程刚度等.这些特性极大地丰富了折纸结构和折纸超材料在各个领域的应用.下面简要介绍现有研究报道的折纸结构和折纸超材料的超常规运动学和静力学特性,及其可能的应用场景.

(1) 轻量化.折纸结构可以由质量很轻的二维材料(例如:纸张和塑料薄板等)通过折叠制成,这样可以在保证刚度等性能的前提下显著地降低结构的整体质量[61-63].基于这样的优点,折纸结构被成功应用于航天可展部件,既降低了发射质量,又可以实现巨大的展开面积[64-65].轻量化的折纸结构也为减少机器人自重、降低机器人开发成本提供了全新的方案,学者们提出了许多具有可重构、自折叠特性的机器人设计,并已成为未来机器人发展的重要方向之一[6,16-17,66].

(2) 尺度无关性.折纸结构和折纸超材料的尺度无关性是指:将折痕图放大到结构尺寸或缩小到微纳级别大小时由折叠所诱发的特性不会改变.因此,理论上,折纸结构和折纸超材料可以在不改变运动学性能的前提下应用到不同尺度的结构中,小至纳米尺度的 DNA Origami[67],大至超大型空间可展开结构[15,64].然而,在实际应用中,折纸结构和折纸超材料的尺寸会受到加工和惯性的影响:微纳级别的折纸超材料对制作工艺和保持可折叠性提出了很高挑战[10,68],而过大的折纸结构则会影响刚性可折性,在折叠过程中将无法忽略折面惯性对折叠运动的影响[69].

(3) 单自由度或有限自由度作动特性.单自由度作动特性是指仅需改变一个折叠角,就可以将刚性折纸结构从初始的展开状态转变到完全折叠状态.对于单自由度折纸结构而言,尽管存在多个折叠角,但是这些角度间存在着运动学约束,仅有一个折叠角是独立的.因此,单自由度折纸结构从展开状态到完全折叠状态之间只存在一条折展路径,可以仅用一个折叠角予以描述.三浦折纸及相关的SMO 堆叠结构就属于单自由度作动类型[23].有限自由度作动特性是指可以通过调整多个折叠角改变刚性折纸结构的构型,这些折叠角的变化相互独立.因此,需要有限多个折叠角才可以描述有限自由度折纸结构在折叠过程中的构型变化[70].针对一般性的刚性折叠折纸结构,已有相关研究给出了基于邻接矩阵(adjacent matrix)计算自由度数目的方法[71].6° 水弹折纸结构就属于有限自由度作动类型,其具有3 个折叠自由度,但通过施加对称性约束,其自由度可以缩减到一个[52].事实上,折纸结构虽然常具有复杂的几何形状,但却可以通过单自由度或有限自由度作动实现构型切换,极大地减少了对驱动器数目的需求,降低了驱控的难度.

(4) 负泊松比.泊松比定义为负的材料横向应变与纵向应变之比,因此负泊松比表示材料受纵向拉伸时在横向方向上发生膨胀,而在纵向受压缩时在横向发生收缩.对于刚性折纸结构而言,其负泊松比特性可以通过运动学分析精确得到.三浦折纸结构具有负的面内泊松比特性:在平面内沿一个方向拉伸三浦折纸结构,其在与之垂直的方向上也发生伸长(图4(a)).这样的负泊松比特性使得三浦折叠可以用于调控微孔结构中弹性波的传播[72].有趣的是,在面外弯曲时三浦折纸将呈现出马鞍形,即正的面外泊松比,这种正、负泊松比组合的情况在其他材料中比较少见[23,73].此外,TMP 堆叠结构在折叠过程中,还将发生泊松比符号的切换[24].值得指出的是,负泊松比在折纸结构中普遍存在,如4°顶点折纸单元[22]和水弹折纸结构[74]等.

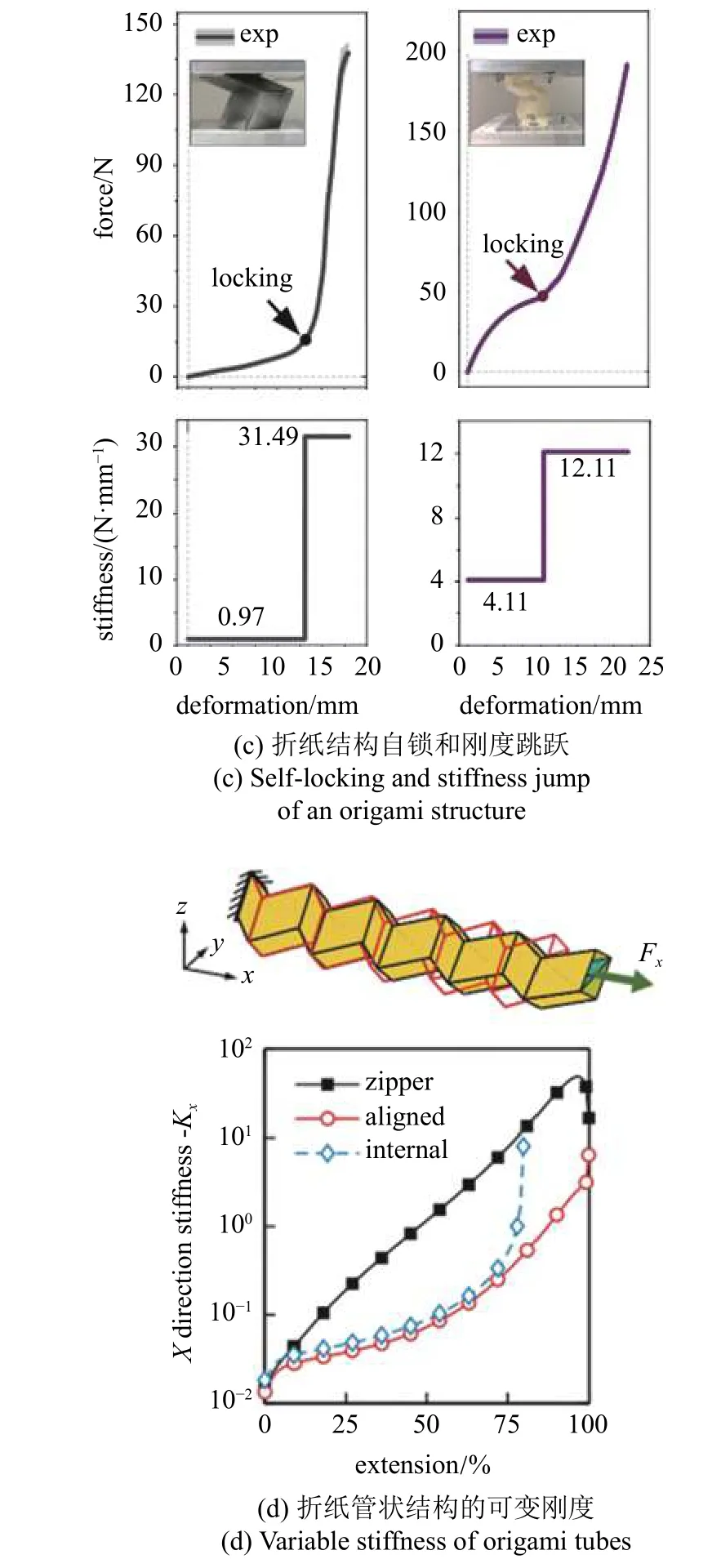
图4 折纸结构的超常规运动学和静力学特性[23,28,30,83]Fig.4 Extraordinary kinematic and mechanical properties of origami structures[23,28,30,83]

(5) 多稳态.多稳态是指结构具有两个及以上的稳定平衡位置,在外力作用下,结构可以在这些位置间切换,而撤去外力时,结构可以稳定地维持在这些位置.这样的特性使得多稳态结构能够适应于不同的环境而无需持续的外部能量输入.多稳态结构有着多种多样的应用,例如传感、振动控制和能量收集等[75].折纸结构的多稳态来源于刚性折叠时折叠角之间的几何一对多关系(即刚性折叠多稳态折纸结构),或非刚性折叠时折面变形和折痕扭转共同导致的非线性几何关系(即非刚性折叠多稳态折纸结构).多稳态折纸结构可以诱发许多独特的力学行为.例如,将折纸结构从一个稳定构型切换至另一个稳定构型,当通过它们之间的不稳定构型时,将呈现出快速的“突弹跳跃(snap-through)”响应,并对应于负的切线刚度(tangent stiffness).

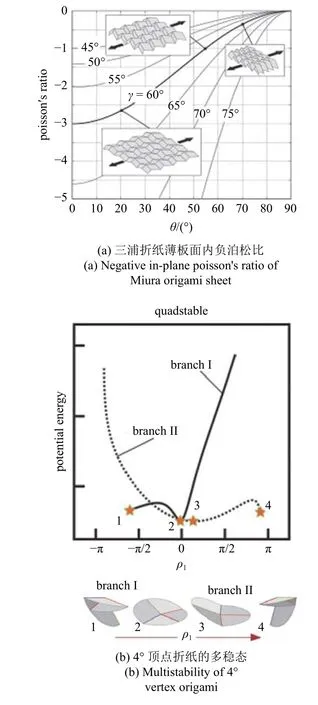
计算折纸结构的弹性势能随折叠过程的演化是分析折纸结构是否具有多稳态特性的重要方法.具体地,刚性折纸结构的势能仅来源于折痕弹性变形(即将折痕认为是具有扭转刚度的理想铰链),利用折叠角之间的一对多映射关系,可以得到多个势能局部极小值,分别对应于多个稳定构型.例如,通过精心设计,4°顶点折纸结构可以实现2～5 个稳定的平衡构型[28](图4(b)).6°顶点水弹折纸[76]和8°顶点leaf-out 折纸结构[77]也可以是多稳态的.堆叠也是形成刚性折叠多稳态折纸结构的有效方式.例如,通过调控几何设计和无应力初始构型,TMP堆叠结构可以呈现出双稳态特性[24];通过调控构成SMO 结构的两个三浦折纸单胞的折痕刚度,SMO结构也将具有双稳态[27];通过改变堆叠方式,SMO变体结构还有可能在弯曲和倾斜方向上呈现出多稳态[29].

非刚性折纸结构的势能来源于折面和折痕的弹性变形.相比于刚性折纸结构,非刚性折纸结构折面的弹性变形将不可忽略,甚至可以从根本上改变折纸结构整体的势能特性.例如,Kresling 柱状折纸结构在轴向受压时,在折面弯曲变形和折痕扭转变形共同作用下,将呈现出独特的压扭耦合双稳态特性[78].基于6°顶点waterbomb 单元开发的折纸球结构也被证实具有三稳态特性[17].此外,square-twist 折纸结构在刚性折叠假设下不具有折叠自由度(即刚性不可折),但通过引入折面的弯曲变形,其“隐藏”的自由度被激活,呈现出了多稳态特性[79].

(6) 自锁和刚度跳跃.“自锁(self-locking)”是指折纸结构在沿着折痕刚性折叠的过程中折面发生接触而不能被进一步折叠,“锁定”在它的最终非平面刚性构型的现象[22,48].自锁特性是4°顶点折纸的常见特征.在4°顶点折纸家族中,只有满足Kawasaki-Justin 条件的一小部分折痕图有可能被折平,而其余绝大多数4°顶点折纸结构都将在刚性折叠过程中发生自锁现象.

在刚性可折折纸的假设下,折面接触后折纸结构进入“锁定”状态,折纸结构刚度将跃升至无穷大.但在实际中,构成折纸结构的材料具有有限的刚度,自锁发生后,由于折面和折痕的弹性变形,折纸结构可以被继续折叠.但是,自锁前后,折纸结构的刚度具有完全不同的来源.自锁之前,折纸结构的刚度主要来源于折痕的扭转刚度;自锁之后,除了折痕的扭转刚度,折面刚度对折纸结构的整体刚度具有重要贡献.这样的刚度来源变化将使得折纸结构在自锁构型前后呈现出显著的刚度差异,形成刚度跳跃[30](图4(c)).自锁和刚度跳跃特性对超材料和自适应结构的开发具有重要意义.例如,可以基于自锁实现折纸超材料的分段刚度本构[30].此外,还有学者基于三浦折纸,提出了一类具有膨胀、双稳定和自锁特性的多孔超材料[80].将折纸结构和形状记忆合金材料耦合,也可以实现自锁[81].折纸结构的自锁特性还被成功应用于可折叠机械臂[16]、可展开空间吊杆结构[82]等.

(7) 刚度可调性和可编程性.折纸结构和折纸超材料可以通过3 种方式实现对刚度的调控.第一种方式中,考虑到折纸结构在不同构型时具有不同的切线刚度,因此可以通过折叠来实现刚度调节.例如,由三浦折纸管状结构和“拉链式”管状结构组合而成的结构,在不同的折叠程度下具有显著不同的切线刚度,表现为不同的特征值(图4(d))[83].SMO 结构在3 个主轴方向具有显著不同的刚度本构,且也与折叠程度密切相关[84].这种基于折叠的大范围刚度可调性,是折纸超材料区别于其他力学超材料的显著优势之一.

另一种刚度调控的方式是利用折纸结构单胞的自锁和多稳态特性实现折纸超材料整体刚度的可编程性.具体地,通过建立折纸结构单胞的构型与数字编码(0,1 等)的关系,可以实现折纸超材料整体刚度的数字化调控.例如,通过调控构成单胞的自锁顺序或稳态构型,可以实现对刚度本构的编程[30,85];通过在线切换构成单胞的稳态构型,可以实现对三浦折纸薄板整体刚度的在线编程[31].

第3 种调控刚度的方式来自于外部作动.例如,通过调节封闭折纸结构内部的气压,可以实现折纸结构形状变换和刚度调控[84].考虑到折纸结构的刚性可折特性,这样的形状变换具有可恢复性,可以用于开发可重复使用的能量收集装置[84,86].磁铁也是调控折纸结构刚度的有效方式.将折叠弹性势能和磁力势能耦合,可以定性或定量地改变折纸结构的本构特性,例如,通过电磁铁实现Kresling 柱状折纸结构在单稳态和多稳态之间的切换[87].在squaretwist 折纸结构中,折面变形程度决定了系统自由度的多少,通过温度调控折面刚度,可以使squaretwist 折纸结构在刚性单稳态和非刚性多稳态间切换,从而实现主动重构[88].

2 动力学建模方法

除了上述运动学和静力学特性,折纸结构和折纸超材料的动力学研究受到越来越多的关注.从研究方法出发,折纸结构和折纸超材料动力学研究可以分为3 类:基于模型的动力学研究、基于有限元的动力学研究和动力学实验研究.这其中,基于模型的动力学研究具有基础性和核心性地位,其计算效率较高,可以用于预测折纸结构和折纸超材料的动力学行为,并为动力学性能优化提供依据.

基于模型的动力学研究的基础是建立准确、可靠、可处理的动力学模型,这需要根据研究目的提取折纸结构和折纸超材料的关键特征,简化一些次要特征.根据建模的主要假设和依据,折纸结构和折纸超材料的动力学建模方法分为:空间桁架等效动力学建模方法、非线性弹簧等效动力学建模方法、基于广义哈密顿原理的等效动力学建模方法和数据驱动动力学建模方法.下面,分别介绍上述方法,并分析所建立的动力学模型的合理性和可处理性.此外,本节也对边界约束和折面接触的处理方法,以及几何、物理参数的辨识方法进行讨论,它们对建立动力学模型具有重要意义.

2.1 空间桁架等效动力学建模

空间桁架等效动力学建模方法对于刚性不可折、部分刚性可折和完全刚性可折的折纸结构和折纸超材料均适用,下面分别介绍.

针对刚性不可折折纸结构和折纸超材料,在建立空间桁架等效动力学模型时,一般遵循如下假设:忽略折面;将折痕等效为可以轴向变形的无质量连杆,并在节点处用铰链连接;结构的上下端面保持刚性.随后,通过建立上下端部面板的惯性张量以及桁架对端部面板施加的力和力矩,可以采用牛顿-欧拉方法建立结构的动力学方程.Kresling 折纸结构是典型的刚性不可折结构,其由水平折痕、垂直折痕和对角折痕组成.基于上述思路并考虑阻尼因素,Kidambi和Wang[33]建立了6 自由度(3 个位移分量pB0/A0,3 个欧拉角 ω) Kresling 折纸结构的空间桁架等效动力学模型(图5(a))

其中,FBi和GBi分别表示桁架对上端面板施加的力矢量和扭矩矢量;mB,R和IB0分别表示上端面板的质量、旋转张量和惯性张量.类似地,Yasuda 和Yang[89]利用线性弹簧替代折痕,也建立了Kresling 折纸结构的空间桁架等效动力学模型.由于忽略了折面的存在,这样的模型无法描述折面的弯曲变形,但桁架连杆长度的变化所引起的等效折面伸缩和剪切变形依然可以用于分析力学响应[26].此外,通过将折痕描述为可以发生伸缩变形的连杆/线性弹簧,桁架结构的势能可以简单地表示为桁架中连杆/线形弹簧长度改变量的函数,极大地简化了分析,易于给出桁架处的作用力和力矩.通过忽略Kresling 折纸结构在轴外的变形,Yasuda 等[39]建立了2 自由度空间桁架等效动力学模型(图5(b)).该模型考虑了不同长度折痕线刚度的差异,并通过扭转弹簧模拟折面绕上下端面的旋转.通过建立Kresling 折纸结构轴向变形和旋转变形间的关系并予以线性化,该2 自由度模型可以被进一步简化为单自由度等效动力学模型.Kidambi 和Wang[33]在研究中指出,他们建立的6 自由度动力学模型在退化情况下与Yasuda 等[39]建立的2 自由度模型等价.

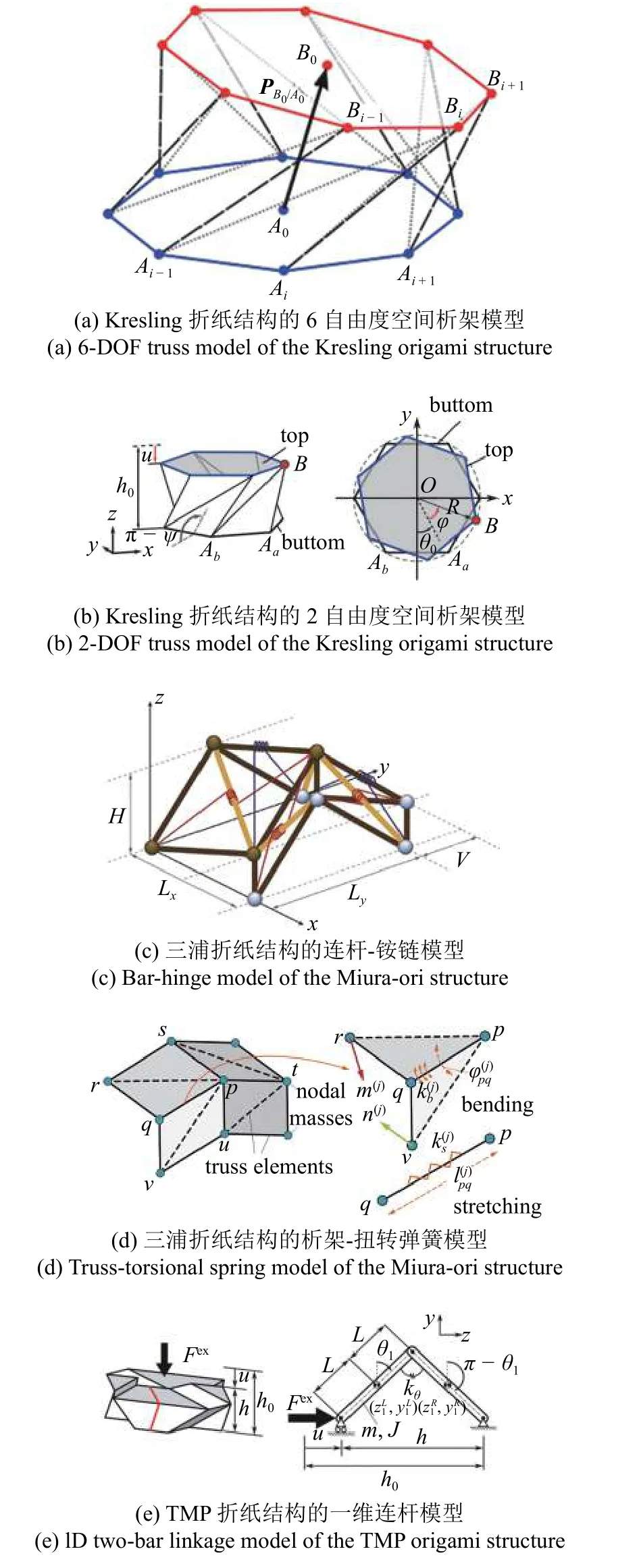
图5 折纸结构和折纸超材料空间桁架等效动力学模型[33,39,90-92]Fig.5 Truss-based equivalent dynamic models of origami structures and origami metamaterials[33,39,90-92]

某些折纸结构理论上具有刚性可折性,但基于不同材料制备的试样在折叠过程中,折面将有可能发生不同程度的弯曲变形,成为部分刚性可折.处理折面弯曲的一种方式是在折面上添加沿对角线的虚拟折痕,将四边形折面拆分为两个三角形折面.针对这样由三角形折面、折痕和虚拟折痕构成的折纸结构,也可以建立相应的空间桁架等效动力学模型.建模的基本假设是:忽略折面;将折面的质量均匀分布到三角形的3 个节点上;将折痕等效为无质量的桁架连杆,但连杆上布置有扭转弹簧,连杆在节点处用铰链连接.于是,折纸结构的折叠运动可以被描述为由绕连杆的旋转铰链构成的柔性机构.为了区分绕折痕的折叠和折面的弯曲,对应于折痕和虚拟折痕的连杆被赋予不同的扭转刚度.随后,通过考虑节点质量、节点位移和节点处所受合力,可以建立结构的动力学模型.针对三浦折纸结构和鸡蛋盒(eggbox)折纸结构,Pratapa 等[90]构造了对应的空间桁架(图5(c)),通过建立质量矩阵并利用虚功原理建立刚度矩阵,得到了三浦折纸和鸡蛋盒折纸的空间桁架等效动力学模型.Bhovad 和Li[91]根据等效节点质量mp以及作用在节点上的连杆拉伸力、折痕/面弯曲力、等效阻尼力、外部驱动力和重力mp g(图5(d)),基于牛顿第二定律给出了关于节点p的位移的等效动力学方程

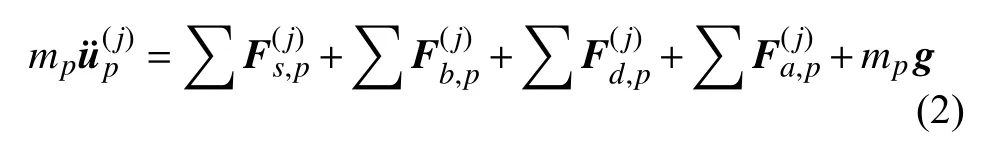
其中上标 (j) 表示数值计算中第j个时间步.

针对刚性可折折纸结构,空间桁架模型可以进一步简化为只容许一维运动的连杆结构,以抓住结构的刚性可折和单自由度作动特性.Yasuda 等[92-93]通过这样的思路对TMP 结构进行了等效动力学建模.建模的基本假设是:将TMP 折纸结构的整体折叠运动等效为两个代表性折面的折叠运动,并进一步用两根刚性杆(图5(e)中红色线段)的相对折叠运动等效折面的折叠运动;两根连杆用铰链和扭转弹簧相连;折纸单胞的质量均匀分布于两根连杆上;一根连杆与地面铰接,另一根连杆通过滚子关节支撑,以确保该双连杆系统只能发生一个方向的平移.通过分析刚性连杆的运动,第j个TMP 单元的动力学方程可以通过虚功原理给出[92]

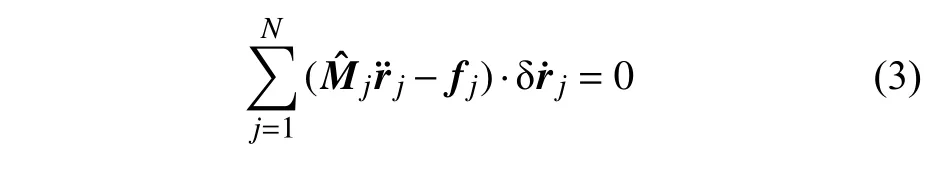
其中,rj是由两根连杆的质心坐标及方向角形成的的向量,和fj分别表示对应的质量矩阵和外力矢量.在此基础上,Yasuda 等[92,94]还建立了由N个TMP 单元构成的超材料的动力学模型

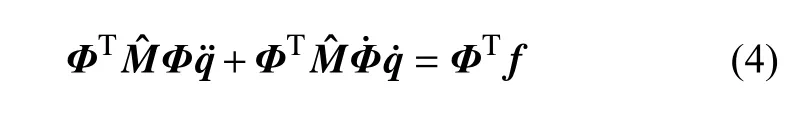
其中,Φ 表示坐标变换矩阵,Mˆ和f分别表示整体质量矩阵和力矢量,q则表示广义坐标矢量.

上述空间桁架等效动力学建模方法针对刚性不可折、部分刚性可折和完全刚性可折折纸结构,采用了不同的建模假设.从动力学模型的合理性和可处理性角度来看:

(1)通过把非刚性折叠行为等效为连杆的拉伸/压缩行为,极大地简化了折纸结构的动力学建模过程,获得的动力学模型也具有较高的可处理性.但是,在折叠过程中,空间桁架模型忽略了折纸结构的一些关键特性,如折面的惯性、折面的弯曲变形、折面绕折痕的刚性旋转等.

(2)针对部分刚性可折的折纸结构,绕折痕的折叠行为和折面弯曲行为被等效描述为连杆的拉伸压缩、折面绕折痕和虚拟折痕的旋转.这样建立的模型考虑了折面的惯性,绕折痕的旋转和折面的弯曲也可以通过赋予折痕和虚拟折痕不同的扭转刚度予以区分.但是,这样的建模方法需要将折面三角化,在折纸结构模型较为复杂时将导致可处理性变差.

(3)针对完全刚性可折的折纸结构,一维连杆模型准确地体现了刚性折叠和单自由度作动特性,模型简单且计算效率较高,特别适用于小振幅的波动力学问题.但这样的动力学模型对折面的惯性简化过度,完全丢弃了折纸结构的大变形折叠特征,无法分析大振幅动力学行为.

2.2 非线性弹簧等效动力学建模

非线性弹簧等效动力学建模方法仅仅考虑折纸结构和折纸超材料沿着折叠变形方向的直线平移运动,将折纸结构和折纸超材料整体等效为非线性弹簧-阻尼模型或非线性弹簧-质量-阻尼模型.前者忽略了折纸结构和折纸超材料自身的质量,但需要在模型中考虑添加在端部的集中载荷;而后者则将折纸结构和折纸超材料的质量等效为单元间的集中质量.通过能量法或准静态拉压测试,可以得到等效非线性弹簧的本构关系,并进而基于牛顿第二定律建立动力学模型.目前,已有SMO 单胞结构、SMO 超材料、流体折纸(fluidic origami)结构和TMP 超材料等建立了非线性弹簧等效动力学模型.

通过能量法推导等效非线性弹簧的本构关系常用于刚性可折折纸结构.对于刚性可折折纸结构和折纸超材料,折痕被看作是具有扭转刚度的理想铰链,通过计算所有折痕处储存的弹性势能即可以得到折纸结构整体的势能.将势能(P)对折叠变形的位移(H)求导,可以导出折纸结构的力-位移本构关系

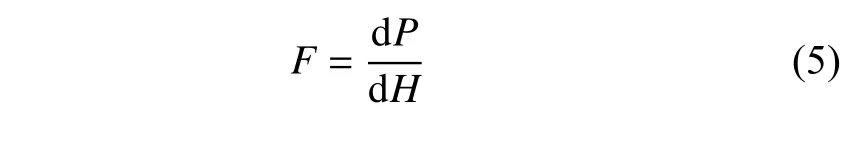
Sadeghi 等[95]将TMP 折纸结构等效为非线性弹簧和阻尼,并利用虚功原理分析了TMP 管状结构沿长度方向的反作用力.邱海等[96]将 SMO 双胞串联结构建模为等效弹簧-阻尼模型,并附加两个集中质量,然后使用12 次多项式拟合了由能量法得到的非线性弹簧本构关系.Zhang 等[38]用两种不同的15 阶多项式拟合了SMO 单胞在内嵌和外凸两种不同拓扑构型下的力-位移本构关系(表示为Fin和Fout,多项式系数为 αj和βj(j=1,2,···,15),并把SMO 单胞在长度、宽度和高度方向分别周期堆叠后形成的SMO 超材料建模为串联非线性弹簧-质量振子(图6(a));例如,在高度方向(具有双稳态)上,如果将连续的3 个外凸-外凸-内嵌SMO 单胞作为一个基本单元,则第p个基本单元的动力学方程可以表示为

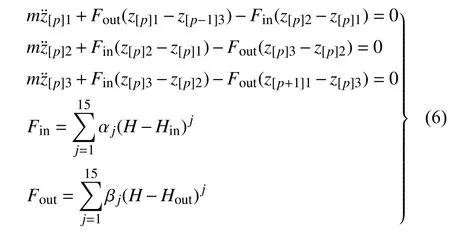
其中,z[p]i,i=1,2,3 表示第p个基本单元中第i个SMO 单胞的位移,Hin和Hout是SMO 单胞在两种不同拓扑稳定构型下的长度.

除了折痕处储存的弹性势能,外界物理场和作动因素也会影响折纸结构整体的势能.Fang 等[87]将耦合有磁铁的SMO 单胞等效为无质量非线性弹簧和粘性阻尼,基于理论模型计算了包含磁势能和折痕弹性势能的本构关系,并通过27 阶多项式对理论本构关系进行了拟合(图6(b)).流体折纸结构可以通过调控内部流体压力改变本构,Sadeghi 和Li[18]将其等效为非线性弹簧和阻尼,并用多项式拟合了在内部压力作用下的力-位移本构关系.

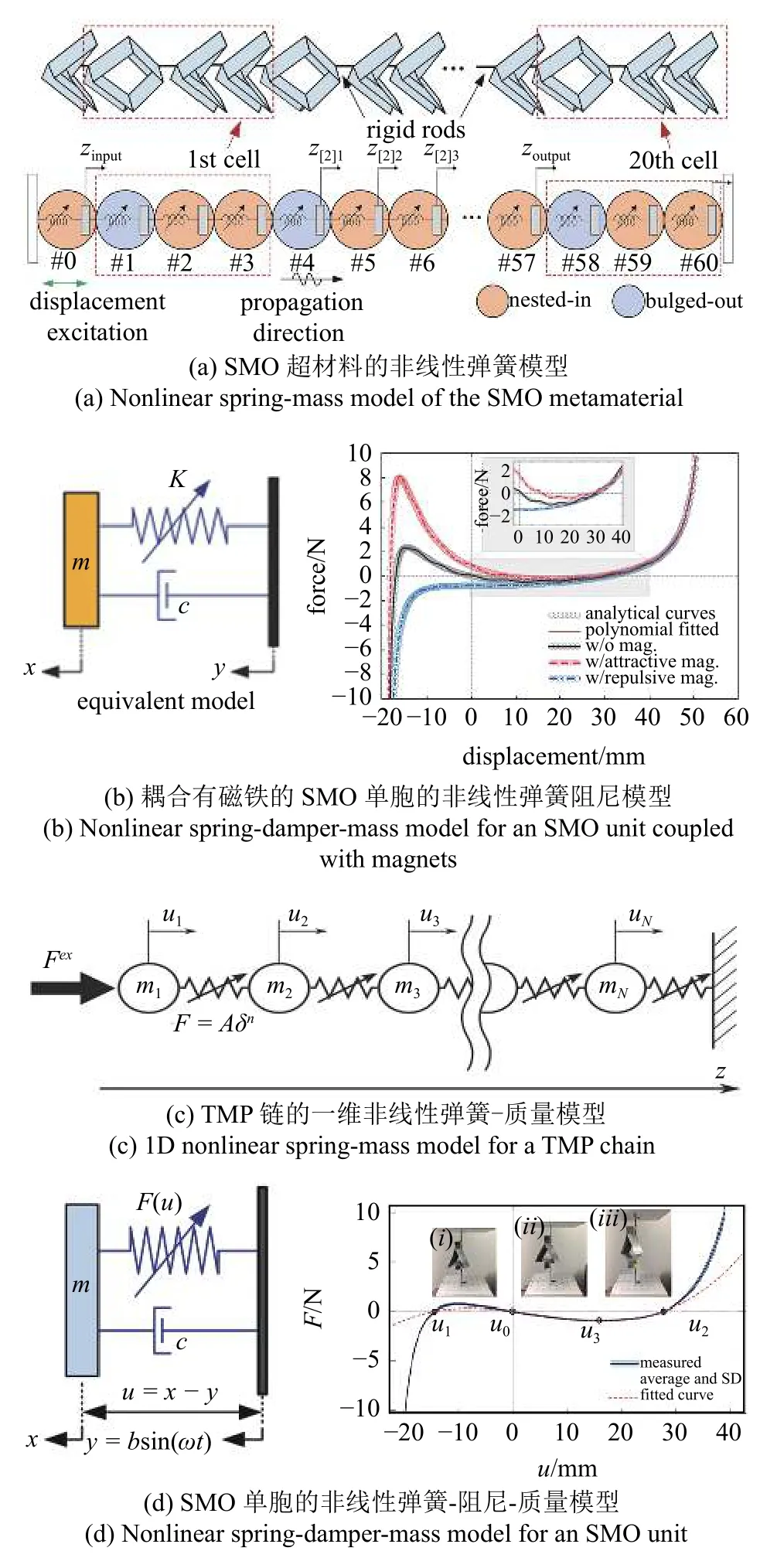
图6 折纸结构和折纸超材料的非线性弹簧等效动力学模型[27,38,87,92]Fig.6 Nonlinear spring-based equivalent dynamic models of origami structures and origami metamaterials[27,38,87,92]

此外,2.1 节中介绍的TMP 结构的一维等效连杆模型也可以被进一步简化描述为非线性弹簧-质量振子.Yasuda 等[92]将TMP 结构的的力-位移本构关系(具有应变软化特征)通过多项式进行拟合(图6(c)),并施加一个拉伸方向的位移偏移量,以使非线性弹簧-质量振子模型在受压和受拉区域都可以近似双连杆模型的力-位移本构关系.为了分析在平衡位置附近的小振幅运动,还可以在小位移假设下对力-位移本构关系进行线性化,从而建立单个TMP结构和多个TMP 链式结构的线性弹簧-质量振子等效模型.

准静态拉压实验可以直接得到折纸结构和折纸超材料的力-位移本构关系.Fang 等[27]对SMO 单胞进行了简谐位移激励,发现SMO 单胞的动力学响应具有明显的二次和三次谐波项,意味着SMO 单胞结构包含显著的平方和立方非线性特征.为此,可以对由准静态拉压实验得到的力-位移本构关系进行三阶多项式拟合,并确保SMO 单胞的两个稳定平衡位置(z=z1和z=z2) 和一个不稳定平衡位置(z=z0)对应于力-位移本构本构关系的3 个零点(图6(d)),由此得到SMO 单胞的非线性弹簧-阻尼-质量振子动力学模型

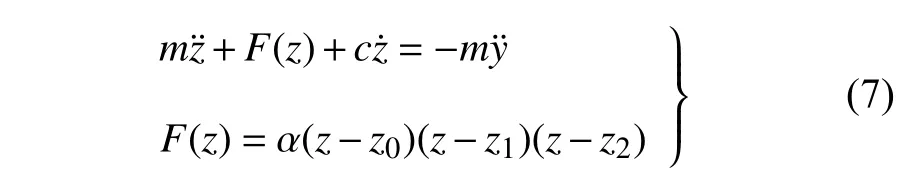
其中y表示位移激励.Fang 等[30]还在折纸结构中发现了由自锁行为引起的分段刚度本构,提出了具有双向限位功能的自锁折纸超材料,并通过组合弹簧模型来近似自锁折纸超材料的分段刚度本构,其中,组合弹簧的刚度通过准静态实验或有限元仿真得到.

上述非线性弹簧等效动力学建模方法可以准确地描述折纸结构和折纸超材料整体的力-位移本构关系,包括分段线性刚度、多稳态和磁弹耦合等复杂情况.因此,通过非线性弹簧等效动力学建模方法得到的动力学方程一般有着较为简单的形式.此外,使用多项式函数对折纸结构和折纸超材料的非线性本构关系进行拟合有助于实现计算精度与计算效率的平衡.但是,非线性弹簧等效动力学建模方法也存在着较大的局限性.首先,非线性弹簧等效模型通常忽略折纸结构和折纸超材料整体的惯性,或将其等效为额外的集中质量;这样的模型无法描述折纸结构和折纸超材料自身质量无法忽略时的动力学行为.其次,通过多项式拟合本构关系时,多项式的阶数会对准确性与可处理性产生显著影响,如何选择多项式的阶数是一个值得探讨的问题;过高的阶数将显著降低模型的可处理性,而过低的阶数将无法抓取本构关系的重要特征.再次,非线性弹簧等效模型通常无法处理存在不理想因素时的情况,例如由于不理想折痕引起的非折叠方向的振动.

2.3 基于广义哈密顿原理的动力学建模

基于广义哈密顿原理对折纸结构和折纸超材料进行建模是一种更具普遍性和准确性的动力学建模方法.在该方法中,首先需要推导结构的动能、势能和非保守力所做虚功,随后代入广义哈密顿原理,得到一般形式的拉格朗日方程

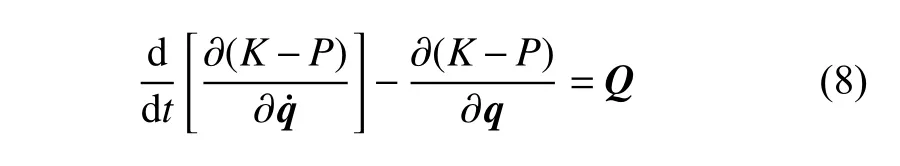
其中,K和P分别表示折纸结构和折纸超材料的动能与势能,Q和q则分别为非保守广义力矢量与广义坐标矢量.折纸结构和折纸超材料的动能、势能获取方法主要有两类:模型简化方法和基于刚性折叠的运动学分析方法,下面分别介绍.最后,对文献中出现的不同类型广义力进行介绍.

模型简化方法是指将折纸结构和折纸超材料进行一定程度的简化,以便于求得动能与势能,大致可以细分为以下3 种.

第1 种是对折纸结构和折纸超材料的动能计算进行简化.例如,将折面质量等效为折面质心处的集中质量,由此简化折面动能的推导.Sadeghi 和Li[74]在对waterbomb 折纸结构建模时,将三角形折面的质量简化为折面质心处的集中质量,根据各个折面相对于中心顶点的关系得到了各个折面质心的速度,由此求得了waterbomb 折纸结构整体的动能等效表达式 (图7(a)).

第2 种是对折纸结构和折纸超材料的势能计算进行简化.例如将折痕折叠和折面弯曲等效为具有不同刚度的扭转弹簧,从而将连续体的弹性势能计算简化为理想弹簧的势能计算.Soleimani 等[97]用6 个线性和扭转弹簧来限制两块相连的四边形折面在6 个自由度上的相对位移,并进而对其折叠行为进行建模描述.该系统的势能包括折面弯曲储存的应变能(),折面边界弹簧引起的势能(),以及模拟折叠行为的耦合弹簧所引起的势能(Pf)(图7(b))

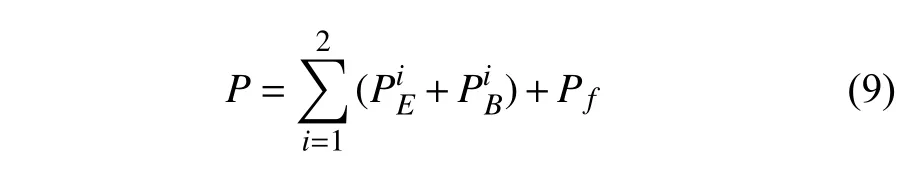
具体地,折面边界弹簧势能被等效为3 个线性弹簧和2 个扭转弹簧(图7(b)右下角),而折面的折叠行为则处理为3 个线性弹簧和3 个扭转弹簧(图7(b)右上角).此外,折纸结构中的热力学作动也可以被等效建模为弹性势能.例如,Fonseca 和Savi[98]研究了含有折纸轮结构的机器人的非线性动力学行为,并用2,4,6 阶多项式近似拟合了形状记忆合金(SMA)弹簧(其为折纸轮的作动器)的势能

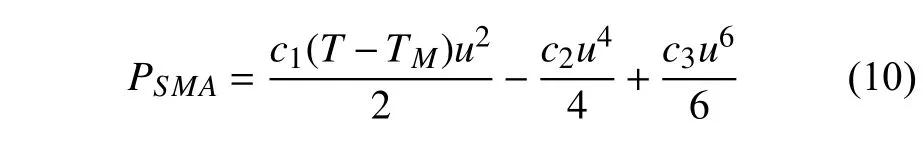
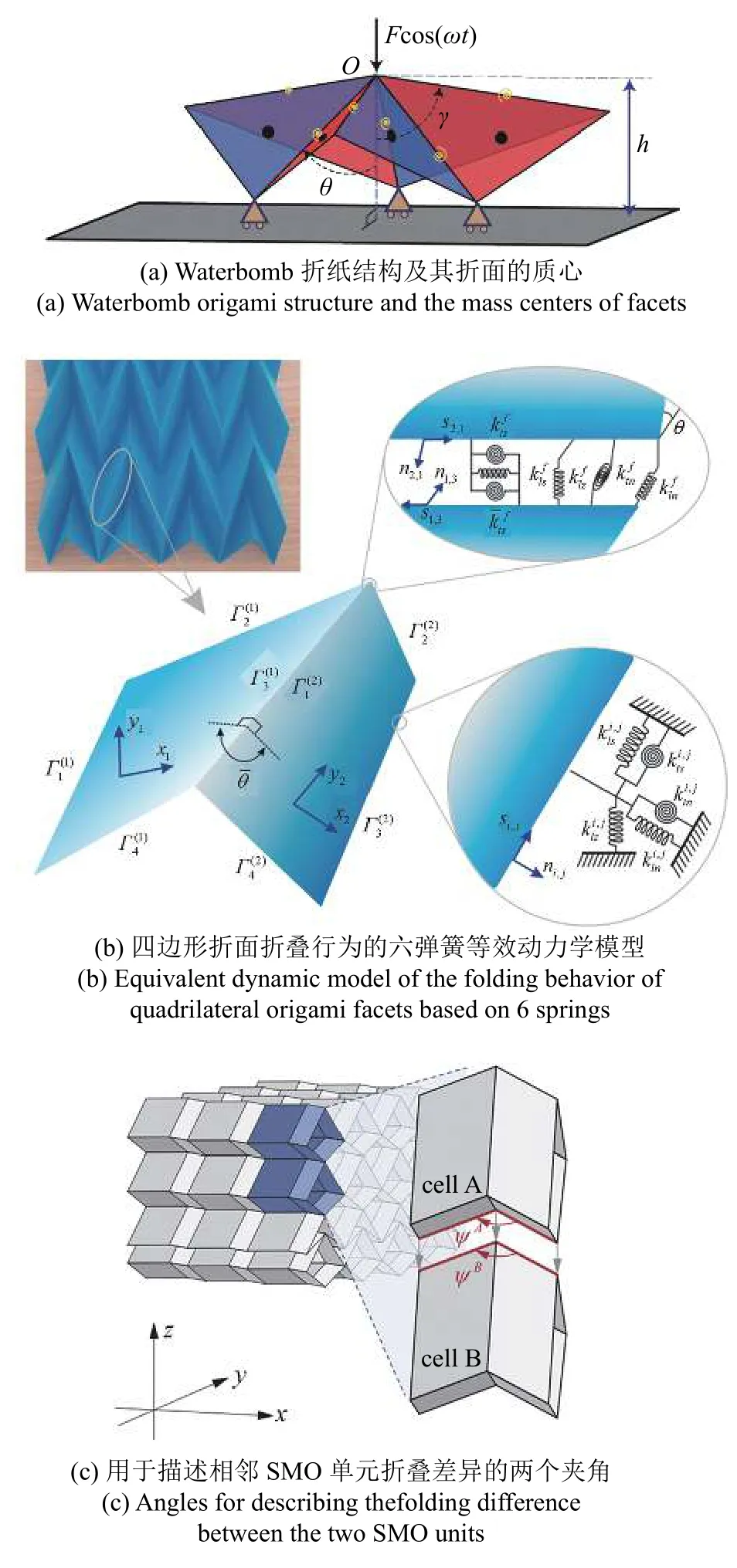
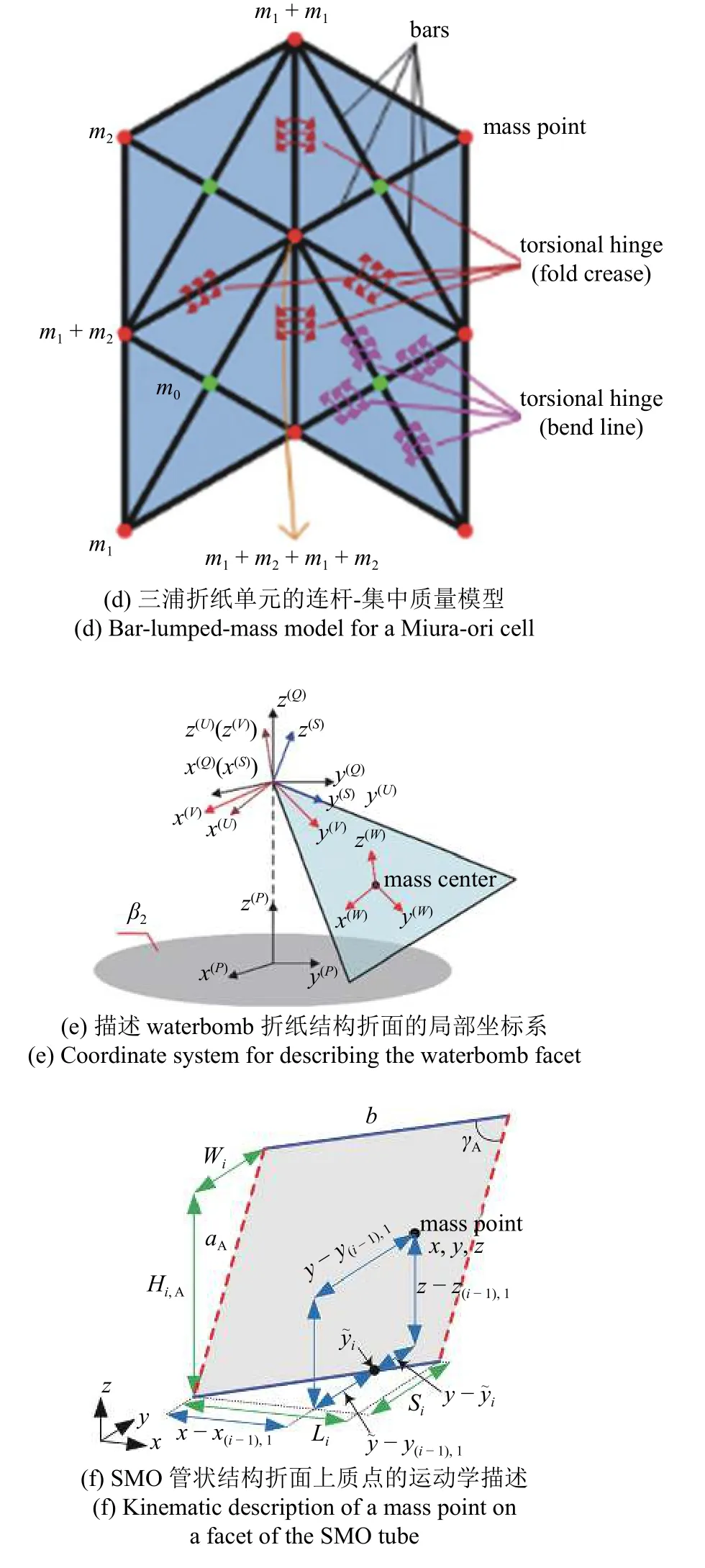
图7 折纸结构和折纸超材料基于广义哈密顿原理等效建模研究进展[34,74,97,99-100,104]Fig.7 Equivalent dynamic modeling of origami structures and origami metamaterials based on generalized Hamilton principle[34,74,97,99-100,104]

其中,ci(i=1,2,3)为本构模型参数,TM表示临界温度,马氏体在低于这个温度时是稳定的,u表示SMA弹簧的长度变化量.针对非刚性可折三浦折纸管状结构展开时不同半单胞间的折叠差异,Wu 等[34]在相邻半单胞间附加了扭转弹簧,并用附加弹性势能来建模和约束相邻半单胞间的折叠差异.Zhou 等[99]也用类似的附加扭转弹簧建模了SMO 双胞串联结构中单胞间的非理想连接,并通过附加弹性势能来约束两个SMO 单胞的折叠差异(折叠差异通过两个角度描述(图7(c))).Liu 和Felton[36]针对由柔性铰链和塑料折面构成的折纸结构,发现其势能可以通过计算从静平衡构型准静态地切换到不稳定平衡点所做的功得到,即对准静态实验中的力矩积分得到.

第3 种是直接对折纸结构和折纸超材料进行结构简化,以方便动能和势能的计算.最常见的是对折面通过有限单元法进行建模,将折面的分布质量等效为节点处的集中质量,或通过折面的形函数得到集中质量矩阵.Xia 等[100]将连续的三浦折纸薄板简化为连杆-节点集中质量系统(图7(d)),其系统动能可以表示为节点动能之和,系统势能包括折面弯曲变形和折痕弯曲的能量,及连杆伸缩的弹性势能.Zhang 等[101]将四边形单元离散为两个三角形单元,在三角形折面区域V上对形状函数(几何描述)进行积分后得到三角形折面单元的一致质量矩阵

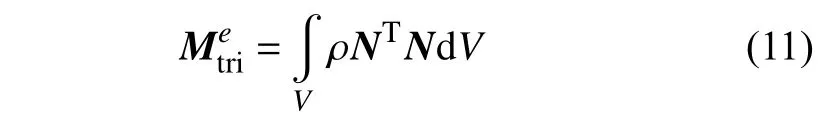
其中 ρ 为体积密度,N为形状函数矩阵.将两个三角形单元的矩阵元素进行组合,得到四边形单元的一致质量矩阵

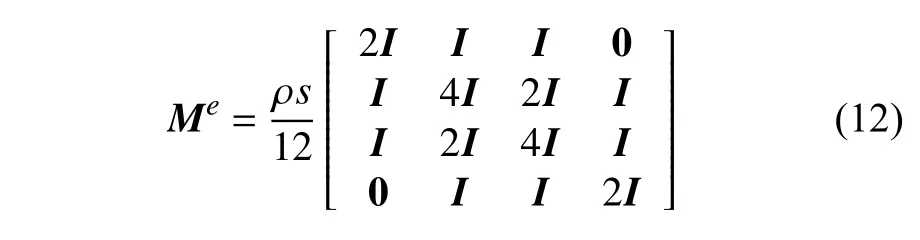
其中I为三维单位矩阵,s表示三角形单元的面积.Yuan 等[102]基于绝对节点坐标法(absolute nodal coordinate formulation,ANCF)将折纸薄膜结构离散为三角形单元,并通过单元的形状函数矩阵求得三角形单元的动能,在此基础上通过连接矩阵推导出结构整体动能.除了上述基于有限单元思想的简化方法,也有研究直接将折纸结构和折纸超材料简化为桁架和非线性弹簧组合的系统,Han 等[103]建立了基于三浦折纸管状结构的准零刚度隔振器,并将其等效为由四根连杆、一个水平弹簧和一个垂直弹簧构成的系统,极大地简化了动能和势能的计算.

基于刚性折叠的运动学分析方法是指在刚性可折假设下,通过刚体运动学明确折面上各点的速度,随后通过柯尼希定理或积分方法推导折纸结构或折纸超材料整体的动能;折纸结构和折纸超材料的势能包括折痕折叠弹性势能和重力势能,它们可以在刚性可折假设下基于上述简化分析方法求得.

具体地,折面的动能可以进一步分为平动动能和转动动能,因此,动能的推导问题转变为折面质心速度、折面旋转角速度和转动惯量的计算问题.例如,通过在折面质心上建立质心坐标系(图7(e)) 并根据运动学关系得到折面的质心速度、绕质心轴的角速度和旋转张量,可以计算折面的动能[104-105].当折纸结构的折面顶点被固定时,折面的运动表现为定点转动的形式;Liu 和Felton[36]在建立三浦折纸结构构型切换的动力学模型时考虑了这种情形.折面速度积分方法首先将折面上任意一点的坐标用顶点坐标表示,随后对时间求导得到该点的速度,并以此速度代表该点所在的微元的速度.通过计算微元的动能并对整个折面积分可以得到整个折面的动能.Wu 等[34]基于SMO 管状结构刚性折面上任意一点与顶点的位移关系(图7(f)),确定了该点沿3 个主方向的速度分量,并通过折面速度积分法得到了折面和SMO 管状结构整体的动能.类似地,Soleimani等[97]在每个折面上建立局部坐标系,并推导折面上每个质点在局部坐标系中的位移分量,进而求出该质点处的速度分量并对折面积分求得整个结构的动能(图7(b)).

在刚性可折假设下,折痕折叠时的弹性势能是折纸结构整体势能的重要组成部分,其可以被描述为折痕处扭转刚度和相对折叠二面角的函数.基于此,研究者们给出了waterbomb 折纸结构[74,104]和三浦折纸结构[34]的弹性势能.折纸结构在构型变化时折面的质心相对高度会发生变化,从而改变重力势能,但当前折纸结构动力学研究中对重力势能的关注较少.例如,在计算waterbomb 折纸结构[74,104]和折纸轮结构[98]的势能时,质心改变引起的重力势能改变都被计算在内,但其对动力学行为的影响较小.

在基于广义哈密顿原理建立折纸结构和折纸超材料的动力学模型时,非保守力对应的广义力必须予以考虑.目前主要关注的是阻尼力、主动力和接触力所对应的广义力,他们通常都通过虚功原理得到.在动力学研究中,折纸结构和折纸超材料中的阻尼因素不可忽略.当前,主要考虑的阻尼类型有线性阻尼[74]、黏性阻尼[34,98,100,104-105]和比例阻尼[102].在动力学研究中,主动力也起着至关重要的作用,用以给系统提供外激励或者改变初始构型.常见的外激励形式包括:简谐激励[74,104-105]、冲击力[98]和位移激励[98,100]等.此外,为了限制系统的响应在一定范围内,有些研究还给出了对应于几何约束的广义力[101,104-105].为了防止具有柔性的折面在运动过程中相互接触,Yuan 等[102]还利用混合接触模型定义了广义接触力.

基于广义哈密顿原理的动力学建模方法充分考虑了折纸结构和折纸超材料本身的惯性、折面绕折痕的折叠运动、折面弹性形变等.模型推导中,根据折纸结构和折纸超材料是否保持刚性可折性,动能和势能可以基于不同方法推导(例如刚体运动学关系、模型等效简化、折面速度积分、实验本构关系积分和有限元单元法等),得到的动力学模型较为完备.但是,相较于桁架等效模型和非线性弹簧等效模型,基于广义哈密顿原理的动力学建模过程较为繁琐,模型自由度明显提高,造成计算复杂度较高,模型可处理性较低.此外,对于柔性特别显著的折纸结构和折纸超材料,其变形与刚性折叠迥异,需要通过有限单元离散来实现建模;为了保证计算精度,通常离散的单元数目众多,方法本质上已成为了有限元方法.

2.4 约束及接触的处理

在对折纸结构和折纸超材料进行动力学建模时,折纸结构和折纸超材料的边界连接方式、相邻单胞间的几何和运动学约束、非刚性折纸或非零厚度折纸结构中折面接触与碰撞等问题常带来许多挑战,值得深入研究.下面将对这几个方向的研究进展作简要介绍,其中部分工作虽未涉及动力学建模,但这些关于折纸结构边界约束、折面厚度、折面接触的研究对折纸结构精细化动力学建模具有重要的借鉴意义.

折纸结构和折纸超材料边界处的约束方式对整体性能具有较大影响.Terada 等[106]对不同边界条件下三浦折纸结构的实验结果与有限元结果进行了比较.实验中,将三浦折纸的短边夹紧会增大靠近约束部位的单胞的刚度(图8(a));约束在几何上的不对称性,也会对横向方向刚度产生较大影响,因此有必要考虑约束的方向性.注意到,在上述非线性弹簧等效动力学建模中,通常仅考虑折纸结构沿一个方向的运动,因此边界条件较为简单,主要包含固定边界、位移激励边界以及自由边界3 种类型.而在空间桁架等效动力学建模和基于广义哈密顿原理的动力学建模中,限制某些顶点的全部或部分方向的位移则是普遍的处理方法.

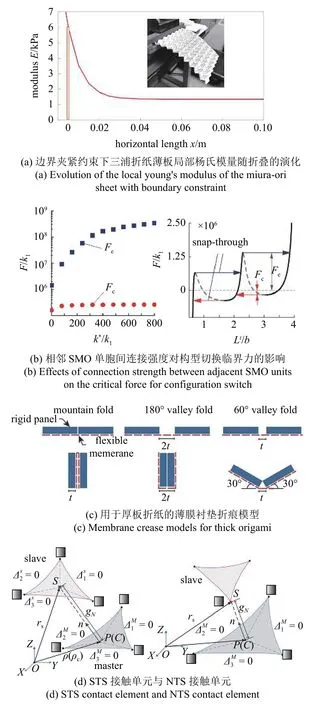
图8 折纸结构和折纸超材料约束及折面接触处理[102,106-107,110]Fig.8 Constraints and contact of origami structures and origami metamaterials

尽管刚性可折假设极大地简化了折纸结构和折纸超材料的建模与分析,但是折纸结构和折纸超材料中常包含一些非刚性成分,并受到了越来越多研究者的关注.虚拟折痕就是一个最典型的例子,其将折面的弹性弯曲变形等效为两个折面绕虚拟折痕的折叠变形.其次,不同折纸单胞之间的连接也常具有非刚性特征,并会对结构性能产生较大影响.Fang等[107]研究了两个SMO 单胞在高度方向上堆叠形成的双胞串联结构,用额外的弹性势能来表征两个单胞间共享折痕处连接方式的差异(图7(c)).对于理想折痕连接,附加弹簧的刚度为无穷大,两单胞SMO 串联结构退化为单自由度系统;对于非理想折痕连接,附加弹簧的刚度为有限值;而对于刚性杆连接,附加弹簧的刚度为零,两个单元的折叠变形完全独立.研究表明,不同的附加弹簧刚度会显著地改变双胞串联结构的力-位移本构关系,甚至实现机械二极管效应(图8(b)).Wu 等[34]在考虑SMO 管状结构不同单胞之间折叠差异时也用了类似的附加弹性势能进行等效建模.Zhang 等[108]在研究折纸关节的非刚性连接问题时,基于板理论和扭转弹簧模型预测了半刚性连接折纸关节的折叠刚度和弯曲变形.

在实际应用中,折纸材料的厚度是一个无法回避的问题.一方面,折纸结构和折纸超材料自身的质量会随着材料厚度的增加而增大.另一方面,较低的折面厚度会引起折面柔度增加,加大折面弯曲和扭转的可能性.此外,有厚度的折面在折叠到一定程度时也会引起折叠性能的改变,如折叠自锁的发生条件会改变,引起分段刚度本构[30]等.当前已有不少研究开始关注材料的厚度对折纸结构和折纸超材料折叠变形和力学性能的影响,即厚板折纸研究.Yellowhorse 等[63]使用有限元模型对由厚板材料制成的刚性可折折纸管进行了结构优化,讨论了在不同长度下的对称和非对称管的力学性能.Zhang 和Kawaguchi[109]利用广义逆理论研究了重力与折纸厚度共存时厚板折纸结构的折叠运动.Zirbel 等[110]提出了两种方式来实现厚板折纸的物理建模,即允许折面沿对角线折叠或在折痕处添加指定宽度的薄膜衬垫(图8(c));基于此建立的模型已在厚板可展开太阳帆板中予以验证.Chen 等[111]提出了一种刚性厚板折纸结构的综合运动学模型,通过空间连杆运动模拟刚性折纸的球面连杆机构,再现了与零厚度折纸相同的折叠运动.在计算方面,Zhu 和Filipov[112]提出可以通过调整折纸结构数值计算模型中的参数来模拟折面厚度对接触的影响.

在真实折叠运动和折叠的数值仿真中,折面都有可能与其他折面或顶点发生接触与碰撞,主要原因有以下几方面.首先,在实验中,某些折纸结构不具有可折平性,它们的刚性折叠过程会由于折面与折面的接触而终止[30];由于材料厚度不可忽略,厚板折纸在折叠过程中的接触与碰撞现象更容易发生,例如发生折面边界与其他折面的接触,两个折面边界的接触等.其次,折纸结构的可折叠范围有限,而数值计算模型无法避免这种情形,从而导致数值模型中折面与折面发生接触与穿透,致使计算结果发散.针对这种情况,直接的解决办法是在动力学方程中增加边界约束力,如前文提到的与边界约束相关的广义力[104-105]用以限制系统响应范围,表示为一个等效的弹性弹簧刚度,或者用运动学约束对限制进行表示,并写成运动学约束的广义力形式[101].折纸结构和折纸超材料折叠过程中顶点与折面或折面与折面之间的接触碰撞问题也已经引起了研究者的关注.Zhu 和Filipov[112]提出了一种在广义折纸框架下模拟面板接触的数值方法,用以分析接触的发生和接触引发的力学特性.具体地,在摩擦力不显著的条件下,假设接触力是保守的并对应于一个势能函数;因此,当顶点与折面非常接近时,接触势能将导致一个很大的内力矢量和刚度矩阵;距离接近零时,内力矢量和刚度矩阵都将趋向于无穷大,以防止穿透发生.Yuan 等[102]在研究折纸空间薄膜结构展开的动力学建模问题时,采用了基于绝对节点坐标法的三角膜单元来解决薄膜几何非线性和折叠问题,并提出将折面-折面(surface-to-surface,STS)接触单元和节点-折面(node-to-surface,NTS) 接触单元(图8(d)) 混合使用以提高接触碰撞问题的计算精度.

2.5 几何与物理参数辨识

尽管已经提出许多折纸结构和折纸超材料的动力学建模方法,但注意到,这些建立的模型大多只能定性地预测和分析折纸结构的动力学行为,无法定量地与实验结果进行比照.部分原因在于,折纸结构和折纸超材料的动力学行为与其物理参数和几何参数息息相关.对刚性折叠而言,其力与位移本构关系主要与折痕的扭转度刚度和相邻折面间处于无应力状态时的角度相关[107,113];而对非刚性折叠来说,还涉及到折面材料的拉伸、弯曲和剪切以及折痕的弯曲模量[83,114].遗憾的是,这些参数往往很难通过简单的测量精确得到.没有这些参数的准确信息,获得精确的折纸结构和折纸超材料力学特性描述和动力学行为预测将变得十分困难.因此,识别折纸结构和折纸超材料的几何和物理参数对于静、动力学研究都具有重要意义.下面,对常见动力学参数辨识方法在折纸结构和折纸超材料上的适用性进行分析,并对已有的折纸结构和折纸超材料动力学参数辨识研究进行综述.

折纸结构和折纸超材料常具有大变形和强几何非线性等特征,会诱发复杂的动力学行为,给动力学参数辨识带来困难.以刚性可折的双稳态SMO 结构为例,实验中观察到了包括小振幅阱内振荡、大振幅阱间稳态响应和大振幅阱间混沌振荡响应等[27].在相同的激励条件下,双稳态SMO 结构有可能在不同初始条件下收敛到不同的稳态响应.这样的初始条件敏感性会加重现有的基于初值迭代的辨识方法的计算负担[115-116].另一方面,折纸结构和折纸超材料常具有全局强几何非线性,有可能诱发全局混沌响应,而动力学测量会不可避免地涉及噪声,这使得在辨识过程中难以分离噪声和混沌信号.一些传统的非线性系统时域辨识方法依赖于离散数据和他们的高阶导数来建立回归矩阵[117],然后通过最小二乘方法,可以很方便地求解得到最优辨识参数.研究指出,在采样时间趋于零的情况下,利用差分算子可以将连续时间系统等价为离散时间系统,这使得前者也能像后者一样拥有良好的回归形式,取得高效的辨识结果[118].但是注意到该算法需要不断对离散测量数据进行数值差分,将不可避免地导致噪声放大,从而造成辨识结果偏差.由此,学者们提出了一系列降噪[119-121]和消除偏差[122]的方法,但考虑到双稳态SMO 结构对噪声敏感且可以呈现混沌响应,简单的滤波处理不再适用,需要考虑系统动力学行为来适当地分离噪声和混沌数据,但这往往会显著提高计算量.

避免数值差分引起的噪声可以采用基函数辨识方法来解决.对测量数据的拟合或对拟合函数进行求导可以代替数值差分操作.基函数的选取对求导十分关键,对拟合精度过高的要求会导致求导时发生高频低幅振荡.通常而言对于周期数据,傅里叶基函数[123-124]比较合适;而对于任意形式的数据,B 样条曲线[125-126]或者小波基函数[127]较常用.除了基函数的形式,基函数的个数也直接影响辨识结果:越多的基函数个数能更好地逼近测试数据,但也同时逼近了测量噪声,因此在求导运算中也更容易放大噪声;而基函数个数较少则有可能丢失数据的一些关键特征[128].由此,学者们提出了逐步变量选择和变量修剪方法[129],用来确定合理的基函数个数.也有研究通过迭代的方式来修正过拟合的数据[125],这和滤波的效果较为相似.粗糙度惩罚也是解决该问题的常用方法之一[128],通过对拟合过程施加惩罚项,过拟合的粗糙特性将被削减,由此拟合函数将更加光滑,从而避免差分引起的噪声问题.然而,惩罚程度如何选取又是一个需要解决的问题,常用的方式包括广义交叉验证[130],但会不可避免地带来额外的计算量.

为平衡计算复杂度与辨识精度,针对双稳态SMO 结构所具有的强非线性、初始条件和测量噪声敏感性等辨识难题,Liu 等[131]通过在时域内应用B 样条伽辽金有限元方法,提出了一种新的适用于全局强非线性折纸结构的参数辨识方法.该方法仍然采用B 样条基函数构造全局解,但通过伽辽金弱解形式和分部积分消除了对拟合函数直接求导的操作.因此,该方法既不放大测量噪声,又不增加计算量,具有适用范围广、效率高、鲁棒性好等优点.该方法成功辨识了SMO 结构处于无应力状态时的折叠角、折痕刚度和阻尼系数等几何与物理参数,识别了SMO 结构的双稳态本构(图9(a)),使得定量预测强非线性动力学响应成为可能.

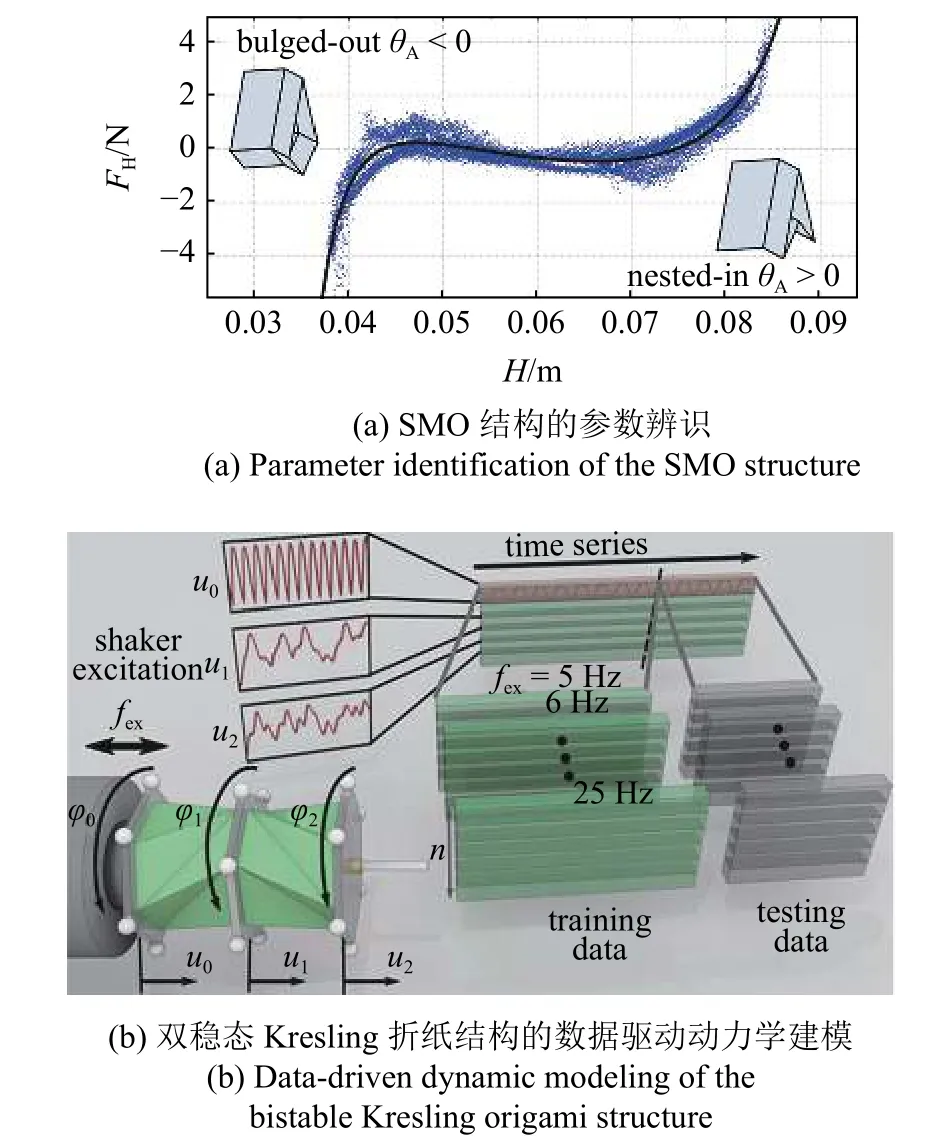
图9 折纸结构和折纸超材料的参数辨识和数据驱动动力学建模[131,140-141]Fig.9 Parameter identification and data-driven dynamic modeling of origami structures and origami metamaterials[131,140-141]

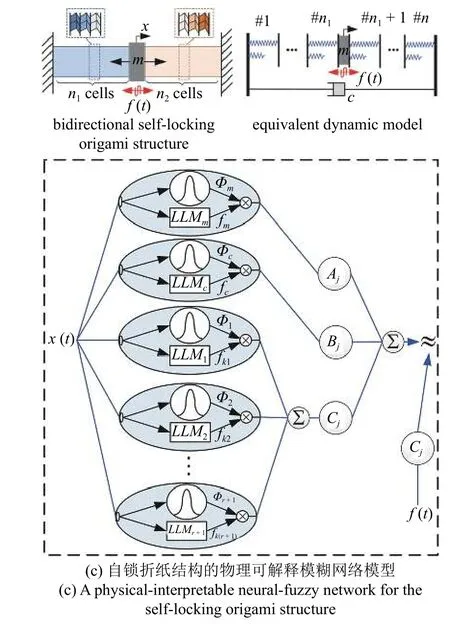
图9 折纸结构和折纸超材料的参数辨识和数据驱动动力学建模[131,140-141] (续)Fig.9 Parameter identification and data-driven dynamic modeling of origami structures and origami metamaterials[131,140-141] (continued)

当然,对于参数辨识,并没有一种“一刀切”的方法.对于其他具有不同超常规特性的折纸结构和折纸超材料的几何与物理参数辨识,仍需要定制相应的辨识方法.这方面的研究还处于初始阶段,亟待发展.

2.6 基于数据驱动的动力学建模方法

基于模型的折纸结构和折纸超材料参数辨识方法依赖于预先给定的理论模型,然后基于实验数据识别几何和物理参数.这样得到的模型具有强可解释性、易于开展参数分析等优点.但是,许多折纸结构具有复杂的几何构型和变形模式,例如非刚性折纸的折叠变形模式尚不清晰,就难以给出第一性原理模型(反应物理规律的模型).其次,折纸超材料往往由数目众多的单胞构成,对每个单胞进行第一性原理建模将使模型过于复杂化,难以处理.再次,折纸结构和折纸超材料的大变形和几何非线性特征容易诱发强非线性多稳态和非光滑刚度跳跃等特性,对传统参数辨识方法也提出了巨大挑战.为避免繁琐的理论建模和复杂的参数辨识方法构建,以数据驱动的方式建立折纸结构的等效动力学模型逐渐得到关注.

数据驱动建模不同于依赖物理定律的第一性原理理论建模,它直接通过数据来建立等效力学模型.近年来,随着数据科学和机器学习方法的飞速发展,可以借助它们来更好地理解复杂数据,并基于完备的模型库提取最简模型形式.当前,数据驱动的静力学建模方法已经取得了重要进展,但从大数据中提取动力学模型的研究才刚起步,并受到了广泛关注.

基于数据的动力学建模方法可以追溯到开普勒和牛顿时期.应用大量精确观测的行星运行数据,开普勒建立了数据驱动的行星运行模型,即著名的椭圆轨道模型.近年来,基于观测数据提取非线性动力学模型的方法取得了一定突破,Bongard 和Lipson[132]以及Schmidt 和Lipson[133]利用符号回归[134]来发现非线性微分方程形式,同时平衡了模型复杂度、测量数目和模型精度之间的矛盾.但是,符号回归计算代价昂贵,并不适用于高维模型,且十分容易过拟合.Brunton 等[135-136]应用稀疏回归方法重构了混沌洛伦兹系统、绕障涡流方程和参数化系统的动力学模型,证明了该方法对常微分方程、偏微分方程、分岔和流形等问题的有效性.

人工神经网络(ANN)[137-138]模拟人脑神经元的运行方式,可以对复杂的输入输出数据进行学习处理,近年来成为人工智能领域的研究热点.神经网络十分适合用于建立复杂非线性系统的等效模型[139].Yasuda 等[140]利用准静态递归神经网络建立了双稳态Kresling 折纸结构的数据驱动动力学模型,并成功预测了结构的混沌响应(图9(b)).该方法不需要对非刚性可折的Kresling 折纸结构进行理论建模,而直接通过数据驱动的方式建立模型并预测动力学响应;另一方面,通过对网络隐藏层的分析,该方法可以用来理解所建立的数据驱动模型对不同类型信号的处理过程.

另一方面,类似人类的推理过程,模糊逻辑以一种可解释性的方式来表现模糊和不精确信息.神经网络和模糊逻辑的混合使用综合了ANN 的“学习”和“普遍逼近”的优点以及模糊逻辑的“可解释”的优点,有希望用于建立具有可解释性的数据驱动动力学模型.针对具有非光滑分段刚度本构的自锁折纸结构[30],Liu 等[141]基于分段线性假设,构建了一个物理可解释的模糊神经网络来关联自锁折纸结构的激励和动力学响应数据.该方法所构造的神经网络模型参数和实际自锁折纸结构参数一一对应,具有较强的物理可解释性:神经元数目与自锁折纸结构刚度本构的分段数目相关联,局部线性模型的系数与刚度本构的参数相关联,有效性函数与非光滑点的位置相关联 (图9(c)).

折纸结构和折纸超材料的数据驱动动力学建模是近年来新兴的研究领域,目前还处于个例分析阶段,更加通用的建模方法还有待研究.

3 动力学分析与实验测试

折纸结构和折纸超材料的动力学研究方法主要包括:基于模型的动力学分析方法、有限元计算方法和动力学实验方法.对折纸结构和折纸超材料进行动力学分析与测试是为了揭示由折叠诱发的动力学特性,进而为折纸结构的设计与优化提供依据.本节对上述3 个方面的研究进展进行综述.

3.1 基于模型的动力学分析

第2 节建立的动力学方程通常具有常微分方程(组)(ODEs)或微分代数方程(组)(DAEs)的形式,因而可以基于各种解析与数值方法进行定性分析和定量求解.例如Han 等[104]在考虑waterbomb 折纸结构在平衡位置附近的小振动时,对动力学方程进行了泰勒级数展开与线性化处理.Zhang 等[101]通过定义非线性残差及泰勒展开,利用Newton-Raphson迭代法对三浦折纸结构进行了线性化.研究频率成分相关问题时,Yasuda 等[94]利用二维快速傅里叶变换(FFT)分析了Kresling 折纸超材料作为波传播媒介时波数与频率的关系,Fang 等[27]应用FFT 分析了双稳态SMO 结构动力学响应主频率分量的位移传递率.在数值求解方法方面,除了广泛使用的各种类型ODE 求解器,一些不常见的数值求解方法也得到了应用.例如,在处理空间可折叠薄膜的展开问题时,变步长广义-α算法被用来求解带有约束的多体系统,其动力学方程形式为微分指数为3 的DAEs[102];Soleimani 等[97]将折纸和剪纸结构中折痕折叠描述为偏微分方程组(PDEs),广义微分求积法(GDQ)可以基于函数值在整个域的指定节点上的加权线性组合来近似导数,被用来数值求解耦合偏微分方程组.

就研究内容而言,折纸结构和折纸超材料动力学研究主要关注固有频率与特征值、稳态动力学和瞬态动力学3 个方面.下面分别介绍进展.折纸结构和折纸超材料在稳定平衡构型处的固有频率是重要的动力学特征.Sadeghi 和Li[74]利用频闪采样研究了waterbomb 折纸结构在两个稳定平衡构型附近的阱内共振频率(图10(a)).邱海和方虹斌等[96]研究了SMO 双胞串联结构在4 个稳定构型处的固有频率特征.此外也有研究关注折纸结构在参数改变或构型改变时动力学特性的变化,如Han 等[104]在对多稳态waterbomb 折纸结构的动力学方程进行线性化处理的基础上,考虑了稳定构型附近的小振幅振动问题,分析了固有频率及平衡点的分岔问题;Xia等[100]通过对三浦折纸薄板进行特征值分析,明确了固有频率随展开过程的变化.

折纸结构和折纸超材料的稳态动力学响应主要分为3 类:第1 类是简谐位移激励下的强迫响应,一般用位移传递率(输出与输入信号的均方根(RMS)值之比)来表示.折纸结构和折纸超材料的稳态响应可以通过不同方法进行求解,例如Han 等[103]在预测三浦折纸管状结构准零刚度隔振器的动态性能时使用的泰勒级数逼近非线性项和平均法;Yasuda等[94]在求解TMP 单胞频响关系时的射击法(shooting method)等;Fang 等[27]在分析SMO 单胞、SMO 双胞串联结构[96]、耦合有磁铁的SMO 单胞[87](图10(b))的频响关系时采用的离散频率扫描方法等.第2 类则是折纸结构和折纸超材料在外激励下的非线性动力学行为,包括稳定性、分岔和混沌等.例如,Rodrigues 等[105]和Han 等[104]研究了waterbomb 折纸结构在热场和机械激励下的复杂非线性动力学行为;邱海等[96]对SMO 双胞串联结构进行了吸引盆分析,研究了初始条件对动力学行为的影响,并用吸引盆稳定性 (basin stability)指标来衡量不同激励幅值下结构动力学特性的演变.第3 类是色散分析,包括波在SMO 超材料中的带隙特征和超传递行为[38],TMP 折纸超材料中波数与频率的关系[94](图10(c))等.

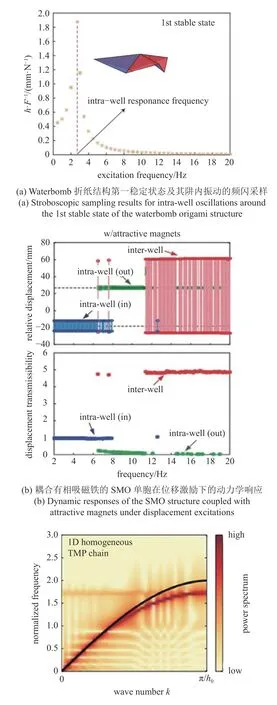
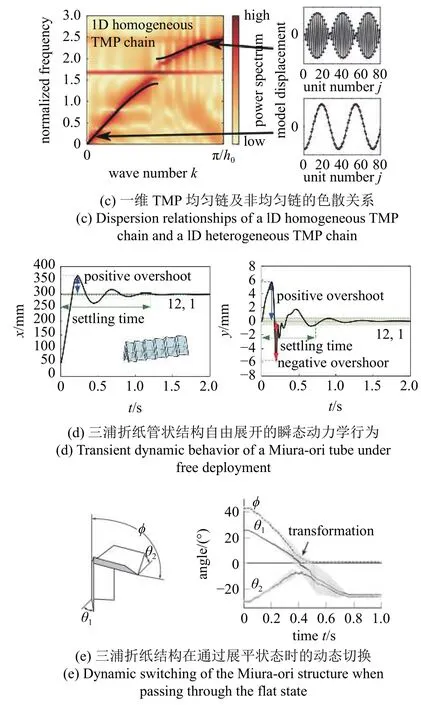
图10 基于模型的折纸结构动力学分析方法[34,36,74,87,94]Fig.10 Model-based dynamic analysis methods of origami structures[34,36,74,87,94]

折纸结构和折纸超材料的瞬态动力学响应包括在冲击力下的瞬态动力学行为、自由展开和受控展开的瞬态动力学行为、构型动态切换行为,以及自由衰减振动响应四种类型.冲击力下的瞬态动力学主要研究冲击波在折纸结构和折纸超材料中的传播速度与衰减.例如,不同幅度冲击力下TMP 折纸超材料中压缩应变波和拉伸应变波的传播[92],TMP 折纸链式结构中稀疏波的存在性和稳定性[92],以及Kresling 折纸超材料在压缩冲击下不同单元的应变[89]等.折纸结构和折纸超材料的展开动力学研究分为自由展开和受控展开.自由展开是指折纸结构在一端受到约束,而另一端在约束释放后的自由展开行为.吴海平和方虹斌等研究了三浦折纸管状结构在自由展开过程中由非刚性折叠诱发的轴向和横向方向上的瞬态动力学行为[34](图10(d));Kidambi 和Wang[33]研究了Kresling 折纸结构在轴向和离轴方向自由展开时的瞬态动力学响应.受控展开是指折纸结构在一端受到约束,另一端在指定速度下的展开行为.Zhang 等[101]研究了可折叠板结构从折叠状态到完全展开状态的整个动态展开过程.展开的瞬态动力学行为常关注以下指标:展开的稳定时间(settling time)和超调量(overshoot)[34]、节点之间的偏差长度[100]、von Mises 应力分布[102]等.

构型动态切换是指折纸结构和折纸超材料在动态过程中越过能障,发生稳态构型切换的行为,如在不同的阱内共振频率下waterbomb 折纸结构在不同稳态构型间的快速跳跃[74],三浦折纸结构通过展平状态时的动态切换[36](图10(e)).折纸结构和折纸超材料的自由衰减振动通常由外界扰动、非稳定初始条件、平衡位置改变所诱发,例如热载荷下折纸支架结构的自由振动响应[105],不同初始条件下waterbomb 折纸结构的有阻尼自由振动[104],以及在外部微扰动下含有折纸轮的机器人系统的瞬态动力学行为[98].

3.2 有限元计算

对于真实的折纸结构和折纸超材料,尤其是当刚性可折性不满足时,折面和折痕的弹性变形将不可忽略,他们的折叠行为也非常复杂,这使得基于运动学和力学原理的建模变得较为困难.基于非线性弹簧和空间桁架的等效动力学模型虽然为动力学分析提供了一定的可行性,但是这些模型无法精确描述折纸结构和折纸超材料的真实折叠行为,更无法对折面和折痕的应变和应力分布等做出刻画.面对这一挑战性难题,采用有限元软件(例如Abaqus 和ANSYS)对折纸结构和折纸超材料进行建模和分析并与实验结果进行比对成为一种可行选择[142-144].在建立有限元模型时,常采用的单元类型为:杆单元、4 顶点/3 顶点壳单元和四面体实体单元.如采用杆单元时,通常将折纸结构视为空间桁架进行分析,例如Cai 等[78]和Chen 等[145]分别利用Abaqus 建立了Kresling 折纸结构和三浦折纸结构的杆单元有限元模型并分析在折叠过程中各杆的受力情况(图11(a)).基于杆单元的有限元模型虽然较为简单,但无法体现折纸结构的面内变形情况,因此学者们开始采用壳单元和实体单元进行建模.例如,Yang 等[146]和Song 等[147]建立了多种管状折纸结构的壳单元有限元模型并分析了它们的受压和吸能特性,建模中不对折痕作额外处理而仅设置初始折叠角度;Du 等[143]和Hu 等[148]分别对曲线折痕折纸结构和三浦折纸结构建立了壳单元模型(图11(b)),并将折痕建模为带刚度的弹性铰,进而研究了折纸结构在折叠时产生的恢复力.对于实体单元有限元模型,一般是直接将折纸结构的CAD 模型导入有限元软件后利用四面体实体单元进行网格划分.例如Fang 等[30]建立了自锁折纸结构的实体单元有限元模型(图11(c)),其中折痕处的材料厚度小于折面的厚度,因此结构可以在给定载荷下沿着预先设计好的折痕进行折叠,并分析由于折面接触导致的自锁所引起的刚度跳跃行为.Sane 等[149]建立了三浦折纸管状结构的实体单元有限元模型,并对折痕做了相似的消减厚度的处理,而后分析了内部充气气压对结构整体变形率的影响.

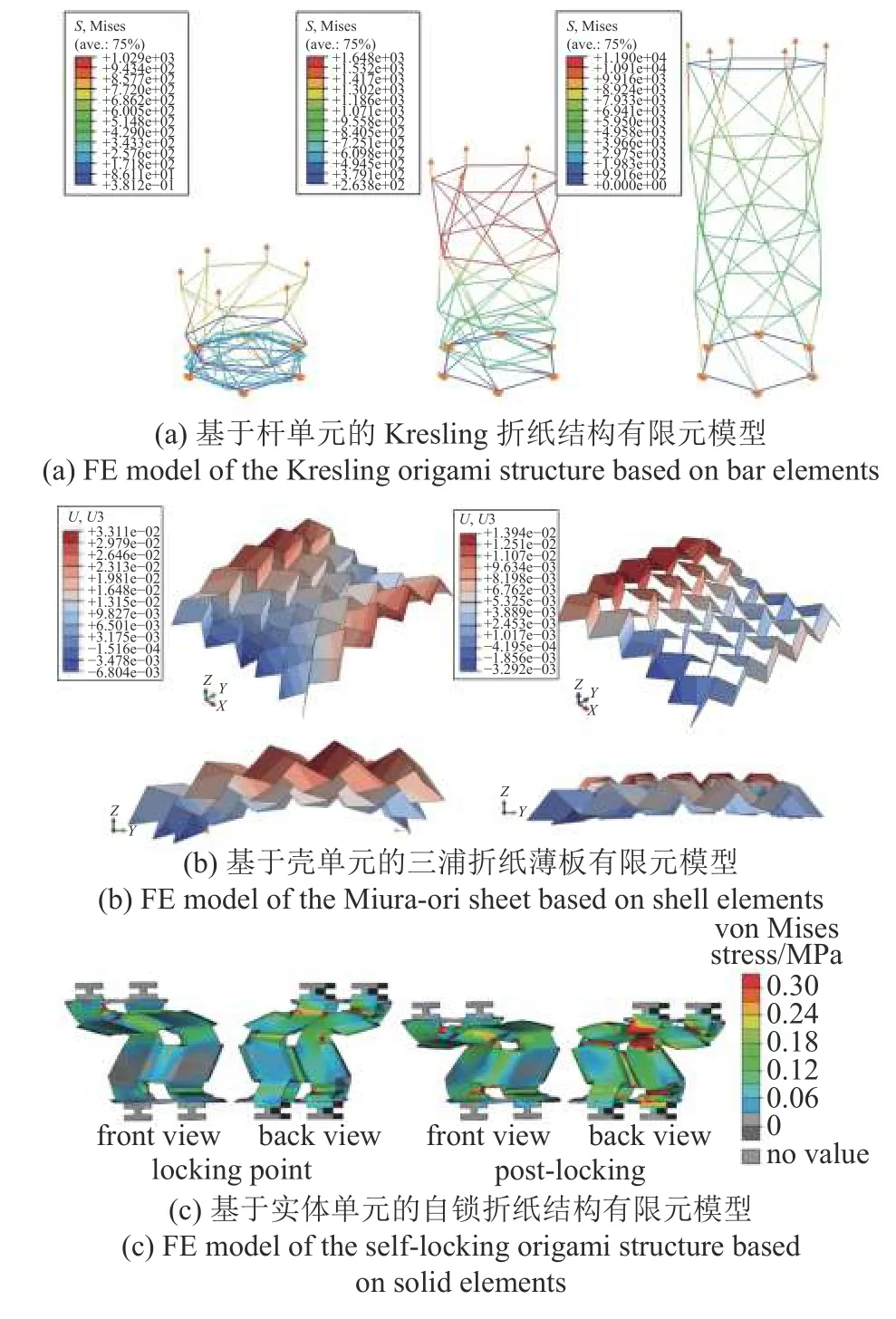
图11 基于不同单元类型的折纸结构有限元模型[30,78,148]Fig.11 FE models of origami structures based on different types of elements[30,78,148]

3.3 动力学实验

折纸结构和折纸超材料动力学实验的主要目的是为了定性或定量地验证动力学模型和数值计算的准确性.具体地,实验研究可以分为以下3 类:(1)施加周期性外部激励以研究折纸结构和折纸超材料的稳态动力学性能;(2)自由和受控展开实验以研究瞬态展开动力学性能;(3)冲击实验以研究抗冲击和能量吸收能力.

对于第1 类实验研究,折纸结构和折纸超材料通常与激振器相连,通过激光位移传感器、加速度传感器、高速相机等获得折纸结构和折纸超材料在周期性外激励作用下的位移(或速度、加速度)-时间历程数据,进而在时域或频域内对信号作分析以获得稳态动力学特性.例如,Fang 等[27]通过激振器对双稳态SMO 结构施加了简谐位移激励(图12(a)),利用激光测振仪获得了其位移-时间历程数据,通过离散扫频并基于FFT 得到了双稳态SMO 结构的频响关系.为了避免重力的影响,SMO 结构整体通过悬吊法固定;为了在同一激励条件下捕获所有可能稳态动力学响应,通过敲击实现初始条件的改变以切换稳态响应.另一个具有代表性的工作来自于Yasuda等[39],他们对Kresling 折纸超材料开展了波动力学测试(图12(b)),利用高速相机记录了Kresling 折纸超材料在周期性位移激励下各单元的位移-时间数据,从而明确了其波传播特性.

对于第2 类实验,通常将折纸结构和折纸超材料的一端固定,通过预压的方式储存势能,另一端自由释放或受控释放,通过高速相机等获取折纸结构和折纸超材料的位移-时间历程数据,从而明确其瞬态展开动力学特性.例如,Wu 等[34]通过类似方法记录了三浦折纸管状结构自由展开时各个标定点的位置,从而明确了其在展开方向和横向方向的瞬态动力学特性(图12(c)).Sadeghi 等[150]将TMP 折纸结构放置在水平面上,将其沿高度方向压缩后自由释放,利用高速相机记录了其在跳跃过程中的运动轨迹,进而分析了其非线性刚度对跳跃性能的影响.

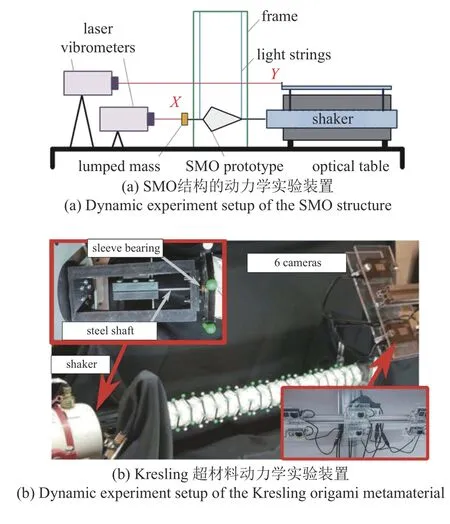
图12 折纸结构和折纸超材料动力学实验[27,34,39,151]Fig.12 Dynamic experiment of origami structures and origami metamaterials[27,34,39,151]

对于第3 类实验,通常是将折纸结构和折纸超材料置于冲击试验机上进行测试,利用试验机自身的力位移传感器或高速摄像机记录冲击发生时的力-位移-时间历程数据和变形情况,进而分析结构的吸能特性.例如,Xiang 等[151]利用分离式霍普金森压杆(SHPB)实验系统测试了SMO 超材料在不同速度冲击载荷下的行为,并通过高速摄像机记录试样变形情况,进而分析结构的吸能特性(图12(d)).Kshad 等[152]利用落锤冲击试验机对由碳纳米纤维增强复合材料制成的三浦折纸结构进行冲击测试,并利用动载荷传感器记录力的数据,以分析三浦折纸结构的能量传递特性.Elsayed 等[153]利用Instron冲击试验机对由牛皮纸制作的多层三浦折纸结构进行了冲击测试,得到了冲击力和能量相对于位移变化的数据,分析了三浦折纸结构在3 个方向的吸能特性.

4 折叠诱发的动力学行为

折叠是折纸结构和折纸超材料的主要变形特征,也是其超常规静力学和运动学特性(1.4 节)的主要来源.在动力学环境下,这些超常规静力学和运动学特性也会诱发独特的动力学行为,包括双稳态和多稳态动力学行为、可编程刚度相关的动力学行为、折叠展开瞬态动力学行为和折纸超材料波动力学行为.下面,从这4 方面进行综述.

4.1 双稳态和多稳态动力学行为

当折纸结构和折纸超材料具有两个及以上的稳定构型(对应于稳定平衡点),且不需要外力就可以维持其稳定构型,则被认为是多稳态的.折纸结构和折纸超材料的多个稳定构型对应于势能超曲面上的多个局部极小值.从动力系统角度来看,多稳态系统的两个稳定平衡点之间必然存在着一个不稳定平衡点.因此,对于多稳态折纸结构和折纸超材料而言,其稳定构型间也必然存在着一个不稳定临界构型(对应于不稳定平衡点).

折纸结构和折纸超材料在不同的稳定构型处常具有不同的动力学特性.例如,waterbomb 折纸结构在不同稳定构型处具有不同的切线刚度,使得不同的小振幅阱内振动呈现出不同的共振频率[74,96],进而改变折纸超材料整体的带隙特征[38]和瞬态展开行为[34].将折纸结构和折纸超材料从一个稳定构型切换至另一个稳定构型时,必然要经过不稳定的临界构型.在通过该不稳定临界构型时,折纸结构和折纸超材料会发生快速的突弹跳跃(snap-through)行为,并在力-位移本构关系上表现为负刚度特征.这种突弹跳跃切换可以通过内部压力[154]或外界简谐激励[27]等方式触发.事实上,负刚度特征在多稳态折纸结构和折纸超材料中广泛存在.通过改变折纸结构内部压力可以将负刚度调整为准零刚度,其在低频隔振上有着很好的效果[18,155].

在外界激励作用下,双稳态这一全局强非线性可以诱发出丰富的动力学行为.例如,对双稳态SMO 结构施加不同频率和幅值的位移激励,可以观察到多种复杂动力学响应,包括围绕不同平衡点的小振幅阱内振动,以及围绕多个平衡点的大振幅阱间振动.FFT 分析表明,这些振动可以与外激励保持相同的频率,也可以是亚谐(sub-harmonic)和超谐(super-harmonic)的,甚至是混沌(chaotic)的[27,96](图13(a)).此外,对应于不同的响应类型,双稳态折纸结构的输入与输出的位移和能量传递率可以表现出很大的差别[27,38,87,103].

多稳态也使得折纸结构和折纸超材料的稳态动力学响应具有显著的初始和外激励条件敏感性.例如,双稳态SMO 结构可以在相同的激励条件下呈现定性不同的稳态响应,且可以通过调整初始条件(例如敲击)实现稳态响应的切换[27].吸引盆为同一激励条件下稳态响应的切换提供了参考依据,而吸引盆稳定性[156]则进一步明确了某一稳态响应的出现概率随结构和激励参数演化的规律[96].此外,通过触发waterbomb 折纸结构在稳定构型处的共振频率,可以用远小于准静态临界力的激励幅值实现不同阱内振动的相互切换[74](图13(b)).

在折叠展开过程中,折纸结构和折纸超材料的最终稳定构型由能障(energy barrier)与其储存能量或外界输入能量的大小关系决定[33,36].通过调整几何设计和刚度布置[27],或通过嵌入磁铁[87]、调整内部压力[154](图13(c))等方式,可以改变折纸结构和折纸超材料的势能本构,进而实现对多稳态特性的定性和定量调控.例如,在磁铁作用下,SMO 结构可以在单稳态和多稳态之间切换,从而定性地改变其频响关系[87].

图13 折纸结构和折纸超材料中的双稳态和多稳态动力学行为[74,96,154]Fig.13 Bistable and multi-stable dynamics of origami structures and origami metamaterials[74,96,154]

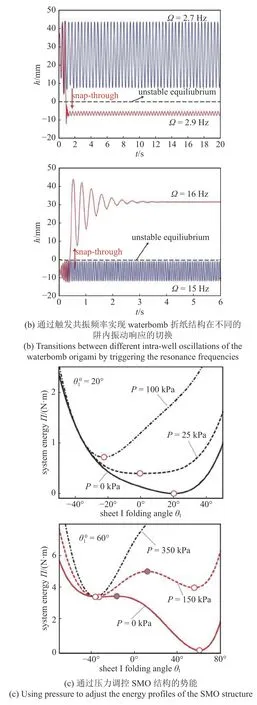
图13 折纸结构和折纸超材料中的双稳态和多稳态动力学行为[74,96,154] (续)Fig.13 Bistable and multi-stable dynamics of origami structures and origami metamaterials[74,96,154] (continued)

4.2 可调刚度相关的动力学行为

如1.4 节所述,折纸结构和折纸超材料具有独特的刚度可调性和可编程性,来源于其折叠行为、自锁和多稳态构型切换、外界部件和作动等.刚度的可调性也使得折纸结构和折纸超材料的动力学行为具备了一定的可调性.这里,由双稳态和多稳态带来的刚度可调性及相关动力学特性的可调性不再赘述(见4.1 节).

自锁也是调节折纸结构和折纸超材料刚度的重要方式之一.Fang 等[30]提出可以通过构成单胞的受控自锁来调节折纸超材料整体的刚度,从而实现幅值显著不同的两类动力学响应;其中一类响应的幅值在非共振的宽频带内明显高于对应的线性系统,而在共振带内则显著低于线性系统(图14(a)).

此外,通过外界部件和外界作动也可以有效地调节折纸结构和折纸超材料的刚度,进而实现动力学特性的可调性.例如,通过调整折纸结构内部压力,可以达到构型切换和刚度控制的目的;内部压力和折痕弹性引起的势能相互作用,还可以使折纸结构呈现出准零刚度,有希望用于隔振器的设计[18,155].研究还发现加压流体折纸结构具有独特的非对称准零刚度特性,显著提高了低频大振幅条件下的振动隔离效果(图14(b)),且可以通过调节内部压力以适应静载荷的变化[18].

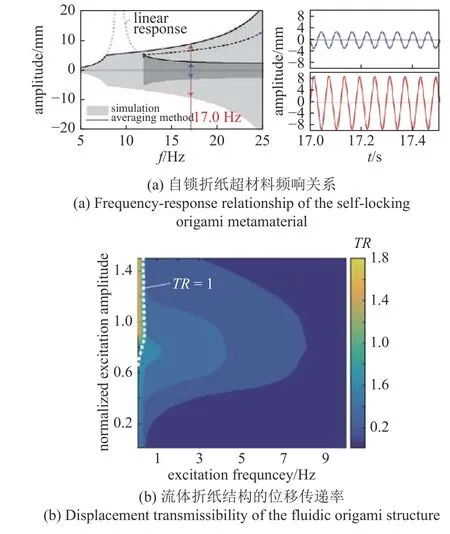
图14 折叠诱发的可编程刚度相关动力学行为[18,30]Fig.14 Programmable stiffness-dependent dynamics induced by folding[18,30]

4.3 瞬态动力学行为

折纸结构和折纸超材料在开发可展开结构、能量吸收装置等方面具有巨大潜力.对于真实的折纸结构和折纸超材料而言,折叠展开本质上是一个动力学过程,且动力学展开过程与运动学展开过程存在显著差异,需要额外关注.例如Zhang 等[101]模拟了可折叠板结构从折叠状态到完全展开状态的整个动态展开过程,发现动力学展开比运动学展开经历了更多的波动.当前折纸结构和折纸超材料瞬态动力学研究的主要关注点有3 个方面:(1)折纸结构和折纸超材料折叠展开过程中沿展开方向与横向方向上的瞬态振动;(2)薄膜类折纸结构展开过程中的应力集中等行为;(3)折纸结构和折纸超材料在冲击载荷下的瞬态动力学行为.

折叠展开过程中,展开方向及横向方向瞬态振动常通过稳定时间和最大振动幅值等关键参数予以表征.Kidambi 和Wang[33,157]基于Kresling 折纸结构的6 自由度等效动力学模型研究发现:通过调整几何设计参数,Kresling 折纸结构可以在单稳态、非对称双稳态和对称双稳态之间切换.对于单稳态结构,可以将其压缩至紧凑状态后释放约束以实现展开;对于双稳态结构,要求初始储存的能量足够大以克服两个稳态间的能障才能实现展开;对于离轴(offaxis) 运动,因其最低固有频率明显高于轴向运动(图15(a)),使得离轴扰动会更快消散.Chen 等[158]提出了基于弹性flasher 折纸结构和剪刀机构的太阳能电池板阵列,并建立了黏弹性本构模型以预测自膨胀展开行为,其包括两个阶段:旋转与环向膨胀.Wu 等[34]分析了预压缩SMO 管状结构自由展开的瞬态动力学行为.动力学实验表明除了在展开方向,SMO 管状结构在横向方向上也存在明显的瞬态振动,其无法通过基于刚性折叠的运动学模型予以描述.研究还进一步明确了几何和物理参数对瞬态振动的超调量和稳定时间的影响.Xia 等[100,159]研究了三浦折纸薄板的自由展开和恒定速度受控展开,在展开过程中,除了沿展开方向的收缩和膨胀,三浦折纸薄板的折面会发生明显的弯曲和拉伸变形,并在横向方向出现明显的瞬态振动.注意到,展开顺序及横向振动的形式与受控展开的速度密切相关.当速度较快时,三浦折纸薄板的受控端单元会首先展开(图15(b));当速度较慢时,三浦折纸薄板中央的单元会首先展开.

薄膜类折纸结构在展开过程中会频繁地遇到折面接触碰撞、应力集中、展开平整度等问题.事实上,薄膜折痕处的力学特性极其复杂.Deboeuf 等[160]指出,薄片的褶皱行为和折叠行为从表面上看具有显著差异,但它们存在一定相似性.Deboeuf 等研究发现,折叠和褶皱产生刚度具有相同的机理,因而折叠的模型可以捕捉褶皱的主要特征;褶皱具有分层特征,类似于多次折叠.Yuan 等[102]考虑了leaf-in 折纸薄膜结构的受控展开问题,分析了膜单元边界和膜单元内部的穿透现象、部分区域的褶皱现象以及完全张紧时的应力集中现象(图15(c)).Cai 等[161]利用有限元软件Abaqus 对三浦折纸膜结构的展开进行了仿真模拟,并基于光滑度指数和完全展开状态下的最大Mises 应力这两个指标评估了加载节点、加载时间和边界形状等因素对展开的影响.研究发现,增加加载节点数目可以有效地降低完全展开状态时的光滑度指数和最大Mises 应力,但多节点加载有可能引起应力集中.Bhuiyan 等[162-163]使用多体动力学(MBD)仿真软件创建了flasher 折纸结构的动力学模型,分析了其展开时间、折纸结构中折痕处的力和力矩、折面弯曲角度和刚性可折性等.研究发现,当引入板内节点时,模型具有刚性可折性,且板内节点在展开过程中可以旋转达到10°～ 35°.

由于具有独特的可控坍塌模式这一优点[164],折纸结构和折纸超材料常用于开发吸能材料和吸能结构,并受到越来越多的关注.例如,Kshad 和Naguib[144]观察到三浦折纸三明治芯(miura-ori sandwich core)结构发生断裂时,折痕会先失效(图15(d)),而折面则呈现刚体旋转运动.利用这种特性,Yuan 等[165]提出可以通过预先设计折痕以调控汽车保险杠在冲击发生时的失效模式.冲击载荷下折纸结构和折纸超材料的瞬态动力学常关注两个指标:能量吸收能力和力峰值.为实现冲击载荷下能量吸收的最大化及力峰值的最小化,许多研究从形状优化[62]、折叠角度设计[166]和材料功能梯度配置[37]等方面开展了数值和实验研究.在折纸箱薄壁管的冲击实验研究中,Zhou 等[167]观察到了3 种坍塌模式,包括完整菱形模式、局部屈曲模式和对称模式.实验结果表明,完全菱形模式的能量吸收效率最高,而对称模式的能量吸收效率最低.

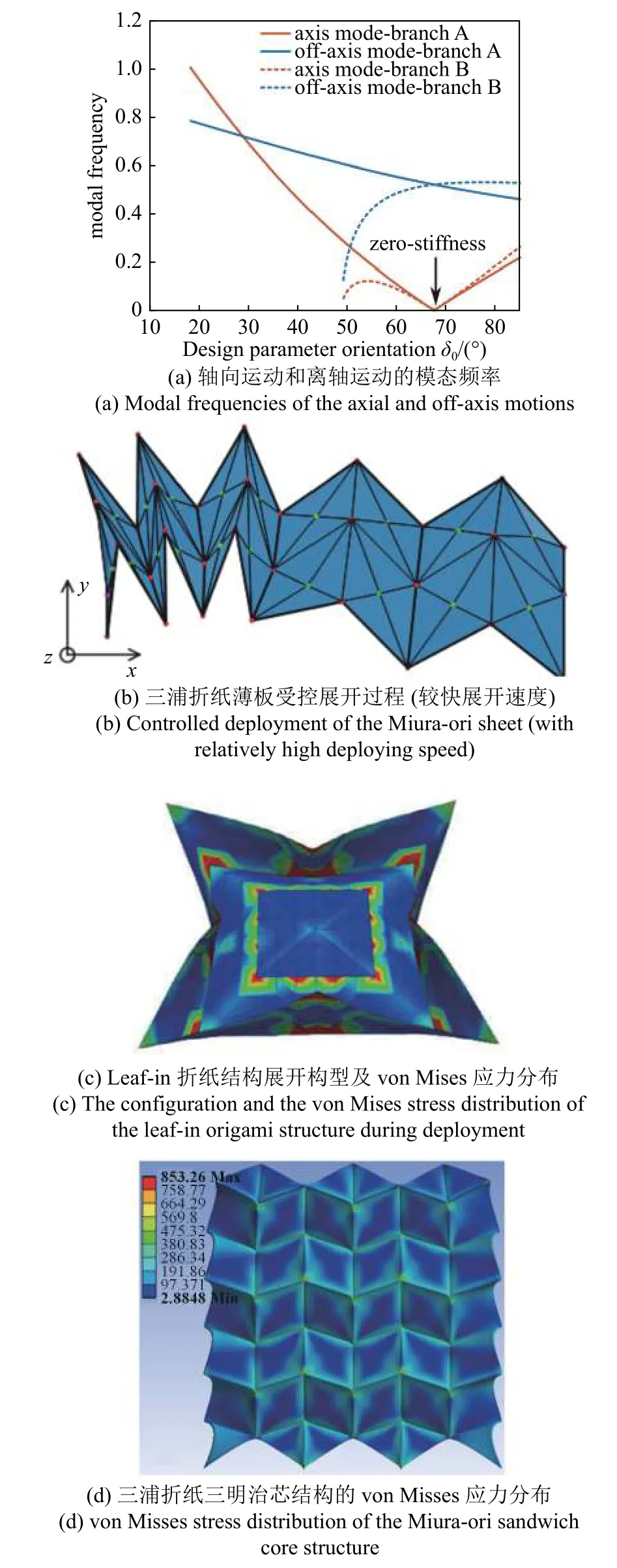
图15 折纸结构和折纸超材料展开瞬态动力学行为[33,102,144,159]Fig.15 Transient dynamic behaviors of origami structures and origami metamaterials during deployment[33,102,144,159]

冲击载荷下折纸结构和折纸超材料瞬态动力学的另一个研究方向是冲击波的传播与衰减.

4.4 折纸超材料波动力学行为

折纸超材料还可以作为波传播的媒介,折纸结构单胞自身的可折叠、多稳态等特性有可能赋予折纸超材料整体出色的波动力学特性.通常,折纸超材料由数目众多的折纸结构单胞构成,人们主要关注波经过折纸超材料后的输出特性(例如,波传播速度、带隙特征、传递率等),而对构成单胞自身的动力学行为并不感兴趣.对于由单个或数目较少的折纸结构单胞构成的系统,可以采用解析或数值方法求解常微分方程,明确每个单胞的动力学行为.而对于由无穷多折纸结构单胞构成的超材料,传统的动力学分析和计算方法面临着自由度高、效率低等局限,而波动力学分析方法,例如线性色散分析、偏微分方程求解等,可以高效地给出折纸超材料中的波传播特性,具有显著优势.

目前,波动力学研究主要关注波在折纸超材料中的传播与衰减(图16(a)).例如,不同幅度冲击力下TMP 折纸超材料中压缩应变波及拉伸应变波的传播速度,以及TMP 折纸超材料中稀疏孤波的存在性和动力稳定性[92],同构及异构TMP 折纸超材料的可调谐波动特性[94].Yasuda 和Yang 等[89]也研究了Kresling 折纸超材料的带隙特征以及压缩冲击波在超材料中的传播(图16(b))[39].实验和数值研究发现,在具有应变软化特征的Kresling 折纸超材料中,压缩冲击产生的压缩应变波会被稀疏孤波所替代,使得后续的Kresling 折纸结构单胞经历拉伸应变,而不是压缩应变,有希望用于开发可重复使用的减震系统.Nanda 和Karami[168]以及Xu 等[169-170]研究了一种简单的一维可折叠超材料,数值计算和实验测试表明,可以通过改变每个折痕的折叠角度来调控超材料整体的带隙分布(图16(c)).Zhang 等[38]研究了由双稳态SMO 单胞构成的超材料的带隙特征.研究发现,通过切换SMO 单胞的构型,超材料整体的带隙会发生定性改变,这赋予了超材料带隙的在线可调性.值得注意的是,上述两类研究中对折纸超材料施加的均为小幅值位移激励,折纸超材料的可折叠大变形特征以及相关的超常规力学特性并没有得到利用.因此,针对SMO 超材料,Zhang 等进一步研究了当位移激励幅值增大时超材料中的波传播(图16(d))[38].数值研究表明,尽管激励频率处于禁带之中,但当激励幅值逐渐增大并超过临界值时,SMO 超材料将出现超传递(supra-transmission)现象.超传递是由SMO 单胞固有的双稳态特性诱发的突弹跳跃所引起的,其可以通过注入能量(injected energy)、发生构型切换的单胞数目、单胞的相对振幅等指标予以体现.当超传递发生时,振动不会在超材料中衰减,而是持续维持.此外,也可以通过切换SMO 单胞的构型实现对超传递发生的临界位移激励幅值进行调控.

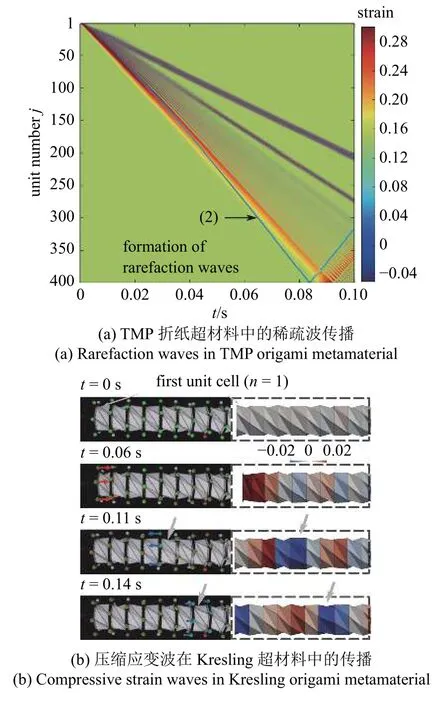
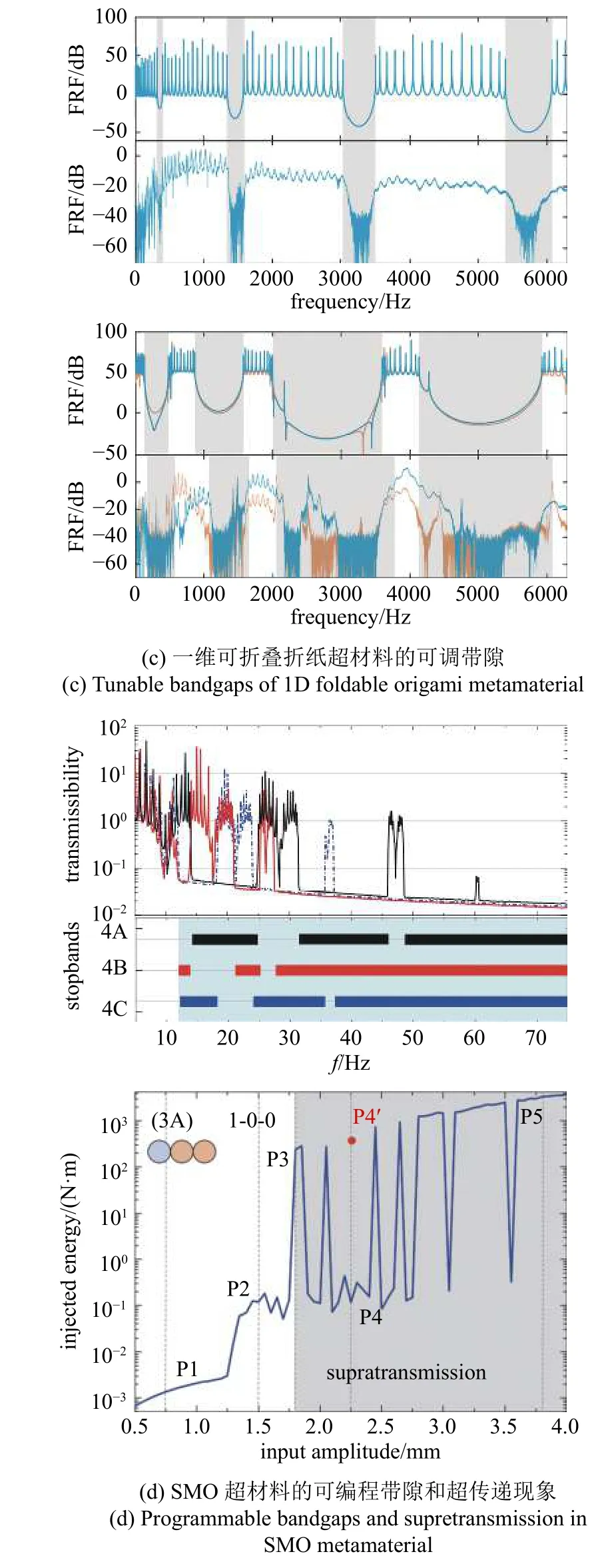
图16 折纸结构和折纸超材料波动力学行为[38-39,92,169]Fig.16 Wave dynamic behavior of origami structures and origami metamaterials[38-39,92,169]

另一类波动力学研究中,波并非在折纸超材料中传播,而是在与其相连接的结构中进行传播.折叠引起的构型改变以及相关的非常规力学特性可以定性和定量地改变与之相连结构的拓扑特性和波动力学特性,进而影响波在其中的传递.例如,在梁和板上布置双稳态Kresling 折纸结构阵列可以形成一维和二维超材料,通过调整Kresling 折纸结构的几何设计或切换其构型,可以有效调控超材料整体的带隙[171].Thota 等[172-173]提出了一种由三浦折纸结构引导的圆管阵列声子系统,三浦折纸结构的折叠变形可以改变圆管阵列的固有对称性特征和晶格类型,从而改变带隙特征并实现可调控波导.

5 折纸结构和折纸超材料动力学应用潜力

折纸结构和折纸超材料具有出色的运动学、静力学和动力学特性,它们在许多工程领域都受到了广泛的关注.目前,折纸结构和折纸超材料的动力学应用主要还停留在实验室原型验证阶段,真正用于实际工程的案例还不多,但正在不断拓展.本节重点介绍折纸结构和折纸超材料在动力学方面的应用潜力.

5.1 折纸启发的隔振和能量吸收装置

折纸结构和折纸超材料常具有折叠大变形和刚度可调等特性,因此在隔振和能量吸收方面展现出了极大的应用前景.折纸结构隔振通常利用了折纸结构的刚度可调特性使得振动在一定范围内被衰减,隔振的效果常通过位移传递率来评估.目前,已有学者提出了基于折纸结构的准零刚度隔振器,其对于低频振动具有较好的隔离效果.例如,Inamoto和Ishida[174]设计了Kresling 折纸结构启发的准零刚度隔振器(图17(a)).该隔振器可以通过调整连杆的角度以及中心轴与弹簧间的间隙实现对静承载能力的调整.动力学实验结果表明,当振动的加速度幅值较大时,该隔振器可以有效隔离2 Hz 以上的振动(传递率小于1.0),而在2 Hz 以下,传递率将大于1.0[175].Han 等[103]提出了SMO 结构启发的非线性准零刚度隔振器,其折叠运动引起的非线性刚度和非线性阻尼可以有效提升低频段下的隔振效果,同时拓宽了有效隔振频带.Yao 等[176]提出了一种受折纸结构启发的用于卫星动力轮组件的多方向隔振器(图17(b)),实验结果表明,外激励频率为20,40 和60 Hz 时,加速度振幅在x方向上分别衰减了96.12%,98.86%,97.06%,在y方向上分别衰减了90.79%,96.1%,99.89%,在z方向上分别衰减了98.96%,99.87%,99.99%,取得了很好的隔振效果.实现准零刚度的另一种方式是通过调控流体折纸内部的压力,Sadeghi和Li[18,155]提出的流体折纸隔振器(图17(c))可以在0～10 Hz 范围内实现有效隔振(位移传递率小于1.0);但是在一些特殊情况下(低激励频率且高激励幅值),位移传递率也可能大于1.此外,通过调节内部压力也使得该隔振器的静承载具备可调性.

图17 折纸启发的隔振和能量吸收装置[18,62,174,176-178]Fig.17 Origami-inspired vibration isolation and energy absorption devices[18,62,174,176-178]

通过利用折叠变形时的能量吸收能力,折纸结构和折纸超材料也被应用于开发能量吸收装置.当前,折纸启发能量吸收装置的动力学研究主要关注冲击载荷下能量吸收能力的增大与反力峰值的降低.Karagiozov 等[37]研究了均匀密度三浦折纸超材料在匀速压缩和脉冲加载下的行为,以及梯度密度三浦折纸超材料在冲击载荷下的行为.研究发现,具有相同拓扑结构但相对密度较高的三浦折纸超材料表现出了更高的比吸能(specific energy absorption,SEA).Ciampaglia 等[62]对具有折纸形状的复合材料盒(图17(d))进行了耐撞性研究.实验表明,经过优化的折纸盒吸收的能量比方形碰撞盒高出15%,比未优化的折纸盒高出30%;在反力峰值方面,折纸盒比方形折纸管有明显降低.Zhou 等[177]研究了梯形折纸结构(图17(e)),发现可以利用折纸图案的塑性变形提升对冲击的吸收能力.Li 和You[178]发现与传统梁结构相比,折纸梁(图17(f)) 的反作用力更恒定,整体能量吸收明显提高(SEA 增加了40%～60%),而负载均匀性(load uniformity,LU)降低了30%～ 40%.

5.2 折纸启发的空间可展开结构

折纸结构因其折叠变形、质量轻的优点,在航天可展结构方面有着广泛的应用前景.当前,折纸启发的空间可展结构研究主要关注概念设计、折叠方式和展开运动学分析等,展开动力学方面的研究还相对较少.

根据航天领域的实际需求,研究者们已经基于折纸思想提出了许多空间可展结构,包括管状的可展开吊杆和薄膜状的可展开太阳反光板、可展开遮星罩等.其中,可展开吊杆主要利用了折纸管状结构出色的轴向折叠和伸缩能力.You 和Cole[82]提出了一种可折叠薄壁圆筒吊杆的概念设计(图18(a)),其可以被折叠成较小体积置入发射仓内.Schenk 等[65]提出一种由铝膜层压材料制成的充气折纸吊杆结构(图18(b)),并研究了不同折纸管状结构的展开特性.而薄膜状的可展开反光板、可展开遮星罩则主要通过结构横向旋转实现展开.Salazar 等[15]提出了两类折痕图(螺旋折痕和同心折痕)来设计可展开太阳反光板(图18(c)).Webb 等[64]提出了一款直径达34 m 的可展开遮星罩概念设计(图18(d)).

图18 折纸启发的空间可展开结构[15,64-65,82]Fig.18 Origami-inspired space deployable structures[15,64-65,82]

航天折纸可展结构的展开本质上是动力学过程,最近也受到了越来越多的关注,研究问题包括应力集中、力和力矩变化、展开时间以及自接触和碰撞等问题.Yuan 等[102]研究了leaf-in 折纸空间薄膜结构在展开过程中出现的应力集中问题和顶点折面之间的接触碰撞问题;Bowen 等[179]使用ADAMS建立了遮星罩的动力学模型并开展了动力学仿真分析;Pehrson 等[69]提出了基于折纸思想的SDSR 空间可展开阵列的设计,并建立了多体动力学模型研究其展开过程.

此外,空间可折叠薄膜结构被广泛应用于航天器再入减速装置、大面积电池阵、大口径星载天线、太阳帆等领域[180-184].注意到,薄膜结构由于材料的柔性特征占主导,其折叠行为与折纸结构具有显著差异,已经超出了本文的范围,在此不做展开.

5.3 折纸启发的波调控装置

折纸结构和折纸超材料在波传播调控方面的具体应用主要可以分为两类:(1) 折纸超材料本身作为波传播的媒介,通过折叠对波传播特性进行调控;(2)折纸超材料本身并不是波传播的媒介,或者波传播与结构本身的折叠变形无关,但是可以通过折叠实现对波传播媒介的调整.对于第1 类应用,其主要利用的是折叠带来的大变形、拓扑变化和非常规力学特性.例如,Yasuda 等[92]设计了拥有应变软化特性的Krseling 折纸超材料,其可以将压缩冲击产生的压缩应变波转换为稀疏孤波,进而实现减震.Xu 等[169]设计了一维可折叠超材料(图19(a)),其可以通过改变折叠结构的折叠角度和折叠处的扭转刚度实现对带隙宽度和个数的调控.

对于第2 类,一般是将折纸结构与波传播媒介相连,通过折纸结构的变形使得波传播媒介发生形状、拓扑、对称性等的改变,从而影响波传播特性.例如Thota 等[173]将一系列圆柱管与三浦折纸结构相连形成声子结构(图19(b)),通过折叠变形改变圆柱管阵列的晶格类型和对称性,进而调控波导特性.Xu 等[185]利用可折叠振子来衰减低频(10 Hz)表面弹性波的传播.此外,也有研究利用折纸结构的构型可变特性来调控声波的传播.例如,Babaee 等[20]设计了基于extruded cube 折纸结构的超材料,通过改变超材料折叠角度,可以对声能的传播和辐射进行调控(图19(c)).

图19 折纸启发的波调控装置[20,169,173]Fig.19 Origami-inspired wave tailoring devices[20,169,173]

5.4 折纸机器人

折纸结构丰富的折痕设计和出色的变构型能力,也受到了机器人领域学者的广泛关注[5].目前,已有研究通过主动智能材料实现了折纸机器人从二维薄板到三维构型的自折叠成型和主动作动.主动驱动主要可以分为两类:(1) 将折纸机器人的折痕设计为主动折痕,在外界物理场(例如热场、磁场等)的作用下实现主动折叠、主动成型和主动构型重构;(2) 在折纸结构内部或外部布置驱动器(例如舵机、气囊等),对机器人进行整体驱动.代表性研究包括:Felton 等[6]在折纸机器人的折痕处布置了由形状记忆材料制作的夹层结构,通过电流加热使机器人由二维平面自折叠成为三维结构(图20(a));Paez 等[186]研发了基于Yoshimura 折纸结构的驱动器(图20(b)),通过其内部气囊的充气和放气实现整体的作动;Zhang 等[187]还提出了基于Yoshimura 折纸结构、形状记忆合金弹簧和内部气囊的具有三维移动能力的仿蠕虫机器人(图20(c)).

目前,大部分折纸机器人研究停留在准静态阶段,只利用了折纸结构的丰富变形模式.例如,Liu等[188]使用Twisted Tower 折纸结构设计了机械臂,利用该结构独特的拉、压、弯、扭4 种变形模式实现了出色的空间可达性.Sareh 等[189]则以三浦折纸结构为基础设计了无人机的防碰撞装置(图20(d)),利用三浦折纸结构的变形能力提升了无人机的抗冲击能力.

图20 折纸机器人设计和实验原型[6,186-187,189-191]Fig.20 Designs and prototypes of origami robots[6,186-187,189-191]

随着对折纸结构研究的不断深入,学者们发现,折纸结构所特有的非常规力学特性对机器人性能提升也具有重要意义.例如,Fang 等[17]利用waterbomb折纸结构的双稳态特性,设计了可在管道中运动的仿蠕虫移动机器人.Lee 等[190]则是利用了waterbomb折纸结构的双稳态特性设计了可变直径轮子的机器人(图20(e)),以实现在狭窄环境中的移动.此外,Kim 等[16]设计了一种可以自锁的折纸结构,并据此设计了一款可以完全折叠的机械臂,自锁的特性使得机械臂在完全伸长时拥有更大的刚度从而提高稳定性.

上述折纸机器人用到了折叠诱发的静力学特性,而将折叠动力学特性用于机器人设计的研究目前还较少.Sadeghi 等[150]设计了一种基于TMP 折纸结构的跳跃装置,并基于动力学特性分析对其几何设计进行了优化.Bhovad 等[191]利用Kresling 折纸结构设计了仿蠕虫移动机器人(图20(f)),并利用Kresling 折纸结构的snap-through 行为实现了机器人步态的切换.此外,Zhakypov 等[192-193]设计了一种可折叠的Tribot 机器人,该机器人可以实现爬行和跳跃步态;动力学建模和分析为机器人的优化设计和控制提供了依据.

6 若干值得关注的问题

上述综述表明,折纸结构和折纸超材料的动力学研究正处于快速发展阶段,还有许多问题需要进一步研究.以下,列举出值得关注的若干问题.

(1) 针对刚性可折条件无法严格满足、折面和折痕厚度无法忽略的折纸结构和折纸超材料,提出精细化动力学建模方法,探索第一性原理和数据驱动方法融合的动力学建模方法.建立的动力学模型不仅需要包含折痕和折面的几何特征、惯性、弹性和阻尼等因素,还需要具备处理折面、折痕间的接触、碰撞和摩擦等问题的能力,同时保持较高的计算效率,服务于动力学设计和优化.

(2) 针对含有缺陷的折纸结构和折纸超材料,研究其动力学建模与设计优化问题.缺陷可以是客观存在的,如材料缺陷和工作时的破坏等;缺陷也可以是人为引入的,例如在超材料设计中引入异构单元,以调控超材料整体的折叠行为,实现对某项动力学特性的优化.

(3) 针对由折叠诱发的全局强非线性本构(例如多稳态等),研究折纸结构和折纸超材料复杂动力学行为的发生机制和演化规律.全局强非线性动力学行为的定性和定量分析方法一直是动力学研究的难题.考虑到折纸结构可以成为实现各类非线性特征的理想平台,以折纸结构为对象推进非线性动力学研究,可以为该学科带来新的活力.

(4) 针对展开、构型切换、跌落和冲击等工况,研究折纸结构和折纸超材料的瞬态动力学和随机动力学行为.例如,折纸机器人在运动到指定构型后,常会发生非期望瞬态振动,因此需要分析该振动产生的原因,通过优化几何设计和驱控方式,实现对该非期望瞬态振动的抑制.

(5) 针对波传播问题,研究将折纸超材料作为波传播媒介时的波动力学特征,重点关注折叠大变形及相关静力学和运动学特性对波传播和能量传播的影响.探索通过折纸超材料实现波的可控折射、反射、透射、拓扑保护和非互易性等超常规特性.

(6) 针对长时间工作情况,研究折纸结构和折纸超材料的动疲劳问题.例如,在周期性外激励作用下,某些折痕会经历长时间的快速和大幅度折叠变形,这就需要考查折痕的动态疲劳强度,研究疲劳破坏的发生和传播.

(7) 针对工程中对可调性的需求,研究折纸结构和折纸超材料动力学特性与波传播特性的主动调控.例如,可以将主动智能材料与多稳态折纸结构有机结合,通过主动构型重构,实现对折纸结构稳态动力学行为和波动力学行为的定性调整;进一步地,可以基于“可再编程(re-programmable)”思想,实现动力学响应和波传播的“数字化”调控.

(8) 针对折纸结构和折纸超材料所特有的复杂三维构型和折叠大变形特征,完善其动力学实验方法.需要重点关注实验原型的加工制备方式和载荷的施加方式,边界的固定方式,全局刚体位移和局部材料变形的同步观测方法等.

(9) 针对工程中的极端因素,研究折纸结构和折纸超材料的极端力学行为及其机制.常见的极端因素包括尺寸极端性、材料极端性和极端物理场作用等.在这些因素作用下,折纸结构和折纸超材料的静/动力学行为将发生显著改变,甚至诱发一系列超常规力学行为和超常规力学特性,这就需要重新思考“折纸”力学研究的基本理论和基本方法,从建模、分析、计算和实验等多方面深入研究“折叠行为”和“极端因素”耦合下的变形、强度、破坏、稳态频响和瞬态响应特性.

(10) 针对实际工程应用需求,提出基于折纸思想的工程结构、机构和装置设计(例如:准零刚度隔振器、快速作动器、冲击防护栏等),以突破现有技术局限,提升相关动力学性能.

7 结语

近年来,折纸结构和折纸超材料引起了学术界和工程界的广泛关注,其理论和应用研究取得了长足发展.开展折纸结构和折纸超材料动力学研究具有必要性、交叉性和重要性.首先,折纸结构和折纸超材料将不可避免地在动力学环境下工作,且它们的折叠、展开和构型切换本质上都属于动力学过程,因此,开展相应的动力学建模、动力学行为预测、动力学机制分析、动力学性能优化和调控等研究,是折纸结构和折纸超材料应用于工程实际的必由之路.其次,折纸结构和折纸超材料具有复杂的几何非线性、突出的大变形和刚柔耦合等特征,以折纸结构和折纸超材料为对象开展动力学研究,建立起几何学、静力学、运动学与动力学的联系,并与材料、机器人及生物医学等应用领域进行关联,将极大地丰富传统动力学的研究范畴和学科内涵,突显了折纸结构和折纸超材料动力学研究的多学科交叉属性.再次,“折纸”思想为工程材料、结构和器械的设计提供了无限的灵感,通过明确折纸结构和折纸超材料在不同工况下的动力学行为,发掘由折叠诱发的超常规动力学特性,有助于解决一些传统材料和结构无能为力的问题,使得折纸结构和折纸超材料与多个领域的工程实际结合更加紧密.

本文对折纸结构和折纸超材料的动力学研究进行综述.为保证完整性和提高可读性,首先概述了“折纸”研究的基本定义和假设,归纳了常见折纸结构和折纸超材料的几何设计与静力学特性.随后,从动力学建模方法、动力学分析和实验测试、折叠诱发的动力学行为以及动力学应用4 个方面介绍了相关研究进展.在动力学建模方法方面,分别介绍了空间桁架等效建模方法和非线性弹簧等效建模方法、基于广义哈密顿原理的建模方法和数据驱动建模方法,还讨论了与建模密切相关的约束和接触的处理方式以及参数辨识问题;在动力学分析手段方面,分别介绍了基于模型和有限元的分析方法以及动力学实验测试方法;在动力学特性方面,分别介绍了与多稳态、可调刚度相关的动力学行为,以及瞬态动力学和波动力学行为;在动力学应用方面,分别介绍了折纸启发的隔振装置、波调控装置、空间可展开结构和折纸机器人等.尽管本文已有非常宽的覆盖面,但限于作者有限的学识,仍存在挂一漏万的可能性.

本文最后指出了折纸结构和折纸超材料动力学领域若干值得关注的问题.在未来研究中,折纸结构和折纸超材料可以作为动力学理论研究与应用开发相结合的新平台,一方面为动力学这一传统学科带来新的研究对象,另一方面也为工程应用提供全新的思路.