考虑振动非平衡的可压缩库埃特流动及其传热1)

罗 健 王智慧

(中国科学院大学工程科学学院,北京 100049)

引言

高温非平衡流动条件下的气动力/热精细预测是新型近空间高超声速飞行器研制过程中面临的关键难题之一[1-4].在新的流动物理下,经典预测理论失效,传统实验和计算手段也难以满足当前工程需求.为了解决此问题,一方面需要发展新的实验技术和计算手段[5-14],另一方面也亟需分析具体流动特征和讨论主要物理机制,探索和建立新的模型理论.对非平衡流动和传热机理的深入认识,也有助于发展相应的实验和计算方法.

一般来说,非平衡流动模型理论的建立,需要针对主要的高温真实气体效应,并结合具体的流场结构特征.根据飞行高度和速度的差异,不同飞行器所遭遇的高温真实气体效应也不同[15].当飞行器再入或高速滑翔飞行时,化学非平衡效应占主导作用;当飞行器巡航速度相对较低(马赫数Ma=5～10)时,振动非平衡效应更加重要,而气体离解等化学反应过程的影响可以忽略[16].对振动非平衡的研究,一方面聚焦于微观层面的振动激发速率的研究[17-21],另一方面聚焦于振动激发对于飞行器气动力/热的影响[22-24],例如,Schubert[24]研究发现在特定条件下振动非平衡会使得总热流变化14%左右.为了更加精细地模拟振动非平衡过程,在计算流体动力学(computational fluid dynamics,CFD)、直接模拟蒙特卡罗(direct simulation of Monte Carlo,DSMC)[25]等计算方法中都先后引入了精细的振动激发模型[26-30].最近,Luo 和Wang[31]提出了振动非平衡和化学非平衡流动之间的比拟关系,并从理论上讨论了振动非平衡及壁面振动能非完全适应对驻点热流预测的影响,但尚未讨论驻点下游流场中的非平衡特征.

根据流场结构特征的差异,飞行器不同部位的流动可大致分为3 类:机身体前缘和翼缘驻点附近的强压缩流动、机身和机翼表面的强剪切流动以及凸起物和缝隙等结构处的复杂干扰流动.不同类型流动的动量、能量输运机理存在显著的差异,需要有针对性地建立其流动模型,发展相应的气动力/热预测理论.如图1 所示,驻点附近的强压缩流动常用圆柱或圆球绕流模型来模拟,而驻点下游的强剪切流动则为边界层流动模型.驻点气动加热是气动热防护设计的重点关注对象,驻点下游流动和传热特征则显著影响飞行器摩阻和加热总量的预测.由于问题复杂性,高温非平衡边界层传热的一般性理论目前尚未建立起来.事实上,即使对于另一个相对简单的剪切流动模型-库埃特(Couette)流动,高温非平衡效应下的传热特征也缺乏理论描述.对非平衡库埃特流动的研究,可以揭示强剪切非平衡流动物理和传热特征,对最终建立非平衡边界层流动理论也具有重要的参考意义.另外,根据流动主控因素的相似性,简单流动模型中所得到的非平衡流动判据等,也可以推广到更复杂的流动模型,并定性或半定量地解释工程实际中遇到的非平衡气动加热现象.例如,通过调整库埃特流动的速度和温度边界条件,可近似模拟驻点下游不同站位或不同条件下的边界层型流动特征[32].

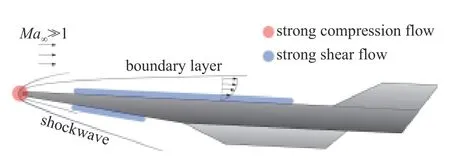
图1 高超声速飞行器周围流场结构示意图Fig.1 Schematic of the flow over a hypersonic vehicle

前人从各个角度对库埃特流动进行了广泛而深入地研究.Illingworth[33]最早在1950 年给出了量热完全气体可压缩库埃特流动的理论解.Liepmann等[34-35]推导了化学离解平衡条件下库埃特流动的绝热壁焓和恢复因子.库埃特流动作为最基本的剪切流动模型也被用来研究稀薄气体效应和气固相互作用等对动量/能量输运的影响[36-38].最近,Abramov 和Butkovskii[39]仍然基于库埃特流动模型,讨论了不同稀薄程度下的雷诺比拟关系;Chen 和Zhou[5]基于库埃特流动模型分析了高超声速稀薄流动中的等效输运系数.可压缩库埃特流动模型在保留典型强剪切特征的前提下,能够极大地降低真实流动的复杂性,有利于明晰非平衡流动物理以及气固相互作用的影响[40].

对于高超声速强剪切流动的气动力/热预测,参考温度(焓)方法和雷诺比拟关系发挥着重要作用.通过计算参考温度下的气体热物性参数,可以推广不可压缩边界层理论公式来近似预测可压缩边界层的壁面摩阻.雷诺比拟关系给出了强剪切流动摩阻和热流之间的关联,结合参考温度方法得到的摩阻即可求得可压缩强剪切流动的壁面热流.参考温度方法这一概念最早由Rubesin 和Johnson[41]提出,用以估计可压缩边界层内流体的平均属性.Dorrance[42]和Eckert[43]分别给出了层流边界层中参考温度的理论计算公式.Young 和Janssen[44]提出了高马赫数下的参考温度计算式.雷诺比拟关系的发展与参考温度方法在同一时期,Reynolds[45]最早提出了摩阻和热流二者之间存在比拟关系的假设.Van Driest[46]在1952 年证明了比拟关系在层流边界层中确实是近似成立的;当高温真实气体效应显著时,Cohen[47]给出离解平衡气体模型参考温度的关联式,并据此修正了离解平衡气体模型的雷诺比拟关系;Debrestian 和Anderson[48]以及Ott 和Anderson[49]发现,对于化学非平衡气体,可以根据数值模拟结果引入关联因子,通过参考温度方法和雷诺比拟关系仍然能够近似预测壁面摩阻和热流.综合来看,前人对于参考温度和雷诺比拟关系的研究大多是基于数值计算或实验结果,给出后验性的关联式.对于高温真实气体效应的讨论也多局限于参数的拟合与修正,缺乏对物理机理的深入讨论.特别是,对于目前关注的振动非平衡的强剪切流动,仍然缺少参考温度和雷诺比拟关系的相关理论研究.

本文将基于库埃特流动模型,研究高超声速剪切流动中动量和能量的输运规律.首先,在量热完全气体模型下推导得到了可压缩库埃特流动的参考温度,揭示了可压缩性对强剪切流动摩阻和热流的影响机理.然后讨论了振动非平衡效应对于参考温度和雷诺比拟关系的影响,进而给出了振动非平衡气体库埃特流动的摩阻和热流预测理论.最后,采用DSMC 数值方法[25],对模型理论进行了验证,并讨论了非平衡传热特征.

1 研究思路与方法

1.1 流动模型

平面库埃特流动是经典的剪切流动模型,如图2所示.由两个做相对平行运动的无限大平板驱动,在剪切应力作用下,足够长时间后形成的一维定常流动,流动参数只沿壁面法向(y方向)变化.设两平板之间的间距为H,下平板为固定壁面,速度为 0,温度为Tw;上平板切向速度为U∞,温度为T∞,约定上平板的温度高于下平板,即T∞＞Tw.根据高超声速飞行器的实际飞行状态,库埃特流动边界条件的取值限定在一定范围之内,上边界速度U∞= 2～6 km/s,温度T∞=1000 K～4000 K,下边界温度Tw=300 K～2000 K .由于振动非平衡流动过程满足二体碰撞相似律[15],数值模拟与真实流动的稀薄程度保持一致,Knudsen 数Kn=10-4～10-2,表明整体流动处于近连续区.

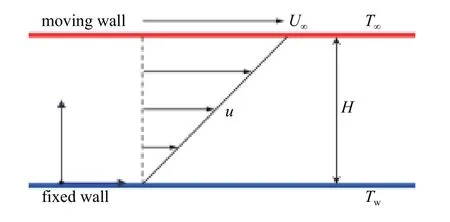
图2 库埃特流动示意图Fig.2 Schematic of the Couette flow

1.2 物理分析

库埃特流动中的能量传递与转化的过程可以用模型示意图3 说明.对于量热完全气体,库埃特流动的传热过程可以分为两部分,一部分是由上下边界温度差或内能差(etr,∞-etr,w)驱动的导热过程,能量以气体分子平转动能etr的形式由上边界传递到下边界;另一部分是剪切黏性耗散产生的热量evis,这部分能量会同时向上下边界传递.同时,黏性耗散产生的热量引起流场中温度升高,气体热物性参数也会发生相应变化.

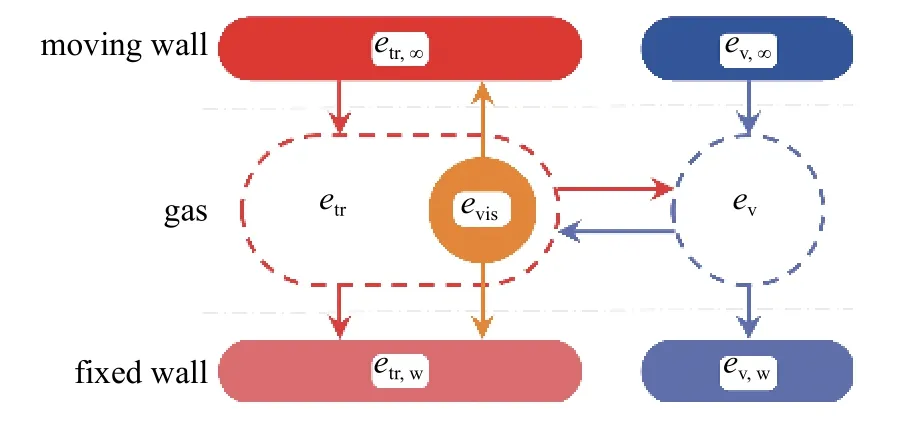
图3 热完全气体库埃特流动中能量传递与转化的广义模型Fig.3 General model of the energy transfer and conversion in the Couette flow of a thermally perfect gas

图4 中蓝色实线展示了可压缩库埃特流动的速度u、温度T、黏性系数 μ 的分布剖面.由于黏性系数随温度发生变化,速度已经不再是线性分布.参考温度方法将可压缩流动与某一虚拟的等温不可压缩流动等效,该不可压缩库埃特流动各物理量的分布剖面如图4 中蓝色虚线所示.其虚拟温度场是均匀的,由于库埃特流动中压强不变,因此虚拟密度场也是均匀的.流动可压缩性的影响被等效地归结到参考温度的变化上,参考温度相较T∞变化得越多,说明可压缩性对流动的影响越大.

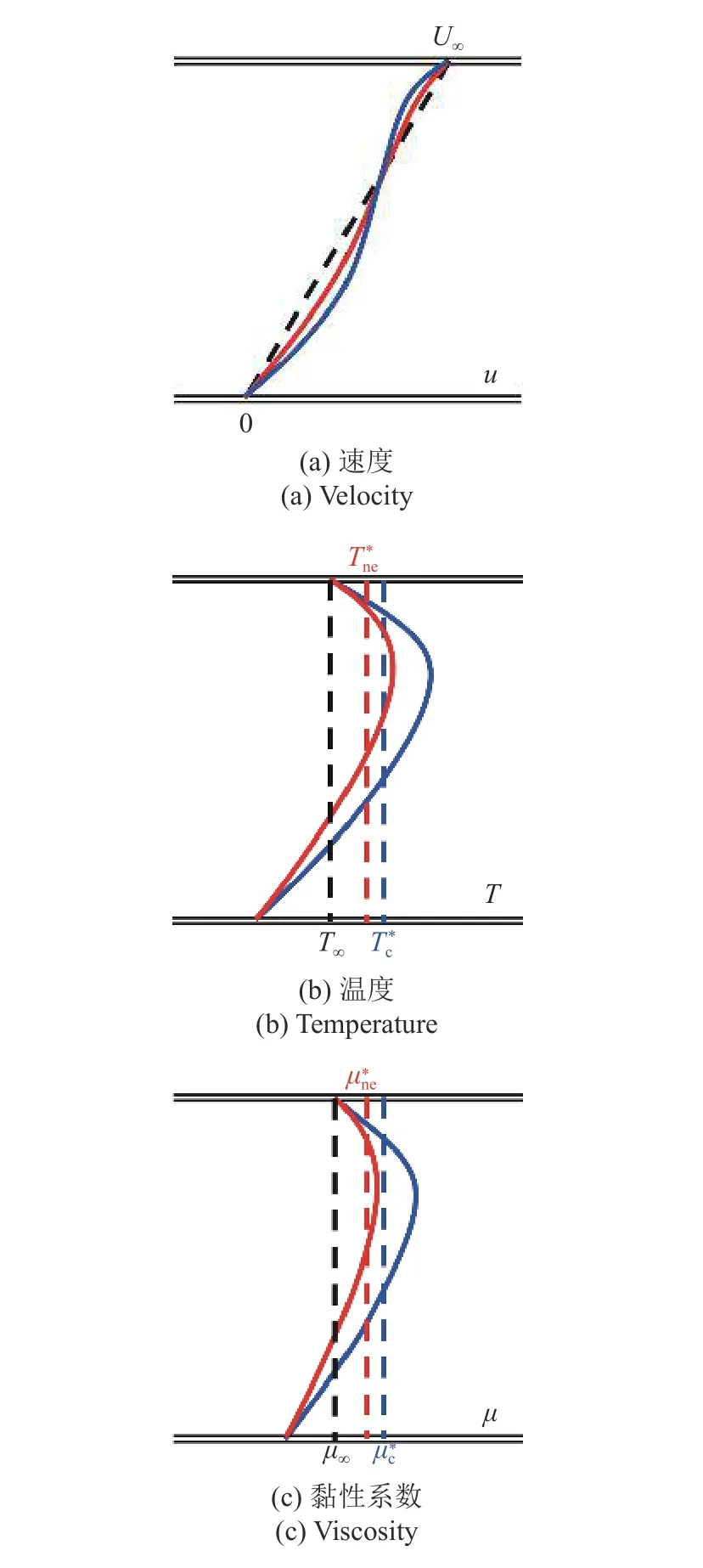
图4 高超声速库埃特流动剖面示意图Fig.4 Profiles of the hypersonic Couette flow

进一步,当流场中温度升高后,高温真实气体效应逐渐显著.本文只关注振动非平衡效应对流动和传热的影响,不考虑化学反应过程,并假设气体分子的平动与转动模态一直处于平衡状态.当气体分子的振动模态激发后,振动能也将参与到传热过程中,如图3 右半部分所示.一方面,上下边界的振动能之差(ev,∞-ev,w)驱动振动能导热过程;另一方面,流场中平转动能etr与振动能ev之间还存在着能量交换,即振动弛豫过程.一般来说,振动能导热过程与振动弛豫过程速率的差异将导致流动处于振动非平衡状态.由于气体分子振动模态的激发,平转动温度剖面小幅度降低(如图4(b)中红色实线所示),此时等效不可压缩流动的参考温度需要进行二次修正,修正后的参考温度与振动非平衡程度相关,振动冻结极限下修正量为0,平衡极限下修正量则最大.

在高超声速库埃特流动中,流动可压缩效应对参考温度的影响是主要的,振动非平衡效应在此基础上叠加了小幅度修正.采用修正后的参考温度,就可以根据不可压缩流动理论得到实际可压缩流动情况下的壁面摩阻.若要得到壁面热流,除了讨论摩阻的修正,还需要确认雷诺比拟关系是否受振动非平衡效应影响.通过提炼关键物理过程的无量纲判据,最终可建立完备的振动非平衡库埃特流动动量、能量输运的理论体系,为进一步研究更复杂强剪切流动模型的气动力/热规律奠定基础.

1.3 计算方法

DSMC 方法是一种基于微观分子运动论的唯象物理模拟方法,是目前稀薄流动领域应用最广泛、公认可靠的数值研究手段.本文将采用Bird 开发的开源DSMC 程序DS2 V[25]对提出的预测理论进行验证和标定.在计算中,选取氮气 N2流动作为研究对象,分子碰撞模型采用了变径硬球模型,黏性-温度指数律的幂指数 ω=0.74 .内能弛豫模型采用广义的Larsen-Borgnakke 模型,其中转动能是连续的,转动弛豫数为5;振动能描述采用间断的量子态能级模型,振动弛豫数根据碰撞对的相对碰撞能和振动能来计算.二维计算域的左右为周期性边界条件,上下边界设为壁面,气体分子与壁面之间为完全漫反射,且能量完全适应.计算网格为矩形网格,计算过程中程序自动根据当地的稀薄程度进行加密,计算时间步长小于分子平均碰撞时间的三分之一,每个网格内的分子数为 10～20 个,满足了DSMC 数值模拟的标准.

2 理论分析与验证

2.1 量热完全气体的可压缩修正

对于量热完全气体,库埃特流动的动量能量守恒方程及其边界条件为

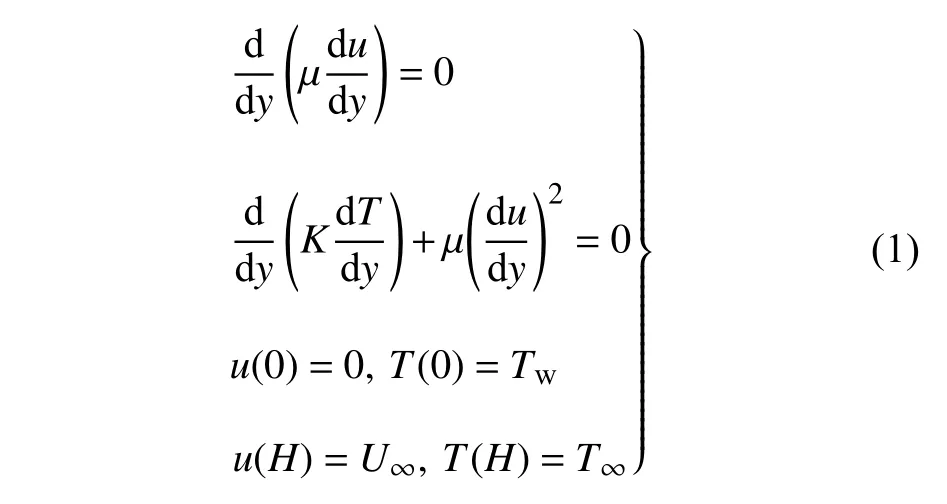
其中 μ和K分别表示气体的黏性系数和导热系数.引入无量纲变换

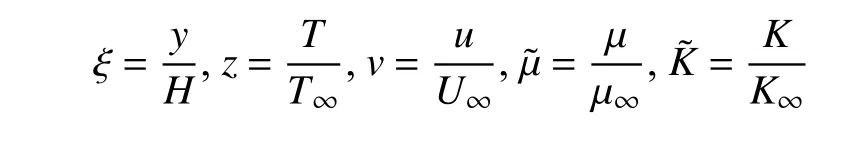
方程可以改写为无量纲的形式

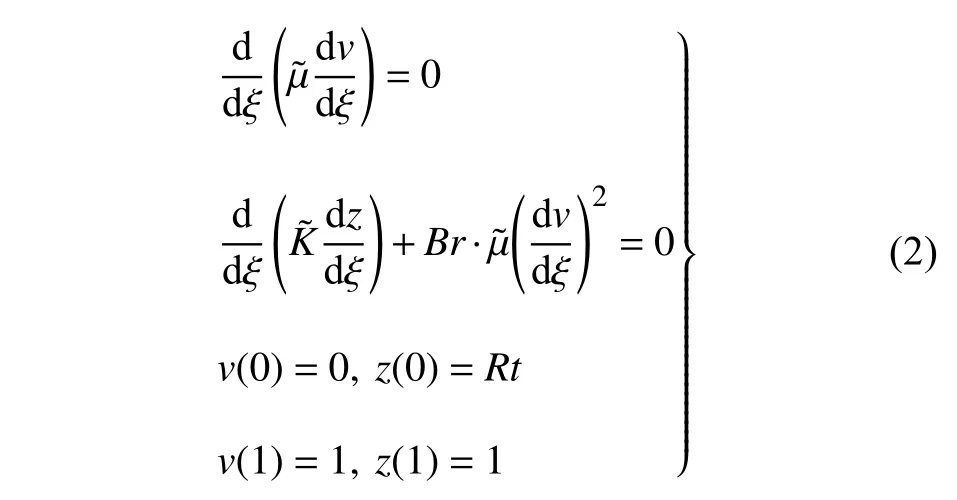
其中无量纲的Brinkman 数Br=Pr·Ec,Prandtl 数Pr=cpμ∞/K∞表征气体动量和能量输运能力的相对强弱,Eckert 数表征剪切耗散效应的相对大小,cp是气体的定压比热容.边界条件无量纲化得到的参数Rt=Tw/T∞表征了纯导热过程的强度.通过无量纲分析可知,量热完全气体的可压缩库埃特流动完全由特征参数Br和Rt控制.

黏性系数 μ 和导热系数K随温度的变化可以采用幂律表示为

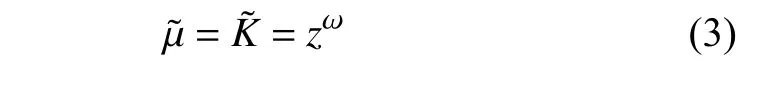
由于幂次形式的特殊性,可压缩库埃特流动速度、温度剖面的理论解难以得到显式表达式,但可以通过数值计算得到其精确解,如图5 中黑色实线所示.图中符号点代表DSMC 的计算结果,两个算例的边界条件(U∞,Tw,T∞)不同,但无量纲参数Br和Rt相同.

从图5 可以看出,相同的无量纲参数的算例有相同的归一化速度、温度剖面,说明对于量热完全气体的可压缩库埃特流动,其控制参数确实是Br和Rt.另一方面,DSMC 模拟的结果和精确解吻合得很好,说明DSMC 作为数值计算工具在当前问题中具有足够的精度,可以用于进一步的讨论分析.

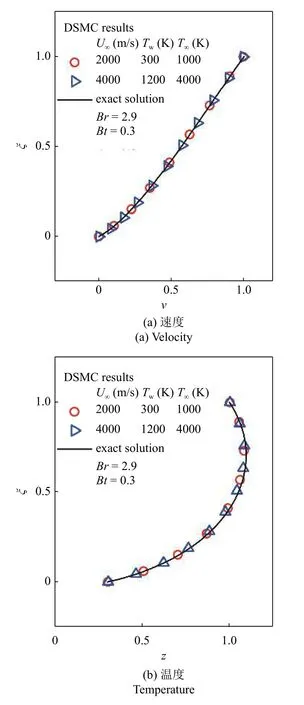
图5 量热完全气体库埃特流动剖面Fig.5 Profiles of the Couette flow of a calorically perfect gas

下壁面的摩阻系数Cf为

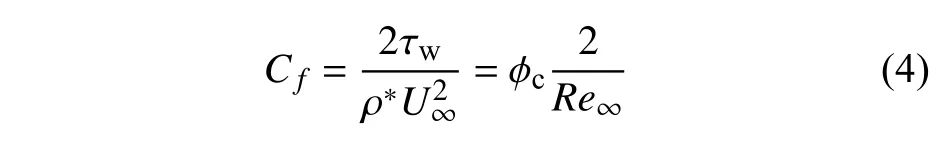
其中,τw是下壁面切应力,ρ*是可压缩库埃特流动的平均密度,雷诺数.φc表征了可压缩条件下壁面摩阻系数相较于不可压缩流动情况Cf,inc=2/Re∞的修正,不妨将其定义为可压缩修正因子.根据前人对可压缩库埃特流动的研究[35],当黏性系数和导热系数与温度之间满足幂次关系(3)时,可压缩修正因子 φc可以表示为特征参数Br和Rt的积分形式

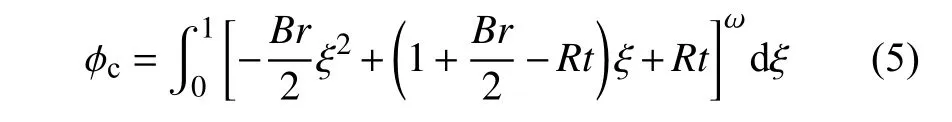
可压缩库埃特流动的壁面热流可以根据摩阻系数以及雷诺比拟关系得到.对于量热完全气体模型,库埃特流动中速度与温度满足能量积分关系[35]

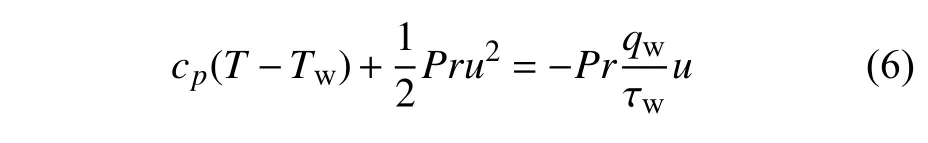
其中qw为下壁面的热流.引入Stanton 数

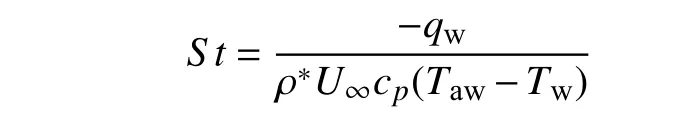
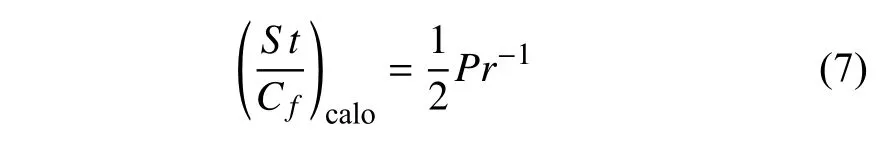
因此,可压缩库埃特流动的Stanton 数可以表示为

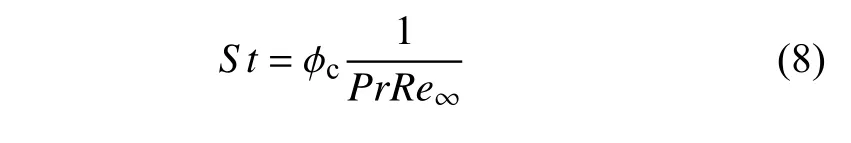
式(4)和式(8)分别给出了量热完全气体模型下可压缩库埃特流动的摩阻与热流,然而可压缩修正因子 φc的积分形式(5)求解不便.工程上经常采用参考温度方法来估计边界层流动的可压缩效应,本文借鉴这一思想来考虑可压缩性对库埃特流动与传热的影响.为了尽可能准确地估计流动可压缩性对热物性参数的影响,需要参考温度能够反应流场的全局温度,前人利用温度剖面的积分平均值来近似估计[42]

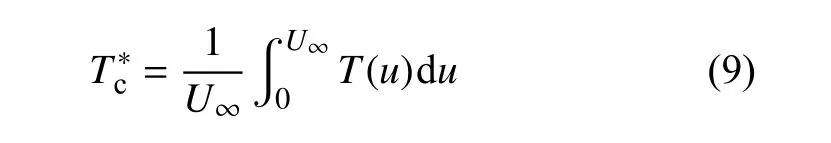
代入温度T与速度u的能量积分关系式(6),积分后得到可压缩库埃特流动的参考温度

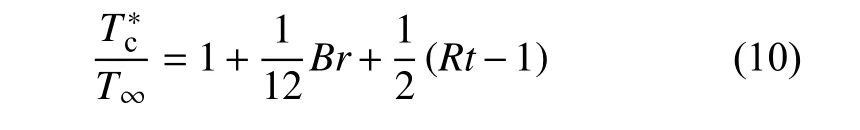
可压缩修正因子φc可以用参考温度表示

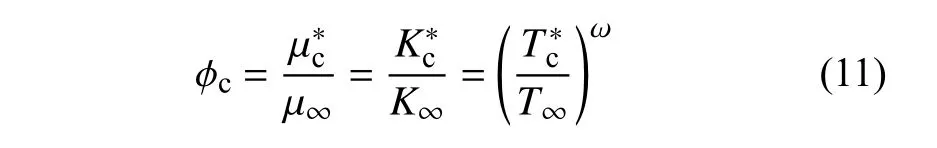
图6 显示了可压缩修正因子 φc随控制参数Br和Rt变化的等值线图.当Br＞6(1-Rt) 时,可压缩修正因子 φc＞1,剪切耗散作用占优,摩阻因流动的可压缩性变大;当Br＜6(1-Rt) 时,可压缩修正因子φc＜1,上下边界温差造成的热传导作用占优,摩阻因流动的可压缩性变小.当Br≈6(1-Rt) 时,可压缩修正因子 φc≈1,此时剪切耗散作用和边界导热作用相互抵消,可压缩性对热物性参数的修正量为 0 .通过参考温度方法得到的近似修正理论与此规律一致,图6 中虚线为近似修正理论(11)给出的修正分界线Br=6(1-Rt) ,与精确解的等值线 φc=1 几乎重合,说明了参考温度公式(10)的合理性.

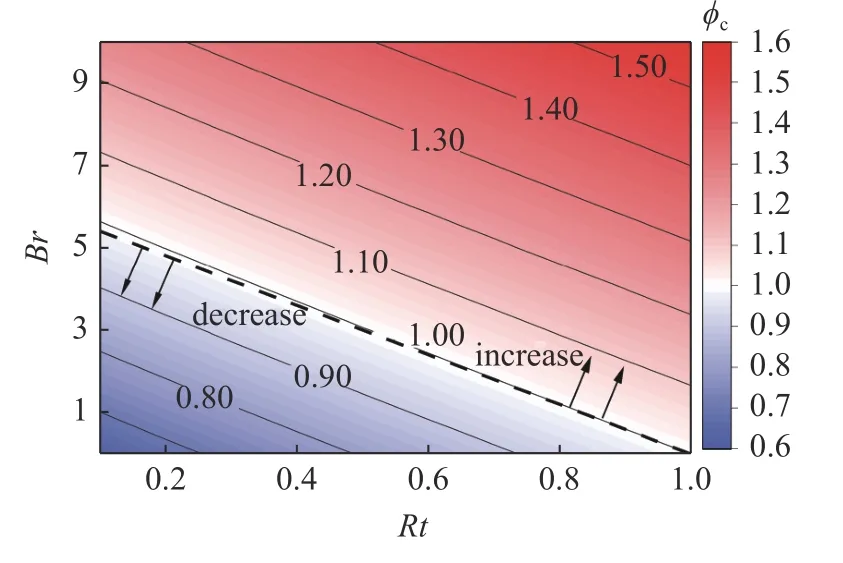
图6 可压缩修正因子 φc 的等值线图Fig.6 Contour map of the compressibility correction factor φc

图7 显示了量热完全气体库埃特流动摩阻和热流的理论预测值与DSMC 计算值的对比图,实线为积分形式的精确数值解式(5),虚线为参考温度方法得到的近似理论解式(11),符号点是DSMC 数值模拟结果,其中实心和空心符号分别表示根据摩阻(式(4))和热流(式(8))结果推出的相应数值.在不同的温度比Rt下,摩阻和热流随剪切强度变化的规律都与预测相符,相对误差在2%以内.

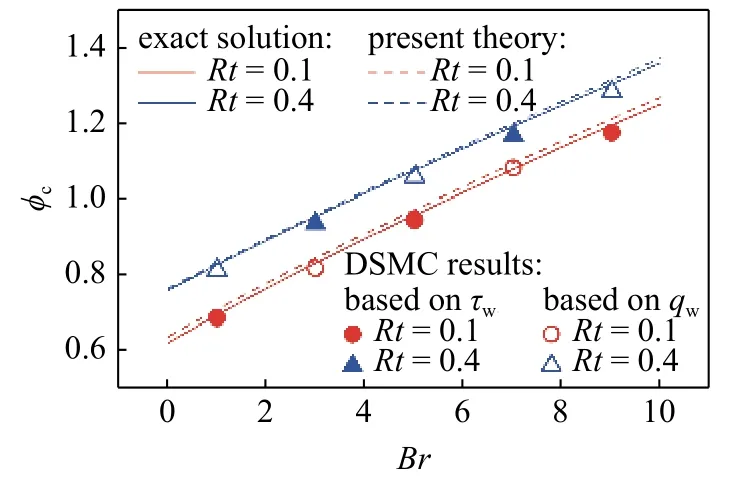
图7 量热完全气体可压缩修正因子近似理论解与精确解和DSMC 数据之间的对比Fig.7 Theoretical prediction of compressibility correction factorφc under calorically perfect gas model and its comparison with the exact solution and DSMC results

2.2 振动非平衡对参考温度的影响

正如前面提到的那样,高超声速库埃特流动除了需要考虑流动可压缩性带来的影响外,还需要考虑流场温度升高引起的高温真实气体效应的影响.对于振动模态激发的热完全气体,库埃特流动的控制方程组为

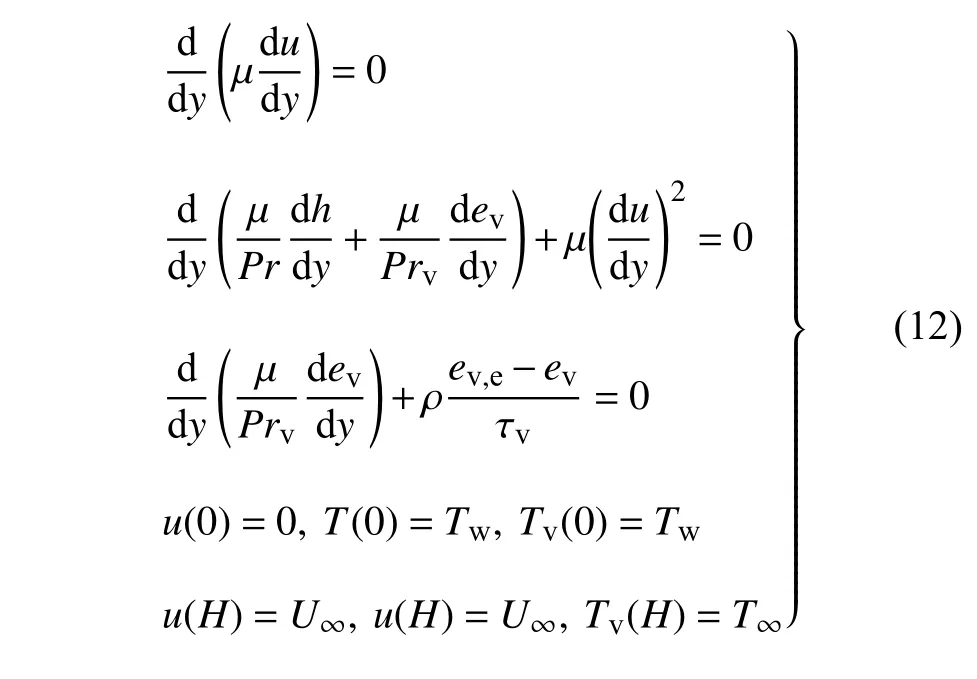
其中,气体平转动模态的焓h=cpT,其中定压比热容cp仍沿用了量热完全气体模型的定义;气体的振动能,其中 θv和R分别是振动特征温度和气体常数(对于氮气,θv=3371K,R=;ev,e是平转动温度T对应的平衡振动能;振动弛豫特征时间[15]τv=C1/p·exp(C2/T)1/3(对于氮气,C1=7.12×10-3atm·μs(1 atm=1×105Pa),C2=1.91×106K).振动能Prandtl 数Prv表征气体动量和振动能输运能力的相对强弱[50].为了找到振动非平衡库埃特流动中的控制参数,对方程进行无量纲化,引入无量纲变换如下

方程中除了表征可压缩效应的控制参数Br和Rt外,还出现了新的无量纲参数.=Pr/Prv表征气体分子平转动模态与振动模态导热能力之比,对于氮气=0.9.Damköhler 数表征振动能导热过程与振动能弛豫过程的特征时间之比,其中 ρH2Prv/μ 衡量了气体分子振动能导热特征时间[51].ηv=(ev,∞-ev,w)/(haw-hw) 表征气体分子振动与平转动模态导热驱动势之比.

特别地,特征参数Dav,r是当前问题中的振动非平衡判据.当Dav,r→0 时,振动趋近于冻结极限;当Dav,r→∞时,振动趋近于平衡极限;当Dav,r～1 时,振动处于非平衡状态.考虑到公式中涉及的热力学参数p和黏性系数 μ 都会随着温度变化,不妨用参考温度对应的不可压缩流动状态来估计,取其参考值p*和.经过整理,振动非平衡判据Dav,r表示为

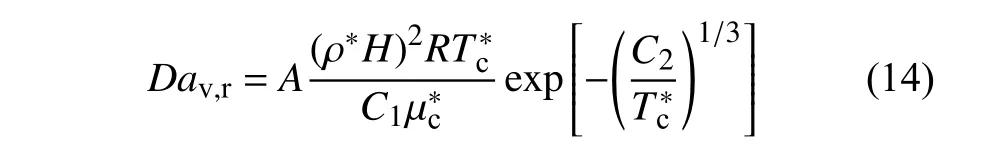
更进一步地,为了赋予Dav,r定量的物理意义,以便预测振动非平衡效应的影响,引入比例系数A,通过后文DSMC 数据可标定A≈0.053 .

气体分子的振动模态激发会使得振动温度升高,平转动温度降低,如图8 所示.气体的热物性参数随平转动温度而变化,为了定量描述这一变化,有必要根据振动非平衡程度对可压缩因子 φc进行修正.

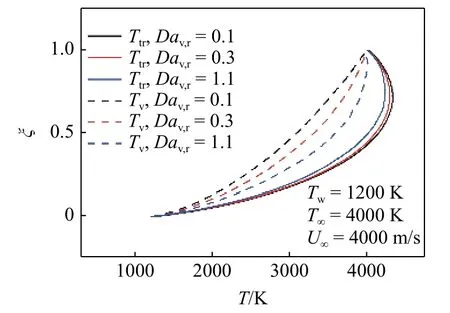
图8 热完全气体可压缩库埃特流动的温度剖面Fig.8 Temperature profiles of the Couette flow of a thermally perfect gas

在振动冻结极限条件下,平转动温度不受振动模态的影响,不需要修正;在振动平衡极限条件下,气体分子的平转动能会最大程度地传递给振动能,此时对热物性参数的影响最大,所以需要先考虑振动平衡极限下的修正.考虑到在等效不可压缩库埃特流动中温度均匀分布,可以根据能量守恒关系得到一种可行的求解振动平衡极限下的参考温度的方法,即

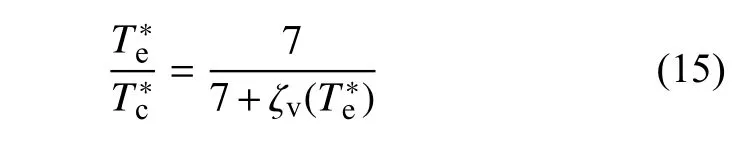
其中,ζv(Tv)=(2θv/Tv)/[exp(θv/Tv)-1] 为气体分子的振动自由度.对于振动非平衡状态,其参考温度介于冻结极限和平衡极限之间.可以发现,冻结和平衡极限的加权平均可以很好地描述振动非平衡状态下的参考温度,即

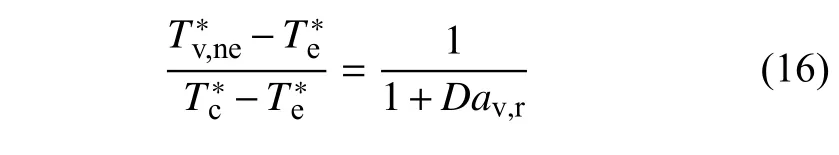
相应的可压缩修正因子为

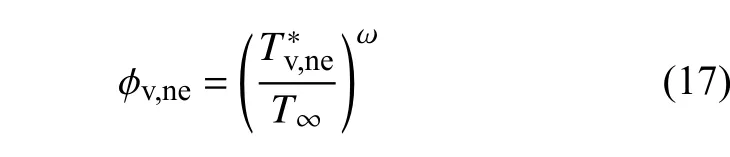
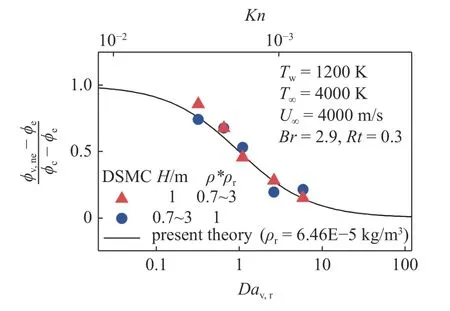
图9 可压缩修正因子随振动非平衡判据的归一化变化Fig.9 Normalized variation of compressibility correction factor with the vibrational nonequilibrium criterion

2.3 振动非平衡对雷诺比拟关系的影响

对于量热完全气体模型,库埃特流动的壁面摩阻系数Cf和Stanton 数S t之间存在雷诺比拟关系(7).对于热完全气体,考虑气体分子振动模态激发后,也能相应得到壁面摩阻和热流之间的能量积分关系

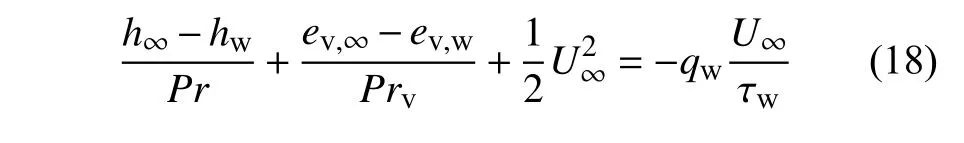
为了更好地体现振动激发对雷诺比拟关系的影响,Stanton 数的定义仍然采用量热完全气体模型的焓差 (haw-hw) 来无量纲化

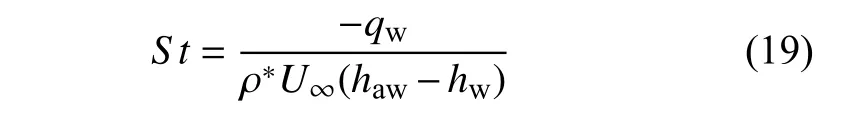
从而热完全气体库埃特流动的雷诺比拟关系为

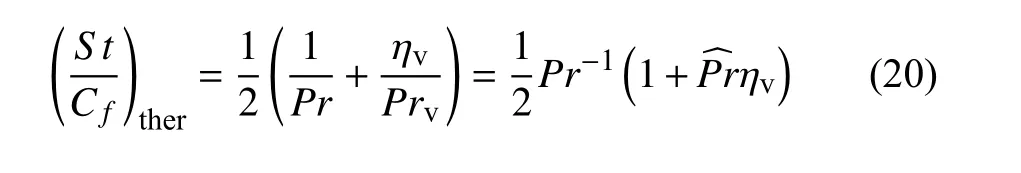
式(20)说明,热流和摩阻之间的比拟关系只与各个内能模态的热流驱动势之比 ηv有关,而与流动振动非平衡程度无关.这是因为,本文假设气体与壁面碰撞过程中,各个模态的能量都完全适应.流场中的能量无论是平转动能的形式还是振动能的形式都能完全地参与壁面热交换过程,在与壁面碰撞过程中各种模态的能量没有差异,总热流只与总的热流驱动势相关.另一方面,由于振动激发引起的气体黏性系数和导热系数的修正是一致的,二者均与温度呈相同幂次关系,在比拟关系中这一影响相互抵消.因此,对于考虑振动激发的热完全气体,由于气体分子振动模态与平转动模态的导热能力有所差异,雷诺比拟关系与总热流驱动势中振动能的占比相关,与流动非平衡程度无关.

图10 中,虚线和实线分别代表量热完全气体和热完全气体的雷诺比拟关系(式(7)和式(20)),符号点表示DSMC 的数值计算结果,空心符号和实心符号代表的算例一一对应,二者流动边界条件完全一致,只有气体模型的差异.从图中可以看出,理论预测的结果与DSMC 数值计算的结果吻合得较好,从而能够验证理论的正确性.

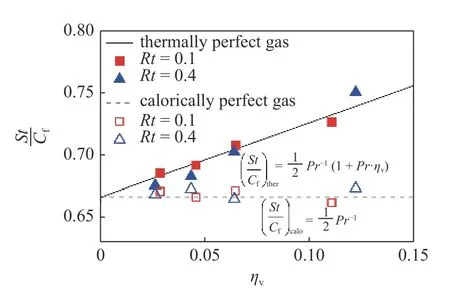
图10 不同气体模型下库埃特流动的雷诺比拟关系Fig.10 Reynolds analogy of the Couette flows under different gas models

2.4 高超声速库埃特流动的摩阻和热流

通过前文的分析可知,在高超声速库埃特流动中,需要考虑剪切流动中上下边界温度差异引起的导热过程、剪切运动造成的黏性耗散过程,以及振动非平衡过程的影响.通过借鉴参考温度方法的思想,气体热物性参数的变化都被归结到无量纲的可压缩修正因子 φ 上.对于量热完全气体,修正因子φc(式(11))只与流动控制参数Br和Rt相关.对于振动激发的热完全气体,振动非平衡的可压缩因子φv,ne需要在此基础上进行二次修正,修正幅度由振动非平衡判据Dav,r决定(式(16)).从而,高超声速库埃特流动的壁面摩阻系数Cf为

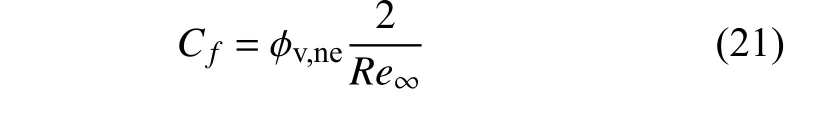
再结合热完全气体库埃特流动的雷诺比拟关系式(20),可求得表征壁面热流的S t数

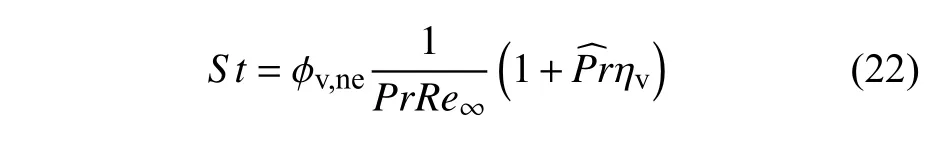
图11 和图12 分别展示了对于高超声速库埃特流动的摩阻和热流的理论预测结果与DSMC 数值结果的对比图.可以看出,无论是量热完全气体还是考虑振动非平衡的热完全气体,在不同的边界条件下的理论预测结果与数值结果都能吻合得较好.说明本文提出的无量纲参数能够很好地描述不同条件下的可压缩效应以及振动非平衡效应,推导得到的参考温度以及可压缩修正因子也能准确地预测高超声速库埃特流动的摩阻和热流.

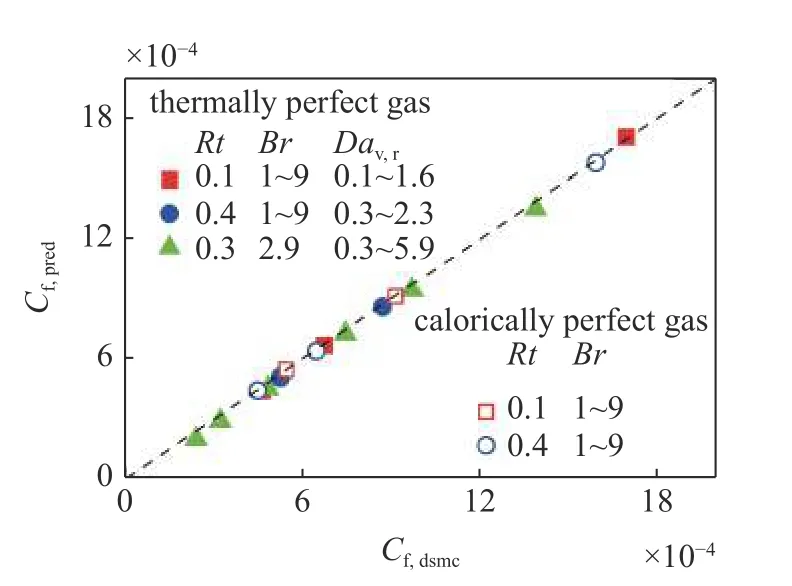
图11 不同条件下库埃特流动壁面摩阻的理论预测和DSMC 数值结果的对比Fig.11 Comparison of the theoretical prediction and DSMC results of the skin-friction of Couette flows

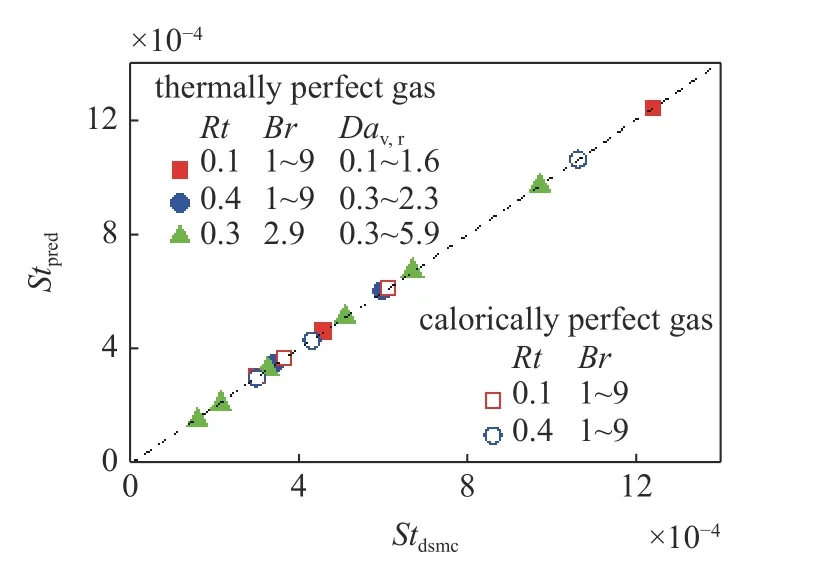
图12 不同条件下库埃特流动壁面热流的理论预测和DSMC 数值结果的对比Fig.12 Comparison of the theoretical prediction and DSMC results of the heat flux of Couette flows

最后需要说明的是,本文上述分析讨论仅适用于近连续区,当流动更加稀薄后,新的流动物理现象会显著影响气动力/热的预测.一方面,稀薄流动中壁面的速度滑移、温度跳跃现象显著,对于参考温度和雷诺比拟关系的影响需要重新考虑[52];另一方面,根据之前的研究结果[31],在流动更加稀薄后,气体分子与壁面碰撞时,平转动模态很快与壁面之间达到平衡,而振动模态往往需要更多的碰撞才能与壁面达到热平衡,壁面上存在振动能适应非平衡过程.这一过程对摩阻影响不大,但对热流影响较为显著,需要提出新的非平衡判据来讨论.可以看到,当考虑极端环境下的复杂介质和复杂边界条件时,即使极为简单的库埃特流动模型,也将表现出丰富且多变的非平衡过程,需留待后续研究中进一步完善.

3 结论

本文以新型高超声速飞行器气动力/热精确预测为背景,研究了高温气体分子振动非平衡效应对典型强剪切流动模型-库埃特流动及其传热特征的影响.通过物理建模与理论分析,提出了高温真实气体库埃特流动的参考温度表达式和振动非平衡判据,进而构建了该流动模型摩擦阻力和热流的理论预测公式,并采用DSMC 数值方法对之进行了验证.研究发现,流动可压缩性和分子振动非平衡效应对于气体热物性参数的影响都可以通过参考温度模型进行修正;对于振动激发的热完全气体模型,雷诺比拟关系仍然成立,只是比拟系数需要考虑振动能传热的影响.通过参考温度方法和修正的雷诺比拟关系可以很好地预测高超声速库埃特流动的气动力/热特征.该研究丰富了对非平衡流动物理的认识,对研究更复杂流动模型的非平衡传热问题及工程快速估算都具有参考价值.