借助于有效的教学模式构建和谐高效的课堂

缪树模

[摘  要] 为了进一步突破应试教育的束缚，培养出具有独创精神的新型人才，在初中数学教学中既要突出学生的主体作用，又要重视教师的主导价值，协调好“教”与“学”的关系，坚持“教”与“学”协同发展，实现教学相长.

[关键词] 主体作用;主导价值;教学相长

在素质教育的影响下，初中数学教学模式、教师手段、教学方法日益丰富化、多样化. “三环三学”的新型教学模式改变了以“传授”为主的教学现状，体现了教师为主导、学生为主体、训练为主线的原则，其有助于提高教学有效性，促进师生和谐发展. 另外，为了使课堂更高效，在课堂教学中可以遵循“五步法”，即“温故知新—自學质疑—细读研学—拓展延伸—总结概括”，进而顺着学生的思维脉络，借助于循序渐进的引导，建构和谐高效的数学课堂. 笔者以“最大利润”为例，展现了“三环三学”教学模式的优势，并在研学环节坚持“以生为主”，借助于“五步法”唤醒了学生的主体意识，取得了较好的教学效果，现在将一些心得体会分享给大家，以期共鉴.

预习环节

预习环节顾名思义就是课前策划，即教师依据教学目标和实际学情设计预习目标，制定预习导学单，根据导学内容既可以帮助学生巩固旧知识，为探究新知识扫清思维障碍，又可以让学生课前就可以对本节的教学重难点形成初步认识，有效提高听课效率. 同时，在预习环节，教师可以鼓励学生进行合作学习，这样通过课堂争辩、交流、合作，学生往往可以总结归纳出许多有价值的资源，不仅可以丰富课堂教学内容，而且有利于发现型、创新型课堂的建构. 可见，课前策划在数学教学中具有重要的价值，是教学的重要组成部分之一，应引起一线教师的高度重视. 当然，要使课前策划能够发挥其特有的优势，教师应以“三个理解”为基础，设计具有针对性和前瞻性的预习内容，从而在明确目标的指引下开展有意义的教学，提升教学有效性.

研学环节

在“利润最大”的研学环节，笔者结合教学内容和具体学情，通过“五步法”充分挖掘学生的内在潜能，引导学生学会自学、学会合作、学会探究，从而轻松地掌握了新知识，实现了新发展.

1. 温故知新

本节内容与生活息息相关，因而在此环节教师可以采用情境引入法，借助于生活问题诱发学生联系旧知识去思考新问题，从而拉近“新”与“旧”的距离，提升学生的学习信心.

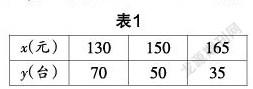
例1  某产品的成本价为120元/台，在试营业阶段，每件售价x（元）与日销售量y（台）的函数关系如表1所示. （日销售量y是每件售价x的一次函数）

（1）写出y与x的函数关系式;

（2）如果你是老板，你会如何给商品定价？

笔者出示第（2）问后，学生的探究热情被迅速激发了，个个争当聪明的老板，课堂气氛活跃了起来. 在此过程中既复习了一次函数解析式的求法，又为接下来二次函数最值的探究做好了铺垫. 这样以生活情境引入新知识“利润最大”的教学自然得体，同时借助于实际应用，更能彰显数学学习的价值.

2. 自学质疑

为了引导学生能够自己总结归纳出一些有价值的东西，在此环节教师可以列举一些具体的题目，引导学生在解决问题的过程中理性地认识问题规律，培养学生自主发现、自主探究的优良学习品质.

例2  某商品的进价为10元/件，售价为15元/件，则每件商品的利润是____元.

（1）若涨价2元，则售价为____元，利润为____元;

（2）若涨价3元，则售价为____元，利润为____元;

（3）若涨价x元，则售价为____元，利润为____元;

（4）若降价x元，则售价为____元，利润为____元.

设计意图  借助于简单的生活实例引导学生总结归纳出利润与成本和售价的对应关系.

例3  某商品原来每天可卖出100件，为了获得更高的利润，经市场调研发现：若该产品每降价1元，则多卖出2件;若每涨价1元，则少卖出2件.

（1）若每降价2元，则多卖出____件，日销售量为____件;

（2）若每降价x元，则多卖出____件，日销售量为____件;

（3）若每涨价5元，则少卖出____件，日销售量为____件;

（4）若每涨价x元，则少卖出____件，日销售量为____件.

设计意图  引导学生总结归纳出总利润与销售量和单件商品利润的对应关系.

这样通过简单的、熟悉的问题引导学生总结归纳出了本节课两个重要的等量关系，为后面“最大利润”的探究做好了充足的准备.

3. 细读研学

在此环节，先在教师的带领下，借助于典型的例习题的示范功能帮助学生理清知识要点，解除心中疑惑，形成解题规范;接下来让学生独立完成一定量的基础练习，通过“练”让学生发现问题，并通过合作交流或教师点拨解决问题，以此既能引导学生独立思考，又能让学生在互帮互助中不断提升自己、发展自己，从而让每个学生都能有所收获.

例4  某商品进价为40元/件，现售价为60元/件，每周的销售量为300件，根据市场调研发现，若每涨价1元，则每周少卖10件.

（1）写出销售利润y（元）与涨价x（元）的函数关系;

（2）当涨价x（元）为何值时，销售利润y（元）最大？最大利润是多少？

（3）最终售价为多少元时，可以使得销售利润y（元）最大？最大利润是多少？

有了前面例题的铺垫，例4对于学生来说并不陌生，可以引导学生先独立思考，这样可以在“研学”的过程中渗透“验学”. 学生的基本思路形成后，教师可以带领学生共同完成问题的解决，在此环节要充分展示学生的思维过程. 为了使沟通更有效，教师可以将问题改编成问题组，使之转化为学生熟悉的内容. 如先让学生思考“涨价2元时，卖出的商品件数与销售利润的关系”，接下来按照这个思路探究“涨价x（元）时，销售利润y（元）与涨价x（元）的函数关系”，这样通过循序渐进地引导帮助学生深化新知识的理解.

设计意图  借助于例题趁热打铁，通过例题的精讲帮助学生形成解题规范，加深学生对新知识的理解，同时引导学生学会用新知识去解决实际问题. 以上三个问题由易到难，层层递进，是在学生原有认知基础上的建构，符合学生的认知发展规律，有利于提升课堂有效性.

4. 拓展延伸

学生通过以上环节理解并应用了新知识，为了进一步强化理解，教师可以充分发挥变式练习的拓展延伸的功能，借助于“变”培养思维的灵活性，实现知识的融会贯通.

例如，对于例4，可以将“涨价”变为“降价”，将“少卖”变为“多卖”，让学生在解决实际问题的过程中进一步理解“总利润=销售量×每件利润”，进而将知识点有效地串联起来，提升实际应用能力.

5. 總结概括

总结概括可谓是一节课的点睛之笔，在此环节引导学生将点滴的收获总结归纳为学习经验，这样不仅可以帮助学生理清本节课的重难点，而且通过有效的回顾可以加深对知识的理解. 另外，在此环节还可以引导学生通过相似、相关问题的联想，将新知识纳入原有的知识体系，实现认知的完善与优化.

当然，“五步法”并非一成不变，在实际教学中还是需要教师结合具体的学情和教学内容进行适当的调整，不过无论如何调整都应协调好“教”与“学”的关系，要注意把握课堂的灵活性、创新性.

验学环节

1. 回归课本，总结升华

经历了预习环节和研学环节，为了进一步帮助学生升华所学，教师可以随堂进行检测，当然题目的设计应遵循“低起点、小坡度”的原则，这样既能驱动每个学生解决问题，又能让学生提升不同程度的应用能力，实现“稳中求进、差中求异”的效果.

2. 优化知识，拓展提升

在学习中既要回归课本，掌握“双基”，又要跳出课本，带领学生回归生活，从而让学生体验“学以致用”的真谛，以此优化学生的知识结构，提升学生的数学应用能力. 在此环节，教师设计检测试题或作业时不能拘泥于课本，而应结合学生的实际生活设计一些符合学生认知的问题，以此让学生在“吃得饱”的基础上“吃得好”，通过新拓展实现“优中求精”的目的.

3. 多元评价，激发热情

在研学环节，教师应结合实际学情、教学内容、课堂表现给予学生准确的、及时的评价，侧重发挥课堂评价的激励作用，以此提高学生的自信心，提升其数学学习兴趣. 其实，研学环节往往渗透于“预习”和“研学”中，贯穿教学始终，通过巧妙的“验”可使“教”与“学”变得更高效.

总之，在实际教学中，要改变传统的教学观念的束缚，重视发挥学生的主体作用，让学生在“活动”中学习，在“探究”中提升，在“合作”中成长，进而营造一个和谐高效的数学课堂.

3935501908210