大惯量低刚度转台的扫描控制
蔡彦博,杨德振,2
(1.华北光电技术研究所,北京 100015;2.北京真空电子技术研究所,北京 100015)
1 引 言
近年来随着隐身技术的发展,机载雷达对隐身飞机的探测难度日趋增大。因此,机载红外搜索跟踪系统的作用日趋重要。随着现代战机性能的不断提升,为应对日趋复杂的空战态势,要求红外搜索跟踪系统扫描速度快、周期短、效率高。故要求系统在短时间内具有较大加速度及较快的调整能力[1-4]。
红外搜索跟踪系统转台受机载环境限制,大多需采取轻量化设计,其结构均为薄壁中空的大框架结构,具有结构刚度弱的特点。同时,系统内部需安装各种光学镜片及光电传感器设备,系统惯量大。为保证转台加速过程中的快速性及稳定性,为了保证快速扫描提高扫描效率,缩短启动时间,要求控制曲线在启动过程中平滑过度无突变,即要求转台启动过程中足够平稳无冲击[1-4]。为保证转台加速过程中的快速性及稳定性,减小转台启停时的冲击和振动,本文提出了基于五次曲线控制函数的加减速控制算法。
2 搜索转台的关键算法
搜索转台是红外搜索跟踪系统的关键部件,通过驱动和控制扫描光机系统进行水平和垂直方向的运动,来实现对整个搜索空间的覆盖,将外界能量引入红外探测器进行成像。其中水平运动由方位搜索转台控制,其结构如图1所示,整个搜索转台由无刷电机、光电编码器、光学系统、轴承、基座及控制器组成,光学系统、光栅尺、及电机转子组成转动部件,电机、读数头及基座组成固定部分。由控制器对电机提供驱动信号,带动转动部件进行周期往复运动实现系统的扫描成像。方位搜索转台响应的快速性决定了系统的扫描周期,速度的稳定性决定了系统的成像质量。良好的启停控制算法正是保证响应快速性与速度稳定性的关键。

图1 搜索转台框架结构示意图
加减速控制在扫描控制系统的研究中至关重要,国内外对其进行了长时间的研究,郭新贵等[5]提出的线性(直线)加减速控制算法资源占用量最小,在光机一体式搜索转台中应用最多,但其在加减速过程中加速度不连续,存在突变点,对于低刚度转台系统,极易发生振动、超调。由于加速度不连续带来的换向冲击,多次作用后容易导致转台内的光学镜片松动。李明等[6]提出的正弦加减速控制曲线,无限阶可微分,可以实现加减速过程中速度、加速度、加加速度平滑过度无突变。但其构造函数较为复杂,计算量较大,占用硬件资源较多,故在控制系统中较少使用。陈友东等[7-10]提出的S曲线加减速控制算法经过改进后,其加加速度可实现平滑过度无突变,但该算法需进行多段参数规划,设计过程复杂,不太适用于机载控制系统。本文提出了一种基于五次曲线控制函数的加减速控制算法,构造函数简单、加加速度可平滑过度无突变,可有效减小对结构的冲击,适用于机载控制系统。
3 大惯量低刚度下的扫描加减速控制
3.1 线性(直线)加减速控制算法分析
假设各阶段的运动轨迹数据生成方式均是通过数学积分方式生成,即角速度的积分为行程(位移)、角加速度的积分为角速度、角加加速度的积分为角加速度,则转台加减速过程中各参数的数学表达式如下:
(1)
式中,s0,ω0,ε0分别为行程、角速度与角加速度的初始值;s(t),ω(t),ε(t),j分别为行程、角速度、角加速度、加加速度在t时刻的实际值。作为扫描控制系统中计算量最小,行程规划方式最简单的斜坡加减速控制算法,其在各种加减速控制系统中得到了广泛的应用。斜坡加减速控制算法其速度函数为连续曲线,但加速度函数为间断函数。线性加减速控制过程整体分为三部分:启动加速段、匀速扫描段、减速停止段。线性加减速控制算法的函数曲线如图2所示。
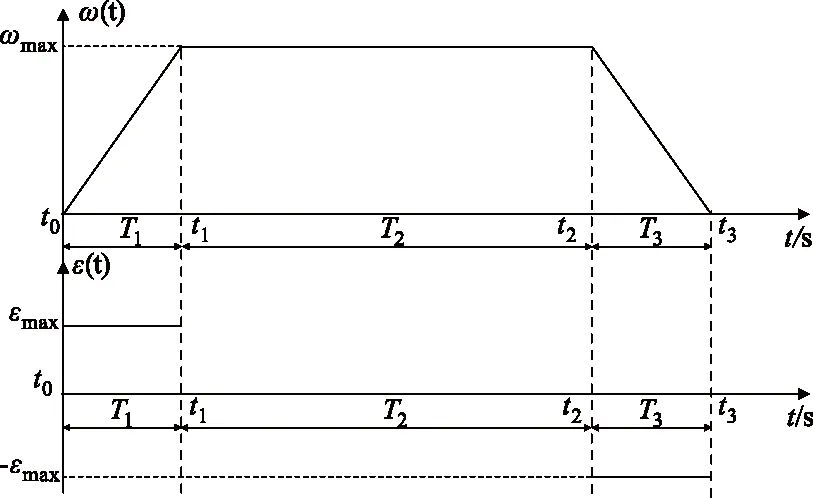
图2 线性加减速控制曲线角速度及角加速度示意图
如图2所示,加速段时间T1=t1、匀速段时间长度T2=t2-t1、减速段长度T3=t3-t2。在t1时刻,转台速度达到指定速度,由图2分析可知,当转台达到指定速度后加速度直接给定为0,故转台加速度存在突变,未能进行平滑过度。可能会对结构造成柔性冲击,并造成控制系统的超调。
3.2 五次曲线加减速控制算法分析
对于扫描控制系统,角速度曲线的五次曲线构造函数可写为如下形式:
ω(t)=k5t5+k4t4+k3t3+k2t2+k1t+k0;t∈[0,tk]
(2)
式中,tk为转台启动加速的时间。对式(2)依次进行微分可分别得到角加速度ε、角加加速度j的函数表达式如式(3)所示:
(3)
为保证转台加速过程中角速度、角加速度及角加加速度能够平滑过渡并且使其变化过程连续无断点,使得转台在整个加速过程中,不会对机械结构造成冲击,避免对结构件造成损伤,五次曲线控制函数需要满足以下边界条件:
(4)
式中,ωmax为转台加速到终点时的角速度,即系统扫描工作时的正常转速。
将式(4)中所示的边界条件代入式(2)、(3)中,可得到用于求解五次曲线控制函数中各项系数的线性方程组如式(5)所示:
(5)
通过式(5)解得各项系数结果为:
(6)
将式(6)中解得的各项系数代入式(2)、(3)中可得:
(7)
对式(5)进行积分可得转台加速过程中的行程(位移)曲线函数s(t)为:
s(t)=k5t6/6+k4t5/5+k3t4/4+k2t3/3+k1t2/2+k0t
(8)
代入式(6)中的结果可得行程(位移)曲线函数s(t)的最终表达式为:
(9)
根据式(7)、式(9)可得五次曲线加减速控制函数的位移、角速度、角加速度、加加速度函数曲线如图3所示。

图3 五次曲线控制函数位移、角速度、角加速度、加加速度函数曲线示意图
4 实验分析
本研究使用的搜索转台采用永磁同步电机(PMSM)作为驱动电机,通过读取编码器反馈的位置信息差分解算获取系统响应曲线,并通过Matlab画图示意;同时为了直观展示所提算法优越性,实时采集伺服搜索运动对应时刻的红外成像效果进行演示。
4.1 控制系统响应曲线比较
首先对采用线性加减速控制算法设计的控制程序进行测试,设置系统工作条件为:T1=T3=0.1 s,ωmax=60°/s、ωmax=120°/s系统采样结果如图4和图5所示。

图4 采用线性加减速控制算法以60°/s扫描时系统速度采样图
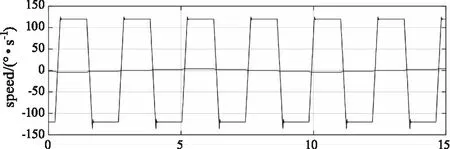
图5 采用线性加减速控制算法以120°/s扫描时系统速度采样图
从图4和图5中可以看出,在系统加速终点及减速换向时,系统出现明显过冲,对结构产生较大冲击。且系统超调较为明显,为最大速度的13.5 %,系统的稳定性及速度平滑性明显下降。
下面对采用五次曲线加减速控制算法设计的控制程序进行测试,设置系统工作条件为:T1=T3=0.1 s,ωmax=60°/s、ωmax=120°/s系统采样结果如图6和图7所示。

图6 采用五次曲线加减速控制算法以60°/s扫描时系统速度采样图
从图6和图7中可以看出,在系统加速终点及减速换向时,系统状态平滑过渡,未对结构造成明显冲击。系统由加速至稳速过程中速度平滑无超调,系统的稳定性及速度平滑性明显优于线性加减速控制算法,在100 ms时间内能够由静止加速到≮100°/s、且速度误差不大于0.1 ‰。
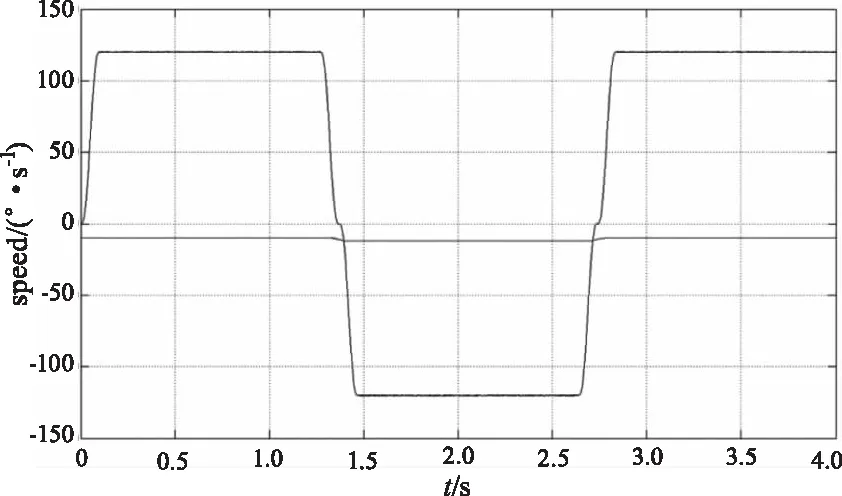
图7 采用五次曲线加减速控制算法以120°/s扫描时系统速度采样图
4.2 系统扫描成像效果比较
利用实验室的光学特征靶标对系统进行了动态扫描成像试验,选取扫描有效区域边界的图像作为对比,图8(a)、图8(b)为采用线性加减速控制算法分别在有效区域左侧和右侧边界采集到的红外靶标成像效果,图9(a)、图9(b)为采用S曲线控制算法于有效区域左侧和右侧边界采集到的红外靶标成像效果,图10(a)、图10(b)为采用本文提出的五次曲线控制算法于有效区域左侧和右侧边界采集到的红外靶标成像效果。

图8 使用线性加减速控制算法于有效区域左侧和右侧边界采集到的红外图像

图9 使用S曲线加减速控制算法于有效区域左侧和右侧边界采集到的红外图像

图10 使用五次曲线加减速控制算法于有效区域左侧和右侧边界采集到的红外图像
从图8~图10可以看出,线性加减速控制算法所造成的速度超调已严重影响到了系统的成像质量,使系统的有效扫描区域下降。采用S曲线加减速控制算法时,成像效果已有明显改善,但因S曲线加加速度仍不连续,在速度变化较快时,图像依然存在拖影。而采用五次曲线控制算法的系统响应在边界区域平滑,系统能够正常清晰成像。有效提高了系统对弱小目标的检测成功率。
5 结 论
为满足大惯量低刚度搜索转台,扫描控制过程中能够平滑过渡的要求。本文阐述了基于线性(直线)变速控制与基于五次曲线变速控制的算法原理,对比了系统的响应结果。由于线性(直线)加减速控制算法在加速终点及减速换向时角加速度存在突变,会对系统结构造成较大冲击,并造成系统角速度的较大超调。而五次曲线加减速控制算法,而五次曲线加减速控制算法在整个工作过程中角速度及角加速度均能平滑过渡,有效减小了由加减速过程对系统带来的冲击和振动,故五次曲线加减速控制算法更适用于大惯量低刚度转台的加减速控制。

