一种三维激光雷达系统标定方法

李树青,邢鑫龙,林靖宇

(1.柳州柳工叉车有限公司,广西 柳州 545005；2.广西大学电气工程学院,广西 南宁 530004)

1 引 言

目前,物流搬运行业仍处于半自动化的阶段,主要还是通过人工驾驶叉车来完成物料的运输与堆放,车辆驾驶作为需要高度集中注意力的工作,长时间的驾驶必定导致司机的疲劳,不但降低了工作效率,还将埋下安全隐患；同时还降低了车辆的利用率,增加设备的持有成本。因此,研究并实现智能无人化的叉车就是解决行业痛点的必由之路,但要实施智能无人化作业,必须精确地确定待搬运物料的尺寸及位置,所以提高物料尺寸及距离的测量精度是其核心关键技术之一,如图1所示,当无人化叉车的作业目标是把A物料搬运到C物料之上时,其必须精确测量得到A,B,C物料的尺寸大小,还有叉车距离A,B,C物料的距离及物料之间的相对距离。

图1 叉车搬运示意图

常用的物料尺寸测量技术分为基于视觉的测量技术和基于激光测距的测量技术[1-2]。视觉测距系统由于其测量精度不高,且受恶劣天气和光照等环境因素影响较大,因此不适合用于物流搬运行业的物料尺寸的测量。激光测距系统由于其快速,高精度、环境适应性强等特点,在各个领域得到了大量的应用[3-6]。为了提高精度和效率,很多研究者使用二维激光雷达和伺服系统来搭建三维激光雷达系统,在大部分方案中,他们的伺服系统都是旋转平台的转轴处于二维激光雷达的扫描平面中[7-9],其他方案包括设计一个云台并使其有规律的摆动[10],使用弹簧让其自由的振动[11],使旋转轴和扫描平面倾斜某个角度[12-13],但这些方案都没有改进目标物体被遮挡的问题。同时,很多学者对激光雷达的标定进行了研究和改进,上海交通大学俞奇奇等人[14]提出通过固定激光雷达在特定位置,使得标定参数减少到一个,并使用墙面作为标定板来完成参数的标定。其分别在两个位置对同一墙面进行扫描,根据几何关系,很容易计算得到标定参数。但该方法忽略了激光雷达中心到旋转中心距离存在着装配和制造误差,只是通过参阅手册默认此值已知,同时特定位置的要求限制了激光雷达的扫描范围。王春梅等人[15]提出首先建立转换矩阵,再采取代入特殊解的方法求解此转换矩阵,以此标定激光雷达的系统参数。通过选取四个特殊点(三平面的交点,三个坐标轴上各取一个特殊点),代入求解转换矩阵即可。该方法同样也忽略了激光雷达中心到旋转中心距离存在着装配和制造误差,只是通过参阅手册默认此值已知,同时特殊点的测量使得单次测量误差对标定的影响过大,多次测量又会影响标定的效率。

2 系统设计

本文提出的长臂三维激光雷达系统由一个二维激光雷达,一个单轴云台和一个长臂支架组成。长臂支架被安装在云台上使得它可以在水平方向上旋转,而二维激光雷达被安装在长臂支架的另一端并使得它可以进行竖直方向的扫描。由于长臂的作用,使得此激光雷达系统具有很强的抗遮挡性,且长臂的长度可随时调整以适应现场作业的要求。此原型系统如图2所示。

图2 长臂三维激光雷达原型系统

系统坐标系的定义如图3所示,假设这个三维激光雷达是水平放置的,定义云台的旋转轴为z轴,竖直向上为正。xOy平面是水平的并通过二维激光雷达的中心点OL,而且和z轴相交于系统原点O。长臂支架的长度设为R,即O到OL的距离。

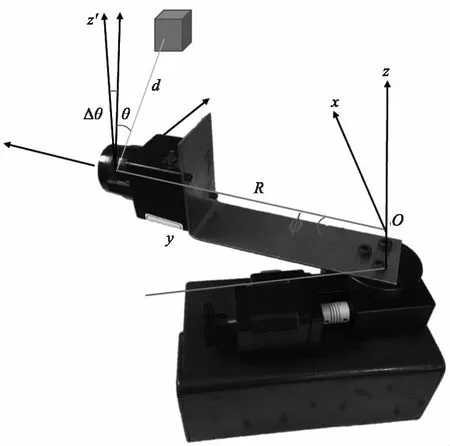
图3 坐标系定义

二维激光雷达坐标系定义如下,原点为二维激光雷达的中心OL,OOL为yL轴,扫描平面为xLOLyL平面,zL轴为二维激光雷达正前方向。需要注意的是,由于装配的误差,zL轴可能不是严格和z轴平行的,这个zL轴和z轴的误差夹角被定义为Δθ。上述符号定义都被列在表1中。

表1 三维激光雷达系统的参数定义

在扫描时,云台旋转使得yL轴转过一个角度φ,这表示云台的标度,之后二维激光雷达扫描竖直平面并获得一行距离数据{d,θ}。这些数据能通过如下转换公式转换得到空间点坐标:

(1)

需要注意的是系统参数R和Δθ在公式(1)中是未知的常数。

3 系统标定

由于二维激光雷达的中心OL不可能通过物理方法到达,所以通过直接测量的方法来精确测量它们是不可能的。对长臂三维激光雷达的系统参数(长臂长度R和二维激光雷达的安装误差角度Δθ)进行精确标定是非常有必要的。本文提出了一种通过扫描平面标定板并用扫描数据求解方程的方法来测量它们。为了降低求解难度,通过解耦合的方法,先标定Δθ,再标定R。而拟合直线和平面重合的方法也使得测量误差得到很好的消除。

3.1 标定Δθ

为了求解Δθ,需设置一块标定板位于三维激光雷达正上方,并使用水平仪保证它们都处于水平位置。几何关系如图4所示。

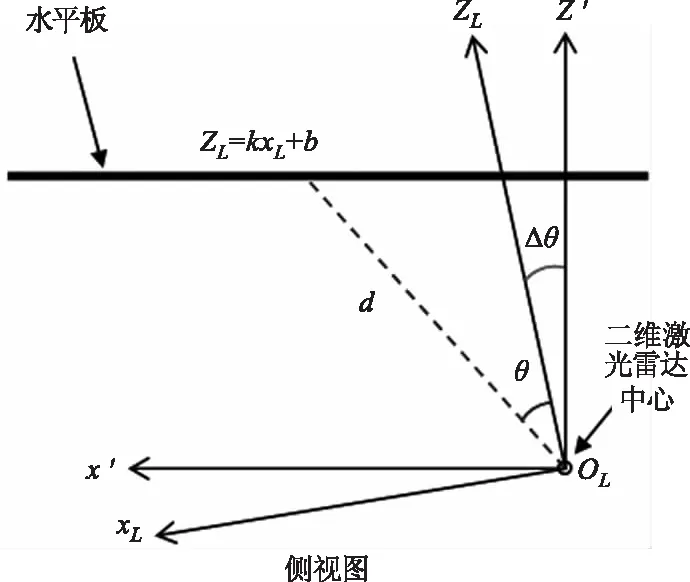
图4 Δθ标定几何原理图

在任意一个云台的位置φ,三维激光雷达扫描标定板并得到一组点,而这些点都位于同一条直线上,直线公式如下:

zL=kxL+b

(2)

其中,zL=dcosθ,xL=dsinθ,而k=tanΔθ和b是未知的。

在采集到的数据中求解k,b是一个简单的直线拟合问题。为了找到一个鲁棒性更好的解法,通过旋转云台的角度φ到多个位置,并取得多个扫描数据,而这些数据都满足公式(2)。当求解出k后,有Δθ=tan-1k。

3.2 标定R

式(1)表明x和y都同R是线性的。因此当R变化时,标定板上的扫描数据点仍然会处于同一个平面上,但是这个平面的位置会相应的移动。所以R不能通过把扫描数据拟合成平面的方法来求解。本文提出了一种通过从相对的视角找到两个相同的面的方法来求解R。详细的数据选取方法见图5,步骤如下文所述。

图5 标定R几何原理图

首先设置三维激光雷达水平而且标定板竖直,之后驱动云台旋转至少180°并使得二维激光雷达的左右两侧都扫描到标定板,最后分离出扫描数据中对应两侧的数据集{d1,θ1,φ1}和{d2,θ2,φ2},分别对应θ1>0 和θ2<0。

这两个数据集满足同一个平面方程:

Ax+By+Cz=1

(3)

把公式(1)代入公式(3),得：

A(K1+RK2)+B(-K5+RK3)+CK4=1

(4)

其中,K1=dsin(θ+Δθ)cosφ,K2=sinφ,K3=cosφ,K4=dcos(θ+Δθ),K5=dsin(θ+Δθ)sinφ。

如果R是已知的,那么求解A,B,C就是一个简单的线性拟合问题。

标定的目的是找到使得从数据{d1,θ1,φ1}求得的平面A1,B1,C1和从数据{d2,θ2,φ2}求得的平面A2,B2,C2重合的R的值。最后,定义两个平面的平方误差为:

E=(A1-A2)2+(B1-B2)2+(C1-C2)2

(5)

之后通过误差下降算法求解此最小值问题R*=argminRE,具体步骤见算法1。

算法 1 标定R

Algorithm 1:Calibration ofR

---------------------------------------------------------

输入:

{d1,θ1,φ1} - 标定版上的扫描数据1,

{d2,θ2,φ2} - 标定版上的扫描数据2,

Δθ- 已标定的参数,

ε- 最小误差。

输出:

R- 标定参数。

步骤:

1:初始化λ=0.1,R=-λ,E(0)=1×106,t=0。

2:计算R=R+λ,t=t+1。

3:求解式(5),从数据{d1,θ1,φ1}得到A1,B1,C1,从数据{d2,θ2,φ2}得到A2,B2,C2。

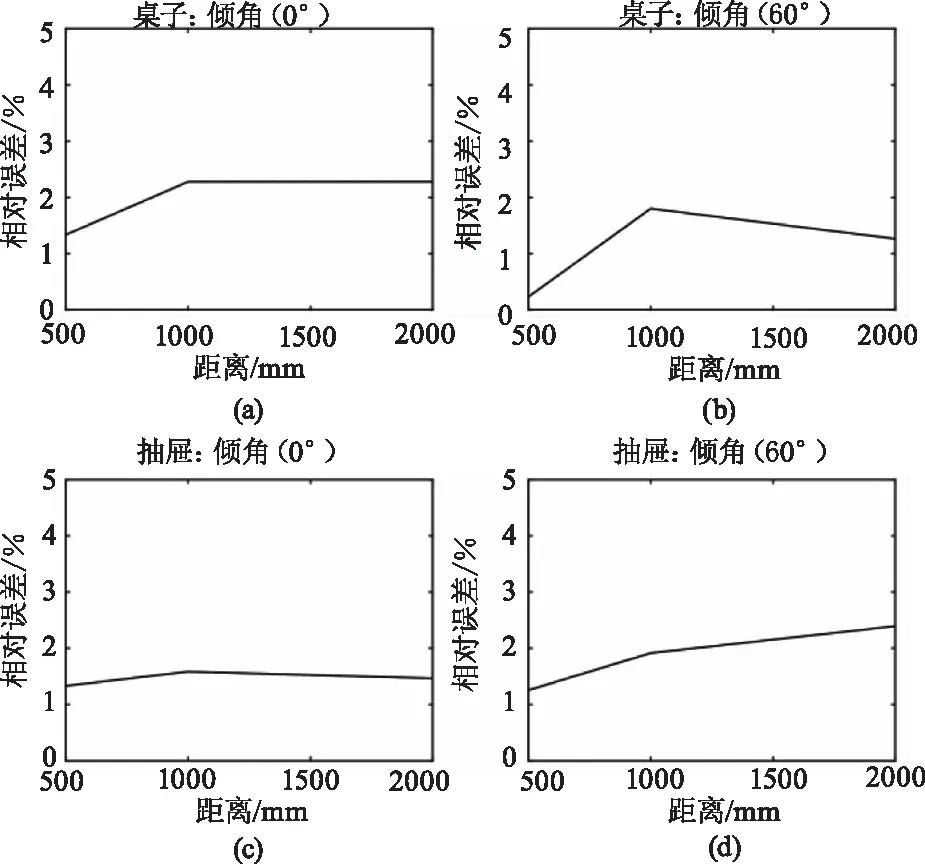
4:使用式(6)计算误差E(t).如果E(t)

5:使λ=-0.618×λ。如果|λ|>ε,返回步骤 2。

6:输出R并停止。

应用上述算法来标定系统参数:第一步标定Δθ,第二步标定R。

在第一步中,使用实验室天花板作为水平标定板,并使用水平仪来保证激光雷达水平放置。从采集到的数据求解得Δθ=-2.3634°,而天花板的高度是2.2793 m。直线拟合的均方误差为0.008136 m。

在第二步中,我们使用竖直的墙面作为标定板。使三维激光雷达对墙面进行180°的扫描,把扫描数据切分成数据集1(φ∈(326.4°,359.8°),θ∈(-88.2°,-60.1°))和数据集2(φ∈(157.7°,204.1°),θ∈(70.0°,91.1°)),这两个数据集对应墙面的同一个区域。最终通过误差下降算法求解得到R=0.1713 m,而这两个面的拟合平方误差为E=10-13.4,如图6所示。

图6 代价函数迭代图

使用标定参数Δθ=-2.3634°和R=0.1713 m,通过公式(1)转换后得到标定环境的点云如图7所示。假如系统参数不准确,重叠区域的点将会分离开来,而在图7中,所有的相同位置的区域都能准确的重叠并且使得重叠区域更加密集,说明标定参数准确可靠。

图7 标定环境的点云数据

4 实 验

在本文的三维激光雷达原型系统中,使用的二维激光雷达型号为Hokuyo URG04LX-UG01,它的角分辨率为0.36°；云台由角分辨率为0.02°的旋转平台和分度高达128的驱动电机组成,而且φ角能直接通过电机驱动程序读取。

通过实验研究改长臂激光雷达扫描系统在不同距离和不同角度时对物体尺寸的测量精度的影响。实验条件如下:两个不同尺寸的物体(宽度为0.048 m的椅子脚和宽度为0.15 m的抽屉),三种不同的距离(500 mm,1000 mm和 2000 mm)和两种不同的倾斜角度(0°和60°)。实验结果如图8所示,此长臂激光雷达扫描系统即便距离增大到2000 mm,扫描的相对误差也没有超过2.4 %。结果表明此系统的扫描精度并未随距离增大而变差且和物体的角度对测量结果的影响也不大。

图8 扫描精度实验结果

最后,我们对随意放置在激光雷达周围的物体分别用进行尺寸测量,并对比测量精度,三次实验的结果如表2所示。可知,在所有的测量结果中,扫描的结果都很精确,最大相对误差不超过3 %,加粗部分的扫描结果误差不超过1 %,而实验3的2号物料的扫描结果基本可以认为得到了此物料的真实尺寸值。

表2 尺寸测量结果

5 结 论

本文为解决无人化叉车在运行中对物料的尺寸及距离的高精度测量要求,设计了一种由二维激光雷达和步进电机云台组成的三维激光雷达扫描系统,并提出了相应的标定方法。该标定方法无需使用特定的标定工具和精密仪器,简单易实施。最后的实验结果表明,此标定方法简易有效,且能达到很高的测量精度要求,满足叉车无人化作业要求,具有很强的实际意义和应用价值。