基于无退化混沌系统的序列密码研究

赵 亮 赵 耿, 马英杰

1(西安电子科技大学 陕西 西安 710000)2(北京电子科技学院 北京 100070)

0 引 言

自1963年Lorenz发现第一个混沌系统以来，混沌已经被许多研究者广泛研究。随着研究的深入，人们逐渐认识到混沌运动的重要性。人们还发现混沌有许多实际应用，如安全通信、化学反应、神经网络和经济学。当混沌是有害的时，人们需要混沌控制来抑制甚至消除混沌；相应地，当需要混沌时，需要混沌反控制来增强混沌，使系统完全混沌。

在混沌系统的众多特征中，正Lyapunov指数的个数和系统全局有界是两个应用广泛的混沌判据，Lyapunov指数是不定维空间中相邻运动轨道平均指数发散强度的一种数值特征，具有多个正Lyapunov指数和唯一正Lyapunov指数的混沌吸引子相比，超混沌吸引子同时向两个或多个方向扩展[1-3]。对于一个离散的混沌系统，当这个系统的正Lyapunov指数的个数等于系统维数，并且系统全局有界时，可以称其为无退化混沌系统。但在连续混沌系统中，需要同时配置正、负和零的Lyapunov指数，所以要保证其Lyapunov指数中有一个为零，一个为负，其余全部为正，并且系统全局有界，这样就可以称其为无退化混沌系统。无退化混沌系统的各方面特性远优于存在退化的混沌系统，这也是众多学者研究无退化混沌系统的原因。

混沌系统的退化可能直接影响混沌加密系统的安全性[4]。目前，解决这一问题的方法有多种，对于连续时间混沌系统，主要包括状态反馈控制方法[5-6]、试错法[7]、弱耦合技术[8-9]和参数扰动[10]。虽然已经提出了一些相关的方法来解决一些连续时间混沌系统的产生问题，但大多数方法仍然遵循传统的试错法。该方法很难设计出高维混沌系统，也不能从理论上真正解决这一具有挑战性的研究课题。

文献[11]提出了一种配置多个正Lyapunov指数的方法，其通过给定受控系统的基础上加入控制器，改变该受控系统的雅可比矩阵，该方法实现的目标就是使受控系统的正Lyapunov指数的个数达到最大，得到无退化的混沌系统。文献[12]提出了一种对受控系统加入控制器得到高维无退化混沌系统的方法，该方法给定一个矩阵，通过对其相似变换得到想要的受控系统。由于受控系统是所给出的指定系统，对于每个维度，受控系统是同一个系统，即对于任给一个受控系统，该方法将不能适用。本文提出了一种新的Lyapunov指数配置方法，对于全局有界系统，根据Shilnikov定理，配置零和负Lyapunov指数很容易[13-17]，当系统的特征值具有r(r≤2)个正实部时，系统将能够产生r个正Lyapunov指数[14-17]。对于任意的受控系统，通过引入两个控制器，改变受控系统雅可比矩阵，配置系统矩阵的特征值与相对应的特征向量来配置正Lyapunov指数的个数，使系统的正Lyapunov指数个数达到最大，从而达到系统无退化的目的。因为本文方法对于任意受控系统都能适用，故相比文献[11-12]方法通用性更强。

1 系统的超混沌系统配置方法

对于如下一个n维的连续时间线性系统：

(1)

(2)

接下来，本文设计了一个线性反馈控制器Bx，使得控制系统的原点为一个渐近稳定的不动点；以及设计了一个合适的非线性反馈控制器f(σx,ε)，使得控制系统能够产生无退化的混沌行为:

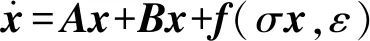
(3)

Bx是一个线性反馈控制器，其中矩阵B为：

定义设A是n阶方阵，如果数λ和n维非零列向量x使关系式Ax=λx成立，那么这样的数λ称为矩阵A特征值，非零向量x称为A的对应于特征值λ的特征向量。

Ax=λx也可写成(A-λE)x=0,它有非零解的充分必要条件是系数行列式|A-λE|=0，即:

这意味着对于式(1)中给定n的阶方阵A，要配置指定的特征值，只须将矩阵A中n(n-1)个元素和给定的特征值λ1、λ2、…、λn代入上式，剩下的n个元素作为未知量，就可以得到一组方程，如下所示：

(4)

这个n维方程组中有n个未知数，因此一定有解，求解这个方程组可以得到剩余的n个元素，并用这些n个元素替换A中相应的元素，得到具有指定特征值的矩阵。

如上所述，矩阵的所有特征值都可以配置为任意值。因此，控制器Bx可以用来配置A+B的特征值，使得Ax+Bx的原点是渐近稳定的不动点。接下来，令：

(5)

假设控制器只包含一个非线性函数。考虑到耗散，控制器不应影响矩阵A的主对角线，因此可以选择：

(6)

式中：fi是状态变量x的第i个元素；xj(i≠j)是状态变量x的第j个元素。显然，这不会影响A的主对角线。接下来，设:

fi(σxj,ε)=εsin(σxj)i,j=1,2,…,ni≠j

(7)

式中：ε、σ为可以调整的控制器参数。

容易证明式(3)的所有解都是全局有界的[18]，区间如下所示：

(8)

式中：ε、σ是常数;x(0)是初始值。

(9)

式中：e=0,±1,…。

由式(9)，本文定义如下行列式：

(10)

k=1,2,…,n

(11)

k=1,2,…,n

由式(11)可以得到：

(12)

其中K为斜率，其计算如下：

(13)

(14)

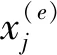
(15)

然后，令斜率|K|≪1。假设所有的平衡分布非常接近水平轴，所以cos(σxj)≈±1(e=0,±1,…,±E/2)。

因此，式(3)的系统只包含两种鞍焦点平衡，相应的雅可比矩阵如下：

(16)

详细设计标准如下：

(1) 全局有界设计准则。使标称系统Cx为渐近稳定的线性系统，式(6)所示的非线性反馈控制器一致有界。然后，式(2)的n维控制系统是全局有界且满足式(8)区间。

(2) Lyapunov指数设计准则。设计控制系统(式(2))满足以下条件：对于n维连续系统，所有平衡点对应的特征值至少具有r=n-2个正实部和r=n-2个不同的发散方向。因此，式(2)的n维控制系统具有L=n-2个正Lyapunov指数。

具体的设计步骤如下：

1) 对于任意一个连续系统(式(1))，设计一个合适的控制器Bx，该控制器可以将标称系统Ax+Bx配置为以原点为稳定焦点的渐近稳定线性系统。需要保证λ1,λ2,…,λn的实部为负，使其稳定焦点为原点，由式(4)得到了一个方程组如式(17)所示。

(17)

其中λ1,λ2,…,λn可以任意给定，只需要保证其实部均为负，所以这个方程组只有b1,b2,…,bn为未知数，所以该方程组一定有解。

2) 设计合适的控制器式(6)、式(7)，上述控制系统可通过调节参数ε和σ有效控制。具体地说，对于式(16)所示的雅可比矩阵，特征值的正实部的个数是确定的。同样地，由式(4)可以得到：

(18)

(19)

同样，λ′1,λ′2,…,λ′n和λ″1,λ″2,…λ″n为任意给定的值，根据Lyapunov指数设计准则，本文只需要保证其实部为r1=n-1和r2=n-2。这两个方程组的未知数都只有b1,b2,…,bn和εσ，共n+1个，所以式(18)、式(19)也一定有解。

3) 联立式(17)、式(18)、式(19)三个方程组，有3n个方程，只有n+1个未知数，理论上解有无数组。求解这三组方程，就能得到线性反馈控制器Bx以及非线性反馈控制器f(σx,ε)。

4) 对于得到的系统，如果系统的简并度d>0，返回步骤3)，得到另一组解。当d=0时，整个循环停止。最后，正Lyapunov指数的数目达到最大值L=n-2。

2 有两个正Lyapunov指数的四维混沌系统

给定一个四维连续系统：

其中，假定系统矩阵为:

设非线性反馈控制器为:

由式(3)，可以得到：

由具体设计步骤1)-步骤2)，能得到三组方程如下：

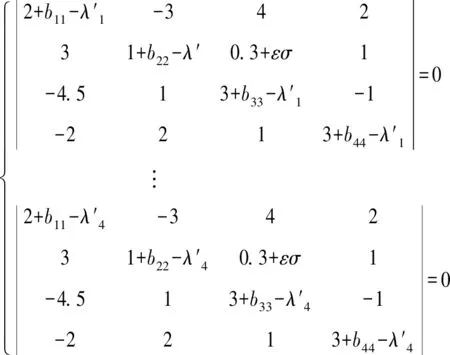
由具体设计步骤3)，得到一组解εσ=225，

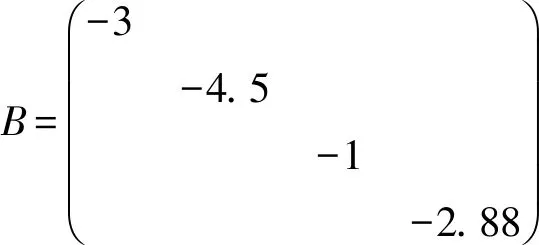
由于在求解方程之前，所有矩阵特征值已被设置为满足设计准则，令ε=15和σ=15，则受控矩阵的正Lyapunov指数的个数是L=min{r1,r2}=2，也就是说，该混沌系统具有两个正Lyapunov指数，该系统是一个无退化混沌系统，如图1所示。

图1 四维无退化混沌系统的Lyapunov指数谱

3 混沌系统量化与性能分析

3.1 混沌序列的生成

为了生存混沌序列密码，必须将混沌系统的输出x(t)转换为二进制的序列S(t)。因此引入不可逆函数Tn(x(t))，转换函数Tn(x(t))的定义如下：

(20)

3.2 混沌序列性能分析

3.2.1游程测试

游程是指序列中连续不间断的同一比特所构成的子序列。游程测试的目的是计算待测序列中游程的个数，判断“0”或“1”的游程个数是否与随机序列相近似。若以20 000比特长度的序列进行游程测试，如果各个游程长度所对应的子序列个数与满足相应的范围要求，则可以认为通过测试。表1为游程测试的范围要求和结果对比。

表1 游程测试

3.2.2相关性检验

相关性包括序列自相关性和互相关性。

序列的均值为：

(21)

式中：S(t)为系统输出的二值序列。

设S′、S″为两个混沌二值序列，k为整数。如果自相关函数r(k)满足：r(k)=0(k≠0)；互相关函数p(k)满足：p(k)→0，则序列通过检验。γ(k)、p(k)计算如下：

(22)

(23)

序列的相关性函数如图2所示。

图2 方案一相关性函数

3.2.3初值敏感性测试

对初值微小改变后，序列变化率能反映序列的产生对初值的敏感性。理想情况下，序列变化率应为50%。本文在原初值的基础上增加10-10，仿真得到变化率为49.97%，由此可知，序列的产生有很强的初值敏感性。

4 结 语

本文提出了一种基于改变矩阵特征值配置具有多个正Lyapunov指数连续混沌系统的构造方法。通过引入两个反馈控制器，配置任意受控系统轨道全局稳定，并且将正Lyapunov指数的个数配置为最大。通过本文方法，将配置正Lyapunov指数的问题转化为求解方程组。如果受控系统任意给定，按照本文方法能够很好地配置正Lyapunov指数。之后对无退化混沌系统进行量化，经过性能分析，量化后的序列能很好地应用在序列密码之中。