基于贝叶斯后验概率和非合作博弈的推荐算法

索 岩 程向羽(河南师范大学新联学院 河南 新乡 453000)

2(河南师范大学计算机与信息工程学院 河南 新乡 453000)

0 引 言

随着移动互联网的快速发展，人与人之间的社交日益网络化、虚拟化，人们越来越习惯于通过社交软件获得情投意合的朋友和感兴趣的活动。但面对庞大的社交数据，人们难以从错综复杂信息中获得自己感兴趣的内容。个性化推荐可以有的放矢地为用户推荐感兴趣的社友或活动，目前国内外学者通过不同的手段深入分析客户行为模式和交互数据以求获得用户潜在的兴趣点。例如，文献[1]利用加权平均聚合法推导用户兴趣偏好，然后融合矩阵分解和协同过滤向用户推荐好友；文献[2]利用用户好友评价矩阵分析好友的重要程度及兴趣匹配度,借助加权平均评分模式向用户推荐兴趣相似度高的好友；文献[3]利用随机游走预测单一用户兴趣偏好，聚合用户组兴趣偏好得到共同的兴趣类，为用户推荐活动或兴趣相投的好友；文献[4]利用用户好友对活动的兴趣的不同反馈，建立基于纳什均衡的好友推荐机制；文献[5]利用LDA计算用户兴趣相似度，融合用户影响力和兴趣相似度预测用户好友组整体偏好，以此向组内用户推荐书籍；文献[6]提出了一种贝叶斯地理生成模式，以签到地为组聚合组内用户兴趣，基于此向同一地理组内的用户推荐活动；文献[7]对用户的显式和隐式行为进行建模，现实用户个性化活动推荐；文献[8]研究了用户短期行为和长期兴趣偏好的关系，利用马尔可夫链解决数据稀疏问题，借助概率模型向用户个性化推荐活动。以上研究方法大多通过分析用户交互信息获取用户的兴趣偏好，以兴趣偏好为依据，采用协同过滤等方法向用户进行个性化推荐，这些方法虽然便捷有效，但受制于交互信息量少等数据稀疏问题[9-10]，推荐的查准率有待提高。为了进一步提高协同过滤推荐算法的推荐精度，本文提出了一种基于贝叶斯后验概率和非合作博弈的推荐算法。

1 用户隐式行为特性

在用户实际网络环境中，与其产生交互的无非有人或物两大类。人与人之间产生信任，人对物产生兴趣，无论是信任还是兴趣都是用户隐式行为特征。一个用户多次浏览、咨询一个活动，这些交互信息体现了用户对活动的兴趣度，表明用户可能想参与活动，同理，用户间也存在信任。这些隐式特征的背后蕴含着用户的行为趋向，本文重点考虑用户对活动的兴趣度和用户间的信任度，通过文件主题模型求取用户与其参加过的所有社交活动的主题分布，利用隐含主题概率分布来表征用户对活动的兴趣度；利用用户间的信任传递机制求取用户的直接信任值和间接信任值。假设用户集合为U，被评价过的社交活动集合为S，未被评价的新社交活动集合为S′。

1.1 用户对活动兴趣度

本文利用文件主题模型(Latent dirichlet allocation,LDA)求取用户ui参加过的社交活动S的主题分布，并用其表示目标用户ui的兴趣度。LDA假设在一个文档中包含一些主题构成的概率分布，而主题又是由一些单词构成的概率分布。设docui表示用户ui所参加过社交活动形成的文件，利用LDA求取docui中隐含主题多项式分布。参考文献[11]方法，将用户社交文件docui的主题概率分布近似看作用户对社交活动的兴趣度。在docui中隐含主题词与单词的概率wt服从超参数α的狄利克雷分布，文件与单词的概率φdocui服从超参数β的狄利克雷分布。对文件docui中的第m个单词，利用参数φdocui的多项式分布Mult(φdocui)形成单词主题配对pdocui,m，利用参数wt的多项式分布Mult(wt)对文件docui中的第m单词生成wdocui,m。据此，可得出如下生成概率：

P(W,Z|κ,γ)=P(W|Z,γ)·P(Z|κ)

(1)

式中：P(W|Z,γ)表示文档docui对应的主题概率；P(Z|κ)表示给定某个主题词生成词的概率；W、Z表示所有词集合和主题集合。由于不可能从模型中推断出参数κ和γ，采用吉布斯采样从单词可观条件下计算所属主题的概率分布P(Z|W,γ)：

(2)

(3)

(4)

(5)

设用户ui的文件为docui，社交活动sj的文件为docsj，两者所对应的主题分布为φdocui和φdocsj，为了求取用户与社交活动主题的相似度，本文引入库尔贝克-莱布勒(Kullback-Leibler,KL)散度[11]和延森-香农(Jen-sen-Shannon)散度[12]来计算两者之间的相似度，延森-香农散度定义为：

(6)

式中：KL(·)表示库尔贝克-莱布勒散度，定义如下：

(7)

JS(ui‖sj)会随着φdocui和φdocsj两者主题分布的差别而增大，这里定义用户ui对社交活动sj的兴趣度为ini,j：

ini,j=1-JS(ui‖sj)

(8)

1.2 用户间信任度

在网络社交活动中，用户间的信任一般分为直接信任和间接信任[13]。直接信任就是基于用户间的某种认知而产生的一对一信任，而间接信任就是用户因某个中间人的推荐而对另一个用户的信任。

对于给定的社交活动网络，可将其对应看成一个用户间因信任值而形成的信任网络Q=(U,E,D)，其中U表示社交用户集合，E为信任网络中有向边的集合，每一条边e(ui,uj)表示用户ui对用户uj的信任关系，D表示有向边上的信任度集合，wi,j表示用户ui对用户uj的直接信任度值。

在给定的信任网络Q=(U,E,D)中，目标用户ui对非直接信任用户ux的信任感知是基于一条可达路径pa=(ui,…,uy,uz,…,ux)，并且路径pa上任意边e(uy,uz)的信任度都大于所设定的信任阈值wθ，那么路径pa就是一条信任路径。但信任也会随着路径的加大而衰减，因此须在信任路径中规定一定的跳数阈值hθ。

若一个用户被较多的其他用户所信任，那么一般表明此用户的可信度较高，反之亦然。基于此，借鉴Pagerank算法思想求取用户的信任度：

(9)

式中：Tui表示用户ui信任用户集合；|Tui|表示信任用户集合中用户的数量；Nuj、Nur分别表示用户uj、ur被信任的用户个数。用户节点间的信任度是基于用户面对面的直接信任产生的，但在实际的社交网络中，许多用户间可能不存在或存在不明显的潜在信任关系，这样得到的信任矩阵非常稀疏，计算信任相似度的难度就会增大。为此，本文在计算用户信任矩阵前，引入信任传递以计算无交集用户间的信任度，若两个用户间没有直接信任关系，其信任度的计算式为：

(10)

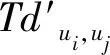
(11)

则用户之间的信任度可表示为：

式中：utumun表示用户um对用户un的信任度。

2 基于贝叶斯后验概率的行为预测

(12)

根据贝叶斯后验相关理论，可推导出用户ui参与活动sj的概率为：

(13)

式中：Sig(·)表示逻辑函数。社交活动sj对用户ui选择参与其他类似活动的贡献率πj,i计算如下：

(14)

(15)

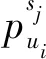
[Sig(-πj,iini,j-utumun)]δ(ci,j,1)[1-Sig(-πj,iini,j-utumun)][1-δ(ci,j,1)]

(16)

式中：δ(x,y)为克罗内克函数。根据兴趣度ini,j、用户间的信任度utuiuj过程变量的先验分布，式(16)可表示为：

(17)

这是通过贝叶斯后验概率来拟合训练样本数据以预测用户决策行为。这种行为的不确定性符合香农信息熵的概念，即一个人的行为决策是不确定的，是否决定参与受多方面信息的影响，综合正向信息越多，其参与的可能性就越大。为了使样本预测值与实际值的差值最小化，需要基于信息熵构建二者之间的对数损失函数：

(18)

建立损失函数式(18)作为优化目标：

(19)

将式(17)代入式(18)中可得：

(20)

根据高斯分布，式(20)可近似为：

(21)

将式(16)代入式(21)中可得：

Li,j∝-δ(ci,j,1)log[Sig(-πj,iini,j-utumun)]-

[1-δ(ci,j,1)]log[1-Sig(-πj,iini,j-utumun)]-

(22)

(23)

(24)

(25)

(26)

(27)

(28)

迭代终止后，算法就得到基于贝叶斯后验概率的用户兴趣和信任显示反馈：

INi,j=[in1,1,in1,2,…,ini,j-1,ini,j]i∈[1,|U|],j∈[1,M]

(29)

UTm,n=[ut1,1,ut1,2,…,ut(|U|,|U|)]

(30)

若经g轮迭代不满足以上收敛条件，则需执行第g+1轮迭代：

(31)

(32)

3 基于博弈论的活动推荐

(33)

(34)

式中：τ≥1，以保证代价函数为凸函数；ξ1、ξ2为均衡系数，并且ξ1、ξ2≥0,ξ1+ξ2=1。用户ui的效益函数为：

(35)

在其他用户不改变自己策略的前提下，用户此时所选的策略能使其他用户的策略取得最大效益，则称此时的策略组合达到纳什均衡，即：

(36)

(37)

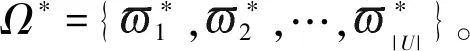
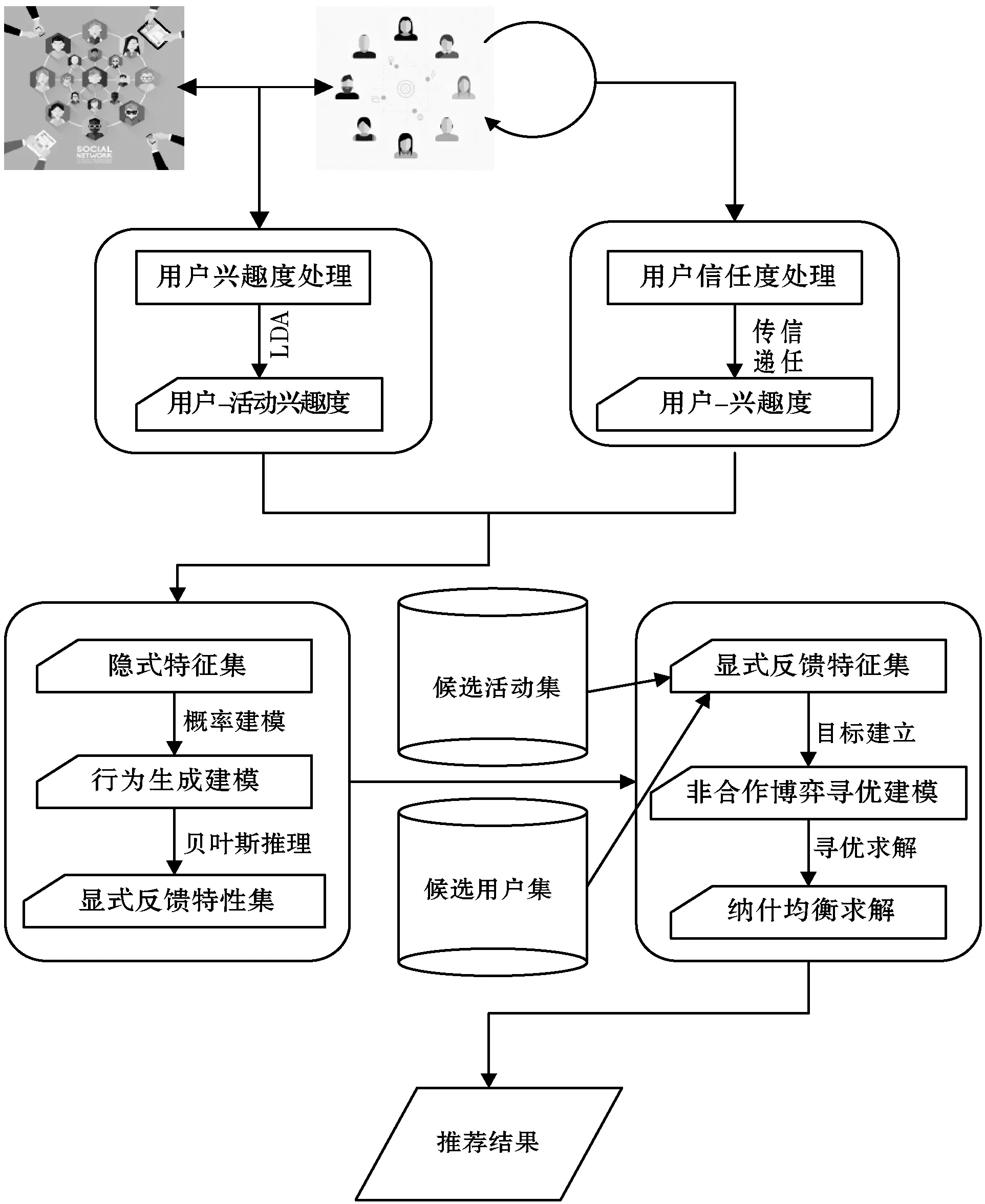
图1 算法框架示意图

4 实 验

4.1 实验数据及评价标准

为了仿真实验的有效性，这里利用豆瓣同城(北京、上海、广州、深圳)在2017年1月1日—2019年10月31日期间的所有社交活动，主要采集的信息包括用户信息和社交活动信息，具体如表1所示。

表1 数据统计明细

采用查准率Precision、查全率Recall和平均绝对误差MAE三个评价指标评估各推荐算法的性能，其计算公式见式(38)-式(40)。

(38)

(39)

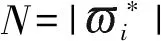
(40)

式中：Pj为候选社交活动sj的被关注数;Hj为候选社交活动sj的实际参与数；Nh为候选社交活动个数。

4.2 参数设置

(a) 参数变化对模型的影响

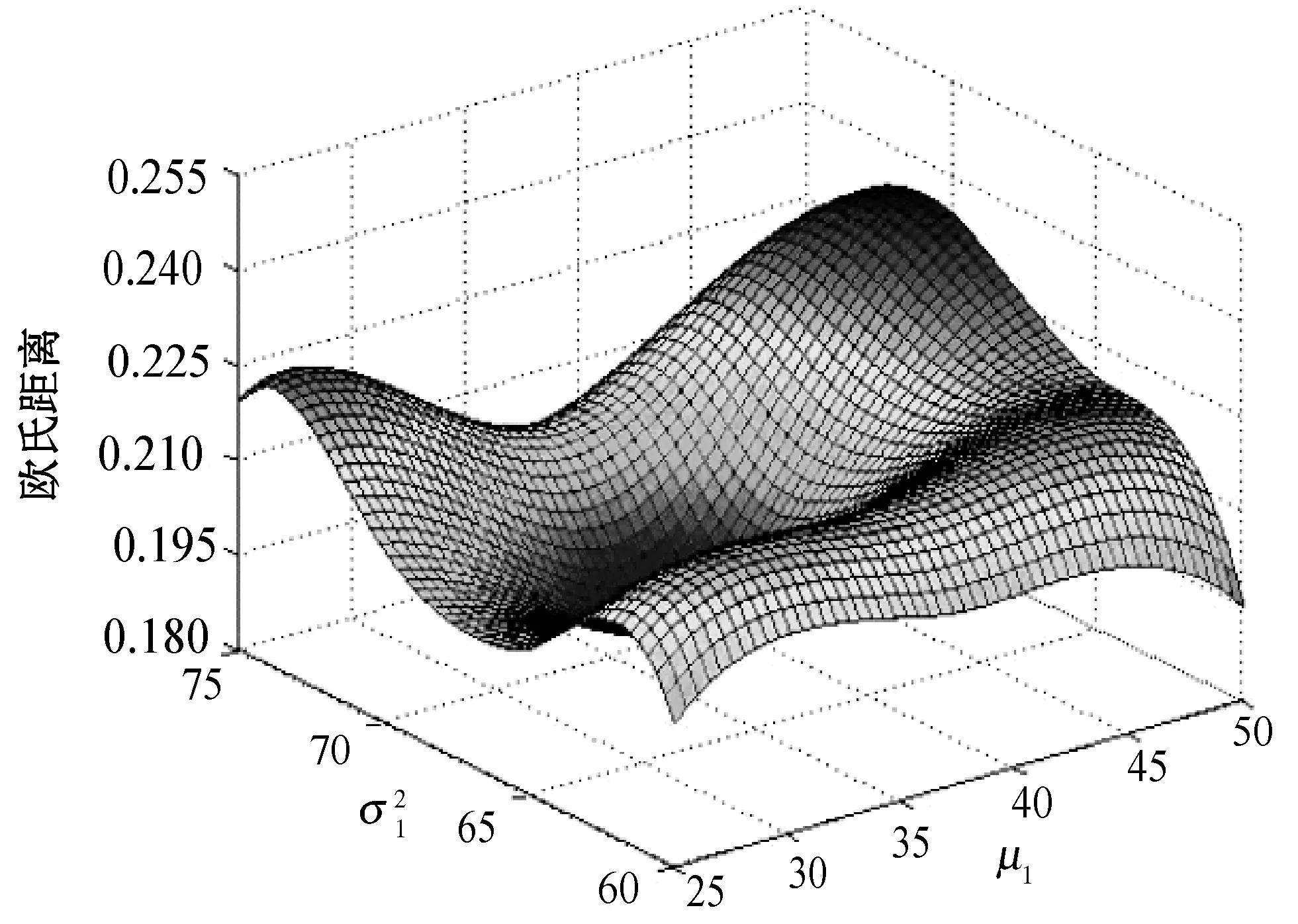
(a) 参数变化对模型的影响

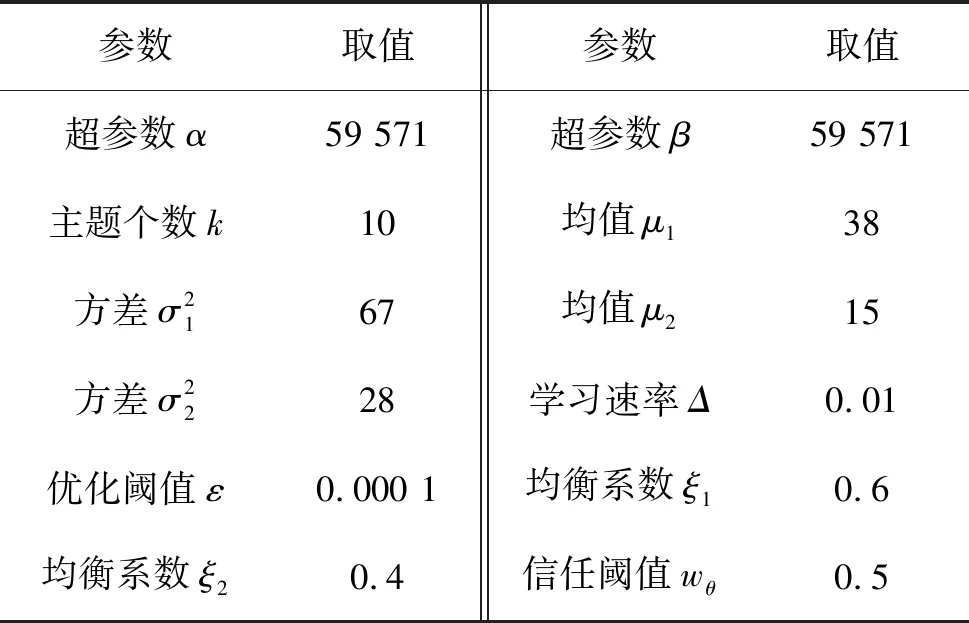
表2 参数设置

实验硬件环境为Intel(R)Core(TM) i7- 9700@3 GHz,RAM:8 GB，在Windows 7操作系统上使用Python编程实现。将豆瓣北京、上海、广州、深圳四个城市数据集合中已结束社交活动作为训练集，新社交活动作为测试集，为验证本文所提算法的性能，将本文算法与文献[14]、文献[15]和文献[16]算法进行社交活动推荐效果对比。文献[14]提出了一种基于用户行为特征的个性化推荐算法，通过学习用户以往行为特征建立潜在空间的偏好特征映射，将用户-项目交互分解为因数，并在推荐中将用户的静态和动态偏好组合在一起；文献[15]算法是一种个性化社会推荐算法，是对面向隐式反馈贝叶斯个性化排序推荐的改进；文献[16]建立用户活动交互频数的置信度，并将偏好置信度视为显示反馈的评分，借助矩阵分解策略为用户提供推荐。

4.3 不同算法的查准率和查全率对比

将四种算法分别在豆瓣同城北京、上海、广州、深圳四个数据子集上进行新社交活动推荐，N表示推荐活动的个数。不同N值下四种算法的查准率和查全率如图4所示。

图4 各算法不同N值下评价指标对比

本文算法在不同N值下的推荐指标明显优于其他三种推荐算法，说明本文算法利用贝叶斯后验概率对用户兴趣度和信任度的预测与实际情况基本一致，基于非合作博弈用户效益最大化的纳什均衡结果符合用户的实际需求，最终取得了较高的查准率和查全率。图4(a)和图4(b)展示了四种算法在豆瓣同城北京数据集上的推荐结果，随着N值的增大，查准率先增后降，查全率则是一直增大，其中在N=7之前，文献[14]算法的查准率高于本文算法。图4(c)和图4(d)展示了四种算法在豆瓣同城上海数据集上的推荐结果，随着N值的增大，查准率也是先增后降，查全率则是一直增大，只是在N=6之前，文献[14]算法的查准率高于本文算法。图4(e)和图4(f)展示了四种算法在豆瓣同城广州数据集上的推荐结果，随着N值的增大，查准率和查全率的变化趋势跟之前一样，在N=6之前，文献[14]算法的查准率高于本文算法。图4(g)和图4(h)展示了四种算法在豆瓣同城深圳数据集上的推荐结果，随着N值的增大，查准率和查全率的变化趋势跟与在北京、上海、广州数据集上一致，不同的是在N=5之前，文献[14]算法的查准率高于本文算法。综上可知，本文算法适合应用于较大规模的数据集上，随着数据集的增大，基于贝叶斯后验概率拟合的隐式特征更能符合用户的真实情况。总体上，本文算法相较于其他三种算法在查准率上至少提高了3.13%，在查全率上至少提高了2.62%。

4.4 不同算法的MAE对比

为了比较本文算法与其他两种算法在MAE上的差异，以训练集所占比例为变量，四种算法MAE的变化如图5所示。

图5 不同算法间的MAE对比

可以看出，四种算法随着训练集所占比例的增加，MAE都呈下降的趋势，但本文算法的MAE值整体上都高于其他三种算法。在豆瓣同城北京和上海数据集上，当训练集所占比例大于70%后，本文算法的MAE值明显高于其他三种算法，且MAE下降的幅度缓慢；在豆瓣同城广州和深圳数据集上，本文算法的MAE值在各个比例训练集省都高于其他三种算法，但整体上小于豆瓣同城北京和上海数据集上的MAE值，这是由于后两个数据集的规模和新社交活动量都小于前两个数据集，这对贝叶斯后验概率的拟合造成偏差，最终导致活动推荐结果与实际值的偏差变大。

5 结 语

针对传统协同过滤推荐算法推荐精度低等问题，提出了一种基于贝叶斯后验概率预测和非合作博弈的个性化推荐算法。算法将用户的兴趣度和信任度等隐

式特征赋予合理的先验分布，建立隐式特征生成过程的联合概率表达，借助贝叶斯后验概率预测隐式特征后的显式反馈；将推荐结果转化为非合作博弈中用户效益最大化的纳什均衡求解，最终活动推荐给用户的活动集合。与其他三种推荐算法相比，本文算法有较高的查准率、查全率和平均绝对误差。但先验模型参数的获取仅靠经验，如何进一步降低参数的敏感性将是后续研究的重点。