图像多尺度几何分析域隐马尔可夫树模型研究进展

王相海，宋若曦，曲思洁，穆振华，宋传鸣

（1.辽宁师范大学地理科学学院，辽宁大连 116029；2.辽宁师范大学计算机科学与信息技术学院，辽宁大连 116081；3.辽宁师范大学数学学院，辽宁大连 116029）

1 引言

近年来在调和分析理论基础上发展起来的多尺度几何分析（MGA）为图像和信号的稀疏表示提供了有效的工具支撑［1，2］.多尺度几何分析也称后小波分析，它包含了计算调和分析和稀疏逼近的发展趋势.多尺度几何分析可以看作图像稀疏分解发展的一个分支，其目的是检测、表示、处理某些高维度空间数据［1］.Wavelet变换作为一种时频分析工具，实现了对一维信号“点奇异”特性的有效表示，但其对图像及高维信号中的“线、面奇异”特性却难以实现最优的非线性逼近.后小波时代出现的具有方向性的MGA方法［3～10］，诸如Ridgelet 变换［5］、Bandelet 变换［6］、Curvelet 变换［7］、Shearlet 变换［8］、Contourlet 变换［9］和Directionlet 变换［10］等为更好地捕捉图像中的多方向边缘和纹理等信息提供了更加有效的逼近方案，从而实现了对包含高维奇异特性图像的有效稀疏表示.图像经MGA 变换后的子带具有方向性、局部性和多尺度特性，这些特性为图像压缩、去噪、融合和边缘检测等实际应用奠定了基础.近年来研究人员除了关注这些特性外，对图像分解后系数的统计规律以及子带间系数的相关性进行了积极研究，获得了图像更深层次的一些内在特性，在很大程度上提高了图像处理的效果.

作为经典的统计模型，隐马尔可夫模型（Hidden Markov Model，HMM）可对含有隐变量参数的马尔可夫过程进行描述，从可观察的参数中确定该过程的隐含参数，然后利用这些参数为后续应用作进一步的分析.在实际应用中，HMM 有多种表现形式，其概率图表现形式被称为隐马尔可夫树模型（HMT）［11］.MGA 域图像隐马尔可夫树模型通过一种树形结构建立起多尺度变换系数的隐状态与其孩子之间的关系，间接刻画了尺度间系数的相关性，更深层次地挖掘了图像的多尺度和多方向特性.图像MGA 域HMT 模型最早由Crouse等人［11］应用于Wavelet域，提出了Wavelet HMT模型，并应用于图像去噪以及纹理检索中.在此之后，学者们根据不同MGA 变换系数的统计规律特性，以及不同传递关系提出了不同形态的MGA 域HMT 模型［12～17］，并将其应用于诸如图像去噪、图像融合、纹理检索及图像分割等多个图像处理领域［18～27］.这些模型进一步揭示了MGA 变换系数之间的关系，更加有效地挖掘了图像MGA域的深度特性，提高了图像处理效果.

本文对MGA 域图像HMT模型（记为MGA-HMT）进行综述.首先，对传统MGA-HMT 模型的发展情况进行总结，并给出了模型构建一般过程的形式化描述；然后对传统MAG-HMT涉及的一些关键问题进行分析，并以此为脉络对目前MGA-HMT 模型中这些问题的解决方案和模型的发展状况进行分析和讨论；最后对MGAHMT模型未来的发展进行了展望.

2 传统MGA-HMT模型分析

传统MGA 域统计模型更多关注MGA 变换各子带内系数的关系［28～31］，难以准确刻画不同尺度间系数的相关性.Crouse等人［11］将HMT模型引入图像Wavelet变换尺度间系数中，应用“二状态、零均值”的混合Gaussian 分布对Wavelet 系数进行描述，并依据Wavelet 系数的父子传递关系建立了Wavelet-HMT模型，通过一种树形结构建立起系数的隐状态与其孩子之间的关系，开启了图像MGA-HMT这一新的研究领域.

2.1 MGA-HMT模型基本架构—以Wavelet为例

（1）图像Wavelet变换统计特性

图像经传统Wavelet 变换，可分解为一个低频子带和沿水平、竖直及对角线方向的三个高频子带.统计研究表明，图像Wavelet 变换各高频子带系数具有“高尖峰、长拖尾”的分布统计特性（如表1 所示，给出了三幅图像经3 层“db1”Wavelet 变换后第三层三个方向系数的直方图统计结果）；Wavelet 可实现对图像的的稀疏表示，即绝大多数的系数值都在零点附近，只有少量的系数幅值较大，从而可用少量非零系数来表示图像.

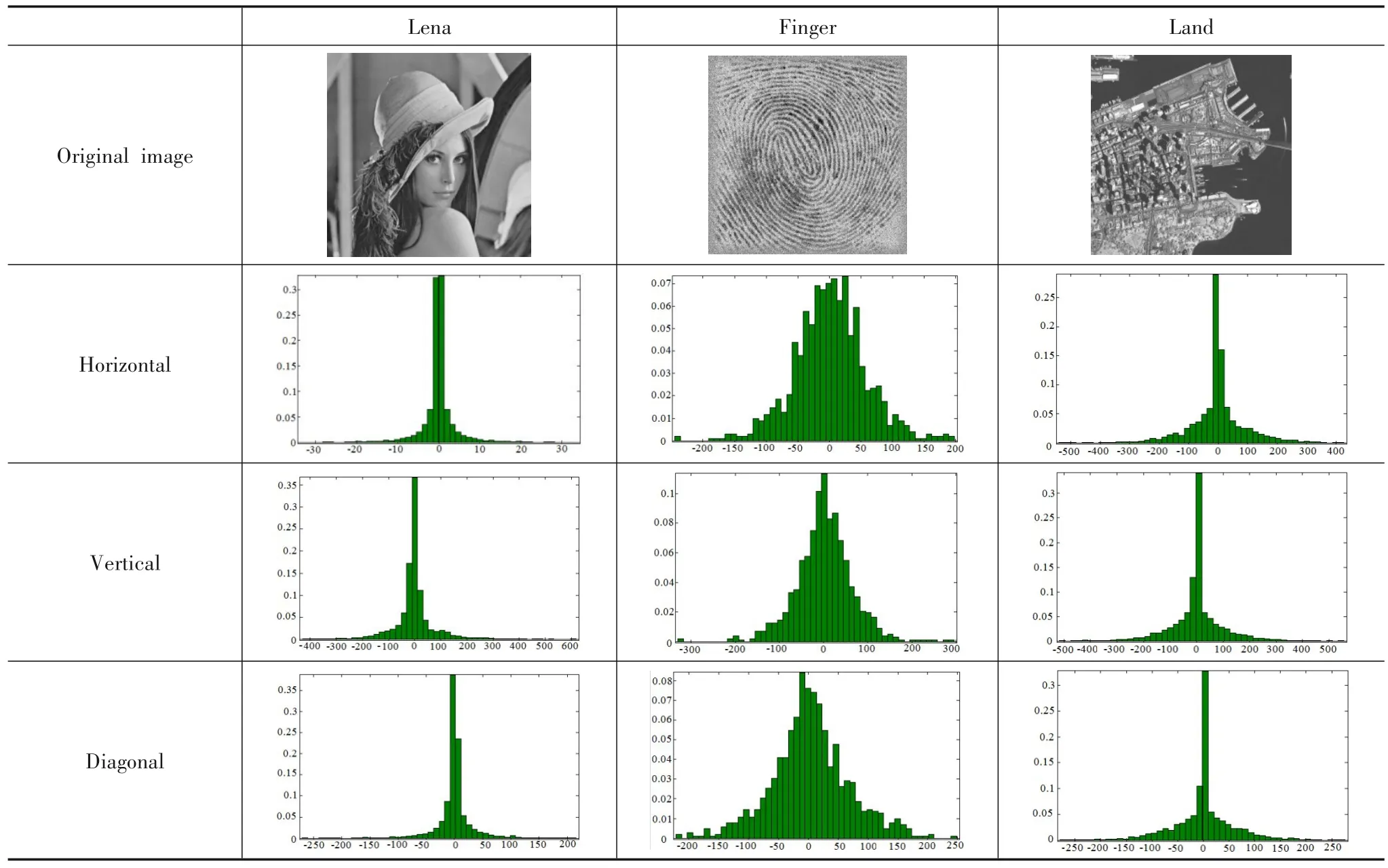
表1 图像Wavelet方向子带直方图统计

由图1 的统计结果也可以看出，Wavelet 变换各子带系数概率分布的均值为0，但其峰度值均大于Gaussian 分布的峰度值3，因此单高斯分布对子带系数的刻画能力有限［32］.为此，研究人员用高斯尺度混合（Gaussian Scale Mixtures，GSM）模型中的“大”状态和“小”状态分别对其进行建模［33］，即对数量相对较少的图像边缘区域附近的具有阶跃性变化的灰度值用GSM模型中的“大”状态建模，而对数量相对较少的图像边缘以外的区域或平滑区域的灰度值用GSM 模型中的“小”状态进行建模.如此便可以用一个方差较大及一个方差较小的Gaussian 分布和所形成的Gaussian 混合分布对小波系数进行建模.

（2）Wavelet-HMT模型的架构

对图像 Wavelet 变换方向子带系数X={x1,x2,…,xN}，进行GSM建模，即

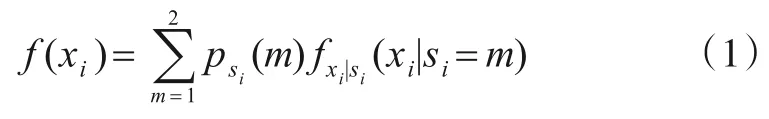
其中，si表示系数所处状态(m)表示系数分别取“大”“小”状态的初始状态概率分布，且满足表示处于不同状态时对应的Gaussian 概率密度分布函数，其表达式为

其中，μi,m和分别为Gaussian 分布待估计均值和方差.

进一步，将该GMM 作为HMT 模型的条件概率，将其中的大、小状态作为马尔可夫传递隐状态，将如图1所示的四叉树传递结构作为HMT 模型传递方式（图1中白色圆圈代表小波系数，黑色圆圈代表当前系数所对应的隐状态），构建HMT 模型（记为WHMT），并通过EM算法［34］对参数行估计.WHMT模型的参数Θ为

其中，(m)表示每棵树根节点的状态概率，m表示隐状态的个数，这里m=2；=f(si=m|sp(i)=n)为状态转移概率矩阵，代表父系数ρ(i)的状态为m的情况下其孩子系数为n的概率；表示小波各子带多元混合高斯分布大、小状态的方差.

2.2 后小波时代MGA-HMT模型发展分析

在Wavelet 域HMT 的基础上，人们对后小波时代MGA 下的HMT 进行了关注.与Wavelet 域HMT模型类似，传统经典的MGA-HMT 按照如下思路来构建模型：依据图像MGA 变换域子带的特性，对变换域系数的广义邻域关系进行定义并确定系数的传播途径，在此基础上建立相应HMT 模型，并对模型参数进行估计.该类HMT 模型的发展情况介绍如下.

2006 年Duncan 等人在文献［35］中对图像Contourlet 分解后高频子带系数进行了研究，发现Contourlet 系数具有与图像Wavelet 系数相类似的性质，即不同尺度间的系数具有一定的持续性，相同尺度、不同方向间的系数具有一定的聚集性，据此提出了一种基于Contourlet 域的HMT 模型（Contourlet-domain Hidden Markov Tree model，CHMT），并将其应用于图像去噪和检索领域.CHMT 模型与WHMT 模型之间存在较大差异.首先，与Wavelet 变换相比，图像Contourlet 变换可以定义具有方向的子带；同时，在Contourlet 变换中，每个方向子带可与多个更高频率的方向子带进行关联，从而使系数之间的传递关系更加复杂.图2（a）及图2（b）分别刻画了Contourlet系数之间的传递关系和CHMT 模型的树型结构.如图2（a）所示，Contourlet 系数通过尺度间二叉树结构进行关联，进而通过隐状态建立CHMT 树形结构.非下采样Contourlet 变换（NonSubsampled Contourlet Transform，NSCT），通过合并二维非下采样金字塔滤波器组和非下采样方向滤波器组实现图像的变换，除有效保持Contourlet 变换的多方向性和各向异性特性外，还具有平移不变特性，该特性在图像融合、去噪等应用中发挥着重要作用.文献［16］对图像NSCT 变换系数的概率统计特性进行了分析，获得了图像NSCT 变换的方向子带系数同样具有持续性和聚集性的结论，并通过一种树型结构确定了不同子带间的系数传递关系，进而构造了一种NSCT 变换的HMT 模型（NSCT-HMT），该模型在图像去噪应用中取得了比WHMT 和CHMT 更好的效果.除了Contourlet 变换的HMT 外，人们还对其他MGA 的HMT进行了研究，比如：文献［17］对拓展离散Shearlet 变换（Extended Discrete Shearlet Transform）的系数分布规律与特性进行了研究，确定了一种“父子”系数传递关系，在此基础上构建了相应的HMT 模型，并将其应用于图像去噪中；Jin 等人［14］通过对Curvelet 变换进行研究，提出了基于Curvelet 域的HMT 模型，并将其应用于SAR 图像去噪领域，取得了很好的效果；Hou 等人［15］提出了基于第二代Bandelet 变换的HMT 模型，并将其应用于图像分割中.基于上述分析，表2 对该类HMT 所采用的树形结构以及传递关系进行了梳理.

图2 CHMT模型

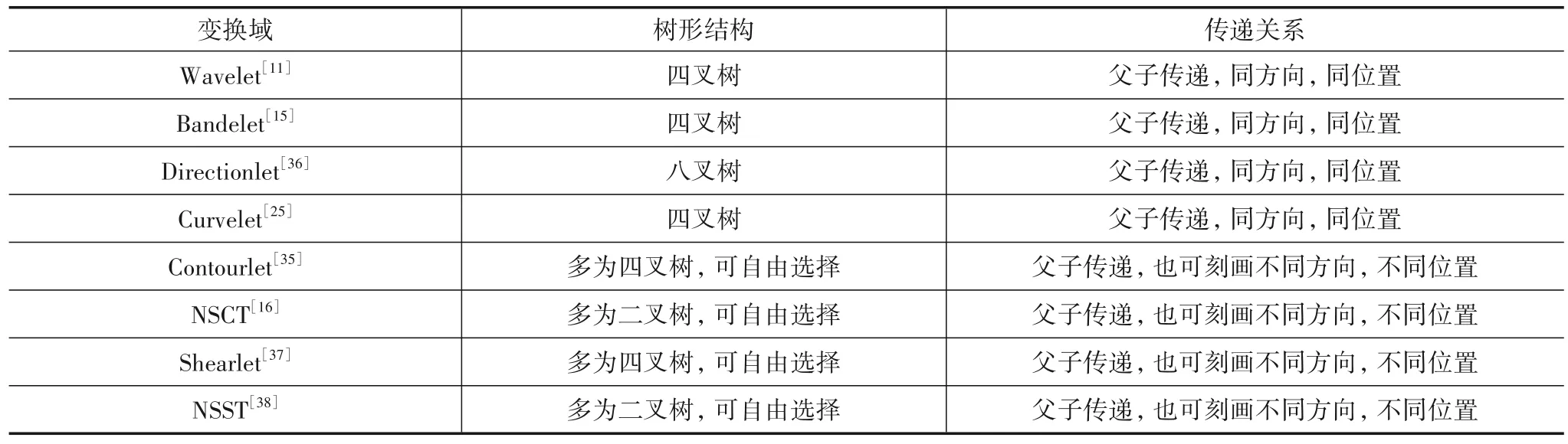
表2 经典MGA-HMT 系数传递关系

2.3 MGA-HMT模型构建的一般过程

分析现有的传统MGA-HMT模型可以发现，该类模型的构建需满足以下两个条件：一是MGA 变换域高频系数的概率分布直方图须具有“高尖峰、长拖尾”的特性；二是同一方向不同子带系数间具有一定的连续性和依赖性，这种状态变量的依赖性可以通过状态转移概率矩阵进行描述.MGA-HMT通过系数隐状态的传递规律对系数间的马尔可夫性进行刻画，其构建的一般过程可归纳如下.

（1）将图像MGA变换域内系数分为两类：一类是数量非常多的小值系数，称为“小系数”，表示图像中的平滑区域或者背景区域信息；另一类是数量较少的大值系数，称为“大系数”，表示图像中的边缘或者纹理信息.

（2）利用两个Gaussian 分布函数混合来描述MGA变换域系数，一个Gaussian 分布函数描述“大系数”，另外一个描述系数中的“小系数”，从而建立起MGA 变换域系数的GSM.

（3）建立变换域系数在相同方向、不同尺度高频子带间的树形结构，并利用状态转移概率矩阵ε来描述这种树形结构间的状态状态转移概率.

（4）进一步形成MGA-HMT模型参数集，即

其中，πm(m=1,2,…,M)为初始概率分布矩阵1,2,…,P；m,n=1,2,…,M)为状态转移概率矩阵，其含义为在已知父节点ρ(i)的隐状态变量sp(i)的值为n时子节点i的隐状态变量si的值为m的条件概率；θ={θ1,θ2,…,θr}为混合参数，满足f(coef)=(coef)（其中，f(·)表示观察值概率密度值，P(·)表示观察值概率密度分布函数，通常为混合高斯分布）.

3 MGA-HMT 模型的几个关键问题及研究进展

前面介绍的传统MGA-HMT 模型均采用了“二状态、零均值”的GSM 作为HMT 模型中刻画图像MGA 系数的条件概率密度函数，并采用子带系数间的“父子”关系作为马尔可夫链传递规律，同时应用EM 算法对模型的参数进行估计.然而研究发现，这种传统的MGAHMT模型有如下几个关键问题值得关注.

（1）GSM 并非是对所有MGA 子带系数刻画的最佳选择［39～41］，而在HMT模型的建模过程中，对各子带的概率密度分布表示至关重要.

（2）采用“父子”传递关系描述MAG 子带的传递特性仅仅刻画了MGA 子带间系数一个维度的相关性，事实上图像MGA变换的子带系数除了这种“父子”之间的相关性外，往往还会存在其他维度的相关性，如“邻域”相关性和“堂兄弟”相关性等［42，43］，有时这些相关性会表现出更强的预测能力.

（3）应用EM 算法对HMT 模型进行估计往往会存在计算复杂度大的问题［44，45］.

（4）传统MGA-HMT 为2D 模型，对诸如视频、高光谱图像等具有三维性质的多维图像的处理受到限制［46，47］.

以上这些问题直接影响到HMT 模型的预测精度、实施效率和应用范围.近年来这些问题引起了人们的关注，并且人们从不同方面提出了一些解决思路.本节以这些问题为导向，分别对其目前的研究进展进行分析和讨论.

3.1 图像MAG变换系数的概率分布问题

由于不同MGA 变换系数呈现的统计规律不同，因此其最佳概率密度分布函数也存在差异，这样GSM 拟合并非对所有情况都是最佳的选择方案.目前从发表的文献来看，有两种方案可以解决该方面的问题：一种是最适概率密度分布法，另一种是多态HMT法.

最适概率密度分布法最早由Goossens 等人在文献［39］中提出，其基本思路为寻找最适合当前MGA 变换系数的概率分布模型，对其处理后用以替代传统HMT模型中的GSM.常见应用的概率分布模型包括BKF 分布［40］、Weibull分布［41］、Cauchy 分布［48］和Laplace 分布［49］等.Goossens 等人［39］首先对图像Wavelet 变换中“感兴趣”系数和“无兴趣”系数进行定义（如图3（a）所示），通过对Wavelet 系数进行统计分析，获得了BKF 分布可对Wavelet 系数进行最好拟合的结论，并提出了一种BKF分布参数估计方法.使用GSM 方法拟合出原始图像系数大、小为“无兴趣”系数和“感兴趣”系数的条件概率密度函数，在此基础上构建新型Wavelet 域HMT 模型，其树形结构如图3（b）所示，黑色节点为小波系数，S-节点和Z-节点分别表示隐乘数和与小波系数关联的显着性.实线表示子带的父子传递关系，虚线表示空间相关性的传递关系，并通过EM 算法对模型参数进行估计.该模型与传统Wavelet-HMT 相比，更好地对Wavelet 系数进行了拟合，在很大程度上提高了W-HMT 模型的精度以及效率.

图3 Goossens HMT模型[39]

进一步，文献［40］利用几种经典的概率分布模型分别对拓展Shearlet 系数进行拟合，并应用KS（Kolmogorov Smirno）值作为客观评价指标对拟合效果进行了比较，并在文献［39］的模型架构下通过增加系数尺度间平均圆锥比率概率密度的计算，建立新型ES-HMT模型，与文献［39］相比能更好地刻画系数之间的传递关系，同时利用Shearlet 变换可以刻画更多的变换方向.然而，上述模型均采用单一概率密度分布刻画所有系数，事实上即使在同一种多尺度变换下，不同类型的图像其多尺度系数也会根据自身图像特性呈现特定的特征，这时构建一个自适应混合分布就显得尤为重要.文献［50］对NSCT 方向子带系数的概率密度分布进行了研究，提出一种基于NSCT 方向子带系数峰值自适应调整的混合Gaussian-Cauchy 分布，该分布能根据NSCT子带系数特性通过权函数自适应地调整分布的表示，具有更高的拟合精度.在此基础上结合NSCT-HMT 框架，提出一种新型NSCT-HMT 模型，利用自适应分布对多尺度变换系数进行刻画可以实现对不同图像的多尺度变换系数更灵活的表示，很大程度上提高了拟合精度.此外，Sadeghigol 等人在文献［51］中提出了最适概率密度分布法实现的另一种思路，即通过选取混合函数来代替传统HMT 模型中的GSM，并由EM 算法直接对参数进行估计.相似的研究工作在文献［52］中也有体现.

多态HMT 方法由Zhang 等人在文献［53］中提出，为了进一步提高对MGA 变换系数的刻画精度，将传统HMT模型的隐状态数量由2个扩展为3个，用“大”“中”和“小”状态分别对应图像边缘、半边缘和平滑区域，并称之为“三态”HMT模型（如图4所示），其计算公式为

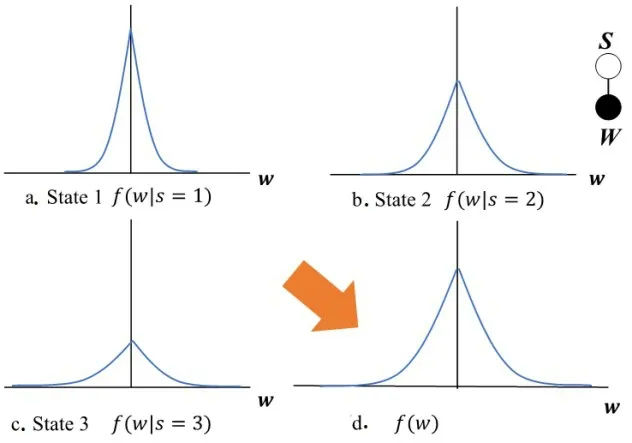
图4 三态隐Markov示意图[53]

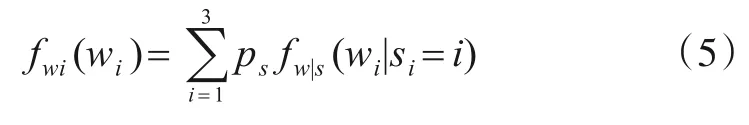
三态HMT 模型是对传统HMT 模型的改进，通过增加隐状态数目，采用三状态GSM 代替二状态GSM，能好地拟合图像MGA 系数的非高斯性，提高HMT 模型参数估计的准确性，在一定程度上提高模型参数集和真值图像MGA 变换系数的匹配程度.该三态HMT模型为多尺度域多状态HMT 模型的构建提供了思路，即通过实现对HMT 模型中状态数量的改变更加精细地刻画图像特有的统计特性，以突破传统HMT模型中仅对边缘区域和平滑区域两类系数进行描述的限制.

综上所述，传统MGA-HMT模型采用“二状态、零均值”的GSM 作为HMT 模型的概率密度分布函数，但由于不同类型图像在不同MGA变换域下会呈现出不同的统计特性，因此概率密度分布函数的选取就显得尤为重要.目前出现了两类改进模型分别从多概率分布选取和多状态拟合两个方面对传统模型进行了改进，在一定程度上提高了模型的预测精度，但总体而言这方面的工作还不是很多，特别是基于多态HMT 模型的研究.

3.2 模型的多维预测问题

传统MGA-HMT 模型使用“父子”传递关系描述MGA 变换子带的传递特性，仅仅刻画了MGA 变换尺度间子带系数的相关性，而忽视了其他子带间可能存在的一些传递特性，对这些特性进行挖掘并用以指导HMT 模型的传递关系，势必会给HMT 的精度提高带来帮助.

关于这方面的问题，文献［54］首次提出一种基于多传递关系的HMT 模型即HMT-3S 模型，并将其应用于图像分割处理中.该模型借助于图分组技术将图像二维Wavelet 变换的三个子带集结成一个树结构（如图5 所示），融合了Wavelet 三个子带间的相关性，除了像传统Wavelet-HMT模型那样对Wavelet系数尺度间的相关性进行捕捉外，还能对子带内相关性进行很好的刻画.该模型在传统Wavelet-HMT 模型的基础上在尺度间传递的概率转移矩阵中增加了3 个参数（共8 个参数），从而使模型能够更准确地描述具有相同纹理区域的小波系数间的关系.

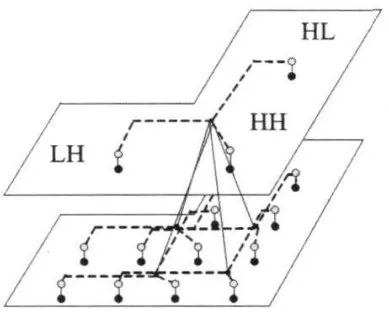
图5 HMT-3S模型[54]

然而，图像Wavelet 分解子带的方向性有限，使得HMT-3S 应用在图像分割上的分割结果区域一致性不强，分割边缘也不够清晰.文献［55］将HMT-3S 模型框架应用于SAR 图像的第二代Bandelet变换系数HMT建模中，较好地解决了Wavelet 域HMT-3S 模型的图像分割结果区域一致性较差和分割边缘不够清晰问题.此外，文献［42］也采用了该框架构建了Contourlet 域的HMT-3S模型.

文献［43］提出一种基于系数多状态关联的HMT模型（M-NSST-HMT），首先，对NSST 兄弟子带间的相关性进行统计，获得图像NSST 系数兄弟子带间具有与父子系数间类似的统计特性，同时将兄弟间的持续性与聚集性作为HMT 模型状态转移参考因素之一，其树形传递结构如图6所示，并采用互信息作为系数之间相关性的客观评价指标，建立自适应权重函数决定兄弟系数与父系数对当前系数影响的权重.M-NSST-HMT 模型被应用于图像去噪中，取得了较传统NSST-HMT更好的去噪效果，同时为进一步探索MGA-HMT模型的多状态传递关系提供了一种思路.文献［56］重新定义了NSCT方向子带系数的广义邻域关系，并对其联合概率密度分布进行了研究，获得NSCT 系数与其四邻域系数存在最强相关性的结论；然后，对NSCT 系数与其四邻域系数分别应用Gaussian Copula 建模，并根据其Copula熵值，建立基于Copula 熵的多元GSM，克服了传统HMT 模型只考虑尺度间传递关系而忽略了尺度内传递关系的问题，结合隐马尔可夫树模型架构，构建了一种基于Copula 熵多元混合高斯分布的隐马尔可夫树模型.

图6 M-NSST-HMT树形传递结构[43]

综上所述，深入挖掘图像MGA 变换系数的多维度相关性，用以指导相应HMT模型的状态传递过程，对提升模型的预测能力具有很大帮助.

3.3 参数的快速计算问题

EM 算法［34］又被称为期望最大化算法，对依赖于无法观测的隐性变量的概率模型，该算法可有效地寻找参数最大似然估计或者最大后验估计.传统MGAHMT 模型大都采用EM 算法对参数进行训练，然而该算法需要通过多次“期望-最大化”的迭代才能实现［57］，从而导致HMT 模型的训练过程具有较高的计算复杂度，这在一定程度上影响了模型的运算效率，限制了HMT 模型的实际应用.针对该类问题，文献［44］提出了一种无需模型参数训练的基于快速分类的Wavelet 域HMT 模型的参数估计方法，对每个子带的Wavelet 系数根据空间自适应阈值被分为两类，分别对应于传统HMT 模型中GSM 模型的“大状态”和“小状态”，然后利用局部统计量实现对模型参数的估计.该方法为HMT 模型的参数估计提供了一种新思路.在此基础上，文献［45］将该模型框架应用于双树复小波变换中，提出了一种非训练复小波HMT 模型，并将其应用于图像去噪中.与传统HMT 模型相比，该模型具有较高的计算效率，同时也取得了很好的去噪效果.

综上所述，在MGA-HMT 模型中，参数的训练和估计效率直接影响到模型的实际应用.尽管传统MGAHMT 模型中所采用的EM 算法可有效地保证对参数的估计精度，但其存在参数训练计算复杂度高的弱点.如何有效地提高模型参数的计算效率是一个需要关注的问题，而目前这方面的研究文献还不是很多，还有待更深入的研究.

3.4 模型的3D延拓问题

传统MGA-HMT 模型是针对2D 静态图像提出的，若直接应用于诸如视频、高光谱影像和计算机断层扫描医学图像等3D 数据，只能逐帧（波段）对图像进行处理，这将使模型的执行效果和效率受到极大的限制.目前，有文献报道了两类方法可实现对传统MGA-HMT模型的3D 延拓：一种是基于多维度预测的3D-HMT 模型构建方法，另一种是基于3D 多尺度分析的3D-HMT 模型构建方法.

对于第一种方案，文献［46］从空间维和光谱维两方面对高光谱（HyperSpectral，HS）影像NSST 高频方向子带的特性进行研究，通过对HS 波段影像NSST 高频方向子带系数的概率密度分布进行估计，获得了HS 影像NSST 系数具有“高尖峰、长拖尾”的特性；通过对HS波段影像空间维和光谱维NSST 高频方向子带系数的广义邻域相关性进行统计分析，获得了HS 影像NSST高频子带系数在空间维和光谱维均具有“聚集性”和“持续性”的特性，即空间维不同尺度、相同方向高频子带中的父子系数，以及光谱维高频子带系数与随后相邻几个波段对应系数的状态均具有一定的相关性；在此基础上提出了一种HS 影像NSST 域的隐马尔可夫森林模型（NSST-HMF）对HS 影像NSST 系数的相关性进行刻画（图7 给出了NSST-HMF 空-谱维方向子带间系数传递关系），第一次在HS 影像HMT 的预测结构上同时考虑了空间维和光谱维两种状态的相关性来协同指导HMT模型的系数预测，提高了模型的预测准确性.

图7 NSST-HMF多维度系数传递关系示意图[46]

近年来3D-MGA作为MGA领域的研究热点受到关注［4］.经典3D-MGA 工具包括Surfacelet 变换［58］、3DWavelet变换［59］和3D-Shearlet变换［60］等.文献［47］提出一种Surfacelet 域的3D-HMT 模型用于视频烟雾检测.Surfacelet 延伸了2D Contourlet 变换的思想，首先应用“沙漏型”滤波器对视频进行三个方向的滤波，再用“棋盘形”滤波器和重采样矩阵建立方向滤波器，其相应频带划分如图8（a）所示.所构建的3D-HMT 模型采用了GSM 对每个子带系数进行描述，再通过EM 算法对模型参数进行估计，结合SVM 支持向量机模型实现对烟雾视频的烟雾检测，实验结果验证了所提3D-HMT模型的有效性.

图8 Surfacelet的频带划分和八叉树结构[47]

综上所述，尽管目前关于MGA-HMT 模型3D 延拓方面的文献还不是很多，但上述两个文献为3D-HMT模型的构建和应用提供了思路.

4 总结与展望

随着MGA工具的不断发展，对其系数分布、传递规律的研究显得愈加重要.20 世纪90 年代以来，MGAHMT 模型成为图像统计模型领域的一个重要研究方向.本文以传统MGA-HMT 模型的一般架构、MGAHMT 模型所涉及的关键问题及其发展为脉络对MGAHMT模型进行了综述.首先，以Wavelet-HMT模型为例对MGA-HMT 模型的基本架构进行介绍，同时对传统MGA-HMT 模型的发展情况进行了分析；然后，对传统MGA-HMT 模型的一些关键问题进行了阐述，并对每一问题的研究进展、解决思路进行了分析和讨论.近年来尽管MGA-HMT 模型受到关注并在很多图像处理领域得到了很好的应用，然而正像本文第3 节所讨论的那样，MGA-HMT 模型中有很多关键问题的研究尚处于起始阶段，特别是随着MGA 理论和工具的不断发展，这些问题有待进行更深入的研究.本文认为未来MGA-HMT 模型研究领域在以下4 个方面的工作应该受到重视并得以发展.

（1）MGA-HMT模型有效性评价指标体系的建立

尽管MGA-HMT模型的基本理论架构已趋于完善，但对模型的有效性评价还停留在模型后续应用的有效性评价上.事实上，同一模型应用于不同领域其性能可能会产生较大的差异.MGA-HMT模型的主要功能是对图像多尺度系数之间的传递关系进行刻画，这样仅通过实际应用效果而对模型优劣进行评判势必会具有一定的片面性.直接针对MGA-HMT 模型建立评价指标体系不仅有利于MGA-HMT 模型自身的发展和对多尺度分解系数相关性的判断，而且也会为HMT 模型的实际应用提供必要的指导.

（2）MGA-HMT模型与学习方法的结合

近年来，深度学习、字典学习等基于学习的图像处理方法［61，62］展现出旺盛的生命力.HMT 模型作为经典的概率图模型，可以对图像特征的传递关系进行很好的刻画，而学习方法的实质也是对图像特征进行提取，因此如何建立合理的HMT模型并与图像的学习过程相关联是值得期待的工作.目前这方面的研究工作已初露端倪［63，64］，相信未来这方面会得到很好的发展.

（3）适应新MGA发展的HMT模型构建

MGA 为图像提供了一种具有方向性的稀疏表示方法.继Wavelet变换对图像中奇异点特性进行有效表示之后，后Wavelet时代的MGA为具有面奇异或线奇异的高维奇异特性提供了一种更优或更稀疏的表示方法，从而为更好地捕捉图像中的多方向边缘和纹理等特性提供了有效的支撑.但MGA 发展的脚步却并没有停止，比如U-系统［65］、V-系统［66］等后MGA 方法正在氤氲而生，同时也为图像的稀疏表示提供了新的支撑.挖掘这些后MGA特性，探究其系数之间的传递及依赖关系，进而建立相应的HMT 模型，对于促进这些MGA 的发展、更好地满足不同应用领域的需求具有重要意义.

（4）3D-MGA下3D-HMT模型的发展

2D-MGA、3D-MGA的研究起步较晚，目前发展尚未完备，许多问题还在探索中［4］.已出现的3D-Wavelet 变换、3D-Contourlet 变换和3D-Shearlet 变换等3D-MGA 变换［4，67，68］在对3D 图像（影像）的稀疏表示和特征刻画上拥有独特的优势.然而目前研究这些3D-MGA 系数统计规律的文献还很少，而基于3D-MGA 的3D-HMT 模型则更少.相信随着高光谱影像、核磁共振影像和计算机断层扫描影像等3D 图像（影像）处理和应用需求的快速增加，该领域的研究将会得到很好的发展.