基于噪声初始化、Adam-Nesterov方法和准双曲动量方法的对抗样本生成方法

邹军华，段晔鑫，2，任传伦，邱俊洋，周星宇，潘志松

（1.陆军工程大学指挥控制工程学院，江苏南京 210007；2.陆军军事交通学院镇江校区，江苏镇江 212003；3.华北计算技术研究所，北京 100083；4.江南计算所数字工程与先进计算国家重点实验室，江苏无锡 214083）

1 引言

深度神经网络（Deep Neural Networks，DNNs）在图像分类［1］、目标检测［2］等领域取得了巨大突破，但相关研究表明DNNs 存在着脆弱性，容易被精心设计的对抗样本［3］所攻击.进一步的研究表明，对抗样本具有迁移性［4］，即针对某个DNN 生成的对抗样本，同样可以让其他未知的DNNs 输出错误结果.对抗样本还能威胁现实应用［5］，因此大量研究致力于提高DNNs 的防御能力，如对抗训练［6］、样本去噪声［7］、样本转换［8］和其他方法［9］.综上所述，对于对抗样本迁移性的研究，有助于提高DNNs的鲁棒性，并使得现实应用更加可靠.

Foolbox［10］将对抗样本的生成方法分为3 种：基于梯度的方法［11］、基于分数的方法［12］、基于输出的方法［13］.其中基于梯度的生成方法主要依靠对抗样本的迁移性来实现对黑盒DNNs 的攻击.本文主要研究对抗样本的迁移性，具体为分类任务中基于梯度的对抗样本生成方法.现有方法可以相互组合，形成更具迁移性能的攻击.例如，现有较强的攻击组合NI-TI-DIM 由Nesterov 算法［14］、动量算法［11］、样本多样化方法［15］和平移不变方法［16］组合而成.

目前，随机噪声初始化［10］是仅有的对抗噪声初始化方法.本文提出噪声初始化方法，通过像素偏移方法来预先增强干净样本的攻击性能.同时，本文提出基于Adam-Nesterov 方法和准双曲动量方法的对抗样本生成方法，以对抗样本的迁移性能.现有的Nesterov 算法［14］可理解为标准动量在求解梯度之前添加了一个临时的校正因子，但每次迭代中的Nesterov 动量共享一个相同的学习率.而本文基于Adam-Nesterov 方法的对抗样本生成方法，可以自适应地调整学习率，且Nesterov 动量中的每个权值都有独立的学习率.此外，本文将准双曲动量算法用于对抗样本生成，取代常规动量算法［11］.以NI-TI-DIM 为例，对抗样本生成框架及本文方法所改进的位置如图1 所示.本文在梯度计算前，将噪声初始化操作作为一个模块加入其中，并用准双曲动量算法和Adam-Nesterov 方法分别取代动量方法［11］和Nesterov 算法［14］.实验表明，结合了本文方法的攻击组合能生成攻击成功率更高的对抗样本.同时，实验表明，3种方法都没有额外增加对抗样本生成所需的运行时间和运算资源.

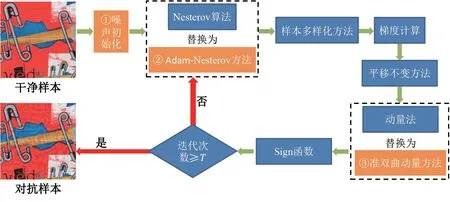
图1 本文方法框图

2 相关工作

2.1 对抗样本问题的定义

对于一个已知训练好的深度分类器f(x)：x∈X →y∈Y，向其输入干净样本x，分类器输出正确的标签y.对抗攻击是在干净样本x邻域找出一个对抗样本xadv，使得分类器输出错误的标签.对抗攻击分为无目标和有目标攻击，其中，无目标对抗样本能使得分类器的输出标签不等于正确标签，即f(xadv) ≠y，有目标对抗样本能使得分类器的输出标签等于目标错误标签ytarget，即f(xadv)=ytarget≠y.通常情况下，为了让干净样本x和对抗样本xadv难以通过人眼进行区分，攻击者会将干净样本x和对抗样本xadv之间的Lp距离限制在足够在足够小的范围ε内，即‖xadv-x‖p≤ε，其中p可以是0，1，2或者∞.本文主要关注L∞条件下的无目标攻击方法.

对抗样本具有迁移性，以无目标攻击为例，针对深度分类器f1(x)生成的对抗样本xadv，不仅可以使f1(x)输出错误的标签f1(xadv) ≠y，还可以使其他未知模型f2(x)，f3(x)，…，fn(x) 输出错误的标签f2(xadv) ≠y，f3(xadv) ≠y，…，fn(xadv) ≠y.

2.2 基于梯度的对抗样本生成方法

2.2.1 快速梯度符号方法

Goodfellow 等人提出的快速梯度符号方法（Fast Gradient Sign Method，FGSM）［3］解决了对抗样本生成速度过慢的问题.FGSM 通过最大化损失函数J(x，y)来找出相应的对抗样本：

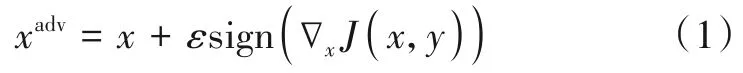
其中，∇xJ(x，y)是损失函数对于x的梯度，ε是干净样本x和对抗样本xadv的L∞距离的限制阈值.

2.2.2 多次迭代的快速梯度符号方法

Kurakin 等提出多次迭代的快速梯度符号方法（Iterative Fast Gradient Sign Method，I-FGSM）［17］，解决了FGSM 在白盒攻击中成功率过低的问题.I-FGSM 以更小的步长α，通过T次迭代的方式重复快速梯度方法，从而找出白盒攻击能力更强的对抗样本.

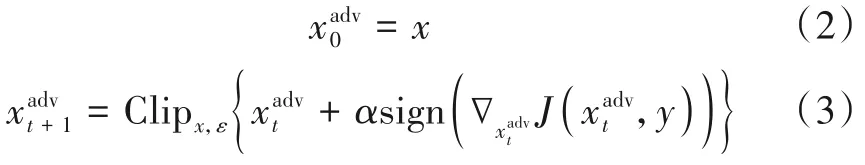
其中，α为步长.对抗样本通过Clipx，ε{·}方程满足L∞限制条件，并限制对抗样本的每一个像素点于区间[0，255]内.Clipx，ε{·}的定义为

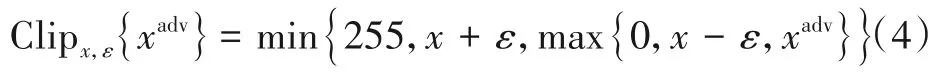
尽管I-FGSM 在白盒攻击方面性能卓越，但在黑盒攻击方面却远差于FGSM.

2.2.3 基于动量方法的多次迭代快速梯度符号方法

Dong 等提出基于动量方法的多次迭代快速梯度符号方法（Momentum Iterative Fast Gradient Sign Method，MI-FGSM）［11］，缓解I-FGSM 迁移性能过低的问题.MIFGSM 将优化算法中的动量算法应用于对抗样本生成中，其更新过程为

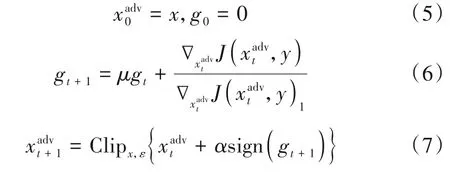
其中，gt+1为前t次迭代中累加的梯度，μ为动量系数.

2.2.4 基于Nesterov 算法的多次迭代快速梯度符号方法

Lin 等提出基于Nesterov 算法的多次迭代快速梯度符号方法（Nesterov Iterative Fast Gradient Sign Method，NI-FGSM）［14］，增强了对抗样本的迁移性能.初始化=x，g0=0后，其过程为

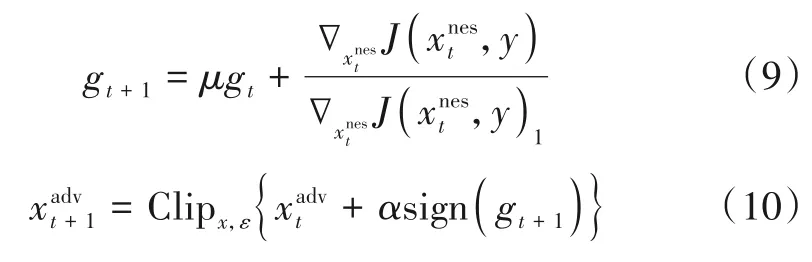
2.2.5 集成学习方法

Dong 等通过集成学习联合多个模型共同生成对抗样本［11］，其核心为融合所有K个模型的logits，并通过标签和融合的logits计算新的交叉熵损失.

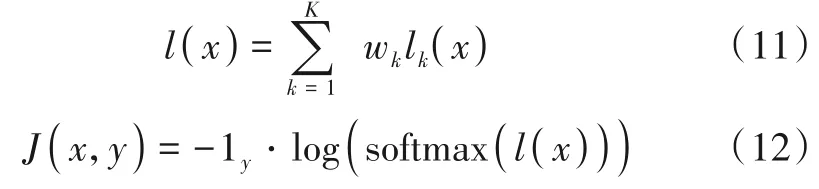
其中，l(x)表示第k个模型的logits，wk表示集成系数，-1y表示标签的独热编码.集成学习方法能大大提升对抗样本的迁移性能，但也增加了对抗样本生成的时间和资源.

2.2.6 样本多样化方法

Xie 等提出了样本多样化方法（Diverse Input Method，DIM）［15］，在每次迭代中，提前对输入样本进行随机的多样化转换.其过程为

其中，s表示多样化转换后的样本大小，p表示执行转换的概率.

2.2.7 平移不变方法

Dong 等提出了平移不变方法（Translation-Invariant Method，TIM）［16］，在每次迭代中，通过集成多个平移单个像素的样本来提升对抗样本迁移性能.同时，为了解决效率问题，Dong 等将这种样本的集成等价为对梯度信息的高斯模糊.梯度信息的高斯模糊过程为

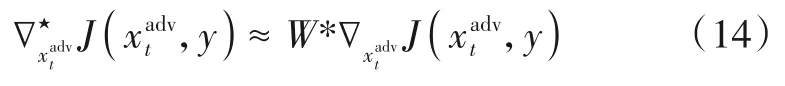
其中，W为一个预定义的高斯核.

2.2.8 尺度不变方法

Lin 等提出尺度不变方法（Scale-Invariant Method，SIM）［14］，这种方法相当于在每次迭代中对输入样本进行数据增强，然后进行数据集成，最后进行梯度计算.这种方法大大提高了对抗样本生成所需的时间和资源，违背了快速梯度符号方法的样本快速生成初衷.

3 本文算法

3.1 对抗样本噪声初始化

深度学习中，对网络权重进行初始化有利于模型的收敛.目前对抗噪声初始化方法仅有随机噪声初始化，本文使用像素偏移方法对噪声进行初始化处理.

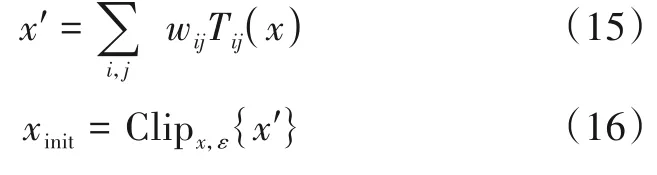
其中，Tij(x)表示将图像x位于(a，b)位置的像素值变换为(a-i，b-j)位置的像素值，且i，j取值范围为{-k，…，0，…，k}，wij为每次变换的权重，而Clipx，ε{x'}限制x'的范围并令xinit满足

3.2 基于准双曲动量方法的多次迭代快速梯度符号方法

Ma 等在优化领域提出了准双曲动量方法（Quasi-Hyperbolic Momentum，QHM）［18］，对比传统的动量方法，QHM引入了滑动平均系数v，其更新过程为

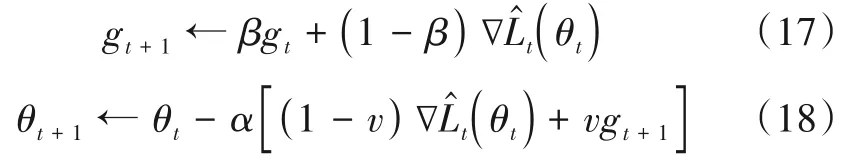
其中，β为动量系数.

本文将QHM 用于对抗样本生成，取代原有的MIFGSM，形成基于准双曲动量方法的多次迭代快速梯度符号方法（Quasi-Hyperbolic Momentum Iterative Fast Gradient Sign Method，QHMI-FGSM）.QHMI-FGSM 将式（6）、式（7）转化为

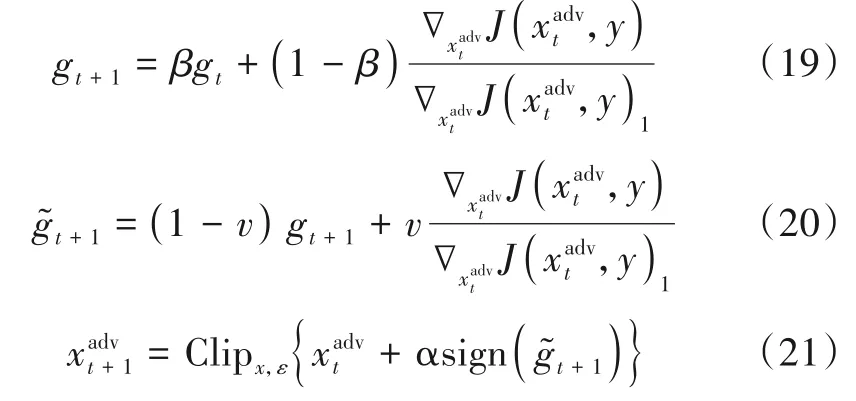
3.3 基于Adam-Nesterov 方法的多次迭代快速梯度符号方法

贾熹滨等在优化领域提出了AdaDelta-Nesterov 动量方法［19］，这种方法通过梯度的均方根（Root Mean Squared，RMS），对学习率进行了自适应约束，其过程为

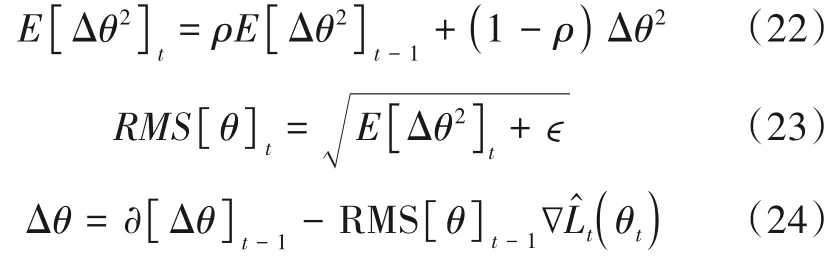
其中，E[Δθ2]t表示前t-1 次迭代所有梯度的平方和，RMS[θ]t表示前t-1次迭代所有梯度的均方根，ρ表示滑动平均系数，ϵ表示极小值.

本文将AdaDelta-Nesterov 方法应用于对抗样本生成中，形成基于AdaDelta-Nesterov 多次迭代快速梯度符号方法（AdaDelta-Nesterov Iterative Fast Gradient Sign Method，ADNI-FGSM）.ADNI-FGSM 在NI-FGSM 的基础上融入了自适应学习率，将式（8）优化为

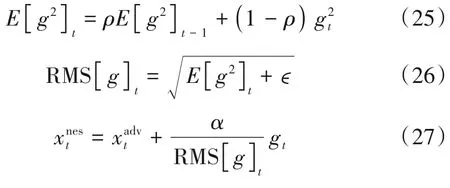
本文在ADNI-FGSM 的基础上，进一步提出基于Adam-Nesterov 多次迭代快速梯度符号方法（Adam-Nesterov Iterative Fast Gradient Sign Method，ANIFGSM），用于生成对抗样本.比较Adam［20］和AdaDelta［21］，Adam 在AdaDelta的基础上融入动量法，并修正一阶和二阶动量估计的偏差，ANI-FGSM可表示为

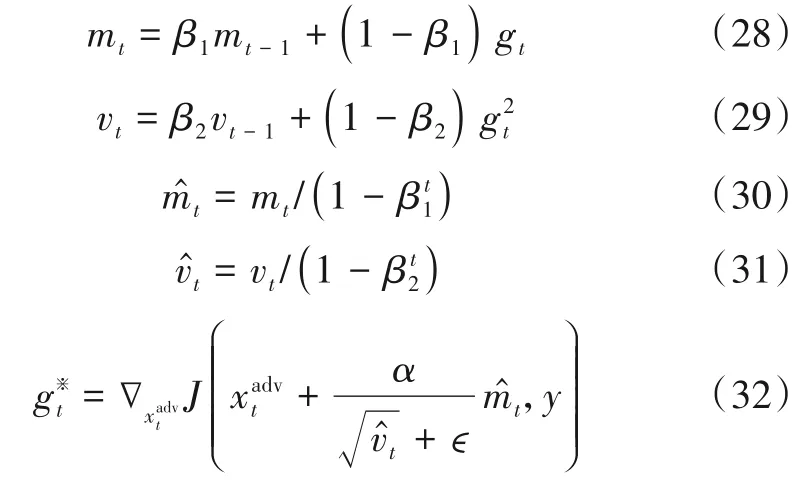
其中，mt和vt分别为一阶和二阶动量估计，和分别为一阶和二阶动量估计的修正项，β1和β2分别为动量系数和分别为动量项修正系数.实验中，本文令

3.2 节和3.3 节 的QHMI-FGSM 和ANI-FGSM 属于图1 中对抗样本生成框架中的两个部分.QHMI-FGSM进行梯度运算后用于噪声叠加，而ANI-FGSM 用于Nesterov项的生成.

3.4 对抗样本生成算法

本节以ANI-TI-DIQHM*（噪声初始化（3.1 节）、ANI-FGSM（3.3 节）、TIM、DIM、QHMI-FGSM（3.2 节）的组合）为例，其详细过程如算法1所示.

4 实验及结果分析

4.1 实验目标

如图1 所示，基于本文方法，实验目标为以下4 个方面：

（1）通过对比生成时间，验证本文方法对对抗样本生成效率的影响；

（2）通过实验，比较节3.3 中2 种方法ADNI-FGSM和ANI-FGSM的优劣；

（3）通过消融实验，验证本文方法对对抗样本迁移性能的影响；

（4）通过对比现有最好的攻击方法，验证本文方法的有效性.

4.2 实验设置

4.2.1 数据集

本文实验中使用的1000张样本取自ImageNet的测试集，同时也与NIPS 2017 对抗大赛中使用的数据集相同.实验中所有输入干净样本和输出对抗样本的大小均为299×299×3.

4.2.2 模型

实验共涉及13 个模型，其中4 个为Inception v3（Inc-v3）［22］，Inception v4（Inc-v4），Inception ResNet v2（IncRes-v2）［23］和ResNet v2-101（Res-v2-101）［1］，作为白盒模型用于生成对抗样本.另外9 个为Inc-v3ens3，Inc-v3ens4，IncResv2ens［6］，NIPS 2017 对抗大赛中排名前三的防御方法（HGD［7］、R&P［8］、NIPS-r3*），Feature Distillation［24］，Comdefend［25］和Randomized Smoothing［26］，作为黑盒模型用于测试对抗样本.防御模型中，Incv3ens3，Inc-v3ens4，IncResv2ens，HGD、R&P 和NIPS-r3是经典的防御方法，用于全部实验.而Feature Distillation，Comdefend 和Randomized Smoothing 是目前较为先进的防御方法，用于测试实验中较强攻击.

4.2.3 攻击组合

通常情况下，对不同方法进行组合能增强对抗样本的迁移性能.本文实验的组合都是节2.2 中不同方法的组合，并与本文的三种方法进行横向比较.各个攻击组合的具体解释如表1 所示.本文实验均在TI-DIM和NI-TI-DIM 这两个较强攻击组合的基础上进行，通过对抗样本生成效率、消融实验、单模型黑盒攻击和多模型集成黑盒攻击这四个方面，比较不同攻击组合的运行时间和黑盒攻击成功率.

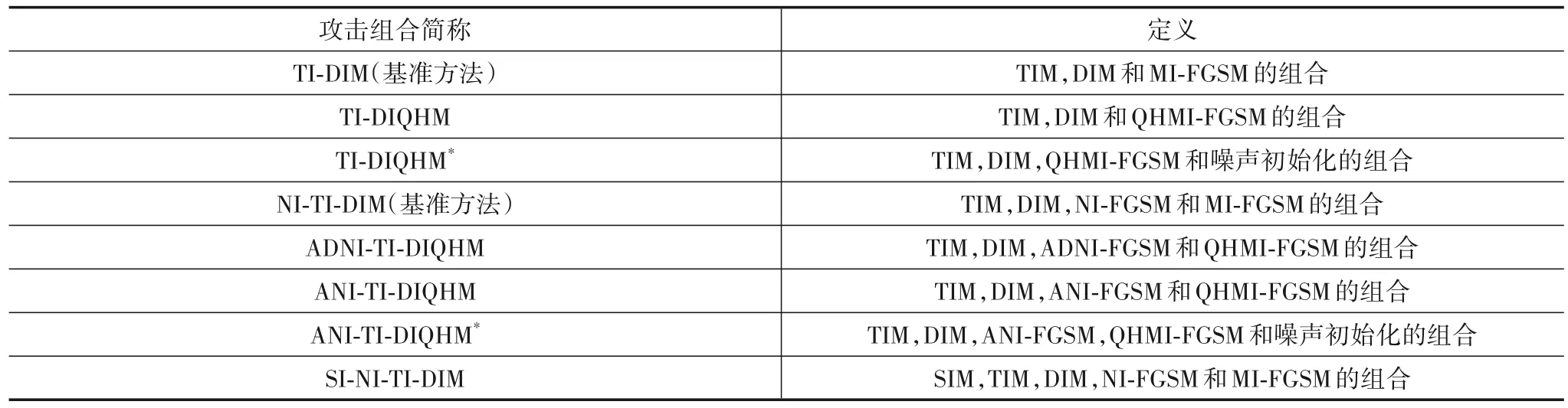
表1 攻击组合简称及其定义

4.2.4 损失函数与超参数

实验中所有生成方法所采用的损失函数都是交叉熵损失函数.所有实验设置最大扰动量ε为16，迭代次数T为10，步长α=ε/T，高斯核W大小为15×15，转换概率p为0.7，图像转换大小为330×330.本文方法的超参数则设置β=0.9，v=0.1，ρ=0.9，β1=0.12，β2=0.9，k=3.

4.3 攻击组合的生成效率

通常情况下，对抗样本生成存在运行时间和运算资源的限制，在同一条件下对比攻击组合的生成效率，具有现实意义.本文比较表1 中所有攻击组合的生成效率，实验设备使用的CPU 为i7-6850K，GPU 为GTX 1080 Ti，分别比较单模型黑盒攻击和多模型集成黑盒攻击.各攻击组合的生成效率（s）如表2 所示.可以发现，包含本文方法的攻击组合不会增加额外的运行时间，而包含SIM 的攻击组合SI-NI-DIM 和SI-NI-TI-DIM所需要的运行时间远超其他攻击组合.因此，单模型和多模型集成攻击实验中，将不包括SI-NI-DIM 和SI-NITI-DIM.

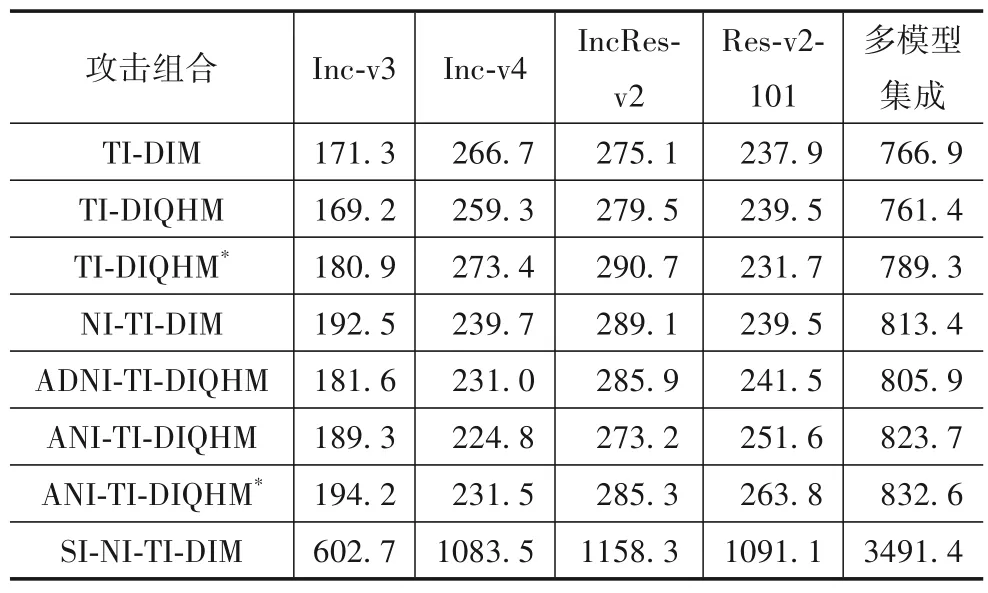
表2 生成效率/s

4.4 消融实验

本节通过消融实验，验证本文3种方法对对抗样本迁移性能的影响.实验以NI-TI-DIM 为基准方法，集成Inception v3，Inception v4，Inception ResNet v2 和ResNet v2-101 4个白盒模型，逐步添加本文方法来生成对抗样本，并攻击Inc-v3ens3，Inc-v3ens4，IncResv2ens这3个黑盒防御模型.如表3 所示，逐步添加本文提出的3 种方法后，对抗样本对黑盒防御模型的攻击成功率逐步增加.实验表明，本文的3 种方法都能提高对抗样本的迁移性.

表3 消融实验成功率/%

4.5 单模型黑盒攻击

本节通过对比黑盒攻击成功率，验证QHMI-FGSM和ANI-FGSM 分别替换MI-FGSM 和NI-FGSM 的有效性，同时验证噪声初始化的有效性，以及比较ADNIFGSM和ANI-FGSM.单模型黑盒攻击中，对比实验分别以Inception v3，Inception v4，Inception ResNet v2 和ResNet v2-101为目标模型，通过2组不同的攻击组合生成对抗样本，并攻击6个不同的黑盒防御模型.

2组攻击组合在单模型黑盒攻击中的成功率如表4和表5 所示，在不增加运行时间和运算资源的前提下，与MI-FGSM、NI-FGSM 相比，单模型黑盒攻击中QHMIFGSM 和ANI-FGSM 能和其他方法更好地组合，实现更高的黑盒攻击成功率，即生成的对抗样本具有更好的迁移性能.同时，噪声初始化能在此基础上，实现更高的黑盒攻击成功率.此外，ANI-FGSM 在单模型对抗样本生成中要优于ADNI-FGSM.

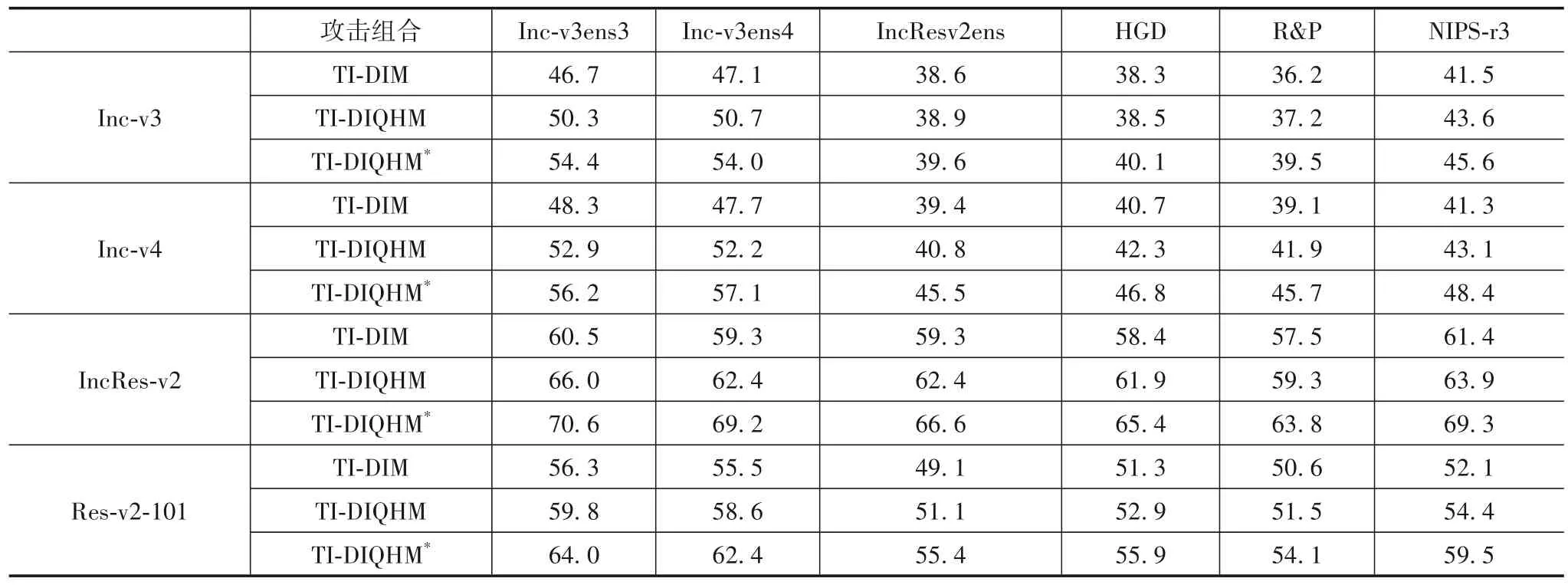
表4 TI-DIM，TI-DIQHM和TI-DIQHM*单模型黑盒攻击成功率/%

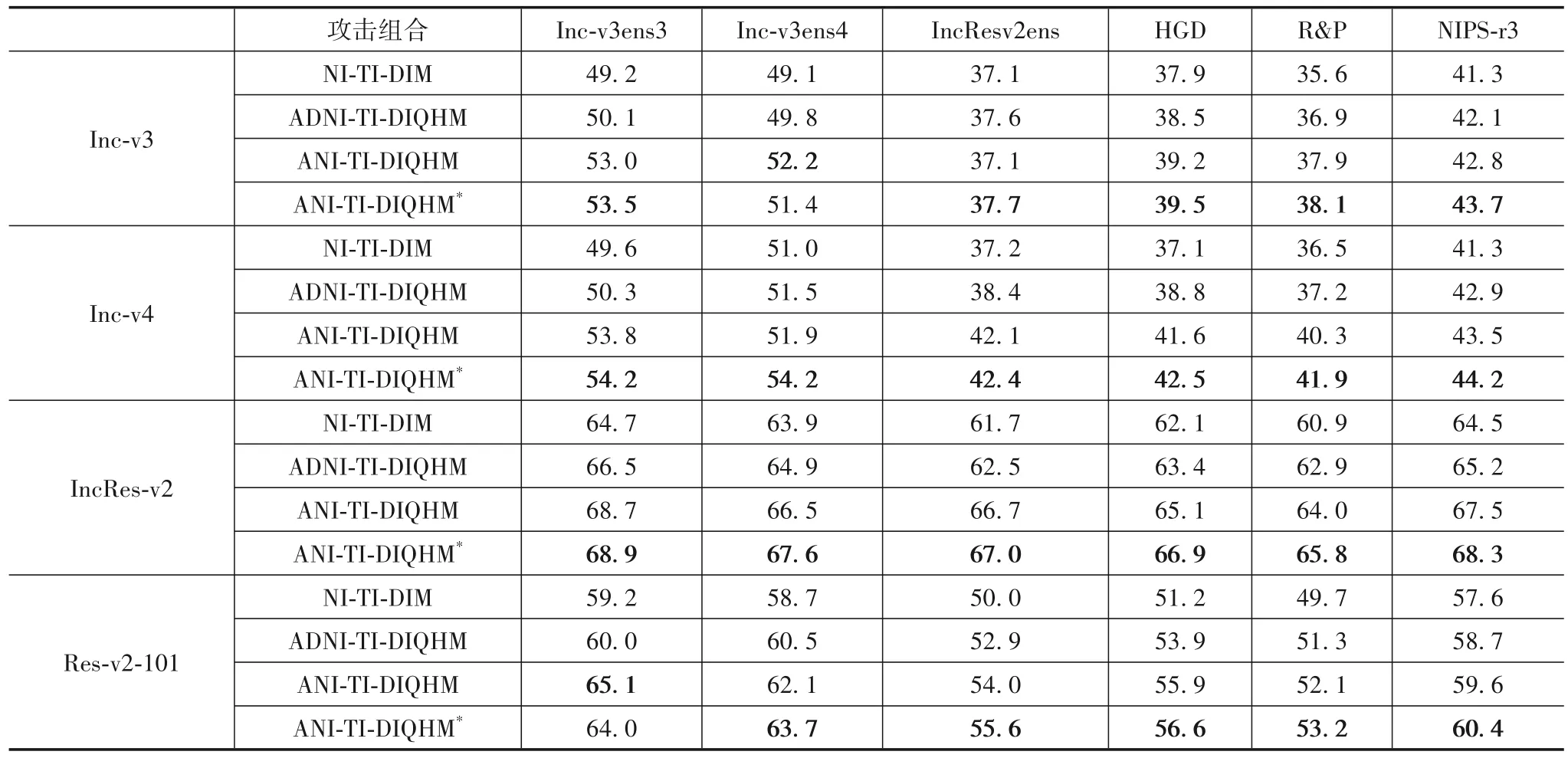
表5 NI-TI-DIM，ADNI-TI-DIQHM，ANI-TI-DIQHM和ANI-TI-DIQHM*单模型黑盒攻击成功率/%

4.6 多模型集成黑盒攻击

在多模型集成黑盒攻击条件下，本节验证QHMIFGSM 和ANI-FGSM 分别替换MI-FGSM 和NI-FGSM 的有效性，同时验证噪声初始化的有效性，以及比较ADNI-FGSM 和ANI-FGSM.实验以Inception v3，Inception v4，Inception ResNet v2 和ResNet v2-101 的集成模型为目标模型，通过不同的攻击组合生成对抗样本，并攻击个不同的黑盒防御模型.

多模型黑盒攻击中的成功率如表6 和表7 所示，与MI-FGSM 和NI-FGSM 比较，本文方法QHMI-FGSM 和ANI-FGSM 在多模型集成黑盒攻击中，能和其他攻击方法更好地组合，实现更高的黑盒攻击成功率.而本文提出的噪声初始化能提高黑盒攻击成功率.此外，ANIFGSM 在多模型集成攻击中要优于ADNI-FGSM.最强攻击组合ANI-TI-DIQHM*对经典防御方法和较为先进的防御方法的平均黑盒攻击成功率分别为88.68%和82.77%，均超过现有最高水平.

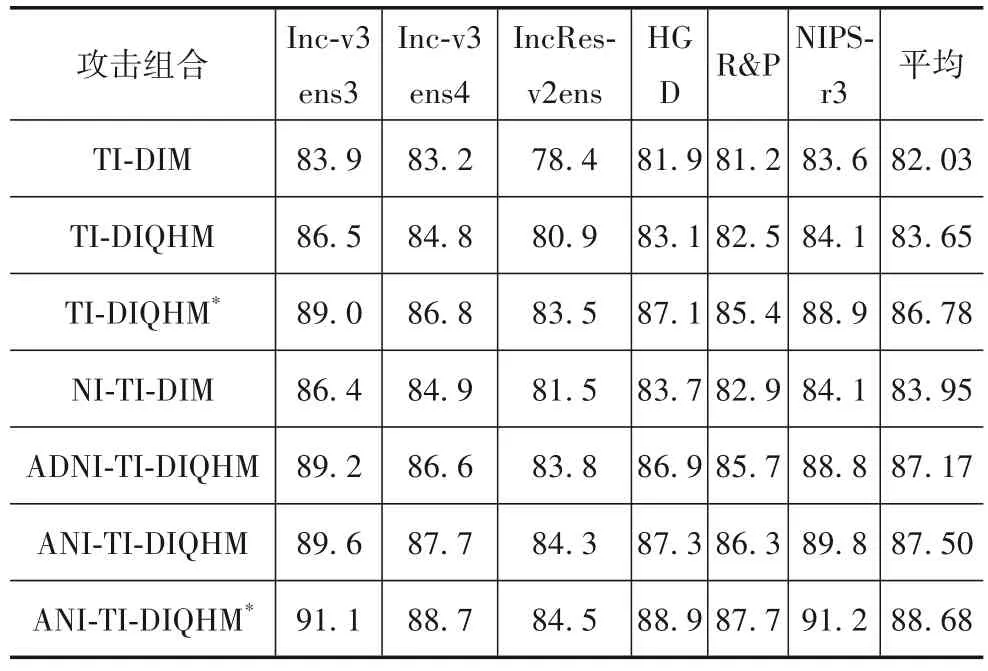
表6 多模型黑盒攻击对经典防御方法的成功率/%

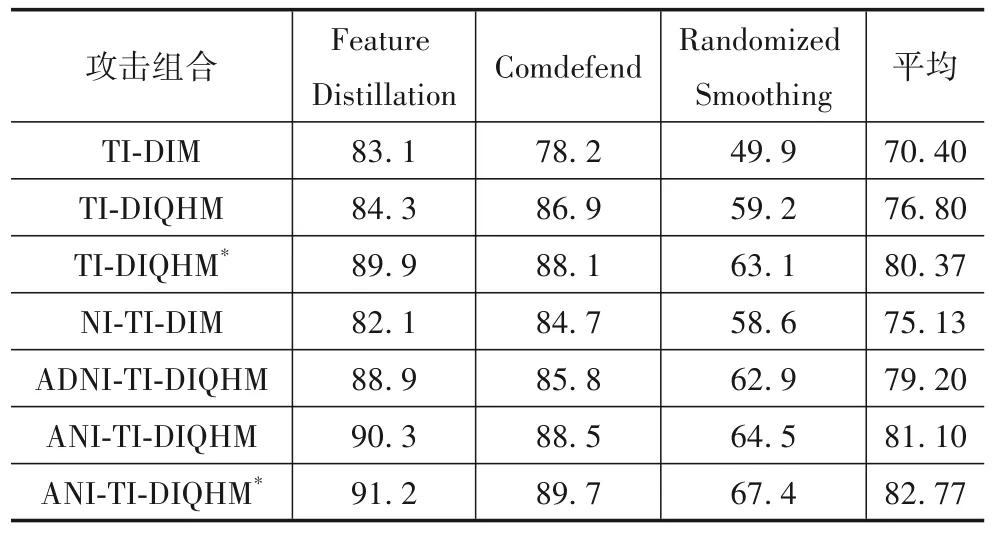
表7 多模型黑盒攻击对较为先进的防御方法的成功率/%

4.7 对抗样本扰动量

扰动量大小是对抗样本的一个重要衡量指标，尽管对抗样本满足‖xadv-x‖∞≤ε的约束，但本文的目标是在维持扰动量大小的前提下，令本文方法生成的对抗样本具有更高的黑盒攻击成功率.因此，本节通过比较不同方法所生成的对抗样本的平均扰动量，以及比较针对9个黑盒防御模型的平均成功率，来说明本文方法的有效性.不同方法所生成对抗样本的平均扰动量和针对9 个黑盒防御模型的平均成功率比较如图2 所示（ε=16）.

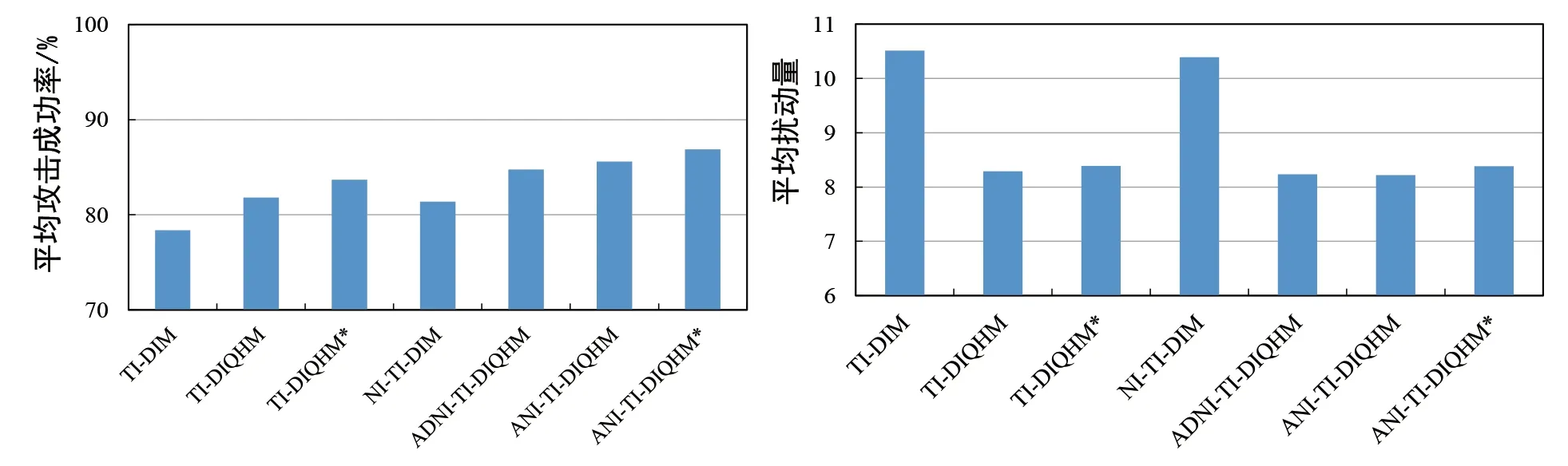
图2 多模型集成黑盒攻击对抗样本的平均成功率和平均扰动量

由图2 可以发现，对比TI-DIM 和NI-TI-DIM，本文方法不仅能提高对抗样本的黑盒攻击成功率，还能将对抗样本的平均扰动量降低10%以上.

4.8 对抗样本对比

为了验证图2的结果，本节对比不同方法生成的对抗样本（ε=16）.由图3 可以发现，本文方法所生成的对抗样本与TI-DIM，NI-TI-DIM 所生成的对抗样本相比，由于平均扰动量更低，其对抗噪声形成的条纹更淡.然而无论是现有方法TI-DIM 和NI-TI-DIM，还是本文方法，对比干净样本，对抗样本上的条纹都较为明显.显然，通过‖xadv-x‖∞≤ε去限制对抗样本的扰动量是不够的，平均扰动量可以作为参考指标之一.在接下来的工作中，维持黑盒攻击成功率，降低对抗样本的平均扰动量，使得对抗样本更具有威胁，是一项有意义的研究.

5 结论及展望

本文针对基于梯度的对抗样本生成方法，提出基于噪声初始化、Adam-Nesterov 方法和准双曲动量方法的对抗样本生成方法.本文对对抗噪声初始化进行研究，通过像素偏移方法来预先增强干净样本的攻击性能.同时，本文使用Adam-Nesterov 方法和准双曲动量方法来改进现有生成方法中的Nesterov 方法和动量方法，实现更高的黑盒攻击成功率.在不需要额外运行时间和运算资源的情况下，本文方法可以和其他的攻击方法组合，并显著提高了对抗样本的黑盒攻击成功率.实验表明，本文的最强攻击组合为ANI-TI-DIQHM*，其对经典防御方法的平均黑盒攻击成功率达到88.68%，对较为先进的防御方法的平均黑盒攻击成功率达到82.77%，均超过现有最高水平.