土仓压力与掘进参数相关性分析及预测模型

成晓元，凌静秀,，黄继辉，吴勉

(1.福建工程学院 机械与汽车工程学院, 福建 福州 350118;2.福建工程学院 福建省数控装备产业技术创新研究院，福建 福州 350118：3.中建海峡建设发展有限公司，福建 福州 350000)

土仓压力是保证土压平衡盾构机正常掘进的重要控制参数之一[1]，将其控制在合理的范围内，将有助于扼制施工过程中出现的地表沉降、隆起等问题[2-3]。盾构机掘进前需要提前设定土仓压力值，而在实际的施工过程中往往会按照施工经验设定土仓压力值，这对工程的安全和质量极为不利，合理预测土仓压力成为国内外学者的重点研究内容之一。

王洪新等[4]搭建了土压平衡盾构掘进过程的数理模型。上官子昌等[5]建立了推进速度等可控因素与土仓压力之间的映射关系。Liu等[6]基于小二乘支持向量机建立了土压预测模型。李守巨等[7]基于遗传算法对土仓压力进行预测。

盾构机在掘进过程中，由于地下环境的高复杂性和不确定性，影响土仓压力变化的因素众多。而以上的预测模型仅考虑与土仓压力相关的推进速度、螺旋机转速等5个可控因素，忽略了可能对土仓压力存在影响的其他因素，因此上述预测模型缺乏普遍性和准确性。

本文充分考虑在盾构掘进过程中可控因素以及其他因素，并分别与土仓压力进行相关性分析，得到和土仓压力相关性显著的因素作为预测模型LSTM的输入，预测下一环的土仓压力。

1 土仓压力与可控因素

土压平衡盾构机掘进面切削下来的泥土填满土仓，借助推进油缸的推力对掘进面加压，形成土仓压力，与掘进面上的水、土压力相抗衡。图1为土压平衡盾构机的力学模型。

图1 土仓压力力学模型

土压平衡盾构正常掘进过程中，当刀盘切削下来的泥土量和螺旋输送机的输土量相平衡时，就实现了掘进面的稳定。基于此种情况，王洪新等[4]根据土仓-螺旋输送机之间的数学模型(公式(1))、土仓内流量的连续性方程(公式(2))、盾构机掘进时的动力学方程(公式(3))和掘进面土压力和土仓内土压之间的关系(公式(4))，得到螺旋机转速、推进速度、总推力3个可控因素和土仓压力之间的关系，见公式(5)。

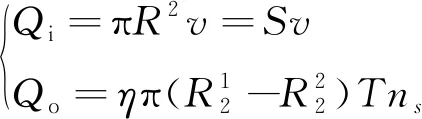
(1)

式中，Qi为土仓进土量，m3；v为盾构机掘进速度，mm/min；S为切削刀盘面积，m2；R为刀盘半径，mm；Qo为螺旋机出土量,m3；η为排土效率；A为螺旋机有效断面积，m2；T为螺旋机叶片的螺距，mm；ns为螺旋机转速，r/min；R1为螺旋机半径，mm；r2为螺旋机轴半径，mm。

(2)

式中，cep为土仓外泄露系数；p为土仓压力，MPa；po为土仓外泄露压力，MPa；Ve为土仓容积，m3；βe为土仓内渣土、液体等有效压缩系数。

盾构机正常掘进中掘进面上动力学方程：

F-(f+P)=ma

(3)

其中，F为盾构机推进过程中的总推力，kN；f为推进过程中遇到的总阻力，kN；P为掘进面上的土压，MPa；m为盾构质量，kN；a为掘进加速度，m/s2。

P=πR2λp

(4)

其中，λ是刀盘开口率，%。

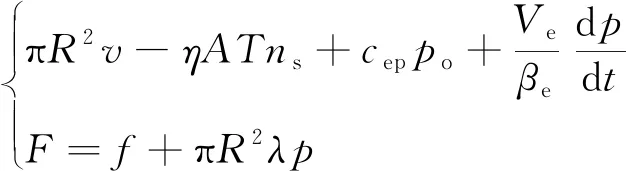
(5)

王洪新[8]分析了刀盘扭矩的影响因素，给出掘进速度、刀盘转速、刀盘扭矩和土仓压力之间的关系式，见公式(6)：

(6)

式中，Tn为刀盘扭矩，kN·m；vd为刀盘转速，r/min；φ为土体内摩擦角,(°)；c为掘进面土体黏聚力，kPa；D为刀盘直径，mm。

由以上公式可看出，盾构机正常掘进中，掘进速度v、螺旋机转速ns、总推力F、刀盘扭矩Tn、刀盘转速vd5个可控因素和土仓压力p之间具有非线性依赖关系。但盾构机掘进是一个复杂、多变量且各变量间存在强耦合的现象，仅靠5个可控因素建立的预测模型，难以精准预测土仓压力。

2 其他因素与土仓压力的相关性分析

2.1 数据选取和预处理

依托福州市在建的地铁4号线，实时监测采集数据并保存至数据库。针对掘进因素的选取及数据清洗，制定以下5条数据选取、预处理原则：

(1)非掘进过程中的数据给予删除，包括停机、机械故障和换装刀盘等状态，确保数据都是在盾构机正常掘进过程中检测到的。

(2)删除机械电机参数、润土流量、前后端里程、水平偏差、垂直偏差等因素。

(3)确保所取的掘进参数是在同一地质条件下的，排除因地质条件不同对土仓压力的影响。

(4)删除施工过程中因施工条件及工艺限制导致的人工大幅度改变掘进参数的数据。

(5)删除某一因素为0时所对应的实时其他因素的数据，确保各数据之间的对应关系。

通过以上原则，确定407～427环的数据作为研究对象，总计20环，2 579组数据，31个掘进因素，包括5个可控因素(推进速度、总推力、刀盘转速、刀盘扭矩、螺旋机转速)，26个不可控因素(A组推进压力、泡沫系统平均压力、螺旋机扭矩等)，列出全部因素见表1。

表1 各因素编号及与土仓压力的斯皮尔曼相关系数

对土仓压力和经过前文数据筛选原则挑选出来的26个不可控因素和5个可控因素共31个因素分别做相关性分析。在统计学中，常用皮尔逊相关系数，又称皮尔逊积矩相关系数。使用皮尔逊相关系数对变量有一个条件：适用于服从正态分布的连续型变量。

使用Origin绘图软件，分别对31个因素绘制正态分布图，判断各因素是否服从正态分布，结果见表1。并列举部分因素的正态分布图，如图2、3、4所示。

图2 推进速度正态分布图

图3 注浆孔A2注浆压力正态分布图

图4 铰接系统泵出口压力正态分布图

相较而言，推进速度、B组推进压力、螺旋机压力等11个因素符合正态分布的程度较高，刀盘转速、铰接系统泵出口压力、螺旋机油温等20个因素符合正态分布的程度较低，因此本文并不适合使用皮尔逊相关系数。

2.2 斯皮尔曼相关系数

斯皮尔曼等级相关系数，即Spearman相关系数，用于衡量定序变量之间的相关程度，且对变量之间没有具体要求。盾构机掘进参数中明显具有时间、顺序等特性，因此本文采用斯皮尔曼相关系数进行分析，公式见(7)。

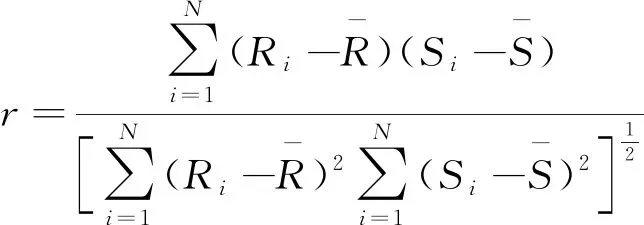
(7)

式中，Ri和Si分别是观测值i的取值等级;¯R、¯S分别是变量x和y的平均等级；N是观测值的总数。

通过SPSS软件对经过筛除、预处理后的1～31个因素编号，分别和土仓压力进行斯皮尔曼相关性分析，结果如表2所示。并通过柱状图更直观地表现各因素与土仓压力之间的相关性差异，如图5所示。

表2 |r|值与相关程度

图5 斯皮尔曼相关性分析结果

2.3 结果分析

斯皮尔曼相关系数值r介于-1～1之间，-1～0之间为负相关，0～1之间为正相关。其中，相关性系数的绝对值|r|越大，代表两因素间的相关性越强。一般情况下，可以通过表2来描述和判断相关程度[9]。

5个可控因素中，总推力和土仓压力的相关系数为0.681，强相关；螺旋机转速、推进速度、刀盘转速、刀盘扭矩对土仓压力的相关性为0.383、0.346、-0.265、0.253，弱相关。

B组推进压力、泡沫系统平均压力和土仓压力的相关性系数分别为0.591、0.418，中等相关强度；封前仓盾尾密封平均压力、封后仓盾尾密封平均压力、螺旋机油温、A组铰接油缸行程、C组铰接油缸行程分别和土仓压力之间的相关系数为0.370、0.367、-0.241、0.226、-0.216，弱相关。其他因素为极弱相关关系，可认为与土仓压力没有相关关系。

本文通过建立神经网络模型，将作为输入的因素分成两组，组一为5个可控因素、土仓压力；组二为5个可控因素、土仓压力、7个不可控因素。通过对比两组神经网络模型预测土仓压力的评价指标，来确定泡沫系统平均压力等其他因素是否会影响神经网络预测模型土仓压力的精度。

3 实验与分析

3.1 LSTM神经网络

长短期记忆神经网络LSTM通过遗忘门、输入门和输出门控制增加、遗弃信息，实现记忆和遗忘功能，结构如图6所示。相比于简单的RNN，LSTM单个模块更复杂，训练的参数更多，能很好解决BP神经网络在预测中容易出现的过拟合问题[10]，计算公式如式(8)。

图6 LSTM网络结构

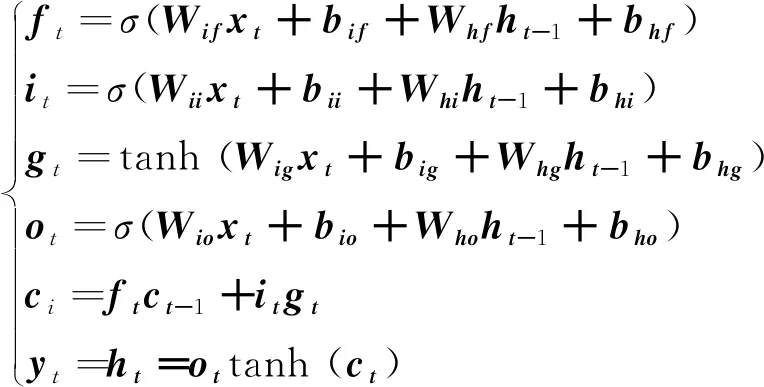
(8)

式中：xt是输入张量；yt、ht是输出张量；遗忘门ft、输入门it、单元状态gt、输出门ot分别对应不同的激活函数σ(x1)、σ(x2)、tanh(x3)、σ(x4)；wif、bif、wii、bii、wig、big、wio、bio是对于xt的线性变换参数矩阵；whf、bhf、whi、bhi、whg、bhg、who、bho是对于ht-1做线性变换的参数矩阵；记忆单元ci使用遗忘门ft控制上一时刻的隐含状态ct-1需要遗忘多少信息。

3.2 预测模型

LSTM模型一共4层，包括1个输入层、2个隐含层和1个输出层。从模型的角度来看，参数越多，预测模型的复杂程度就越高，在使用神经网络做预测时，为了追求对不同种类数据的高拟合效果，不断地增加层数和模型复杂程度，使得结果与训练数据拟合的越来越好，而在其他数据中效果越来越差，即拟合能力强、预测能力弱，这就陷入了过拟合陷阱。

为了实现本文对3组不同维度的输入因素预测土仓压力，同时防止出现过拟合现象，将407～426环数据作为训练集，427环作为验证集，分别进行归一化处理，然后将训练集数据分组次输入模型，使用Dropout和Early Stopping方法防止出现过拟合，并基于梯度下降算法[11]使用Adam算法对模型进行优化[12]。

经过数据训练和调超参，最终确定模型的输入层神经元数量为6、13；第一层、第二层的隐含层神经元数量为64；输出层神经元数量为1；权重衰减率0.001；优化学习率为0.05；Dropout随机率为0.8；迭代次数为500；循环早停数为5。

(9)

(10)

(11)

采用上述模型，将两组输入因素数据分别进行训练和预测，结果如图7所示，预测模型评价指标对比如表3。

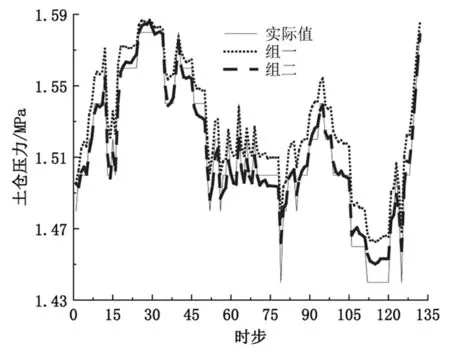
图7 福州地铁四号线427环土仓压力实际值与多因素分组预测值对比

表3 427环预测模型评价指标对比

通过前文的数据选取、预处理原则，选取783～803环的现场数据，进行与土仓压力的相关性分析，挑选出与土仓压力相关的因素，按照上文的分组原则，将783～802环数据作为训练集，803环作为验证集，结果对比如图8、表4所示。

表4 803环预测模型评价指标对比

图8 福州地铁四号线803环土仓压力实际值与多因素分组预测值对比

3.3 结果分析

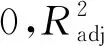
4 结论

1)总推力与土仓压力具有强相关强度关系；B组推进压力、泡沫系统平均压力和土仓压力之间具有中等强度关系；螺旋机转速、推进速度、刀盘转速、刀盘扭矩、封前仓盾尾密封平均压力、封后仓盾尾密封平均压力、螺旋机油温、A组铰接油缸行程、C组铰接油缸行程和土仓压力存在弱相关性。

2)在5个可控因素的基础上，增加与土仓压力具有相关关系的不可控因素作为输入，可实现对土仓压力的更精准预测。

3)通过选取783～802环数据作为训练集，803环作为验证集，验证了第二点结论，证明了本文预测模型的可靠性和有效性，为实现对盾构机施工前更精准预测与设定土仓压力值提供了参考。