基于模糊PID的盾构土仓压力控制研究
(石家庄铁道大学 机械工程学院,河北 石家庄 050043)
0 引言
土压平衡盾构机在掘进过程中,油缸推动旋转的刀盘将土体切削下来,土体随即顺着刀盘的开口进入土仓,再通过土仓内的螺旋输送机将土体运输出来。在整个掘进过程中要控制盾构土仓的压力来维持开挖面的稳定,如果土仓压力过大,就会使开挖面推力过大,从而导致地表隆起。反之土仓压力过小,造成开挖面推力不够,会产生地表塌陷。因此土仓压力是土压平衡盾构机在掘进时的一个重要参数,对实现地表变形有效控制具有重要意义。Liu et al[1]利用小二乘支持向量机的方法建立了以推进速度和螺旋机转速为参数的土压预测模型,仿真结果表明能够有效控制土压平衡。王林涛等[2]提出了推进速度前馈和土仓压力反馈的控制系统,经过试验表明响应速度较快,并且控制精度也较高。曹丽娟等[3]采用BP神经网络对盾构机土压进行控制,具有一定的稳定性和鲁棒性。刘博等[4]结合现场实际对土压平衡式盾构开挖面稳定机理和密封舱的土压控制进行了分析研究。本文主要设计了一种模糊PID控制土仓压力的方法,与传统PID对比,模糊PID控制方法响应速度更快,控制效果更优。
1 盾构土仓压力控制原理
土压平衡盾构机在施工过程中,土体的流向是:刀盘—土仓—螺旋机—皮带—渣土车,其中土仓是密闭空间,是由原始土层和盾构土仓的胸板构成的。要想控制土仓内的压力,必须控制好进入土仓的土体的速度,即盾构推进速度,和排除土仓土体的速度,即螺旋机转速。目前控制土仓压力常用的方法为人工调节法,根据盾构机显示屏反馈的土压数据人为调整螺旋输送机的转速,使土仓压力达到期望值。这种方法控制精度低,实时性不高。采用模糊控制策略的方法如图1所示。在盾构机掘进之前先设定好预期土仓压力,模糊控制器接受土仓实际压力、螺旋机转速和推进速度三者的反馈信号,通过计算给定合理的螺旋机转速和推进速度,使土仓的压力快速达到所设定压力。

图1 土仓压力控制原理
因为是对螺旋机速度和推进速度的控制,所以理论上存在3种控制方法,即控制螺旋机转速、控制推进速度和螺旋机转速和推进速度复合控制。控制螺旋机转速的方法,在推进过程中,不改变推进速度的大小,当土仓压力升高时,增大螺旋机转速;在土压降低时,减小螺旋机转速。控制推进速度是不改变螺旋机转速,调整推进速度来实现土仓压力的控制。第三种方法同时控制螺旋机转速和推进速度,控制方法优于前两种,控制速度快、精度高。图2为第三种土仓压力控制方法的原理方块图,土仓压力偏差通过补偿矫正器与给定电流和反馈的转速、位移信号做加减后,送给控制器,控制器计算给出合理的螺旋机转速信号和推进速度信号,从而土仓压力得到了控制。

图2 土仓压力控制原理方块图
2 数学模型的建立
2.1 土仓数学模型
盾构掘进过程中,土仓的压力主要取决于进入土仓内土的速度和排出土仓内土的速度。进入土仓内土的速度与土仓的横截面积A、推进速度v、土仓体积Vt等有关;排出土仓内土的速度与螺旋机排土效率η、螺旋机转速n(t)、螺旋机螺距S1、螺旋机有效排土面积AL等有关,因此土仓压力系统的数学模型为
(1)
根据Duncan-Chang土体的非线性本构关系,渣土的等效切变模量与土仓压力的关系为
(2)
式中,Pa为大气压力;a,n为待定系数。
将式(2)代入式(1)可得
(3)
将式(3)进行拉氏变换可得
(4)
根据式(4)可以绘制土仓模型的方框图如图3所示。

图3 土仓数学模型
2.2 比例电磁换向阀数学模型
在比例电磁换向阀线圈施加电流后电磁铁的静力方程为
FM=Kti-Kxxv
(5)
式中,i为通过线圈电流;Kt为电流比例系数;xv为阀芯位移;Kx为阀芯弹簧刚度。阀芯动态力平衡方程为[5]
(6)
式中,mv为阀芯质量;Dv为阀芯阻尼。对式(5)、式(6)进行拉氏变换,可得
FM(S)=(mvS2+DvS+Kv)Xv(S)
(7)
FM(S)=KtI(S)-KxXv(S)
(8)
联立式(7)、式(8)可得阀芯开度与电磁阀电流的关系
(9)
根据式(9)可绘出比例电磁换向阀模型的方框图如图4所示。

图4 比例电磁换向阀数学模型
2.3 液压马达的数学模型
根据液压系统的流量连续性方程,建立液压马达的数学模型为
(10)
式中,QL(S)为通过液压马达的流量;Ct为液压马达泄露系数;Vt为压缩容积;PL(S)为系统压力;βe为弹性模量;Dm为液压马达排量;θm为液压马达的转角位移。
由连续性方程可知,马达的流量与通过换向阀的流量相等,所以比例电磁换向阀的流量方程为
QL(S)=KvXv(S)-KcPL(S)
(11)
式中,Kv为流量比例系数;Xv(S)为阀芯位移;Kc为压力系数。液压马达的力矩平衡方程为
DmPL(S)=Jmθm(S)S2+Bmθm(S)S+Gθm(S)+TL
(12)
式中,Jm为等效转动惯量;Bm为阻尼系数;G为等效扭转刚度;TL为负载扭矩。 联立式(10)、式(11)和式(12)可得液压马达转角位移θm(S)与阀芯位移XV和负载扭矩TL的关系
(13)
式中,Kce为总流量压力系数。根据液压马达实际工作中,可以认为G=0、Bm=0,且马达轴的转角θm(S)与其转速N(S)之间的关系
(14)
可将式(13)转换为式(14),即马达轴的转速对阀芯位移和外界负载力矩的传递函数。
(15)

将式(15)转化为方框图如图5所示。
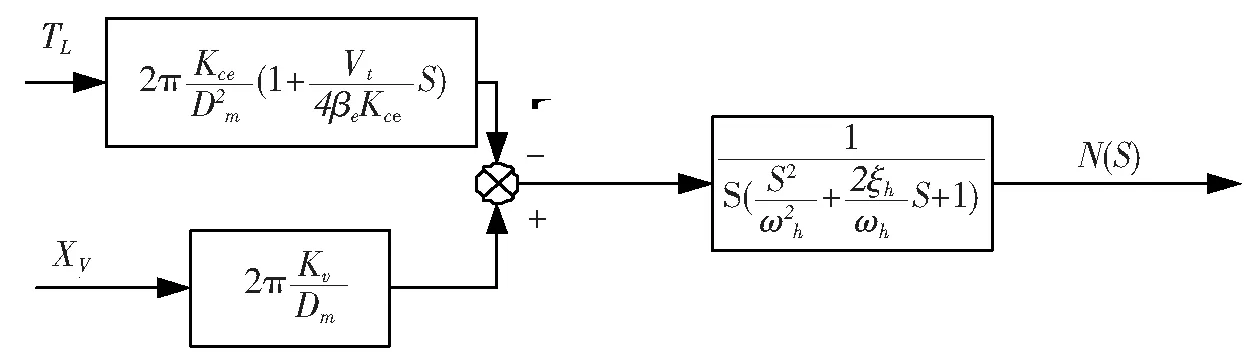
图5 液压马达数学模型
3 模糊PID仿真模型的建立
通过推导的土仓数学模型可知盾构的土仓压力主要取决于推进速度和螺旋机的转速,因此控制好这2个参数,就能保证土仓压力。由于盾构土仓压力系统具有非线性、控制环境复杂的特点,而在常规的PID控制中,各个因子是针对某一固定对象设定的,当控制环境发生变化时,不能在线实时调整,这就造成了传统PID对土仓压力控制的局限性。因此可以采用模糊PID在线对因子参数进行调整,以提高控制效果[6]。
3.1 模糊PID控制原理
二维模糊PID的控制原理图如图6所示,偏差E和偏差变化率EC为模糊PID的输入,通过控制规则和模糊推理的运算,得出增量值 ΔKp、 ΔKi、ΔKd用来在线调整PID控制器中Kp、Ki、Kd的值,使控制系统具有良好的控制性能。

图6 系统模糊PID控制结构图
在土仓压力控制系统中,将压力偏差E和压力的变化率EC作为模糊控制器的输入,模糊输出则是比例环节增益、微分环节增益和积分环节增益的增量值ΔKp、 ΔKi、ΔKd。
3.2 变量的模糊化和控制规则
定义偏差E、偏差变化率EC和ΔKp、 ΔKi、ΔKd的模糊子集为{NB,NM,NS,ZO,PS,PM,PB}。设定E、EC、ΔKp、 ΔKi、ΔKd的论域分别为:

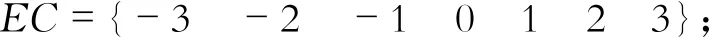
确定隶属函数的方法有直接法、推理法、F统计法等,均采用三角形隶属度函数[7],其中E和EC的隶属度函数形状如图7、图8所示。
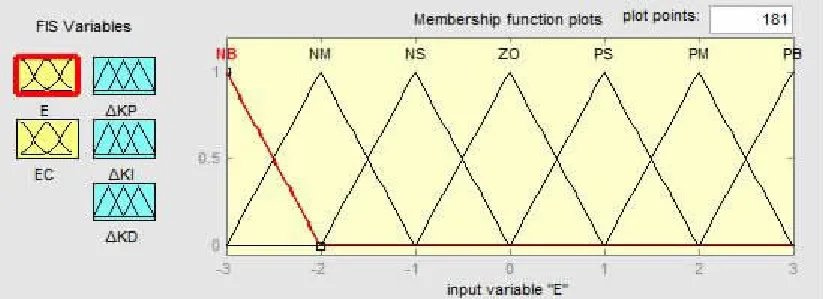
图7 偏差E的隶属度函数
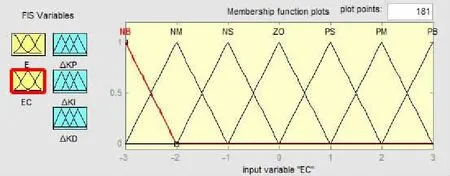
图8 偏差变化率EC的隶属度函数
根据实际经验,通过输入量E和EC来确定ΔKp、 ΔKi、ΔKd的模糊输出,表1~表3为ΔKp、 ΔKi、ΔKd的模糊控制规则表。

表1 ΔKp的控制规则表
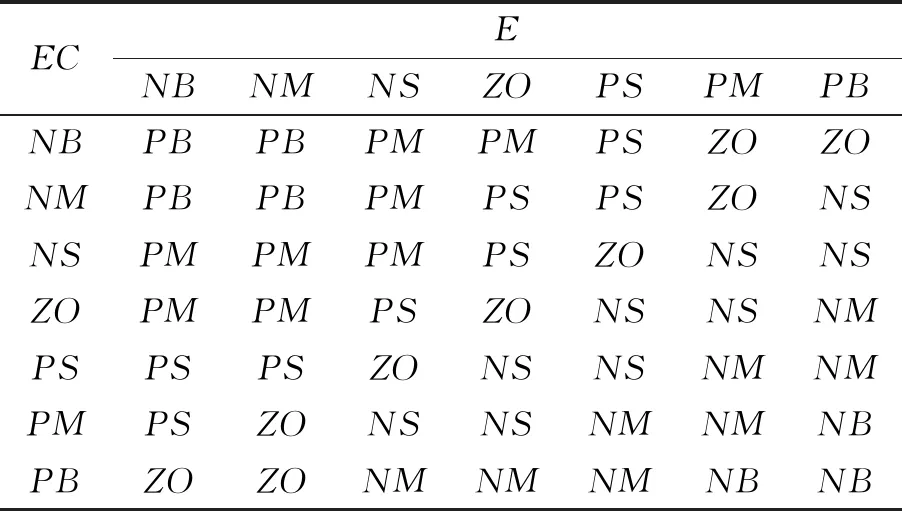
表2 ΔKi的控制规则表
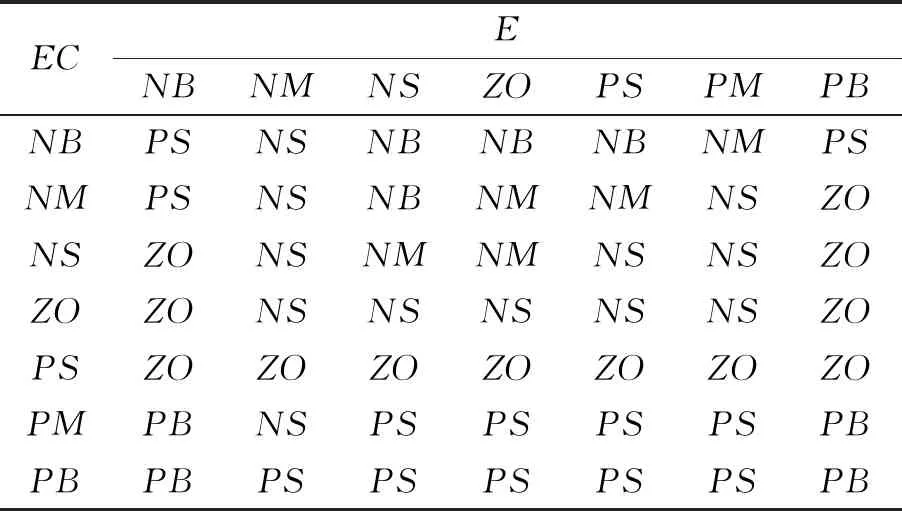
表3 ΔKd的控制规则表
根据表1~表3可以确定49条模糊关系,曲面观察器可以清楚直观地观察 ΔKp、 ΔKi、ΔKd的模糊关系[8],如图9所示。

图9 输出模糊规则曲面
4 仿真分析
采用石家庄铁道大学机械工程学院设计的盾构实验台参数进行仿真分析,实验台的具体参数见表4。

表4 实验台主要参数
根据图2土仓压力控制方块图和建立的土仓、比例换向阀、液压马达数学模型以及确定的模糊控制策略和实验台参数,在Matlab/Simulink软件中建立土压控制系统的仿真模型,如10图所示。系统分为常规PID和模糊PID 2部分,给推进系统施加阶跃信号,控制推进速度;给螺旋机系统施加常量,并将土压信号反馈给螺旋机系统,不断调整螺旋机转速,使土仓压力达到期望值。
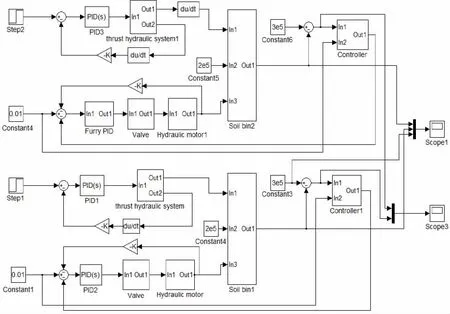
图10 土仓压力控制仿真程序
设定土压初始压力为0.2 bar,期望值为0.3 bar,推进系统的比例电磁换向阀电流变化为初值3 mA,终值4 mA的阶跃信号,图10中PID1和PID3控制推进速度,其参数均为Kp=3,ki=5,Kd=0;PID2控制螺旋机转速,参数为Kp=1.8,ki=0.5,Kd=0,其比例电磁换向阀的电流信号为8 mA;模糊PID的参数为Kp=0.6,ki=0.04,Kd=0采用重心法进行解模糊运算。仿真结果如图11~图12所示。
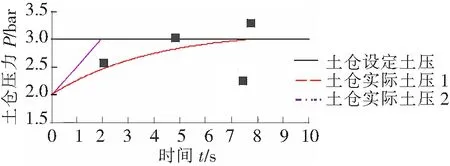
图11 土仓压力变化曲线
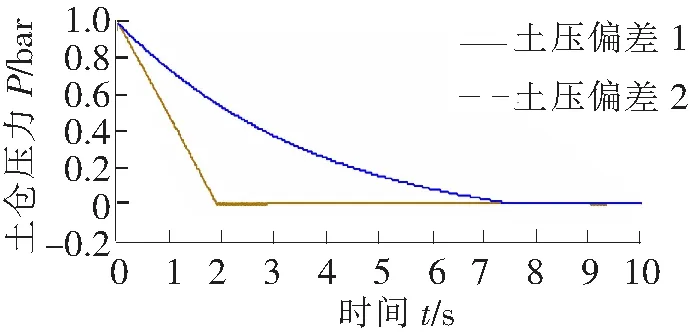
图12 土仓压力偏差变化曲线
在图11中,设定土仓压力设定压力值为3 bar。从图12中可以看出采用模糊PID控制土仓压力响应速度更快。
5 结论
根据各个系统的数学模型建立了土仓压力传统PID控制模型和模糊PID控制模型,通过仿真对比结果表明土仓压力控制采用模糊PID比采用传统PID收敛速度快、动态性能好。从偏差曲线来看,采用模糊PID消除偏差速度比较快,所用时间大约为1.9 s,而常规PID大约为7.8 s。所以与常规PID控制相比,模糊PID控制方法更适合用于土仓压力的控制。

