基于UM软件的高速铁路车桥系统振动响应参数分析
(云南省交通规划设计研究院,云南 昆明 650021)
高速铁路车辆过桥时一定要保证运行安全,因此对车桥系统进行了很多研究,Xia He et al对车桥振动在20世纪90年代就进行了研究工作[1]。夏禾等又进行了车桥墩相关规律的研究[2],并在此基础上利用子结构法把车-桥系统和桩土系统作为相互作用系统对考虑桩土的车桥系统进行了研究[3],后来又在车桥系统基础上研究了风-车-桥系统[4]和地震车桥系统[5]和波浪作用下车桥[6]的影响规律。张骞等对沪通长江大桥在风车桥作用下的响应进行了研究,得到了车辆运行的安全风速[7]。本文建立了车-桥耦合系统的振动分析模型,用UM软件进行计算分析,得到了列车速度、桥梁横向刚度、桥梁阻尼和列车数量对车桥系统响应影响规律。
1 车桥系统的建立
机车和车辆的模型各31个自由度,前后转向架、车体各5个自由度,即沉浮、横摆、侧滚、点头、摇头,轮对有4个自由度,即摇头、横摆、沉浮、侧滚,如图1。
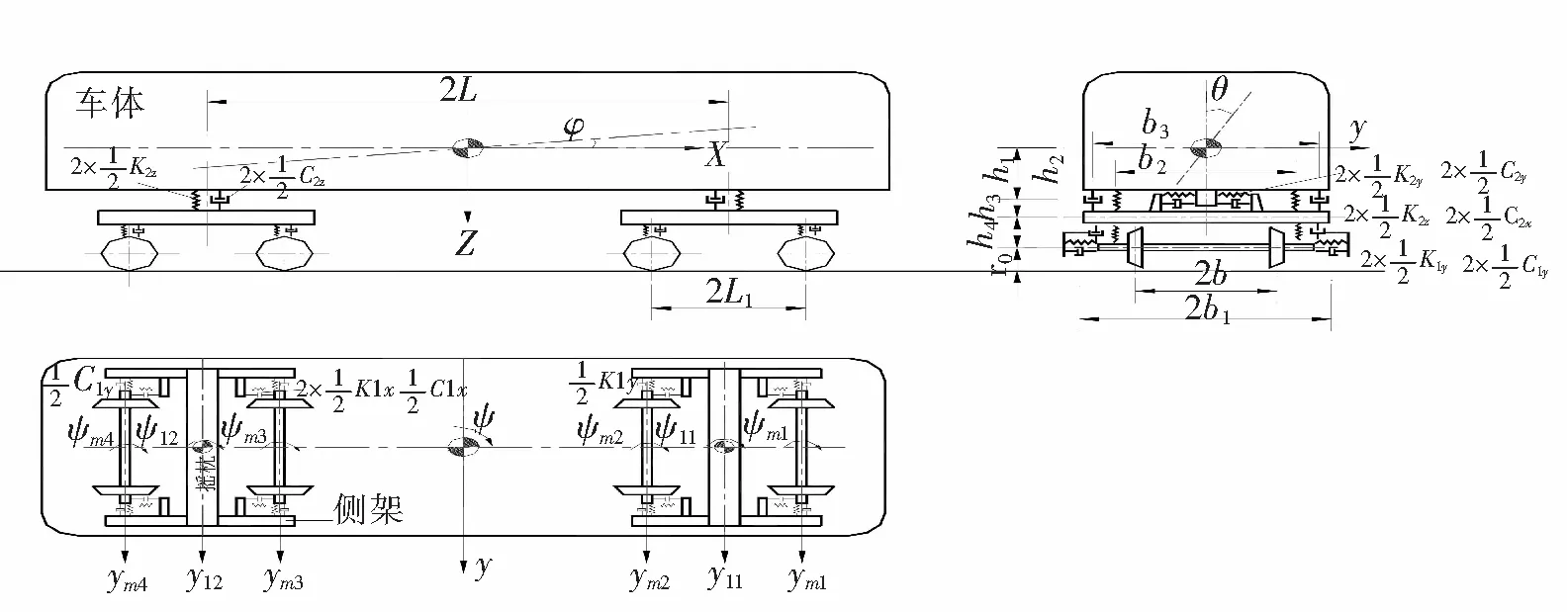
图1 车辆模型图
车辆的31个自由度表示如下:uv={zv,φv,θv,yv,ψv,zt1,φt1,θt1,yt1,ψt1,zt2,φt2,θt2,yt2,ψt2,zw1,θw1,yw1,ψw1,zw2,θw2,yw2,ψw2,zw3,θw3,yw3,ψw3,zw4θw4,yw4,ψw4}T。
z,φ,θ,y,ψ分别表示沉浮、点头、侧滚、横摆、摇头自由度;下标v表示车体的自由度,下标t表示转向架的自由度,下标wi表示轮对的自由度。
把车辆的31个自由度用动力学原理建立运动方程,矩阵形式如下
(1)
式中,{pv}表示施加在车辆上自由度的荷载向量。
桥梁用有限元法,桥梁采用梁单元模拟。桥梁振动方程为
(2)
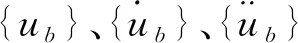
式(1)和式(2)中右端的pb和pv是在车辆、桥梁上的轮轨力。桥梁受到的荷载中包含车辆的自由度,车辆的轮轨力也包含桥梁的自由度,竖向轮轨力如下(采用赫兹非线性理论确定)
(3)
(4)
式中,pri(t)、pli(t)分别为左轨、右轨竖直方向作用力;w为轮对的轴重;zir(t)、zil(t)分别为t时刻对应第i个轮对处钢轨的竖向位移;ztj、θtj、φtj分别为转向架的沉浮、侧滚、点头自由度;G为轮轨接触常数,锥形踏面车轮G=4.57r0-0.149×10-8(m/N2/3), 磨耗形踏面车轮G=3.86r0-0.115×10-8(m/N2/3);Zwi(t)为t时刻第i个轮对的动位移。
蠕滑力按照车辆动力学的原理进行计算分析。
建立了车辆和桥梁的振动方程,用UM软件计算,采用Newmark-β或振形叠加法对车桥系统进行分析,能得到车桥系统参数的影响规律。
2 UM软件
Universa1 Mechanism(UM)程序是大型动力学计算程序,UM程序里提供车辆轨道的模型模块。还可以通过ANSYS软件的开发,实现外部子系统的开发和内部系统的车轨耦合,形成大的车桥系统进行模拟[8]。
3 车桥系统响应分析
为研究车桥系统响应的影响规律,桥梁采用24 m简支梁,桥梁支座采用简支约束,即一端约束X、Y、Z、RX,另一端约束Y、Z。轨道刚度相对桥梁刚度非常小,可以忽略。车辆采用我国的高速车辆。编组为:1动车+9拖车+动车。仿真开始前模型与桥梁相距50 m,速度分别取:180 km/h、200 km/h、220 km/h、250 km/h、270 km/h、300 km/h、320 km/h、350 km/h进行仿真。
3.1 桥梁自振特性分析
桥梁建模时选取的是ANSYS软件中的beam188单元,箱梁全长24 m,单元数为80个。建立完成的梁桥模型见图2。箱梁自振特性见表1。

图2 ANSYS箱梁模型图
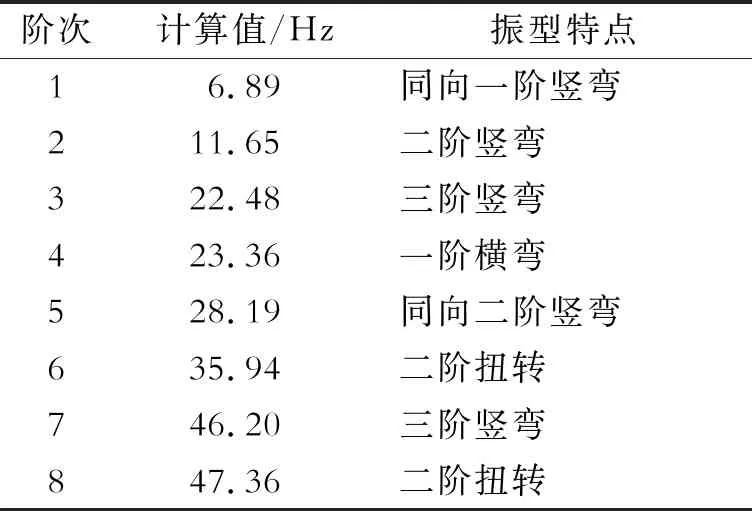
阶次 计算值/Hz振型特点16.89同向一阶竖弯211.65二阶竖弯322.48三阶竖弯423.36一阶横弯528.19同向二阶竖弯635.94二阶扭转746.20三阶竖弯847.36二阶扭转
计算桥梁结构的固有频率与振型计算结果见图3。
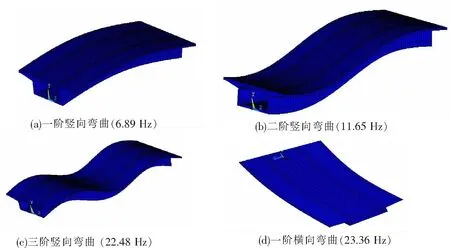
图3 梁体振型图
3.2 车桥系统动力响应列车速度影响
速度分别取:180 km/h、200 km/h、220 km/h、250 km/h、270 km/h、300 km/h、320 km/h、350 km/h进行仿真,结果如图4~图9。
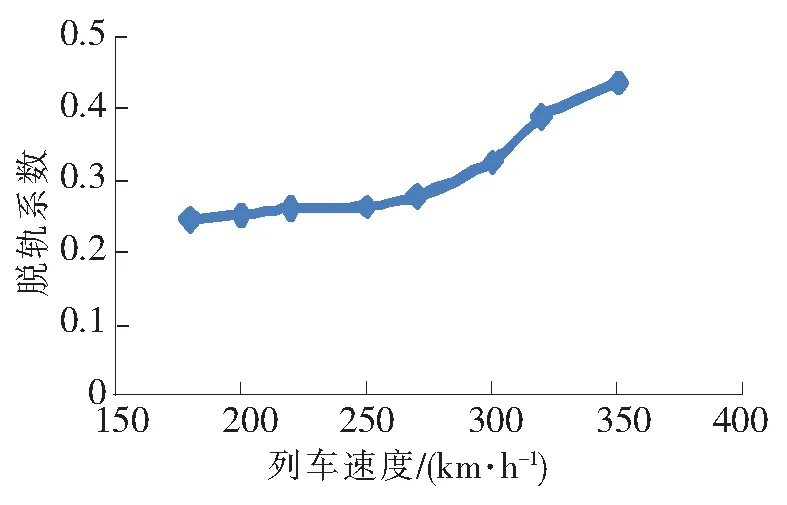
图4 脱轨系数变化曲线
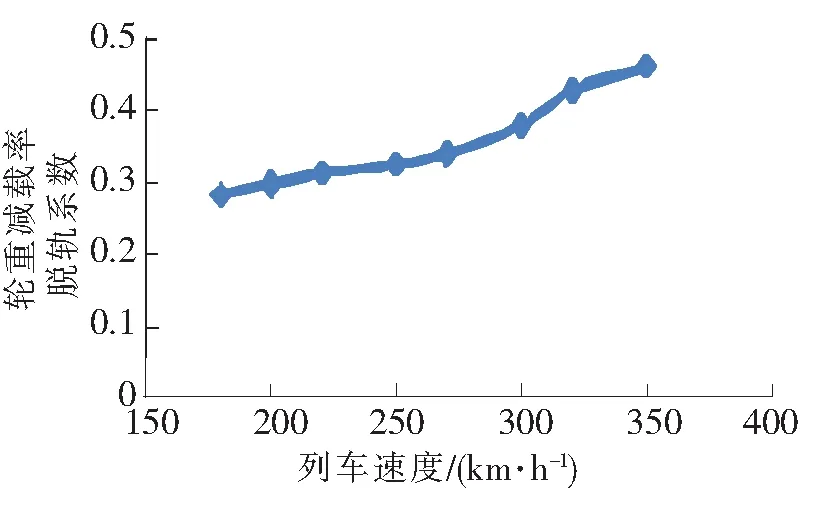
图5 轮重减载率变化曲线
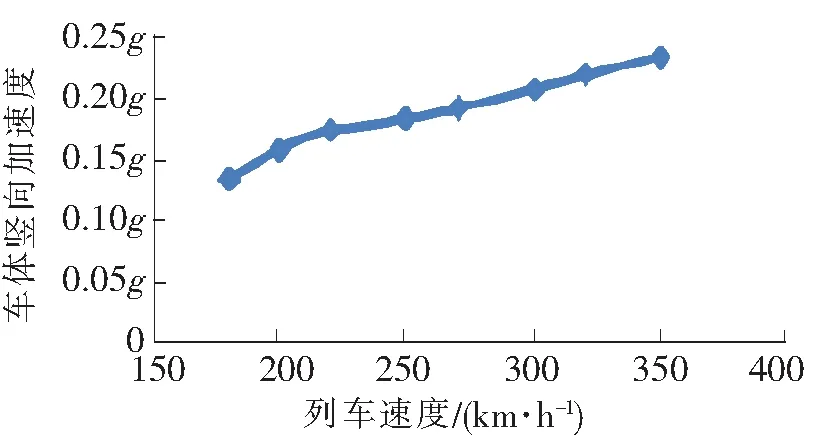
图6 车体竖向加速度变化曲线
图7 车体横向加速度变化曲线
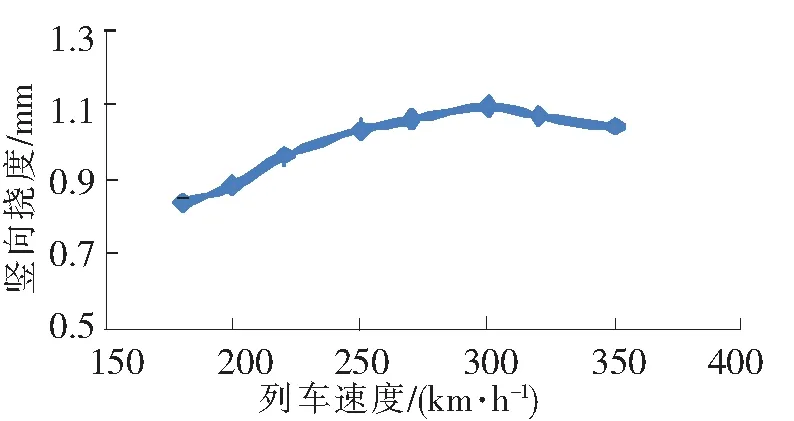
图8 桥梁跨中竖向位移变化曲线
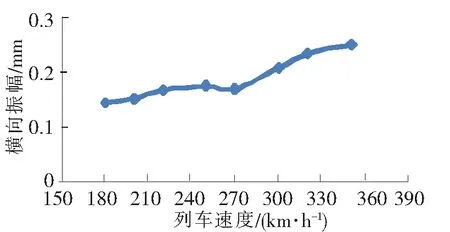
图9 桥梁跨中横向振幅变化曲线
从图中可得出以下结果。
(1)列车通过大桥时,随着列车行驶的车速提高动车减载率、脱轨系数、动车竖横向振动加速度变化趋势也增加,同时看出在模拟速度范围动力响应没有峰值。
(2)脱轨系数、轮重减载率在列车速度≤250 km/h时响应随车速的提高变化较慢,当车速>250 km/h,动力响应变化显著。
(3)桥梁的响应随列车速度的提高总体增大,但是变化关系不是线性的,峰值的位置和车辆和桥梁参数的匹配有关。
(4)桥梁竖向位移在车速度≥300 km/h时出现下降趋势,桥梁的竖向位移随速度增加不是一直增大。
3.3 车桥系统动力响应梁体横向刚度影响
为了比较刚度不同对桥梁动力响应的影响,分析了车速为200 km/h时不同刚度比0.15、0.45、0.75、1.25、1.55的动力响应。结果如图10~图11 所示。
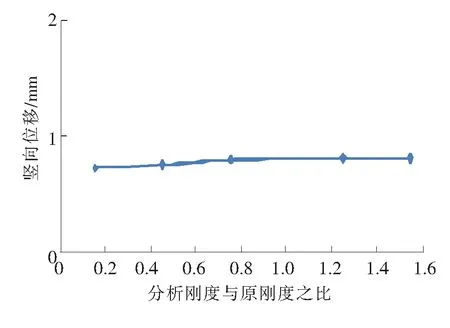
图10 竖向位移变化曲线
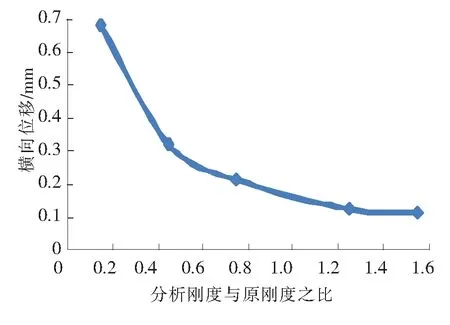
图11 横向振幅变化曲线
梁体跨中横向振幅随着横向刚度比增大而减小,而对竖向上位移值的变化基本没有影响。横向刚度对横向振幅值的影响到一定值时基本不再变化。因此应选择经济合理的桥梁刚度。
3.4 车桥系统动力响应阻尼影响
设定阻尼比的值2%、5%和 8%进行模拟对桥梁响应影响,列车时速为250 km/h,模拟结果如表2所示。

表2 阻尼比不同桥梁挠度最大值
从表2可知,当增大结构的阻尼比后,桥梁跨中的动力响应相对减小。阻尼比对桥梁加速度的变化率要大于位移的变化率,因此阻尼对加速度更加敏感。
3.5 车桥系统动力响应车辆数量影响
现实中根据列车类型不同,其所挂载的车辆数目也存在差异。现在高铁列车多是8节或16节,现取车辆数目分别为2、4、6、8、10、12、14、16、18、20进行仿真,研究在不同车辆数目条件下,梁体的动力响应情况结果如图12~图15所示。由图可以得出以下结果。
(1)随着车辆数目增加梁体跨中竖向位移的最大值有小幅度上升,但总体数值变化不大。说明车辆数目不是影响桥梁竖向位移的主要因素。
(2)桥梁横向振幅最大值随着车辆数目的增加而增大的幅度不是很明显,车辆数量到8节以后横向响应基本不变。
(3)梁体动力响应受车辆数量的影响不大,列车数量是影响桥梁响应的次要因素。
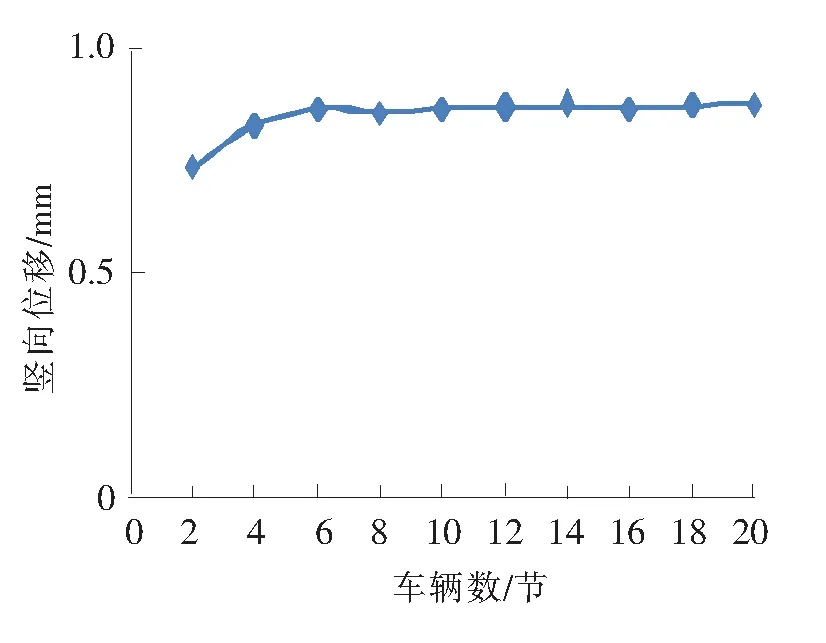
图12 跨中竖向位移变化曲线
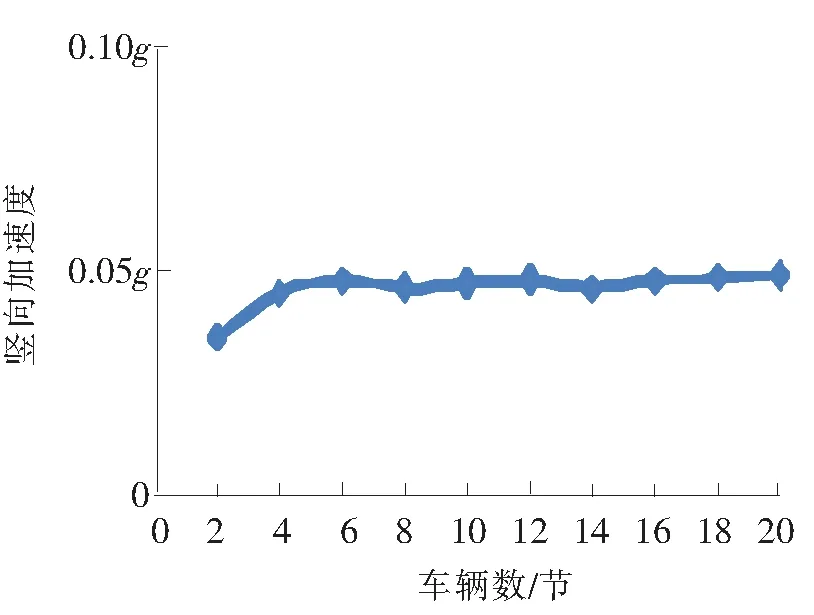
图13 跨中竖向加速度变化曲线
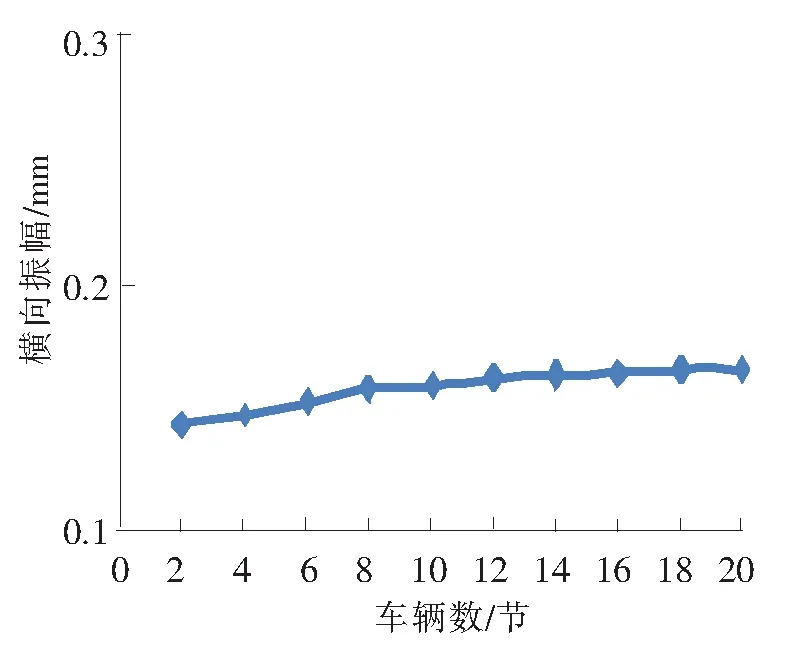
图14 跨中横向振幅变化曲线
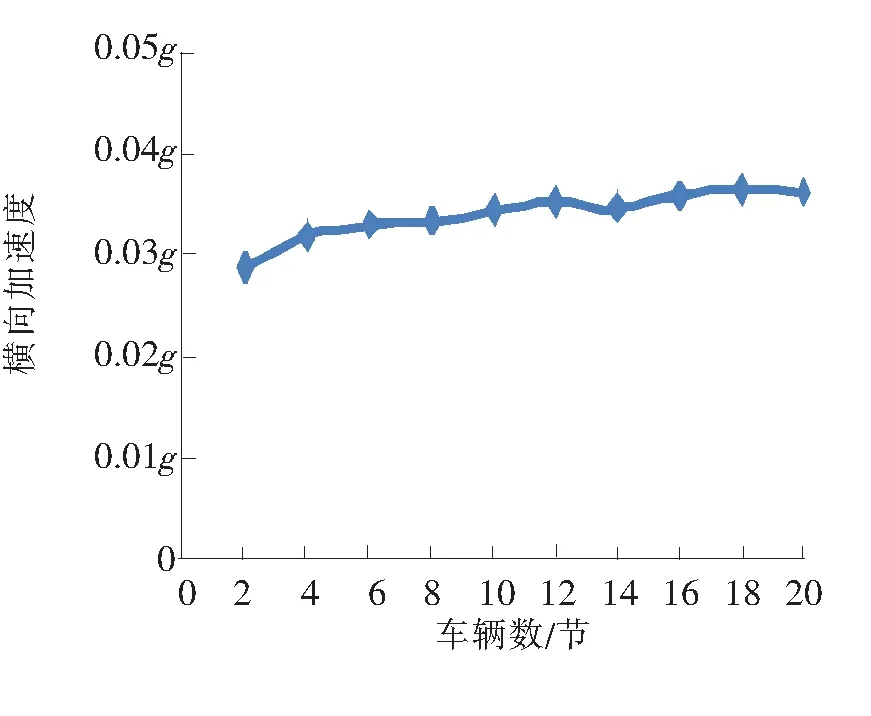
图15 横向加速度变化曲线
4 结论
通过对车桥响应的分析得到以下结论。
(1)随着速度的提高,车辆和桥梁动力响应总体呈增大趋势,但不是线性增加,响应大小和车辆与桥梁的匹配参数有关,因此对不同的车辆和桥梁应具体分析。
(2)横向刚度对桥梁的横向响应有影响,随着刚度的增大横向位移减小,而对竖向响应没有影响,系统是弱耦合系统。
(3)随着阻尼的增大,桥梁的动力响应减小,跨中加速度对阻尼变化更加敏感。
(4)列车挂载数量不是影响桥梁响应的主要因素。
(在此特别感谢石家庄铁道大学信丽华老师在论文仿真计算方面提供的帮助。)
——走进广东富华重工制造有限公司

