基于BP神经网络和最小二乘支持向量机的灰熔点预测和对比

时浩，肖海平*，刘彦鹏

（1. 华北电力大学能源动力与机械工程学院，北京市 昌平区 102206；2. 中国大唐集团科学技术研究院有限公司火力发电技术研究院，北京市 石景山区 100040）

0 引言

煤灰熔点是电站锅炉安全运行的重要影响因素之一。由于煤炭来源渠道多、煤质不稳定及考虑经济因素，电厂实际使用煤种常为混煤，且偏离设计煤种，灰熔点无法在线预测，威胁锅炉安全运行。

通常认为，煤灰熔点与灰成分中SiO2、Al2O3、Fe2O3、TiO2、CaO、MgO、Na2O、K2O 等组分含量密切相关[1-2]，经验公式的预测准确度不尽如人意，并且混煤灰熔点不符合各煤种灰熔点的简单线性加权叠加。因此，建立灰成分-灰熔点数学模型是灰熔点预测的重要方式。

操岳峰等[3]通过回归分析法提出了流动温度(flowing temperature，FT)的优化公式，该公式对山西、内蒙古地区的煤有较好的预测效果。Chehreh 等[4]通过多变量回归和自适应神经模糊技术建立了流动温度的经验回归公式，相关系数达到0.95。林德平[5]利用支持向量机预测软化温度(softening temperature，ST)，通过研究发现在小样本中添加实验数据可以有效提高预测精度。李清毅等[6]通过网格搜索参数寻优，发现支持向量机对单煤和混煤的预测精度高，误差不超过3%。赵显桥等[7]利用12 组ST 数据对支持向量机和神经网络模型进行了预测对比，结果发现支持向量机预测单煤和混煤更准确。Liang 等[8]建立了3 层BP 神经网络(BP neural network，BPNN)，通过研究发现变形温度(deformation temperature，DT)预测最大相对误差为6.67%，远低于线性回归。蒋绍坚等[9]通过Elman 神经网络预测了烟煤与生物质混燃的灰熔点，最大误差仅2.26%。

然而，现有研究常忽略SO3对灰熔点的影响以及碱酸比等结渣评判指标的重要参考作用，且样本数量少，有一定特殊性。本文针对某电厂生产过程所遇问题，利用BPNN 和最小二乘支持向量 机 (least squares support vector machine，LSSVM)建立2种灰熔点预测模型，且对2种预测结果进行对比分析，为该电厂实际煤种灰熔点和受热面结渣预测提供参考。

1 煤种数据整理与预处理

煤种数据来源于前人的研究、不同电厂设计煤种数据以及按照国家标准GB/T 219—2008测定的典型煤种数据，所用的灰熔点数据在氧化性气氛下测得。

采用灰锥法测定灰熔点，首先研磨煤样并筛分至200 目以下，平铺在瓷舟中，利用马弗炉按照GB 212—77 在815 ℃下制成煤样。根据国标GB/T 219—2008 规定的煤灰熔融性的测定方法，灰锥试样为三角锥体，高20 mm，底为边长7 mm的正三角形，锥体的一侧面垂直于底面。将做好的灰锥竖直固定于灰锥托板上，再将托板置于刚玉舟上，放入河南鹤壁博海公司生产的HR-4A灰熔点测定仪中测定灰熔点。所测定的某电厂部分实际用煤的灰成分和灰熔点如表1 所示，其中灰成分以氧化物质量分数计。

表1 某电厂部分用煤灰成分、DT和STTab.1 Ash composition,DT and ST of partial coal in a power plant

实际生产过程中，发现飞灰SO3含量对灰熔点具有较大影响。高硫煤燃烧过程中产生大量SO2气体，其中一部分会结合碱金属生成气态的硫酸盐等物质，900 ℃左右会在相对低温的水冷壁凝结[10]。冷凝的熔融态碱金属硫酸盐极易与附着在管壁的灰尘发生硅铝酸化反应，在1 100 ℃左右生成低熔点的长石类、霞石类矿物，从而导致变形温度的大幅度降低[11]。对于高硫高碱煤，SO3对灰熔点的影响尤为重要。而1 300 ℃以上硫酸盐基本分解，可认为对软化温度的影响不大。故综合考虑，将飞灰中SO3含量列为影响变形温度的因素。

另外，碱酸比、硅铝比、沾污指数、硅铝和可以由灰成分计算得出，作为结渣评判的常用指标，对预测结渣有重要参考作用，故在本研究中被考虑为DT和ST的影响因素。

此外，该电厂实际应用的一种ST经验公式如式(1)—(5)所示，计算结果称为第一类ST 指标，计算方法见文献[12]。

定义经验参数：

当SiO2质量分数大于60%，A12O3质量分数不大于30%，且Fe2O3的质量分数大于15%时，煤灰熔点ST可表示为

当SiO2质量分数大于60%时，煤灰熔点的ST可表示为

由于其计算结果经实践检验接近实际ST，故将该指标和参数a列为影响ST的自变量。

以上所有计算得出的数据称为煤灰复合系数。整理后，因变量DT及其自变量列于表2和表3，每一个DT对应9种灰成分和4个复合系数，共13个自变量、91组数据。

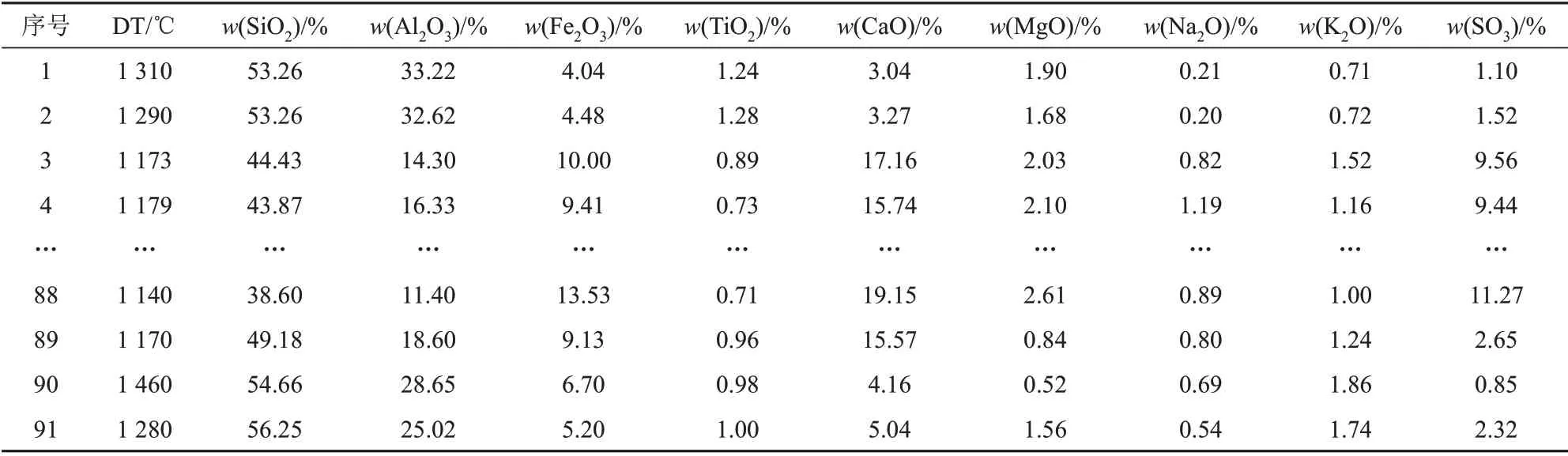
表2 煤灰变形温度与灰成分Tab.2 DT and ash composition of coal ash

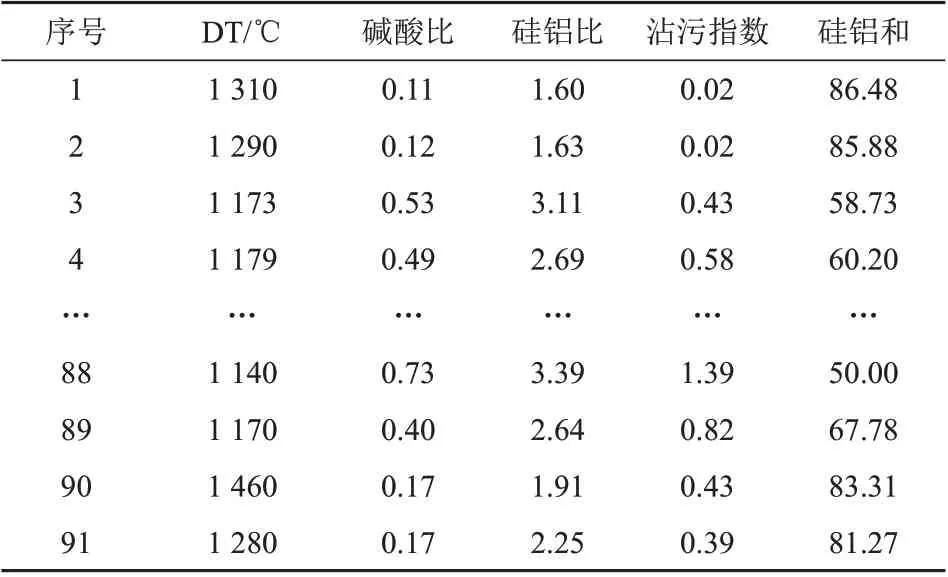
表3 煤灰变形温度与复合系数Tab.3 DT and compound coefficient of coal ash

因变量ST 及其自变量列于表4 和表5，每一个ST对应8种灰成分和6个复合系数，共14个自变量、60组数据。

表4 煤灰软化温度与灰成分Tab.4 ST and ash composition of coal ash

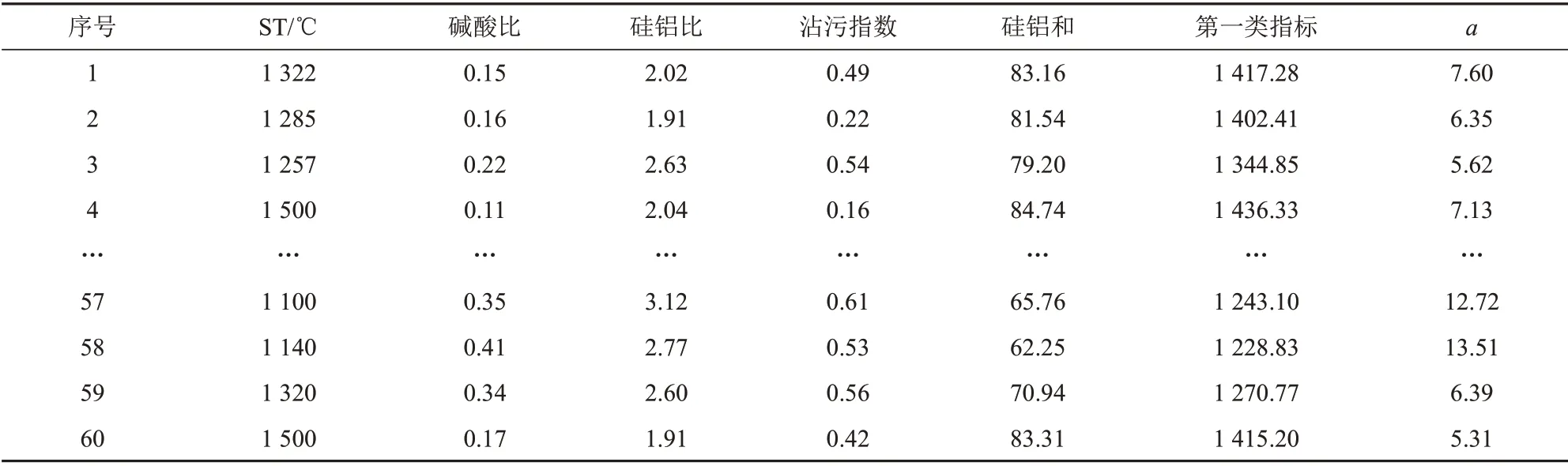
表5 煤灰软化温度与复合系数Tab.5 ST and compound coefficient of coal ash

2 煤灰熔点数学模型

2.1 BPNN模型建立

BPNN 采用标准梯度下降的误差逆传播(error back propagation)的学习方式，能够实现从输入到输出的复杂映射。由于本研究中样本数量较少，故采用单隐含层的3 层结构。输入层的传输函数为tansig函数，神经元个数为3；隐层的传输函数为purelin函数，神经元个数为2；输出层传输函数为purelin函数，神经元个数为1。设定训练目标为10-7，同时迭代上限设定为1 000 次，训练算法选取带有动量项的自适应学习算法(gdx)，可以在一定程度上避免局部陷入极值。

DT预测共91个样本，选定1—76号样本为训练集，77—91 号样本为测试集。ST 预测共60 个样本，选定1—50 号样本为训练集，51—60 号样本为测试集。利用划分的训练集和测试集分别对DT和ST进行预测。

2.2 LSSVM模型建立

LSSVM是将支持向量机中的不等式约束替换为等式约束，相比之下计算效率更高。选用的核函数为广泛使用且计算简便的高斯核函数(RBF)：

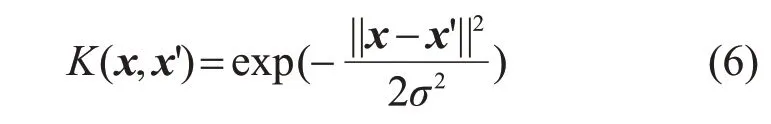
该LSSVM模型内有2个参数，即模型自带的惩罚系数C和高斯核函数的σ2。C越大，模型对误差的适应力越差，容易过拟合，反之则欠拟合；σ2越大，则越容易欠拟合，无法保证训练的准确率，从而影响预测。利用网格搜索交叉验证算法对C和σ2进行参数寻优。设定C网格范围为0.5～2 000，σ2网格范围为0.5～100，获得不同参数对(C,σ2)，然后进行交叉验证，设定为5折。评价函数设定为均方误差(mean square error，MSE)，当均方误差取最小值时，得到最优参数对(11.7,5.1)。

训练集和测试集划分同神经网络模型，用于对比2种模型的优劣。

3 预测结果对比与分析

3.1 DT预测结果分析

对于灰熔点预测结果，利用线性回归方法和标准残差、相对误差2个指标进行评价。

图1是2种模型预测DT的线性回归分析结果。BPNN模型和LSSVM模型的线性回归相关系数分别为0.923 87 和0.917 18，表明13 个变量与DT 有较好的线性相关性，且BPNN 模型线性相关性略好于LSSVM模型。

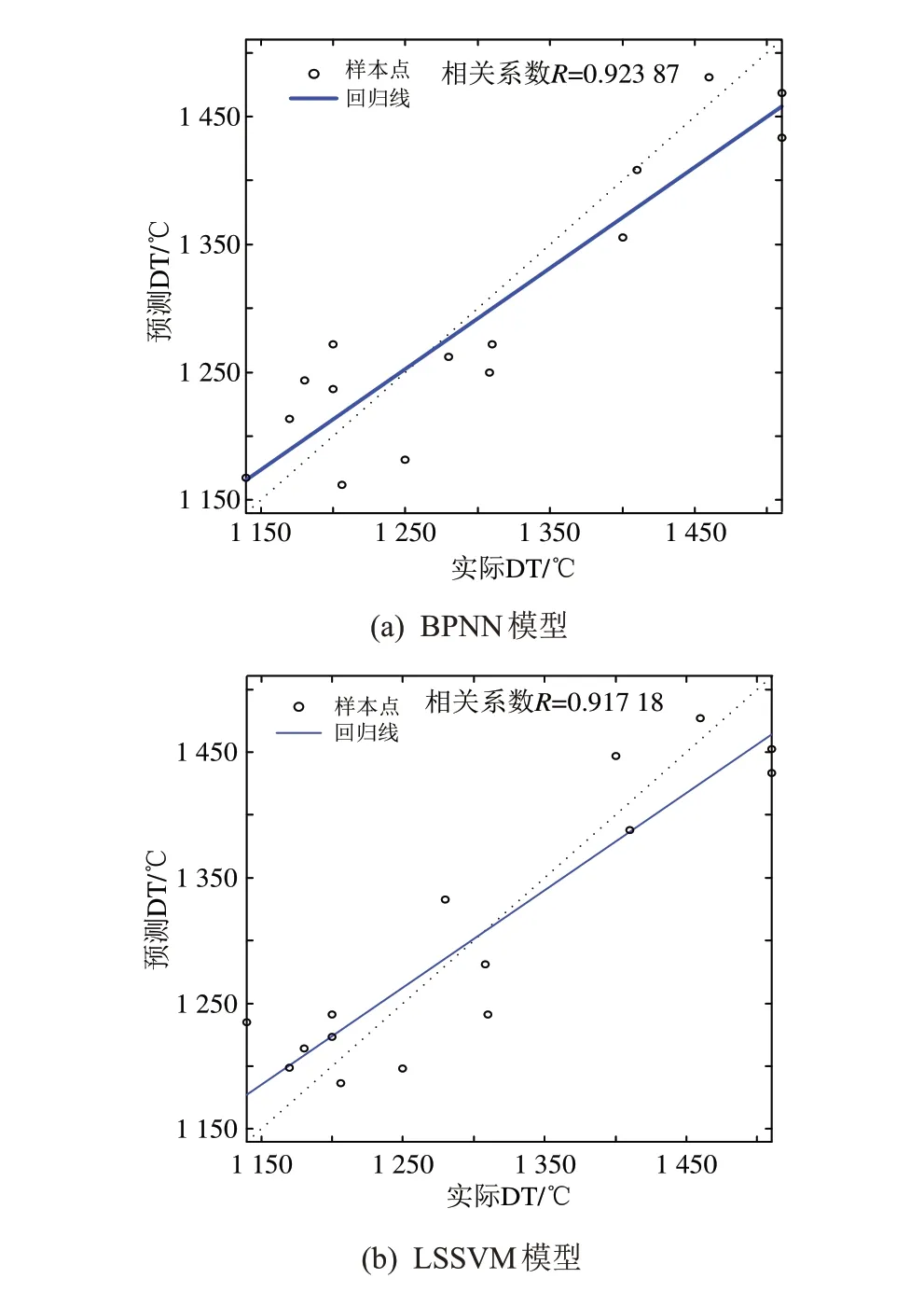
图1 DT预测线性回归分析结果Fig.1 Linear regression analysis results of DT prediction

图2 为2 种模型预测DT 的标准残差。可以看出，测试集所有样本预测结果的标准残差均落在[-2,2]的95%置信区间内，标准残差点的分布无明显规律，均匀落在0 的两侧，表明预测结果误差服从正态分布，具有很好的随机性，这说明描述DT 和13 个变量之间的回归模型是合理的，有较强的线性相关性。虽然3 号、5 号和14 号测试集样本的标准残差落在95%置信区间内，但标准残差较大，在追求预测精度时可作为存疑点剔除。

图2 DT预测结果的标准残差Fig.2 Standardized residual of DT prediction results

2 种模型预测DT 的相对误差如图3 所示。可以看出，2 种模型绝大多数预测值的相对误差都控制在5%以内，并且分布都比较平均，BPNN模型平均相对误差为3.40%，LSSVM 模型平均相对误差为3.41%。LSSVM 模型中12 号测试集样本相对误差最大，达到8.32%，而通过BPNN 模型预测得到的相对误差为2.40%，因此将2 种模型预测结果进行综合考虑，可以得到相对准确的预测数据。对于平均1 200 ℃的DT，其平均预测误差约为40 ℃，电厂可以根据运行实际调整灰熔点安全裕度。

图3 DT预测结果的相对误差Fig.3 Relative error of DT prediction results

总体上，2种模型对DT的预测精度均较好，说明将煤灰SO3含量和结渣评判指标列为自变量合理，13个变量与DT都有比较好的线性相关性。综合考虑2种模型的预测结果，在实际生产过程中为DT留出50 ℃的安全裕度，可以有效减轻和避免结渣。

3.2 ST预测结果分析

图4 是ST 预测的线性回归分析结果。DT 样本总数为91 个，而ST 仅为60 个。在训练样本更少的情况下，2 种预测模型的回归方程斜率相对于DT明显较小，并且2种模型线性相关系数有较大差距，BPNN 模型仅为0.904 26，而LSSVM 模型达到了0.950 52，表明预测ST所使用的14个变量在LSSVM模型中具有更好的线性相关性，预测效果更佳。

图4 ST预测的线性回归分析结果Fig.4 Linear regression analysis results of ST prediction

图5 是ST 预测结果的标准残差。与DT 预测相同，所有点落在了95%置信区间[-2,2]中，表明无明显异常数据点。所有标准残差点均匀分布在0 的两侧，表明回归模型建立合理，误差随机性很好。2种预测结果中，6号、7号和10号测试集样本都具有比较大的标准残差，若要提高精度，需要对原始数据进行核实查验。

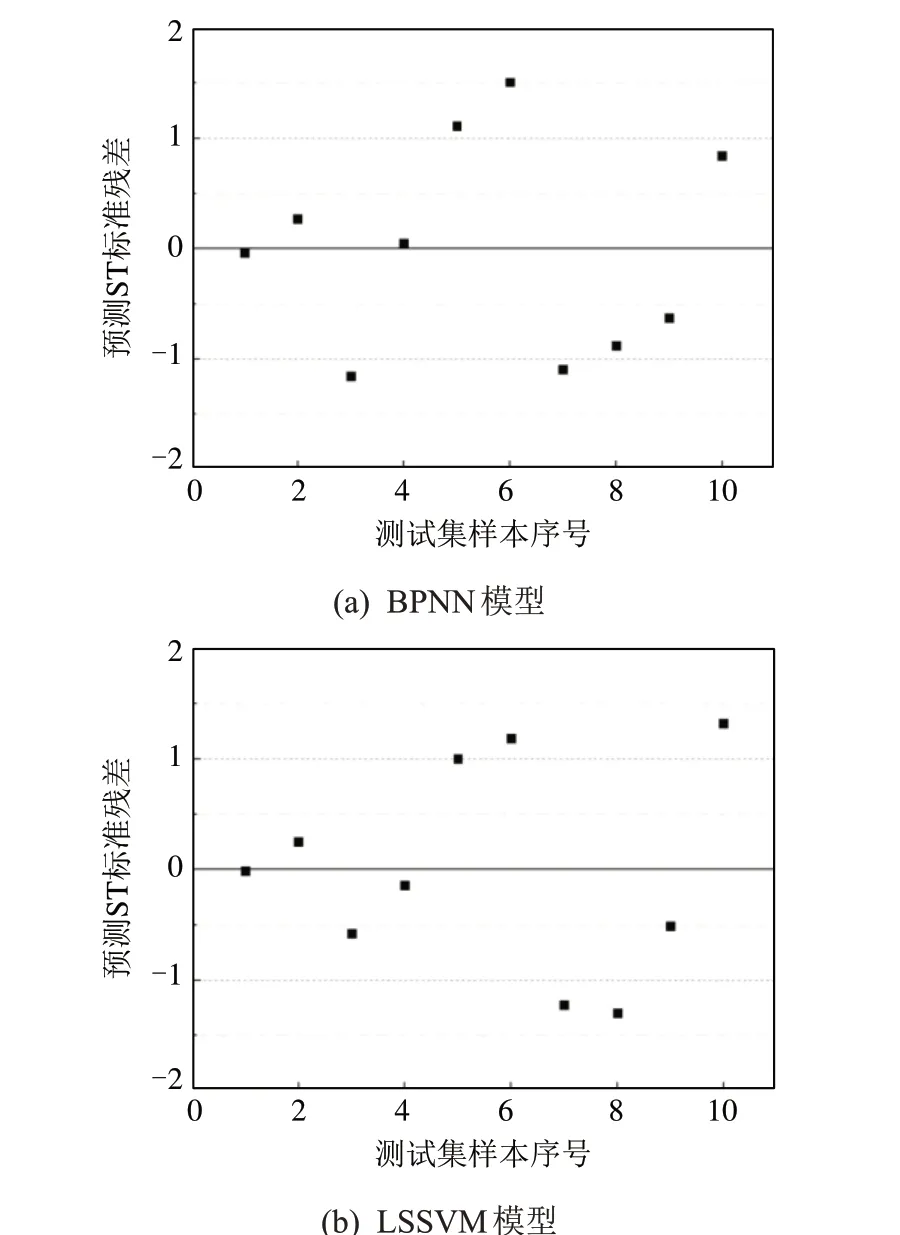
图5 ST预测结果的标准残差Fig.5 Standardized residual of ST prediction results

图6 是ST 预测结果的相对误差。相对于DT而言，ST 预测模型的相对误差较大，BPNN 和LSSVM 模型平均预测相对误差分别为5.01%和4.98%。结合标准残差分析，7 号数据为存疑点，是2 种预测模型相对误差的最大值，约7.5%。BPNN 得出的预测误差有一半超过了6.4%，而LSSVM 模型相对误差集中在5%以内，这意味着BPNN 预测结果大概率为高误差。对于平均1 300 ℃的ST，LSSVM 模型的预测精度比BPNN高1.4%，约20 ℃，整体平均误差达到了65 ℃，在实际生产过程中需要70 ℃左右的安全裕量。结合线性回归分析和标准残差分析得出，样本数据大体准确，但是受制于小样本，无法完全训练出14个自变量和因变量ST的线性关系。

图6 ST预测结果的相对误差Fig.6 Relative error of ST prediction results

对于ST，14 个自变量在LSSVM 模型中能够训练得出更高的线性相关度，比BPNN 模型更适合ST预测，泛化能力更强，其预测精度比BPNN模型高大约20 ℃，需要ST 留出70 ℃的安全裕度。首先，从算法原理角度，BPNN 训练之前需对初始输入量、各层权值以及各层偏置进行初始化，初值对于训练结果有一定影响[13]。其次，BPNN 算法不断的迭代造成过训练现象，引起训练振荡[14]。此外，小样本使网络识别能力不足，对未训练过的样本预测结果不好[15]。而LSSVM基于支持向量机，将输入矢量投射到高维空间，将原问题转化为多维线性目标问题[16]，再将SVM 的不等式约束转化为线性约束，避免复杂迭代和局部极小值，泛化能力强，更适合小样本预测。在生产过程中不断补充数据库、筛查数据以及剔除坏点，都能有效提高模型的预测精度。

4 结论

以灰成分中金属氧化物、SO3含量和结渣评判指标为自变量，DT和ST为因变量，建立了BPNN和LSSVM两种灰熔点预测模型，较好地实现了灰熔点的预测，通过研究和分析得到以下结论：

1）对于样本数据较多的DT，BPNN 和LSSVM 模型预测精度接近；而对于小样本ST，LSSVM的计算效率更高，预测精度和泛化能力更强，适合小样本预测。

2）样本数量越多，训练和预测效果越好。在条件允许的情况下，若能测得各煤种的精确数据，通过不断修正和补充训练数据库，能够有效提高2种预测模型的精度。

3）综合利用BPNN 和LSSVM 预测模型，可以为电厂配煤掺烧等提供较精确的灰熔点预测，从而减轻和防止受热面结渣，对锅炉的安全和经济运行具有重要意义。