10 MW中压六相直驱永磁风电机组最大功率跟踪策略研究

赵海川，金书辉，王欢，于世鹏，白茹，邢作霞

（1. 沈阳工业大学电气工程学院，辽宁省 沈阳市 110870；2. 天津电气科学研究院有限公司，天津市 河东区 300450）

0 引言

目前，海上风力发电机组朝着单机功率10 MW级发展，风电机组模块化设计成为主流[1-3]。随着风电机组功率需求提高，风电行业应用较少的中压六相永磁同步发电机(medium voltage sixphase permanent magnet synchronous generator，MVSPMSG)在风电行业前景逐渐明显。由于MVSPMSG 多一套绕组，控制灵活性、效率大幅提升[4]。同时，变流器容量也随之提高。中压变流系统具有的低电流、并网适应性好等优点[5-6]，是破解常规低压、大电流系统损耗大，开关器件电流应力大等问题的关键。目前，市场应用的中压变流拓扑有二极管中点箝位型(neutral point clamped，NPC)、飞跨电容型及主动箝位型3种[7]。二极管中点箝位型变流器结构复杂性适中、并网适应性良好[8]，故选用此拓扑结构为中压三电平变流器结构方案。

为使MVSPMSG 以最大功率输出，需要变流器控制风机，实现风能最大捕获和并网功率的稳定。现有研究重点主要集中在变流控制系统可靠性提升、谐波电流抑制、损耗分析等方面。文献[9]中NPC 变流系统采用断续空间矢量脉宽调制(space vector pulse width modulation，SVPWM)控制提高系统载波频率，降低开关损耗，但在MVSPMSG控制中的应用有待研究。文献[10-11]中分别提出三维SVPWM和分类SVPWM算法来降低传统SVPWM计算复杂性。然而，上述研究多针对机、网侧变流器单独控制，缺少风速波动对机侧变流器控制稳定性的影响。因此，在波动风速下为使MVSPMSG 能够以最大功率输出，本文将最大功率跟踪策略应用到NPC 变流器控制。同时，NPC变流器存在直流中点电位失衡问题。与现有增加额外器件均压方案相比，以SVPWM 方法为基础的中点均压控制方案更适用[12-13]。文献[14]提出基于零序分量的载波调制方法，用来减小电容压差，降低并网电流的谐波成分。文献[15]采用虚拟空间矢量脉宽调制(virtual space vector pulse width modulation，VSVPWM)算法来降低直流电压波动，但算法执行时间长、电压畸变严重。文献[16]提出基于小矢量作用时长的中点电位平衡调控策略，但存在一定的不可控区域。文献[17-19]则依据小矢量和中点电位间关系提出一种可变平衡系数的中点电位方法，但仍存在一定不可控区域，导致中点电位无法均衡。因此，本文提出融合调制系数与矢量组选择，用于消除中点电位不可控区域，提高中点电位平衡度。

综上所述，本文设计一种适用于MVSPMSG的最大功率跟踪方法，通过转矩及双d-q电流环的闭环组合实现MVSPMSG 最大功率捕获。同时，为平抑直流中点电位波动，采用调制因子和矢量组选择2种方案协调调控用于中点电位平衡控制。最后，通过仿真验证本文所提控制策略有效性，为大功率永磁同步电机(permanent magnet synchronous generator， PMSG) 控制提供理论参考。

1 中压三电平风电变流器控制策略

1.1 10 MW永磁风电机组变流系统结构

10 MW风电变流系统结构采用MVSPMSG搭配分布式NPC型变流方案，并网通道采用双5 MW变流器并联而成，拓扑结构如图1 所示。MVSPMSG为双Y接不共中性点定子绕组，2套定子绕组间以不对称分布30°排列。由于MVSPMSG定子绕组中不存在5、7次等低次谐波，故具有转矩脉动小、并网适应性好等优点。机、网侧变流器均采用NPC 型结构。机侧变流系统用于MVSPMSG 的转速及功率控制，网侧变流系统用于直流侧电压及并网控制。

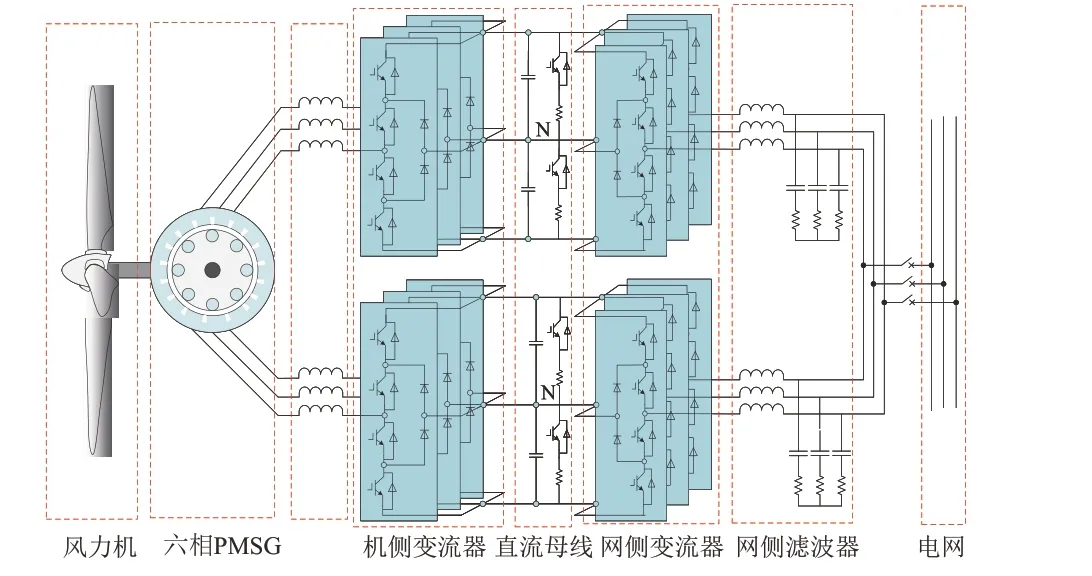
图1 10 MW永磁风力发电机组并网结构图Fig.1 Grid connection structure of 10MW PMSG

1.2 基于最佳转矩给定的MVSPMSG 最大功率跟踪控制策略

在最大功率跟踪方法方面，与转速控制、功率控制相比较，转矩控制只需要按照电机输入转矩和转速间所满足的最佳转矩曲线进行调控即可，故其具有调控方便、简单的优点。

为有效控制MVSPMSG，建立MVSPMSG 在双dq同步坐标轴下的电压及转矩方程，分别为

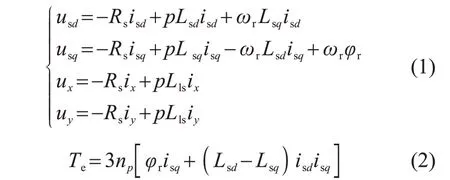
式中：usd、usq、isd、isq分别为表示电压、电流在dq旋转子平面的分量；ux、uy、ix、iy分别表示电压、电流在xy子平面内的分量；Lsd和Lsq分别为定子直轴、交轴电感；φr为永磁体励磁磁链；Rs为定子电阻；ωr为电角速度；np为极对数，其中下标p为分算子。

机侧变流器在采用id=0 的控制方式下，电磁转矩表达式为

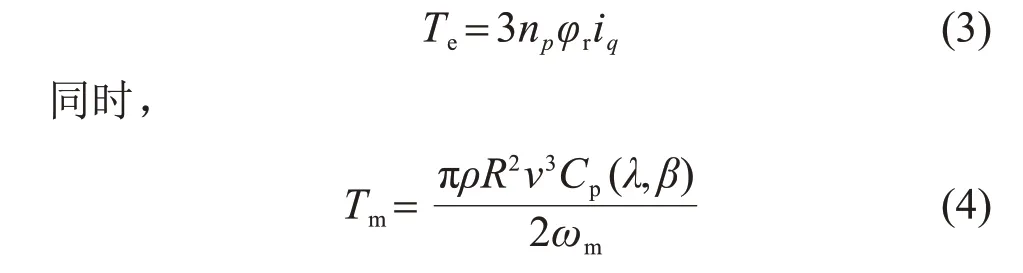
式中：R为叶轮半径；ρ为空气密度；λ为叶尖速比；β为桨距角；v为风速；Cp为风能利用系数；ωm为发电机角速度。

式中：kp、ki分别为电流内环的比例与积分系数；idref和iqref分别为dq坐标系下电流参考值。

由解耦控制可得出机侧变流器控制框图如图2所示。

图2 机侧变流器控制策略框图Fig.2 Control strategy block diagram of converter at generator side

根据式(6)计算q轴电流参考值，而将d轴电流给定值置零。dq轴电流给定值与电流采样值偏差经电流内环PI 计算，得到dq坐标系下的电压值，对其采取反Park变换后即可得到αβ坐标系下的电压值Uα、Uβ。最后将电压值输入三电平SVPWM进行调制，从而得出2 套变流器IGCT 的PWM脉冲信号。

1.3 基于电网电压定向矢量的网侧变流器控制

由网侧变流器调控对象特点可知，调控目标重点在于维持直母线电压恒定和最大有功功率并网。网侧变流器dq坐标系下数学模型可表示为式中：Rg、Lg分别为滤波器及线路等效电阻；SdX、SqX、SdZ、SqZ为dq坐标系变换参数，X和Z为开关变量，X表示桥臂上面2 个开关管导通，定义为1，Z表示下面2 个开关管导通，定义为-1；Ugd、Ugq为三相电压在dq坐标系的分量；igd、igq为三相网侧电流在dq坐标系的分量；ωg为电网工频电角度；Udc1、Udc2为直流侧上、下电容电压。

依据NPC型网侧变流器数学模型可知，变流器dq轴电压分量间存在耦合关系，同样需要采用补偿项对电压分量进行解耦输出，从而完成dq轴电压的独立控制。在进行解耦变换后，变流装置流向电网的有功功率P及无功功率Q分别为

由网侧变流器电压解耦后输出，可得其变流器调控方法如图3所示。

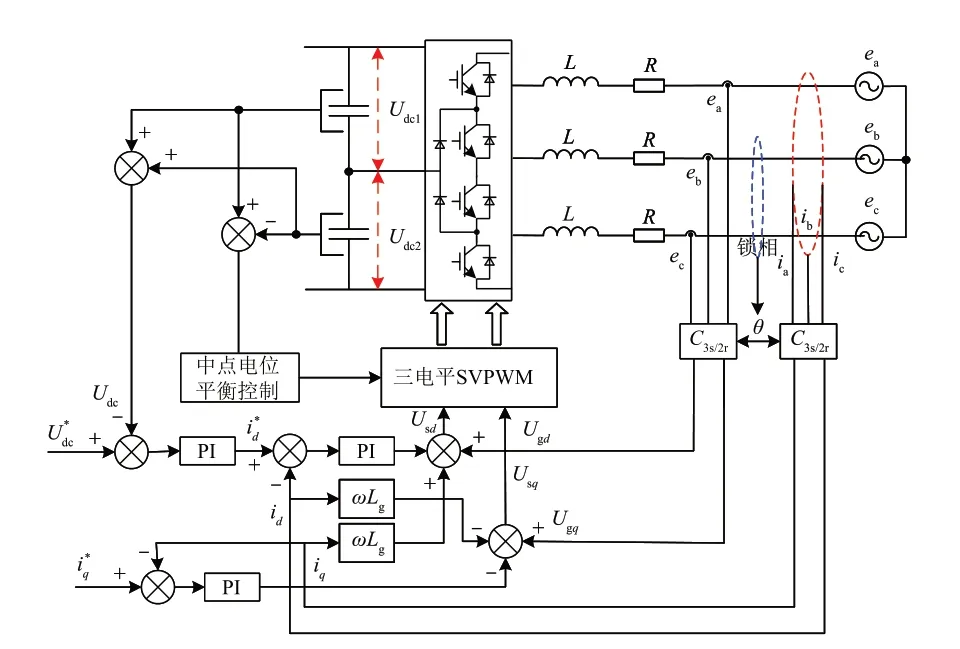
图3 NPC型三电平网侧变流器控制策略Fig.3 NPC three-level grid-side converter control strategy

2 直流中点电位平衡控制方法

2.1 基于SVPWM的直流中点电位调节机理

NPC型变流器中各相桥臂开关控制共需27个矢量，对于三电平SVPWM 而言，将27 个开关矢量分给为大、中、小(正小、负小)及零矢量，并依据所处空间位置、空间顺序编号及区域划分，具体情况如图4所示。

图4 不同开关状态坐标变换后的空间矢量图Fig.4 Space vector diagram after coordinate transformation in different switch states

由于不同矢量下变流器所处的工作状态存在差异，从而导致直流中点的电流流动存在差异，此时直流中点电位的失衡程度也大小不一。不同矢量状态下变流器开关等效模型如图5所示。

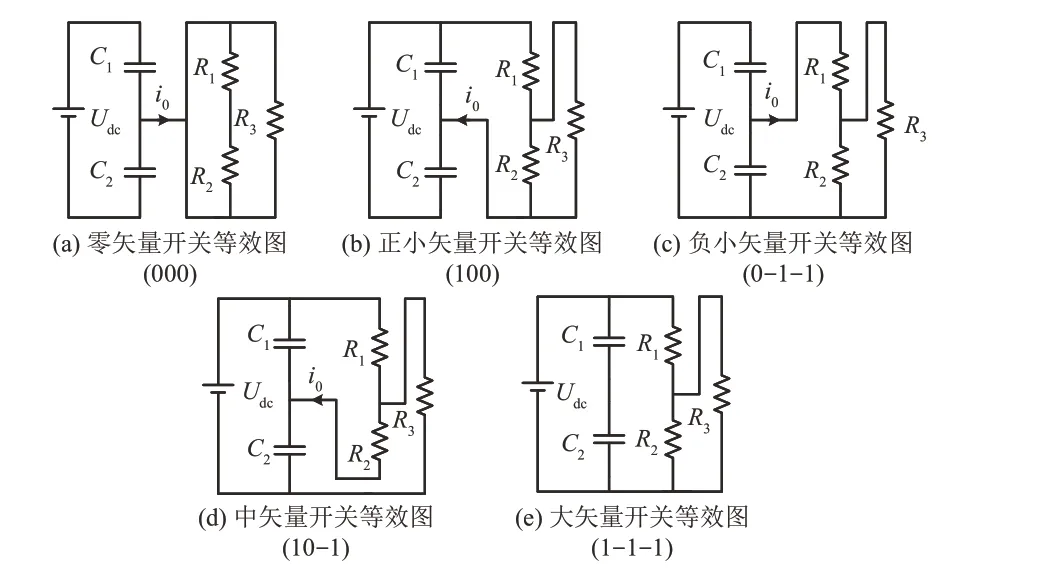
图5 空间矢量调制对中点电位影响Fig.5 Effect of SVPWM on neutral point potential

由图5 可知，在零矢量、大矢量作用下，直流中点不存在电流回路，因此直流中点电位无变化。在正小矢量及中矢量作用下，直流中点电流i0由负载侧流出，使得中点电位升高；在负小矢量作用下，直流中点电流i0由母线侧流出，致使直流中点电位降低。由直流中点电流的流动方向可以得出，正、负小矢量对直流中点电位影响互异，而中矢量则致使直流中点电位上升。因此，通过调整矢量组内正、负小矢量及中矢量的工作时间长度，从而完成对直流中点电位波动的调控。

2.2 基于调制系数与矢量组选择协调的中点电位平衡方法

变流器直流侧中点电位失衡主要由直流电容分压不均所引起，故直流侧中点处会存在剩余电荷。因此，可以将直流侧中点电位均衡控制转化为直流中点电荷量控制。由SVPWM 对直流中点电位调节规律可知，通过调整矢量组内中、小矢量工作时长，从而使直流电容中点在脉冲周期内的剩余电荷量一致，实现直流侧中点电位为0。

在一个开关周期内会存在一组基本矢量组，用于开关器件动作。而基本矢量组中通常存在4个矢量且至少含有一对正、负小矢量。在基本矢量组作用下，依据矢量作用顺序，将正小矢量、中矢量、大矢量及负小矢量作用下的直流中点电流分别定义为i00、i01、i02和i03，其中正、负小矢量作用下的中点电流流向相反。在一个开关周期T内，直流中点电荷剩余量ΔQ可表示为式中：Q1、Q2分别为上、下侧电容电荷量；C为电容值；T0、T1、T2分别为小、中、大矢量作用时间。

由式(11)可知，在ΔQ=0时直流中点电位可实现均衡调控。因此，本文引入时间调制系数α，将各个矢量作用下的SVPWM 脉冲时间划分为：(1+α)T0/4、T1/2、T2/2、(1-α)T0/2、T2/2、T1/2、(1+α)T0/4，具体划分及作用方式如图6 所示。中点电荷变化量ΔQ可表示为

由于在正、负小矢量作用下直流中点电流流向相反，即i00=-i03，则式(12)可表示为

由于SVPWM 脉冲作用时间要保持正值，故要使得|α|≤1，即在α∈(1，+∞]时，将α取值为1；在α∈[-∞，-1)时将α取值为-1。通过调节α对SVPWM 矢量作用时间进行修正来抑制直流中点电位失衡量。图6为SVPWM矢量作用时间图。

图6 SVPWM矢量作用时间图Fig.6 SVPWM vector action time chart

在通过调制系数α对直流中点电位调节过程中，调制系数α的取值范围被限制在[-1，1]。因此，在式(14)中，当分母T0i00→0，分子CΔUdc+T1i01+T2i02≠0 时，将导致α取值越限。而此时将α取值为-1 或者1 时，在一个开关周期内中点电荷无法全部抵消，故直流中点处仍具有较大电位波动。

由图4可知，某一开关矢量通常具备2组基本矢量方案，如I扇区1号区内矢量的合成组分为100、000、00-1、0-1-1 和110、100、000、00-1 两组，在其分别工作情况下，中点电荷增量ΔQ1、ΔQ2为

由式(15)可知，不同矢量组合下直流中点电荷增量ΔQ1、ΔQ2取决于小矢量00-1及100作用时长及直流侧电流。故选取不同基本矢量组所对应不同中点电流，直流中点处电荷量Q1、Q2为

在直流中点处，电荷量波动越小，则对电位的影响越小。因此，对直流中点电荷量|Q1|、|Q2|进行比较并取较小值，将其对应基本矢量组作为合成矢量。具体直流中点电位控制框图如图7所示。

图7 直流中点电位控制方法Fig.7 DC midpoint potential control method

3 控制策略仿真验证及分析

3.1 系统参数

为验证本文所提基于MVSPMSG 结构的最大风能跟踪控制策略以及直流中点电位调控策略有效性及准确性，在MATLAB/Simulink 仿真软件中搭建相应的物理仿真模型，具体模拟参数如表1 所示。

表1 10 MW MVSPMSG及变流系统参数Tab.1 Parameter of 10 MW PMVSPMSG and converter system

3.2 中点电位均衡调控策略仿真分析

本文分别对未采用中点电位调控方法、采用基于调制系数的中点电位调控方法以及采用调制系数与矢量组选择协调的中点电位调控方法时中点电位平衡情况进行仿真验证，结果如图8 和9所示。

图8 是否加入平衡控制时中点电位变化情况Fig.8 Midpoint potential changes with or without equilibrium control

图9 加入矢量选择时中点电位变化Fig.9 Midpoint potential changes when adding vector selection

由图8、9可知，当调制度为0.8，未采用中点调控方法时，直流中点电压在-220～280 V间脉动；采用基于调制系数的中点电位调控方法后，直流中点电压脉动范围降低至-75～45 V。而采用调制系数与矢量组选择协调的中点电位调控方法后中点电位波动范围进一步降低为-30～30 V，降低幅度高达50%，网侧变流器滤波前线电压波形为额定输出电压3 300 V，且电压波形得到改善，如图10所示。

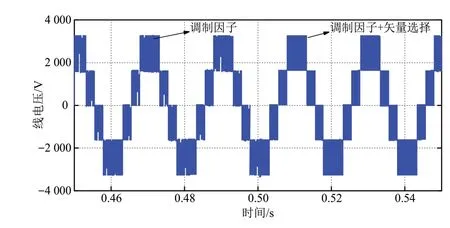
图10 加入矢量选择时线电压变化Fig.10 Line voltage curve when adding vector selection

3.3 10 MW SPMSG系统仿真分析

对10 MW 基于MVSPMSG的最大风能跟踪控制策略进行仿真分析。风速设置为渐变风，0～0.6 s内风速稳定在8 m/s，0.6～1 s增大至额定风速10.5 m/s，并在接下来的0.6 s 内保持不变，1.6 s后骤减至9 m/s直到结束。

MVSPMSG的dq轴电流波形如图11所示。当风速骤降时，由于绕组磁链矢量存在负向分量，使得发电机d轴电流出现暂时脉动，但很快又趋于零值电流。而MVSPMSGq轴电流仅与转矩有关，额定风速下定子q轴电流为峰值电流1 250 A，且2 组定子绕组dq轴电流相等。因此，只需要通过调节dq轴电压相等，从而完成MVSPMSG功率的平均分配。

图11 MVSPMSG的dq轴电流波形Fig.11 dq-axis current waveform of MVSPMSG

MVSPMSG定子绕组电流如图12所示，定子绕组的电流大小和波动频率都随着输入风速改变，额定风速下定子电流为额定值880 A，且2组绕组间的同相电流相位差为30°。

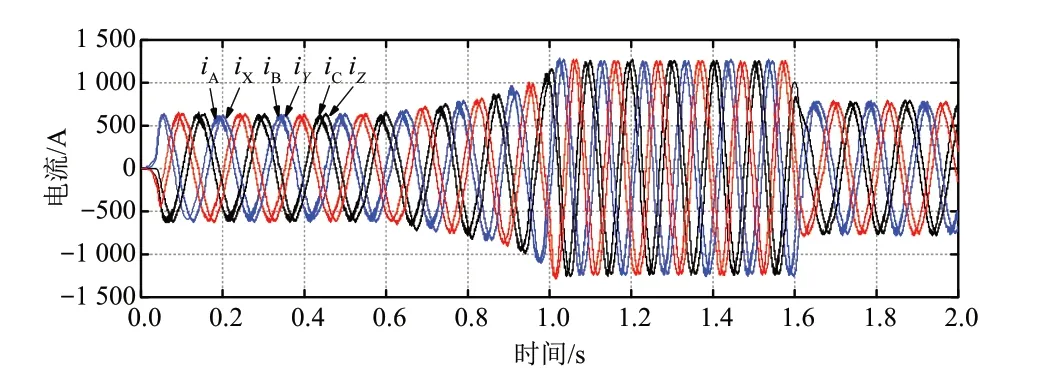
图12 MVSPMSG定子绕组电流Fig.12 MVSPMSG stator winding current

MVSPMSG 系统直流母线电压如图13 所示，2 组变流器母线电压稳态值相同，均为设定值5 000 V 左右。风速突变情况下，2 套直流母线电压均短时小幅波动后迅速恢复设定值，且波动幅值及波动时长相一致。

图13 双变流器直流母线电压Fig.13 DC bus voltage of double converter

网侧变流器的并网电压、电流及功率等曲线如图14、15 所示。并网相电压保持额定输出电压，而相电流则跟随输入风速而改变，电流输出波形较好，经FFT 计算，相电流谐波畸变率为2.47%，可以满足设计要求。网侧变流器的并网电压及电流波动方向相同，经滤波器补偿后系统功率由变流器流向电网。同时，并网有功功率跟随输出电流改变，额定风速下2 组变流器并网有功功率达到10 MW，系统功率因数接近1。

图14 网侧变流器并网电压、电流Fig.14 Grid-side converter grid-connected voltage and current

图15 单个网侧变流器输出功率Fig.15 Output power of a single grid-side converter

4 结论

研究基于MVSPMSG 的风电系统机侧、网侧变流器及直流侧控制策略，得出如下结论：

1）设计了适用于MVSPMSG 搭配NPC 型变流器的机侧变流系统最大功率跟踪控制策略，系统在变输入工况下仿真分析可得，变流器功率输出可动态跟随风速变化，额定风速下系统输出功率达到10 MW，满足系统要求且具有良好最佳风能跟踪性能。

2）分析NPC型变流器直流中点电位平衡调控方法，提出调制系数与矢量组选择协调中点电位调控策略，与单纯采用调制系数调控方法相比，所提方法可将中点电位波动范围降低50%左右。