基于空间六点不变量的道路立体目标识别方法*
张雅茜 韩 斌
(江苏科技大学计算机学院 镇江 212003)
1 引言
识别三维物体一直以来都是计算机视觉研究[1]的重要内容,然而由于摄像机成像[2]质量、光照、拍摄角度等因素影响,同一个物体在图像中的表征会发生巨大的变化。研究表明,几何不变量[3~5]可以消除因上述因素导致物体难以识别甚至无法识别的问题,并且其识别方法简单高效。
点和直线是描述物体外观的重要元素,描述提取图片上的特征点如角点[6]等兴趣点可以用于特征描述[7~10],基于这些点计算交比[11]等几何不变量,该方法受到广泛的关注与推广。罗钟铉[12]提出了基于特征数的一种新的形状匹配方法,利用物体的五点或者六点,根据射影不变量中共面五点的射影不变量计算公式[13],能够确定是否属于一个平面。
现实情况下,很多点并不满足共面条件,该方法有很大的局限性,因此本文提出从物体的空间点,提取物体的不变量,该方法不依赖所有点元素都在一个平面上,比共面五点的计算方法更加灵活方便。
2 算法流程
首先对图像进行预处理,主要包括灰度处理[14]及高斯滤波[15]等。为了提升射影几何量的计算精度和便捷性,采用ORB 描述子[13]作为特征点检测目标,然后对多幅图像的特征点进行匹配,获得匹配点对,为基于射影不变形的道路目标识别提供匹配特征点。
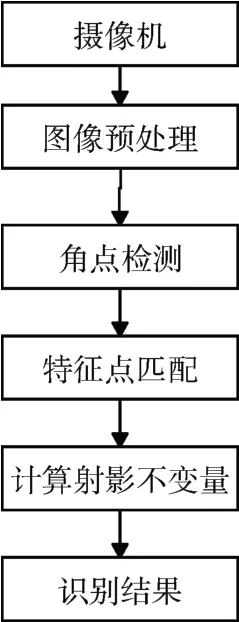
图1 系统技术路线
3 基于空间点元素的几何量计算方法
我们可将2D 不变量变换求解的思想运用到3D 不变量中,即寻找一种有效途径将复杂的空间构成关系简单化,把三点确定一平面、直线平面必交一点和两平面必交一线皆转化成共面关系下元素的不同组合形式。把空间元素的共点和共线用具有物理意义的量来表示,即引入实元素和虚元素[16]。这两个量无法割裂使用,需要结合互补,通过合理搭建把空间元素巧妙转化为共面关系。
假设存在α和β两个平面,并且α平面存在三个点A,B,C,β平面存在三个点D,G,H。其中平面α和β的相邻边为DE,如图2所示。
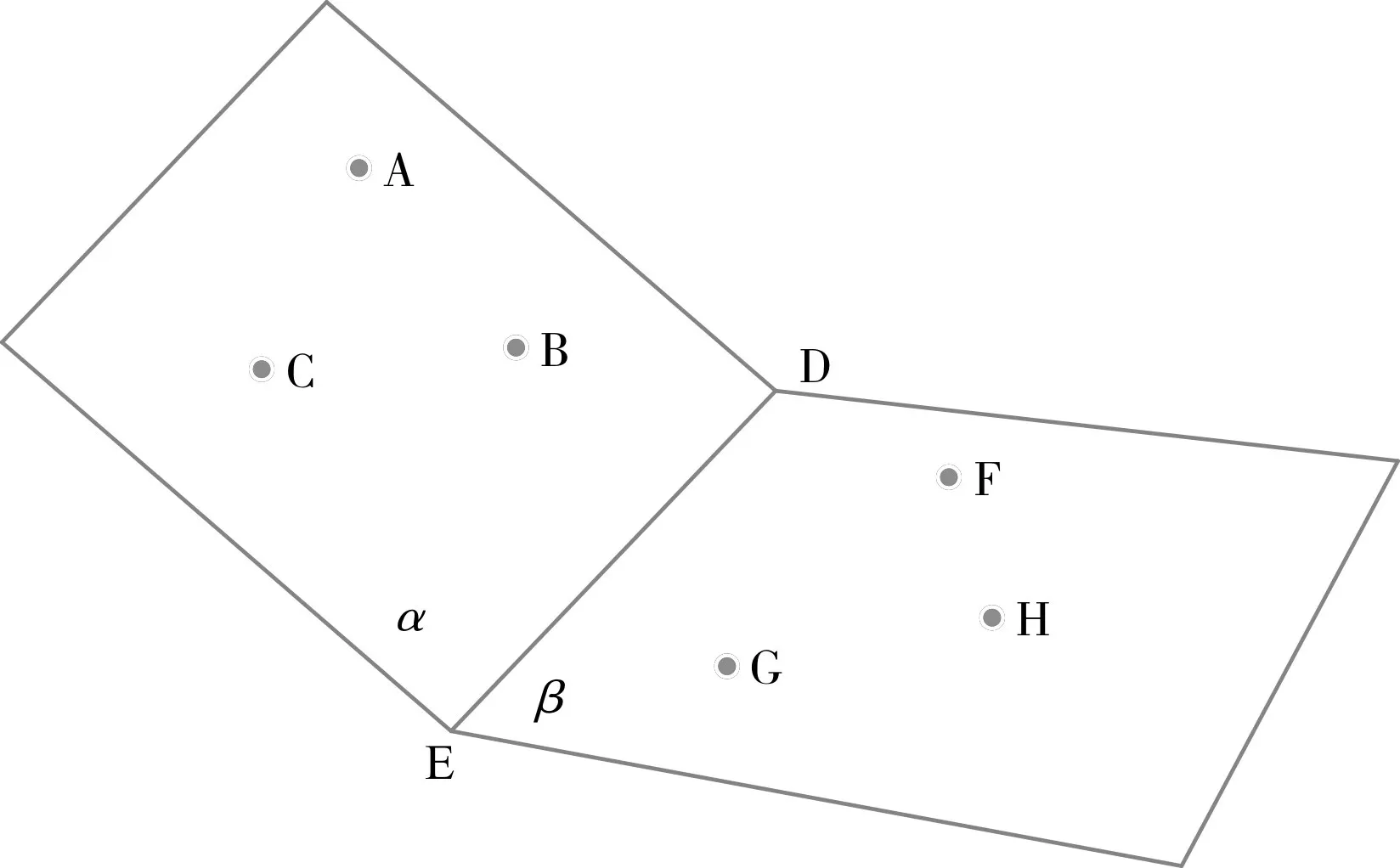
图2 空间两个平面示意
根据摄像机射影变换公式[17~18],α平面上存在如下公式。
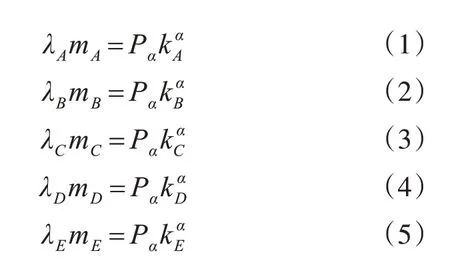
将A、B、C、D、E 分别组成多组三个点矩阵形式,得到:


从上式可以知道,该几何不变量只依赖点的空间坐标,与投影视角[19]、摄像机参数[20]等无关。因此对于区分物体的空间结构具有很大的参考意义。
4 实验结果与分析
4.1 模拟实验
本次实验采用的硬件包括:个人电脑主机,处理器Intel i3,主频2.8GHz,内存8.00GB。软件包括:Windows 10,三维造型软件SolidWorks 2016 ×64 Edition,Microsoft Visual Studio 2015,OpenCV 3.4等。
为了验证上述空间点元素射影不变量的计算方法,采用SolidWorks 三维造型软件绘制如下空间相邻平面结构体。如图3,在两个平面上分别预先设置点A、B、C、D、E、F、G、H,为了验证空间点元素的几何不变量的正确性,分别设置两个平面的夹角分别为10、20、30、40,分别截取不同视角的结构体的2D 图片。为了模拟3D 物体投射到相机平面的真实场景,对其2D 图片上各点图像坐标进行噪声处理[21~22],噪声强度分别为0.1,0.2,0.3。

图3 仿真3D结构体
表1 为实验记录,列向为不同的平面夹角,行向为不同强度的噪声值。从表中数据可以看出,即使噪声越来越大,图像越来越模糊,点的坐标发生了一定程度的偏移,其几何不变量仍然不会发生较大变化,说明空间点元素可以用于空间结构体的射影不变量计算。
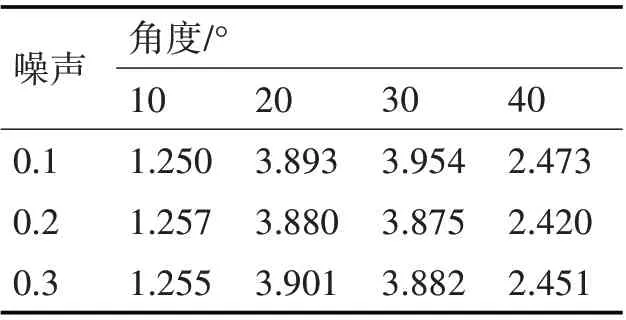
表1 不同噪声强度与不同夹角下结构体几何量
从不同角度拍摄结构体,得到不同角度下结构体的2D 图像。利用公式,得到该结构体的3D 不变量为11.279。
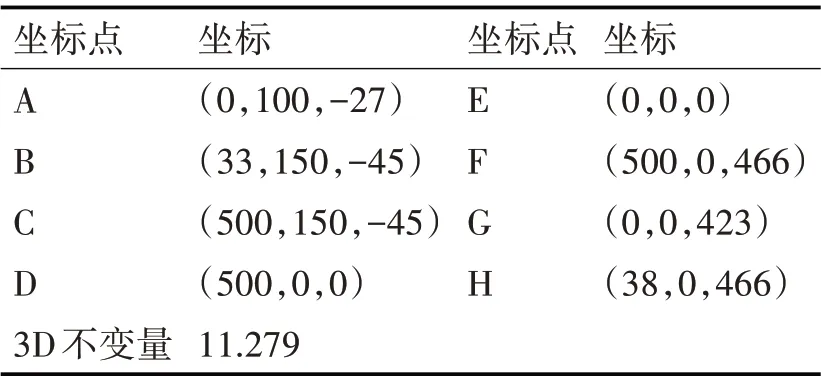
表2 结构体的坐标及3D不变量
为了验证结构在不同角度下图像上恢复的几何不变量的稳定性,从不同角度和缩放程度获得了物体的2D图像。


图4 结构体在不同角度下的2D图像
根据图中的2D 图像分别计算几何不变量。如表3所示,可以看到10张图像均可得到近似的几何不变量,与3D 几何不变量误差率均在一定的范围内。
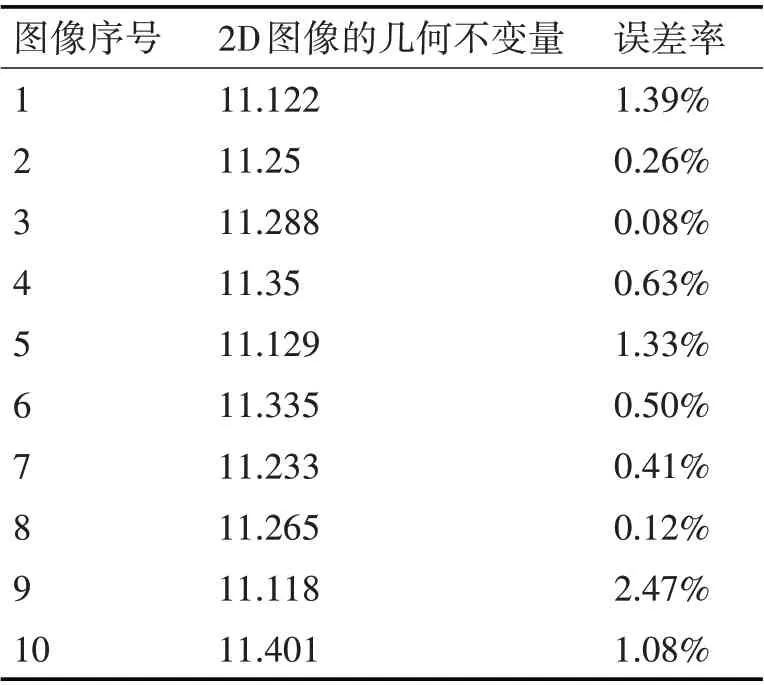
表3 各角度图像的几何不变量及误差率
4.2 实测实验

图5 关键点匹配关系


图6 更多视角的模型展示
利用空间点元素的几何不变量,分别计算人行道和红色立方体的2D 图像中的几何量,计算结果如表4 所示。可以看到立方体的几何量标准偏差较小,而人行道的几何量标准偏差较大,因此可以得到人行道不满足基于空间六点不变量理论,该人行道是一个具有虚拟3D效果的平面图案。

表4 不同视角下的交比及标准差
5 结语
本文针对道路上的目标属于虚拟3D 图案还是真实物体,提出从物体的空间点,提取物体的不变量,该方法不依赖所有点元素都在一个平面上,比共面五点的计算方法更加灵活方便。为了验证提出的空间点元素几何不变量计算方法的有效性,采取实施模拟实验进行验证,实验结果表明不同角度下同一物体的几何不变量具有唯一性,并且在不同的噪声强度下均具有一定的鲁棒性。

