改善区域间振荡阻尼的快速功率调制策略研究
古庭赟,杨骐嘉,徐梅梅,肖小兵,伍华伟,吴贵烘,李宇骏
(1.贵州电网有限责任公司电力科学研究院,贵州 贵阳 550002;2.西安交通大学电气工程学院,陕西 西安 710049;3.贵州电网有限责任公司都匀供电局,贵州 都匀 558000)
0 引言
随着风电渗透率的不断增大,风电的接入方式已从原来的小容量、分布式的接入向大规模、集中式的接入转变[1-5]。因此,高占比风能下系统稳定性需要进一步的研究。文献[6]最早开展了基于定速感应风机接入下的系统稳定性研究。研究表明,风力机组占比的不断增大可有效改善系统的阻尼特性。文献[7]通过特征根求取和分析振荡模态,分析了高占比风力机组对系统阻尼的影响,验证了一定比例的风力机组可有效改善系统阻尼。文献[8]提出了暂态分析下DFIG 的降阶模型。文献[9]求取了系统的特征值和阻尼比,分析了在不同风能占比下,风能占比变化对电力系统稳定性的影响并不呈现单一性质,其作用机理并不明晰。
当系统中风能占比较大,其对电力系统的动态影响不可忽略[10-13]。因此研究风力机组的阻尼控制器对提高电力系统稳定性有着重要意义。目前,风力机组主要通过在有功功率环和无功功率环中加入阻尼抑制器来抑制系统的低频振荡问题[14-15]。文献[16]提出了在风力机组有功功率环上加附加阻尼控制器的设计思路,其基本思路是当系统发生振荡时,通过改变风力机组的有功功率出力来增加系统阻尼。文献[17-18]通过采用粒子群算法(Particle Swarm Optimization,PSO)来优化风力机组电力系统稳定器(Power System Stabilizer,PSS)的参数,进而改善系统的稳定性。文献[19-20]通过在风力机组无功功率控制环加入阻尼控制器,增大系统阻尼。
近年来,随着非线性控制技术的不断发展,大量基于非线性控制手段来抑制风力机组低频振荡的技术应用于风机控制当中。文献[21]采用滑模控制通过调制风力机组的暂态有功出力来抑制电网的低频振荡。文献[22]采用模型预测控制方法,基于暂态过程中同步电机功率振荡最小的控制来提升系统阻尼。文献[23]采用自适应控制方式依据风机运行状态不断调整阻尼控制的系数,抑制系统的低频振荡,增大系统阻尼。然而文献[24-25]中方法均需要大量的计算以及依赖于广域测量系统,可靠性差。
前人在风力机组抑制电网低频振荡方面做了大量的探索工作,但大多基于广域测量系统,可靠性较差,并且缺乏详细的风力机组模型对系统动态特性的影响研究。因此,本文在详细考察风机动态模型的基础上,提出一种通过风机快速功率调制来改善区域间振荡阻尼的方法。该方法在传统风机双闭环控制结构上,选择邻近的发电机角速度的增量Δω作为阻尼控制的输入信号,将双馈式感应风力机组(Double-fed Induction Generator,DFIG)转子功率的增量ΔP作为输出信号加在双馈风机有功功率控制环上,有效改善了系统的阻尼,提升了系统的动态行为。
1 DFIG数学模型
本文所研究的DFIG 单机无穷大系统如图1 所示。图1 中LS 表示齿轮箱的低速部分,HS 示齿轮箱的高速部分。DFIG 将风轮机输出的机械功率Pt转化为电功率,DFIG 在正常运行状态下有风机超同步运行和次同步运行两种不同的运行模式。因此,基于双馈风机灵活多变的运行模式,DFIG 非常适合随机风速下的场景。
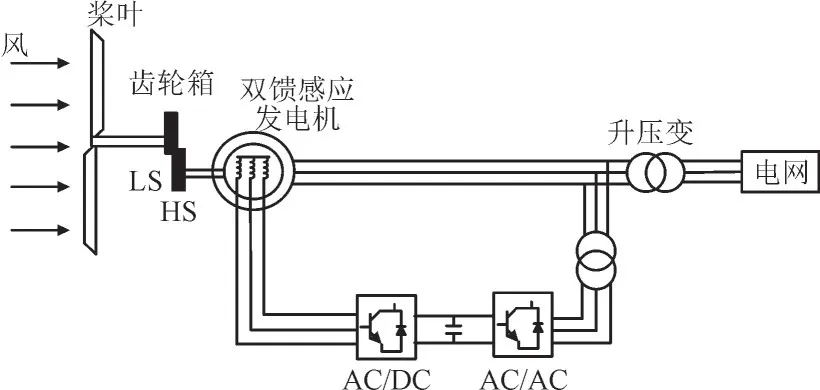
图1 DFIG单机无穷大系统Fig.1 Single machine infinite bus system of DFIG
1.1 风轮机模型
风轮机的工作机理为风吹动桨叶,桨叶经过齿轮箱将机械能传递到双馈感应发电机。风轮机获取的机械功率Pt如式(1)所示:

式中:Cp为风能利用系数;ρ为空气密度;A为扫风面积;vwind为风速。
本文DFIG 采用最大功率追踪(Maximum Power Point Tracing,MPPT)的方式去捕获最大的机械功率。
1.2 传动系统
在分析DFIG 风能转换系统的小干扰稳定性时通常采用多质量块模型表征其能量传递的轴系,数学模型可由式(2)—式(4)表达:
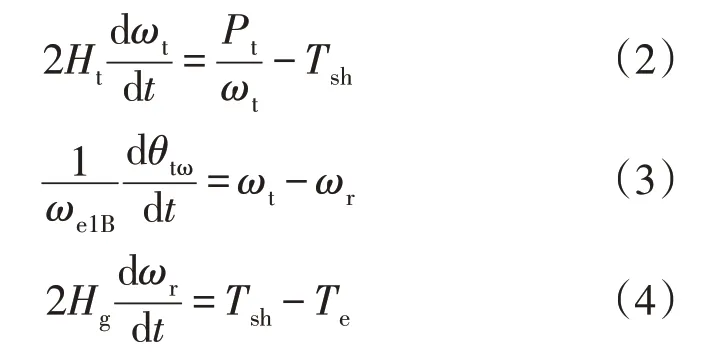
式中:Tsh为轴系转矩;Te为发电机电气转矩;Ht为齿轮箱的低速部分惯性时间常数;Hg为齿轮箱的高速部分惯性时间常数;ωt为风轮机转速;ωr为DFIG 转子转速;ωe1B为同步转速;θtω为2 个质量块的电角度差。
在进行区域间阻尼振荡研究中,一般认为风力机功率暂态波动不大,转子转速的变化范围较小,风力机组原动机在暂态过程中保持恒定,为一常数。文中所有的电气量均采用标幺值表征。即:
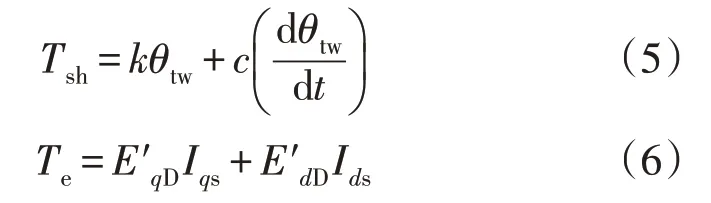
式中:k和c分别为轴系刚度和阻尼系数;E′qD与E′dD分别为转子q轴和d轴的暂态电压;Iqs与Ids分别为定子q轴电流和d轴电流。
1.3 感应发电机模型
本文采用q轴领先d轴90°的dq坐标系。各暂态变量定义如式(7)—式(8):
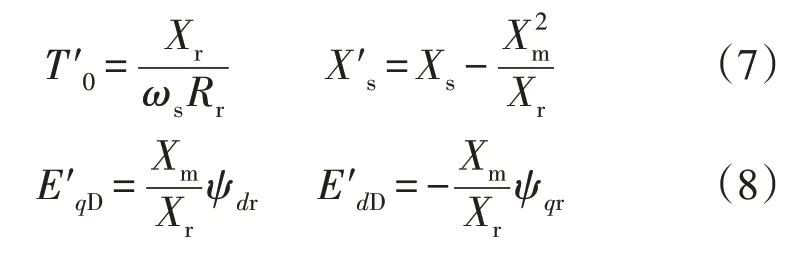
式中:T′0为暂态开路时间常数;ωs为系统同步转速;Rr为转子电阻;X′s为暂态电抗;Xm为定子与转子之间的互阻抗;ψdr为转子d轴的磁链;ψqr为转子q轴的磁链;Xs为定子电抗;Xr为转子电抗,
对于大型发电机,定子的动态变化过程会远远快于转子,因此定子磁链的变化过程可以被略去,只有转子磁链的变化过程需要被加以考察,采用此简化后的DFIG 的模型如式(9)—式(16):
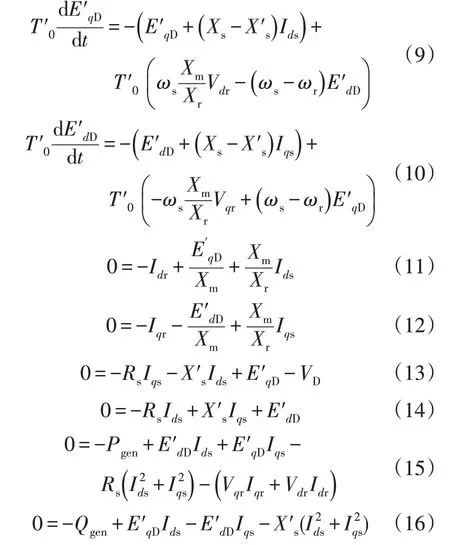
式中:Rs为定子的电阻;VD为风力机的机端电压;Pgen和Qgen分别为与电网交换的有功功率和无功功率;Idr为转子d轴电流;Iqr为转子q轴电流;Vdr为转子d轴电压;Vqr为转子q轴电压。
1.4 换流器模型
AC/DC/AC 转换器包括2 个脉冲宽度模块逆变器。定子侧换流器通常认为是理想换流器,其主要作用是传输转子侧经直流线路输送的有功功率;通常考虑转子侧换流器的动态过程即可。本文中,转子侧换流器采用d轴定子磁链定向,定子侧的电压Vqs=VD,Vds=0。
控制系统采用最常见的比例-积分(P-I)控制。外环一般控制风力机输出的有功和无功功率,而内环电流控制则控制换流器的输出电流。内环输出为转子侧换流器逆变dq轴电压。PQ解耦控制的框图如图2 所示,其中Pref和Qref分别为与电网交换的有功功率和无功功率的参考值,分别为转子dq轴的参考电流,s为微分算子。
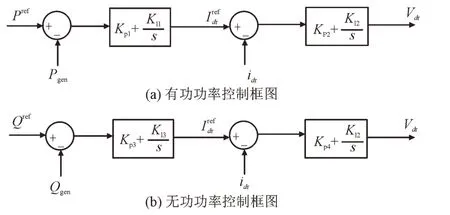
图2 转子侧dq解耦控制框图Fig.2 Rotor-side dq decoupling control
其数学方程表征如式(17)—式(22):
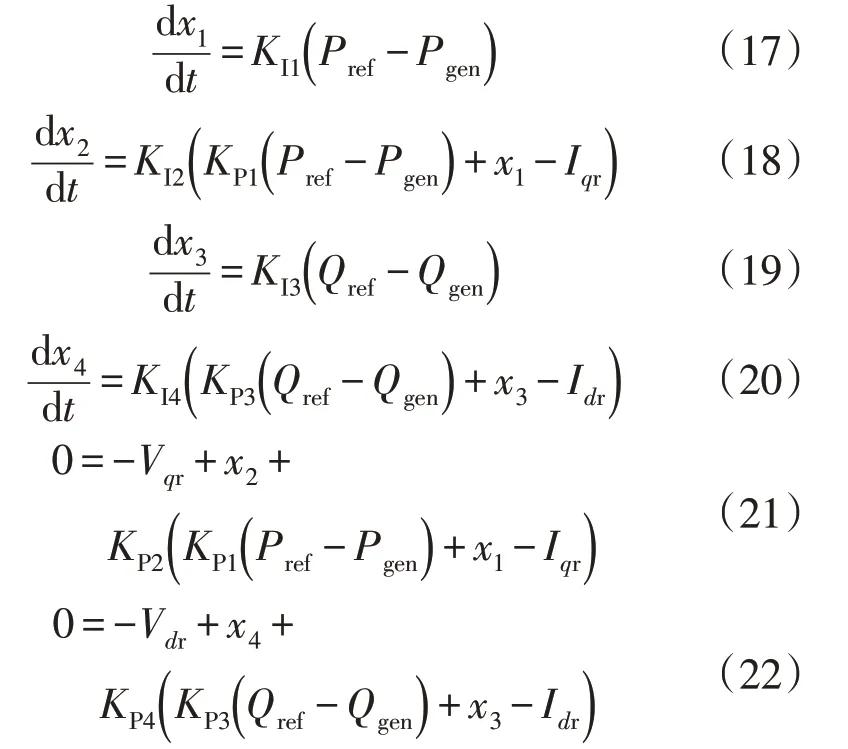
式中:x1为有功外环控制积分状态量;KI1为有功外环控制积分系数;KP1为有功外环控制比例系数;x2为电流内环控制积分状态量;KI2为电流内环控制积分系数;KP2为电流内环控制比例系数;x3为无功外环控制积分状态量;KI3为无功外环控制积分系数;KP3为无功外环控制比例系数;x4为电流内环控制积分状态量;KI4为电流内环控制积分系数;KP4为电流内环控制比例系数。
2 风力机组附加阻尼控制器设计
当系统在某一运行方式下,系统阻尼较小,极易发生低频振荡。为了提高系统的阻尼可在传统的励磁电压控制环节中加装PSS,通过改变励磁电压的参考值,增大系统主导特征根的阻尼比。利用自身相位的超前补偿作用,在一定程度上改善系统的阻尼水平,抑制低频振荡的发生。
PSS 作为一种附加励磁电压控制,其对电力系统小干扰稳定性的改善具有重要作用。到目前为止,由于PSS 的结构简单、控制代价较小、提升性能较佳,为改善系统阻尼抑制振荡的较佳措施。
与传统同步发电机组PSS 设计类似,风力机组的附加阻尼控制器的设计框图如图3 所示,其中V1,V2分别代表中间过程状态变量,Pref为DFIG 有功参考值,Popt为最大功率跟踪值,TR为信号测量环节时间常数,T0为隔直环节时间常数,T1和T2为超前滞后相位补偿环节时间常数。
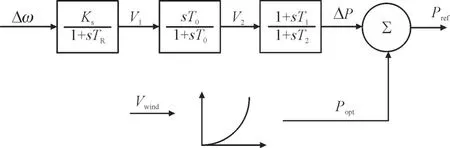
图3 附加阻尼控制器的设计框图Fig.3 Design process of DFIG damping controller
本文将某发电机功角(某主导特征根的参与因子较高的主导发电机组)角速度的增量Δω作为输入信号,将DFIG 转子功率的增量ΔP作为输出信号。
在风力机组装设附加阻尼控制器,可以充分利用风机功率控制的快速性。在系统发生频振荡时,快速调整风机输入网络的有功功率,从而对低频振荡产生抑制作用。
由图3 可知,与传统同步发电机组PSS 类同,DFIG 的附加阻尼控制器包含3 个基本模块:信号测量环节,隔直环节和超前滞后相位补偿环节。附加阻尼控制器的输出信号表征在系统发生低频振荡下风机转子功率的增量ΔP。
在DFIG 上装设附加阻尼控制器后,DFIG 有功参考值Pref可表征为最大功率跟踪值Popt加上附加阻尼控制器有功功率变化量记为ΔP,具体可表示为:

因此,风机有功功率参考值可表示为:
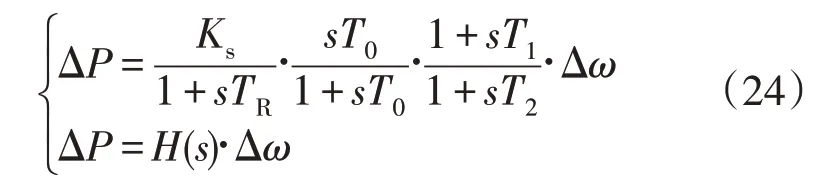
式中:H(s)为Δω与ΔP之间的控制传递函数。
系统控制框图如图4 所示。

图4 系统的控制框图Fig.4 Control block diagram for system
整个系统的闭环传递函数可表示为:
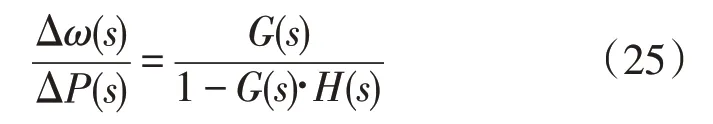
式中:G(s)为Pref与Δω之间的传递函数。
假设所配置的闭环极点为sd,那么传递函数的幅值和相角需要满足式(26):

式中:arg(·)为传递函数的相角;|·|为传递函数的幅值。
3 模态分析
任意电力系统的数学模型可表示为:

式中:x为状态变量;y为代数变量
依据李雅普诺夫稳定性第一定律,一般将式和式所描述的动态系统在某一稳定运行点(x0,y0)处进行Taylor 展开,保留系统一次项,得到非线性动力学系统在平衡点领域附近的近似线性模型。所得系统的线性模型的状态空间方程可表示为:
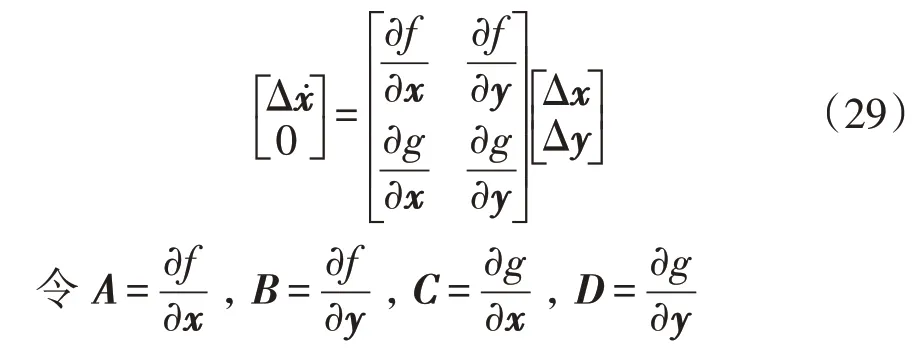
则状态空间方程可表示为:
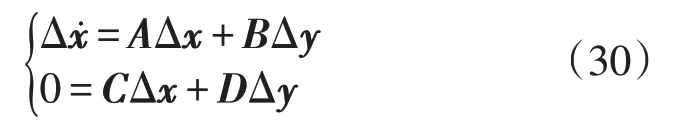
消去代数变量Δy,得到:
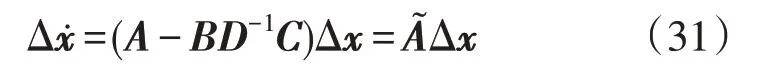
相比代数变量,本文更为关心状态变量的变化。在加入DFIG 后,系统增加的状态变量主要是风轮机相关状态变量xt=[ωt,θtω,ωr],双馈发电机状态变量xg=[E′dD,E′qD],换流器状态变量xc=[x1,x2,x3,x4]。当双馈风机上继续装设附加阻尼控制器时,会相应引入附加阻尼控制器相关状态变量xD=[V1,V2,ΔP]。
4 算例分析
4.1 系统描述
本文在电力系统电磁机电暂态混合仿真程序(DIgSILENT/PowerFactory)中搭建了用于系统低频振荡分析的2 区域4 机系统,如图5 所示。其中数字代表节点编号,L7 和L9 为负荷,Pac为2 区域间的传输功率。左侧发电机G1 与G2 构成区域1,右侧发电机G3 与G4 构成区域2。4 台发电机均采取7 阶模型,并配有相应的励磁调节系统。由于励磁调节系统的暂态增益系数过大,该系统共有2 个区域内振荡模态及1 个区域间的振荡模态。本文主要关注区域间振荡模态的变化。

图5 含风场的4机2区域系统Fig.5 4-generator 2-area system with wind farms
本文在母线6 处将150 台2 MW DFIG 组成的风场通过1 个并网变压器接入4 机2 区域系统,同时减少区域1 的发电机G2 的有功功率输出,以确保母线6 流入电网的功率保持不变。
通过分析有无接入风场时系统的稳定性,来判断风机出力对系统区域间低频振荡的影响。图6给出了DFIG 接入风场后主导特征值(区域间振荡模态)的变化。

图6 有无DFIG接入的系统主要模式特征值Fig.6 Key eigenvalue with and without DFIG
图6 中特征值由-0.144 01±j3.106 44 变为-0.149 3±j3.210 29,阻尼比因此从4.63%增加到4.65%,变化较小。
4.2 特征值分析
本文对该系统有无接入DFIG 阻尼控制器两种情况分别进行小干扰稳定性分析,图7 反映了两种情况下该系统主要模态的特征值变化。
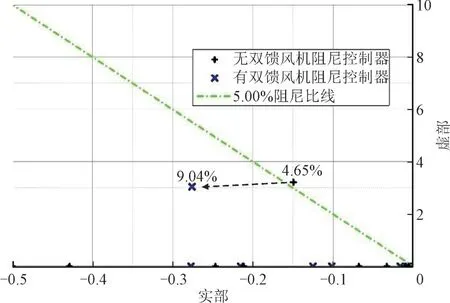
图7 两种情况下主要模态特征值Fig.7 Key eigenvalue with and without DFIG damping controller
由图7 可知,在接入双馈风机阻尼控制器后,反应系统主要模态的特征根向左移动,这表明系统阻尼得到了改善,振荡衰减速度变大。主导特征值由-0.149 3±j3.210 29 变为-0.275 76±j3.051 71,特征值虚部的变化不大,其振荡频率从0.511 1 Hz略微降低到0.4837Hz。特征值实部得到变化较大,从-0.149 3 变为-0.275 76,阻尼比因此从4.65%增加到9.04%。特征值计算分析结果表明,在加装了DFIG 阻尼控制器后,系统的阻尼得到了明显的改善,系统受到干扰后其电气量振荡将会以较快的速率衰减。
4.3 仿真分析
本文在DIgSILENT/PowerFactory 中开展暂态数值仿真计算分析。如图5 所示,t=30 s 时,在母线8处接入三相金属性接地故障,300 ms 后故障切除。典型的4 机2 区域系统参数可参考文献[25]。2 MW双馈风机参数如表1 所示。

表1 2 MW双馈风机仿真参数Table 1 Simulation parameters of 2 MW DFIG
当DFIG 装设了阻尼抑制器后,DFIG 的有功出力会随着振荡的变化而变化,从而为系统提供阻尼。图8 给出了故障后有无阻尼抑制器两种情况下DFIG 出力随时间的变化。可以发现,当装设阻尼抑制器后,双馈风机的有功出力在其作用下发生明显的变化;阻尼抑制器的暂态增益参数(Ks)越大,有功出力的调整越为明显。
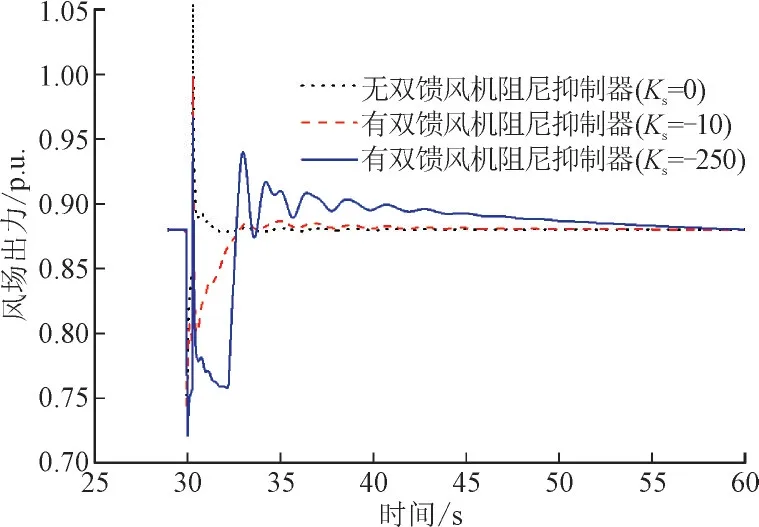
图8 有无阻尼抑制器DFIG出力随时间的变化Fig.8 Active power change with time of DFIG with and without DFIG damping controller
在限定的有功出力调整范围(ΔP为0.15 p.u.)内,阻尼抑制器均能为系统提供阻尼。图9 表示有无DFIG 阻尼抑制器时,发电机G1 与G3 的相对功角差随时间的变化曲线。
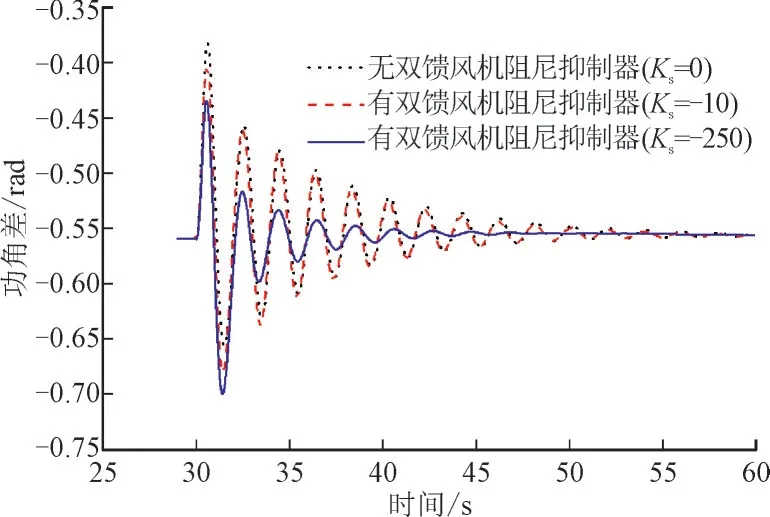
图9 有无阻尼抑制器功角差13随时间的变化Fig.9 Change with time in power angle with and without DFIG damping controller
图9 表明在双馈风机加装阻尼抑制器后,发电机G1 与G3 之间的相对功角差较不加装阻尼抑制器有明显的改善,振荡以较快的速度衰减,且暂态增益系数越大(在不超过有功出力调整范围的情况下),抑制效果更明显;当暂态增益系数较小时(Ks=-10),抑制效果不显著。
节点电压的变化同样验证了阻尼抑制器的附加阻尼作用。图10 给出了母线8 的电压随时间变化的曲线。很明显,在节点8 电压的变化趋势同发电机G1 和G3 之间的功角差的不变化趋势一致。
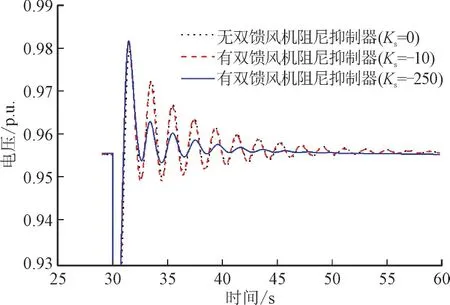
图10 有无阻尼抑制器母线8电压随时间的变化Fig.10 Voltage change with time of bus 8 with and without DFIG damping controller
由图8—图10 可以看出暂态实验仿真结果同小干扰特征值计算分析结果完全一致,表明在风力机组中加装阻尼抑制器,通过风力机组的快速功率调制,可以非常有效地提高系统关键模式的阻尼,从而改善系统的小干扰稳定性。
5 结语
随着以DFIG 为主的风力发电占电力系统容量比例的不断上升,DFIG 自身小干扰稳定性对系统稳定性的影响日益突出,风力机组附加阻尼控制器对提高电力系统稳定性的作用也日益明显。本文提出一种基于DFIG 的快速有功功率调制改善系统阻尼的方法。该方法在传统DFIG 双闭环控制结构上,选择发电机角速度的增量Δω作为阻尼控制的输入信号,将DFIG 转子功率的增量ΔP作为输出信号加在DFIG 有功功率控制环上。加装DFIG 附加阻尼控制器前后系统的小干扰分析结果和暂态时域仿真结果一致表明加装DFIG 阻尼控制器可有效改善系统的阻尼水平,抑制低频振荡的发生。
本文的重点在于采用本地信号抑制低频振荡,考察了风力机组的动态模型,并给出小干扰建模、稳定分析以及阻尼控制器设计的一般方法。控制性能(附加阻尼的效果)与控制代价(暂态增益系数及有功出力调整范围)之间的协调优化以及暂态增益系数与有功出力调整范围的协调配合则是未来继续开展的研究工作。

