新疆阜康水库鲫生长与资源特征研究
杨博文,祁 峰,韩 璇,邢君霞,韩军军,封永辉,谢春刚,陈 朋*,马燕武
1.新疆维吾尔自治区水产科学研究所,农业部西北地区渔业资源环境科学观测实验站,乌鲁木齐 830000;2.新疆农业广播电视学校,乌鲁木齐 830000
1 材料和方法
1.1 样本采集
2016年7月于新疆阜康水库采集本研究所用鲫样本,采集网具为挂网。网目为6cm。采集鲫鱼样本39尾,测量鱼体体质量(W)(精确度0.1g)与体长(SL)(精确度1mm),其鳞片作为年龄鉴定材料。在Leica MZ75体视解剖镜下进行年龄鉴定,在Leica DFC300FX数码拍照系统下进行鳞片拍照,采用FishBC3.0.1软件测量轮径。
为了确切记录其出生世代,采用元月1日为年龄递增日期。未形成年轮的个体记作0+组,已经形成1个新年轮的个体记作1+组,依次类推。
1.2 数据处理与分析
数据分析与图片处理采用Microsoft Excel 2003、SPSS13.0和FISATⅡ软件。
采用Keys公式拟合体长与体质量的关系,依据Pauly方法对其幂指数进行T检验。采用Dahl-Lea进行体长退算。利用von Bertalanffy生长方程拟合求得年龄与生长的关系。利用生长特征指数(Index of length growth performance)比较不同种群间生长特性的差异。使用FISATⅡ软件的Beverton and Holt plot模块和VPA模块分别估算死亡参数参考值及资源量。
2 结果
2.1 生长特征
2.1.1 体长和体质量的关系
以捕获鲫鱼实测体长与体质量的数据做图(图1),得到其关系式为:
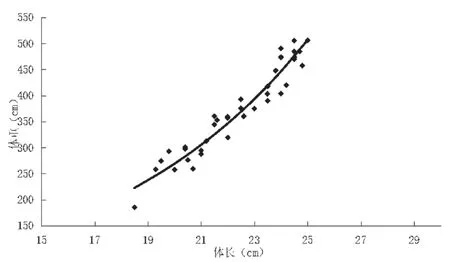
图1 阜康水库鲫体长与体质量的回归曲线Fig.1 Relationship between body length and weight of Carassius auratus in Fukang reservoir
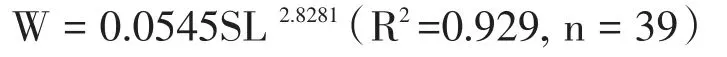
根据T检验显示,幂指数与3之间差异不显著(t=1.404<t0.0539=1.975),表明本研究中鲫的生长为等速生长类型。
b) 阀门打开瞬间管道内介质冲击阀芯,阀芯承受较大的侧向力,推动阀芯向套筒一侧靠近,如长期动作会导致阀芯导向环一侧磨损严重,引起导向环和套筒之间间隙增大,使得平衡密封环的一侧压缩量增大,从而导致磨损增大造成平衡密封环损坏。
2.1.2 生长退算
将已测量的轮径数值代入Dahl-Lea退算公式计算,求得各龄的退算体长和退算体质量(表2)。
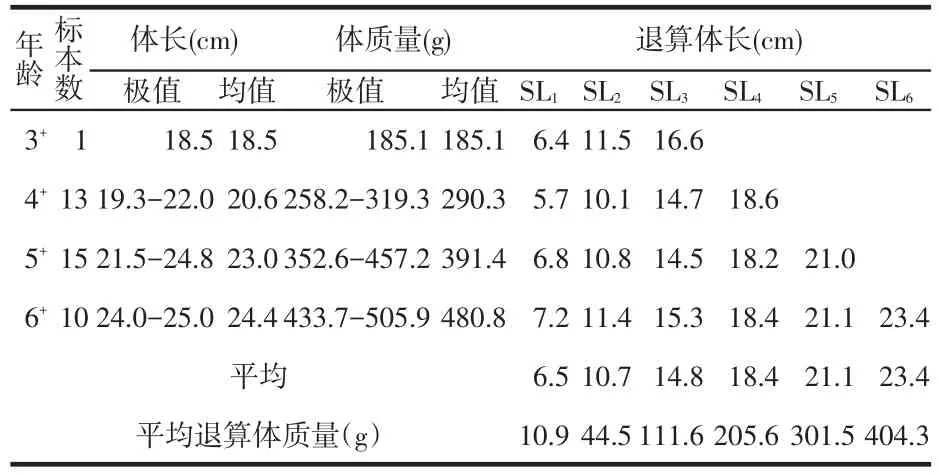
表2 阜康水库鲫各龄鱼退算体长和平均退算体质量Tab.1 Back-calculated body length(cm)at each age class and average back-calculated weight(kg)for Carassius auratus in Fukang reservoir
本研究使用网具网目较大,未能捕获小规格鲫,渔获物年龄组成为3~6龄,优势龄组为4~6龄,其中5龄组所占比例最大,为38.5%,其次为4龄组,占样本总数的33.3%,6龄组所占的比例为25.6%。
2.1.3 生长方程
根据Dahl-Lea法所得的退算体长平均值作Walford线图,显示Lt+1与Lt之间有显著的直线相关,满足von Bertalanffy生长方程条件。按最小二乘法拟合求得von Bertalanffy方程的各生长参数,得出鲫体长的生长方程:
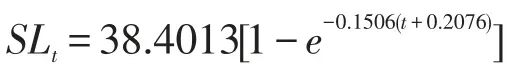
体质量生长参数根据各龄退算体质量数据进行拟合,得出鲫体质量的生长方程:
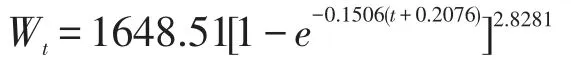
将鲫各龄的理论体长、体质量分别与各龄所实测的体长、体质量进行χ2检验,得χ2=3.224<χ20.05=9.488(p=0.939)和χ2=1.521<χ20.05=9.488(p=0.982),表明差异不显著,得出生长曲线拟合程度高。
2.1.4 生长速度
对鲫的vonBertalanffy方程求导变换,得到体长和体质量的生长速度(dL/dt,dW/dt)及加速度(d2L/dt2,d2W/dt2)的方程为:
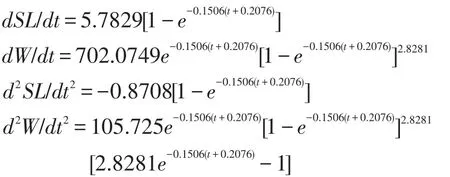
如图2所示,体长生长速度随着年龄的增加而逐渐下降,生长加速度却逐年上升,但生长增速均为为负值,说明体长生长速度(dL/dt)随着年龄的增加而递减。体质量生长速度曲线(dW/dt)是具有拐点的曲线,当体质量生长加速度为0时的年龄即生长拐点的年龄tIP,将von Bertalanffy生长方程式中的b、k和t0代入tIP=lnb/k+t0方程,得出鲫生长拐点年龄tip为6.7龄,此刻体长为TLi=24.87cm,体质量为Wi=478.7g。该年龄段与鲫体质量生长率曲线相吻合。表明该水库鲫在6.7龄前体质量的生长加速度为正值,但随着年龄的增长逐渐变小,最后变为负值,表明该体质量生长加速度随年龄的增长而递减。将von Bertalanffy生长方程中K、L∞数值代入生长特征指数方程中,得到该鲫的生长特征指数为:φ=5.40。
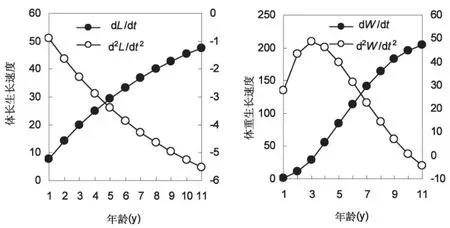
图2 阜康水库鲫体长、体质量生长速度与加速度曲线A为体长生长速度和加速度曲线,B为体质量生长速度和加速度曲线Fig.2 Growth rate,accelerated rate of body length and weight of Carassius auratus in Fukang reservoir A:Growth rate and accelerated rate of body length;B:Growth rate and accelerated rate of weight.
2.2 资源特征
2.2.1 种群生物量最大年龄
设鲫种群生物量为Bm,数量为Nt,平均个体体质量为Wt,则生物量B=Nt·Wt,随着年龄的增长,Nt不断减少,而Wt则不断增加,故Nt·Wt的函数极大值点即为最大生物量的年龄。由于Nt=N·e-Mt,Wt=W∞(1-e-k(t-t0)b故B=W∞N0e-Mt(1-e-k(t-t0)b,由dB/dt=0解 得:ta=[1n(b·k+M)-1nM]/k+t0得ta=5.1,即t=5.1时,鲫种群生物量达最大值该年龄又称临界年龄。
2.2.2 资源量
根据费鸿年等人的方法求极限年龄,求得水库鲫的极限年龄tλ=t0+3/k=19.17。
利用FISATⅡ软件的Beverton and Holt plot模块,估算总死亡系数(Z)=0.62。
根据TIOPИH提出的由极限年龄确定死亡率的方法估算自然死亡系数(M),求得自然死亡系数M=(1n1000-1n1)/tλ=0.36。
由于Z为自然死亡系数和捕捞死亡系数F之和,故F=Z-M=0.26。
当前开发率Et=F/Z=0.46。
根据鲫生长参数a、b、k、t0及死亡特征参数L∞、Z、F、M、Et,利用FISATⅡ软件VPA模块估算鲫资源量约33.0万尾,30.08t。
3 讨论
3.1 不同水域鲫生长比较
本研究鲫生长系数(k=0.15)小于长江流域的网湖、黄埔江鲫种群,而渐进体长(L∞)与拐点年龄(tip)大于长江流域湖泊鲫种群,表明其具有较大的生长潜力。与高海拔水域相比,本研究鲫生长系数(k)与额尔齐斯河、博斯腾湖、达里湖、雅鲁藏布江和草海鲫种群相似,这6个水域海拔相对较高,具有相似的水域环境特点,对鲫的生长可能会有一定影响。
本研究鲫生长指数(φ=5.40)与额尔齐斯河、达里湖、雅鲁藏布江和网湖鲫种群相似,略高于博斯腾湖和草海鲫种群,各龄退算体长小于额尔齐斯河、草海和网湖鲫种群,大于博斯腾湖、达里湖和雅鲁藏布江鲫种群。表明,本水库鲫种群总体生长性能较强,这可能与鲫的遗传特性或水体的饵料供给能力有关,有待于进一步研究优于博斯腾湖、达里湖和雅鲁藏布江,而劣于额尔齐斯河、草湖和网湖鲫种群。
3.2 资源管理策略
本研究6.7龄组的鲫生长最快,不过其种群生物量并非最大,这是由于种群数量随年龄增长呈幂函数减少的缘故。故从理论上讲种群生物量最大年龄,即5.1龄起捕是最恰当的。但是,当前水库中鲫的现存量约为30.08t,已超出了水库底栖动物可以提供的渔产潜力(约3.08t/a)。底栖动物虽非鲫唯一的饵料来源,但其较大的种群规模在捕食的过程中的扰底行为会造成水体底质环境的破坏。因此,综合考虑阜康水库鲫的生态与经济效益,建议起捕年龄降至3+,提高开发率控制鲫的种群规模,扩大经济效益。

