利用几何相似性快速测量鱼重的数学模型

杨亚辉

摘 要 本文阐述了在只测量鱼的体长或腰围等参数的情况下，根据鱼的几何相似性快速确定鱼的重量的数学模型。该方法的特点是简单易行，结果也比较准确，在现实生活及生产实际中用途比泛。

【关键词】几何相似性 体长 腰围 鱼 重量 测量 数学模型

1 问题背景

某钓鱼俱乐部计划举办一场钓鱼比赛。出于保护的目的，俱乐部会鼓励会员在钓到鱼后会马上将其放生。同时俱乐部也必须对比赛中会员钓到的鱼的重量进行测量以便进行排名和奖励。如果每人都带一个称，不但携带不方便，而且对特别小的鱼称的并不准确。所以，俱乐部必须找到一种简单快捷的测量鱼的重量的方法。

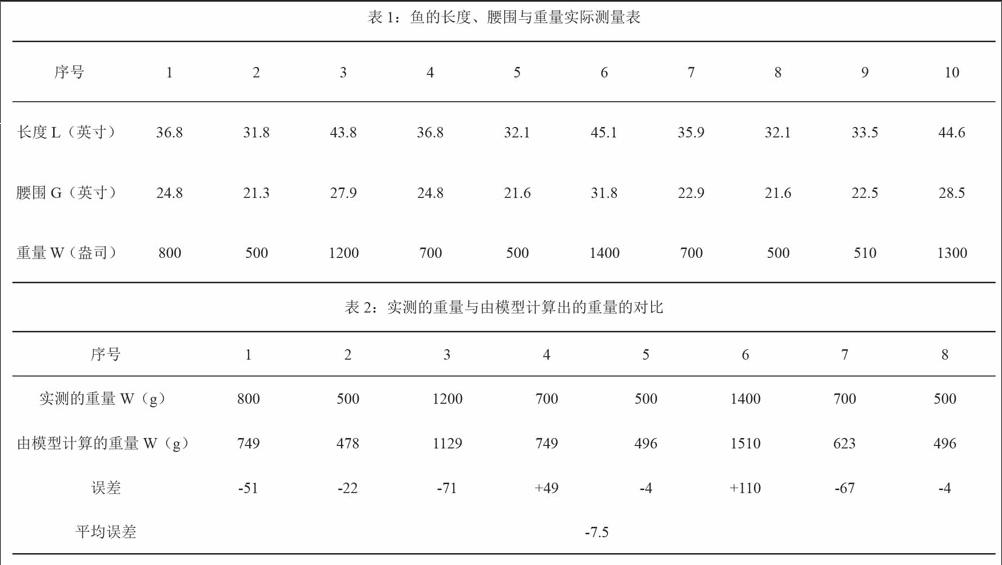
为了获得有用的原始数据，俱乐部提前在钓鱼比赛的水域钓了8条鱼，并将这些鱼的长度L（cm）、腰围G（cm）、重量W（g）的测量值记录在表1。

2 问题分析和假设

鱼的重量与它的体积和密度有关。如果严格按照公式“质量=体积*密度”来建立测量鱼的重量的模型是非常不现实的：

（1）鱼的身体不是一个规则的几何体。

（2）不同种类的鱼及鱼的不同部位的密度也是不一样的。

因此，我们必须对这个问题进行适当的简化。

我们假设：

（1）所有的鱼都是同一种类的，那么鱼的身体之间会呈现出明显的几何相似性。

（2）鱼的密度是一个常数，且不随季节、性别及身边部位的不同而改变。因此体积比较大的鱼就会比较重。于是我们可以不考虑密度的问题，直接建立体积和重量的关系。

（3）鱼的重量的主要部分来自鱼的中部，头部和尾部的占总重量的比重比较小。这一建设可以让我们将鱼想象成一个圆柱，用鱼的体长和腰围来估计鱼的体积。

在这些合理的假设下，问题得到了简化。

3 模型建立与求解

3.1 建立模型

由于前面的分析，我们可以将鱼的体积视为一个圆柱，用鱼的有效长度Long和平均横截面积S分别表示表示这个圆柱的长度和横截面积，则鱼的体积

V= Long×S

由于几何相似性，鱼的有效长度Long和鱼的长度L成正比，鱼的平均横截面积和鱼的腰围G的平方成正比，即

Long∝L

S∝G2

于是，可得

V∝ L×G2

又由于

W∝V

所以

W∝L×G2

引入正比例系数k，得出模型

W=k×L×G2

3.2 求解模型

求出k即可建立由长度和腰围测量重量的模型了。易知，K=W/ （L×G2），为了简化运算，我们就将W，L，G的平均值带入上式求解，用W°，L°，G°分别表示W，L，G的平均值，则

W°=[800+500+1200+700+500+1400+700+500]/8=787

L°=[36.8+31.8+43.8+36.8+32.1+45.1+35.9+21.6]/8=35.4

G°=[24.8+21.3+27.9+24.8+21.6+31.8+22.9+32.1]/8= 25.9

所以

K= W°/ （L°×G°2）=787/（35.4×25.92）=0.0331

则最终的模型为

W=0.0331×L×G2

4 模型的检验

将已知数据L和G代入模型中，可以计算出模型的预测值，并将这个值和实测值进行对比发现模型的准确度较高，平均误差为-7.5g，即按模型估计的值比实际值少了7.5g，这在钓鱼比赛中是完全够用的。如果改进k的求法，模型将更准确。具体结果见表2。

5 模型的应用及推广

由模型W=0.0331×L×G2可以制作一个速查表，只要知道鱼的长度和腰围，便可直接差出鱼的重量，限于篇幅，速查表略。模型W=k×L×G2可广泛用于各种动物体重量的快速测量上。

参考文献

[1]Frank R.Giordano等.数学建模[M].北京：机械工业出版社，2005.

[2]苏金明，王永利.Matlab7.0实用指南[M].北京：电子工业出版，2004.

[3]晓亚，刘平芝等.一种线状要素几何相似性度量方法及其应用[J].武汉大学学报（信息科学版），2015.

[4]安晓亚，孙群，严薇.一种形状多级描述方法及在多尺度空间数据几何相似性度量中的应用[J].测绘学报，2011.

[5]张健，孙满昌.几何相似原理在过滤性渔具网目选择性研究中的应用[J].中国水产科学，2005.

作者单位

海南软件职业技术学院 海南省琼海市 571400