水下无人平台动态布放UUV过程水动力特性

杨壮滔, 张 镇, 何文生, 邵永勇, 赵荣华, 马滇滨

水下无人平台动态布放UUV过程水动力特性

杨壮滔, 张 镇, 何文生, 邵永勇, 赵荣华, 马滇滨

(中国船舶集团有限公司 第705研究所昆明分部, 云南 昆明, 650118)

无人水下航行器; 动态布放; 双体分离; 重叠网格; 多参考系模型; 水动力特性

0 引言

无人水下航行器(unmanned undersea vehicle, UUV)一般由潜艇和水面船只携带抵达作战海域[1]。随着现代科学技术的不断发展, 水下无人作战系统如自航式无人平台以其造价低廉、隐蔽性强、避免人员伤亡、潜伏时间长等诸多优点被越来越多的采用[2-3]。自航式水下无人平台尺寸较潜艇小且能源有限, 多采用UUV自航布放方式[4], 而UUV自航发射分离阶段航速慢, 在无人平台动态布放时易受平台航行的干扰, 甚至使UUV在分离阶段失控, 因此亟需对水下无人平台动态布放UUV过程水动力特性开展研究。

目前计算流体动力学(computational fluid dy- namics, CFD)仿真是单体UUV水动力参数预报方法之一, 但针对基于CFD的双体分离水动力参数预报方法研究较少, 且使用模型试验难以实现。对于双体分离的研究, 多使用动网格方法, 如: Huang等[5]使用数值方法研究动态分离; 李湘平等[6]使用动网格法研究了弹托分离; 杨磊[7]使用动网格法研究了航天器空中分离。然而, 使用动网格法对分离过程仿真仅能得到单一固定姿态所受的流体力和弹道信息, 无法直接提取UUV的各项水动力参数。文中基于CFD方法, 使用重叠网格并结合多参考系(multi-reference frame, MRF)模型, 建立了一种适用于研究动态布放与双体分离的数值水池, 对水下无人平台动态布放UUV过程水动力特性开展研究, 可为UUV布放过程与控制策略设计提供参考。

1 建模与仿真

1.1 计算方程

对于不可压非定常粘性流体, 雷诺平均法(Reynolds average Navier-Stockes, RANS)是工程上常用的CFD方法之一。其中, 空间离散采用有限体积法, 时间推进采用双时间法。该方法的连续性方程和动量方程可写为

1.2 MRF模型

在实际布放与分离过程中, 自航式无人平台与UUV之间存在相对运动, 二者的相对位置随时间变化, 自航式平台对UUV的干扰也随时间变化, 理论上是一个非定常问题。对此非定常问题进行简化, 取二者分离过程中某一时刻作为研究对象, 将任一时刻的非定常流场假设为定常进行计算, 近似于获得流动的“快照(snapshot)”[9]解, MRF模型正是基于这种方法。目前, MRF多用于旋转机械仿真领域, 虽然无法得到流体动力参数时历值, 但能够得到流体动力参数平均值, 更利于流体动力无量纲导数工程化求解[10-11]。

MRF模型将计算域划分为不同子域, 并在子域内建立与背景域不同的参考系。针对动态布放与双体分离问题, 在计算域中划分一个子域将其中一个分离模型完全包络, 如图1所示, 并在该子域中建立与分离模型运动完全一致的坐标系, 即可将相对运动转化为静态计算。另一个分离体位于背景域内, 两域之间交接用交界面连接, 用于数据传递。

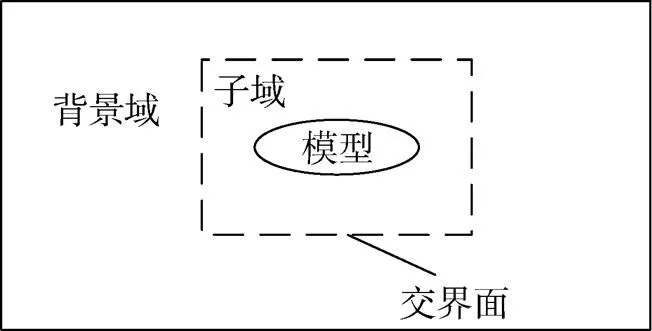
图1 多域示意图

将整个计算域划分为背景域和子域2个计算域, 其中自航式平台位于背景域中, 其外围边界为速度入口和压力出口; UUV位于子域中。设置子域网格为重叠网格, 如图2所示, 计算时UUV所在重叠网格与自航式平台所在背景网格进行数据传递和数值差分。在UUV子域建立运动坐标系, 在此坐标系中, 网格在计算时保持静止, 即可将自航式平台和UUV的相对运动转化为静态计算。考虑了求解旋转力时的哥氏力和离心力后进行定常计算[12]。

图2 计算网格

运动坐标系下的动量方程为

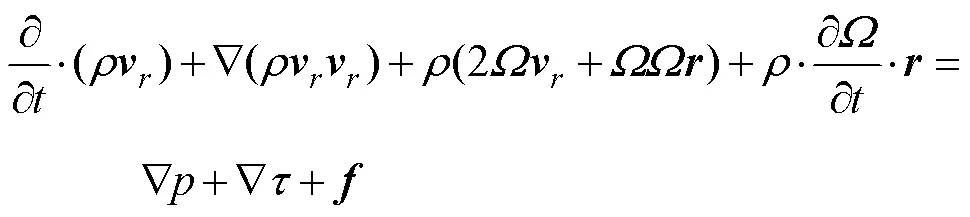
通过上述理论, 建立一种适用于研究自航式平台动态布放UUV的数值水池, 以求解分离过程中任意时刻UUV的水动力参数。

2 典型算例验证

选用某型单体UUV作为典型模型, 使用文中建立的仿真方法求解该模型水动力参数, 并与其模型试验数据进行对比, 以验证其求解精度。

2.1 计算域及边界处理

2.2 计算结果与试验对比

对典型模型无动力状态下的位置力、旋转力和舵力开展仿真计算, 并求解相关无量纲导数。仿真模型长为4 m, 计算域长、宽和高分别为20 m、4 m和4 m, 网格数量为890万, 最小网格尺度为1 mm。在计算时对典型模型所受流体动力和对浮心力矩进行监测。试验模型与计算模型同尺寸, 通过风洞试验测量模型位置力和舵力, 通过悬臂水池试验求解模型旋转力, 并求解相关无量纲导数。

图3 典型算例验证压力分布

2.2.1 位置力

求解位置力, 分别计算模型航速为6 m/s且纵倾角=2º～10º时所受升力和升力对浮心产生力矩M, 通过数据处理, 得出相应的升力系数C和力矩系数m。不同纵倾角下典型模型的升力系数C和力矩系数m的对比如图4和图5所示。

图4 位置力系数仿真与试验结果对比

图5 位置力矩系数仿真与试验结果对比

仿真与试验结果较为接近。具体计算误差见表1, 不同纵倾角下2项系数计算误差均小于8%。

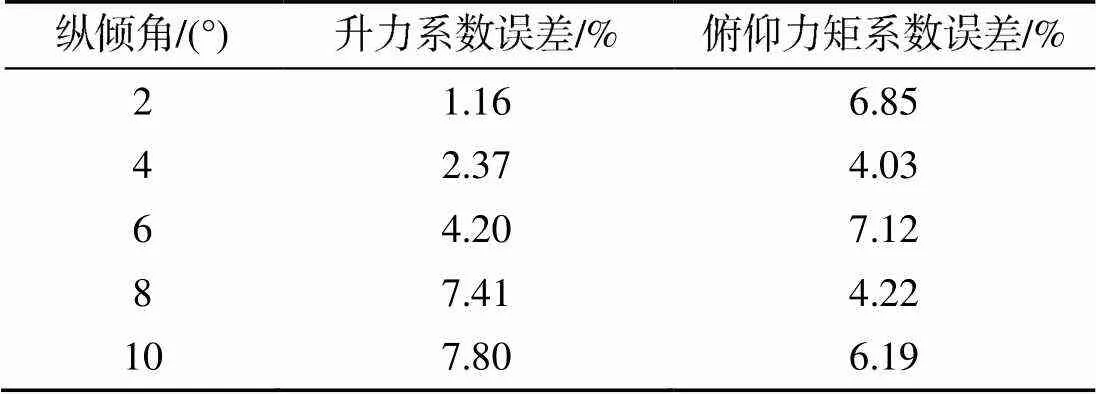
表1 位置力系数与力矩系数误差仿真结果

2.2.2 旋转力

求解旋转力, 设置典型模型绕轴旋转, 分别计算旋转力F和旋转力对浮心的力矩M, 速度系数对应的角速度和回转半径如表2所示。经计算不同角速度系数下典型模型受到旋转力系数C和旋转力矩系数m对比如图6和图7所示。

表2 角速度系数相关参数

图6 旋转力系数仿真与试验结果对比

图7 旋转力矩系数仿真与试验结果对比

仿真与试验结果较为接近, 具体计算误差如表3所示, 不同角速度系数(角速度与回转半径相关)下2项系数计算误差均小于6%。

表3 旋转力系数与力矩系数误差仿真结果

2.2.3 操舵力矩

图8 操舵力矩系数仿真与试验结果对比

仿真与试验结果较为接近, 具体计算误差如表4所示, 不同舵角下操舵力矩系数计算误差均小于6%。

表4 操舵力矩系数误差仿真结果

3 工程实例

使用文中建立的数值水池求解UUV分离时水动力参数, 与自由状态水动力参数进行对比, 定性分析平台对UUV的干扰形式, 并定量分析受干扰程度, 为分离过程设计和控制策略设计提供指导。

3.1 计算域及边界处理

为动态仿真布放分离, 使用所建立的数值水池, 自航式水下无人平台位于背景域中, 假设布放时平台只作向前匀速直线运动, 设置自航式平台航速边界条件仅需通过背景域速度边界设置。平台布放的UUV位于建立了运动坐标系的子域内, 通过在运动坐标输入相对背景域坐标的相对速度赋予布放UUV的速度边界。计算网格如图9所示。

图9 工程实例计算网格

3.2 布放分离与自由状态对比分析

在上述工况下, 针对UUV布放分离时位置力、旋转力和舵力开展仿真计算, 在计算时对UUV模型所受流体动力和浮心力矩进行监测, 当连续性残差曲线趋于稳定且小于1×104, 监视力、力矩趋于稳定且波动小于1%时, 判定计算收敛, 取满足条件的力和力矩的平均值作为数值计算结果。布放状态压力分布如图10所示, 自由状态压力分布如图11所示。

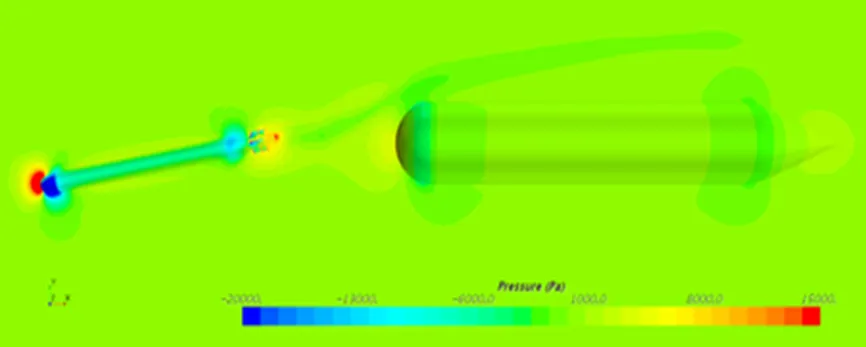
图10 布放状态压力分布

图11 自由状态压力分布

3.2.1 位置力

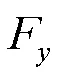
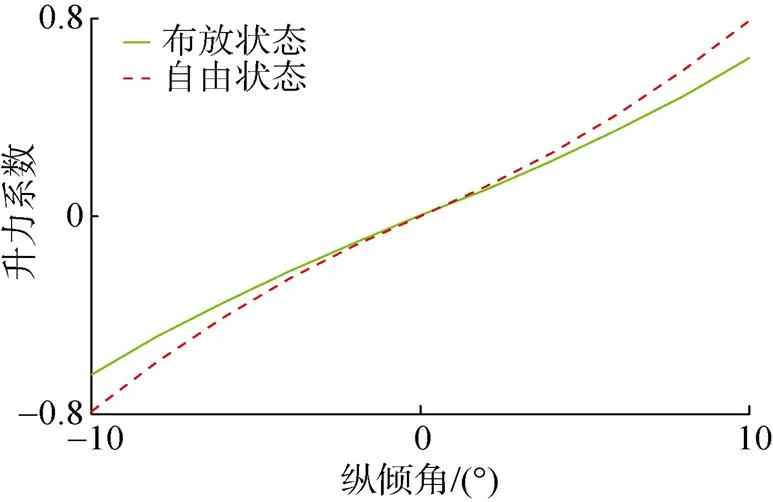
图12 布放与自由状态下位置力系数曲线

图13 布放与自由状态下位置力矩系数曲线

布放分离时UUV升力系数C绝对值大小和俯仰力矩系数m绝对值大小均小于自由状态, 具体误差如表5所示。

3.2.2 旋转力

求解旋转力, 设置典型模型绕轴旋转, 分别计算旋转力和旋转力对浮心的力矩, 速度系数对应的角速度和回转半径见表6。经计算, 不同角速度系数下典型模型受到旋转力系数和旋转力矩系数对比分别如图14和图15所示。

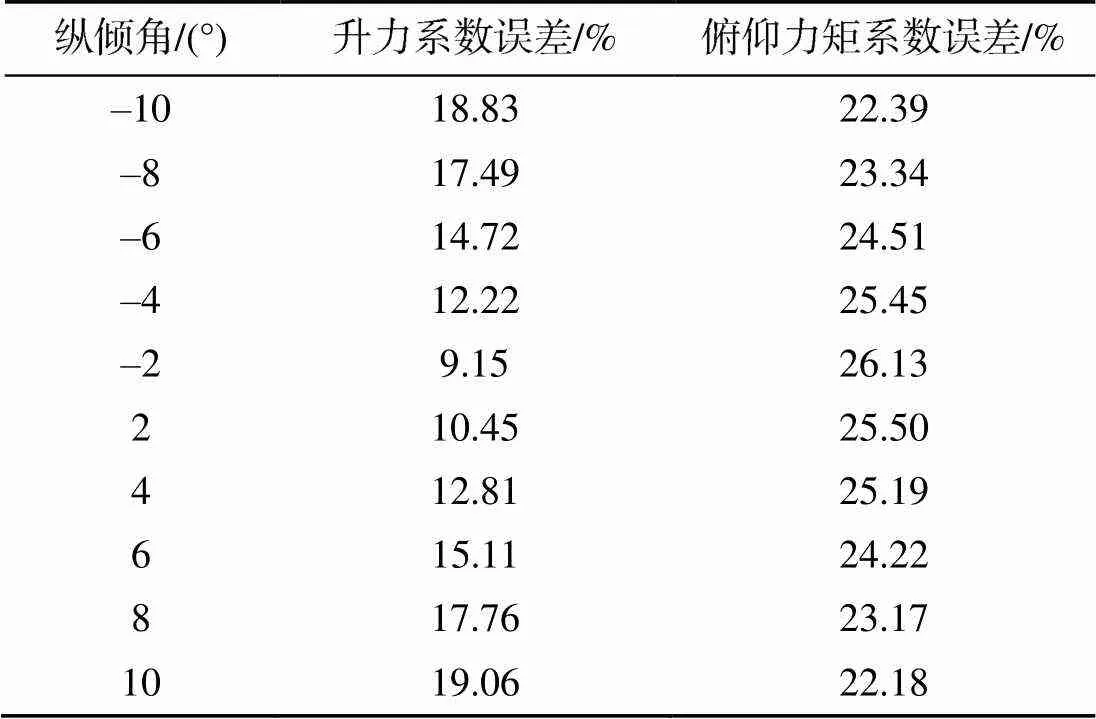
表5 布放与自由状态位置力系数与力矩系数误差

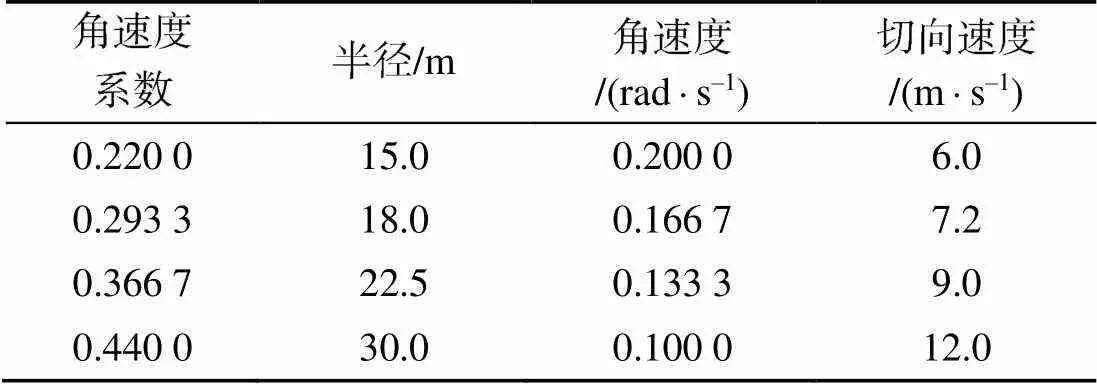
表6 角速度系数相关参数

图14 布放与自由状态下旋转力系数曲线

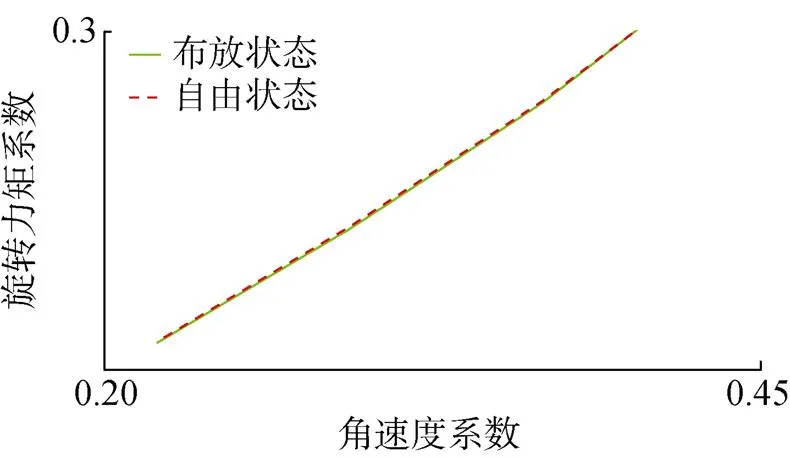
图15 布放与自由状态下旋转力矩系数曲线

布放分离时UUV旋转力系数C大于自由状态, 俯仰力矩系数m与自由状态相差较小, 如表7所示。

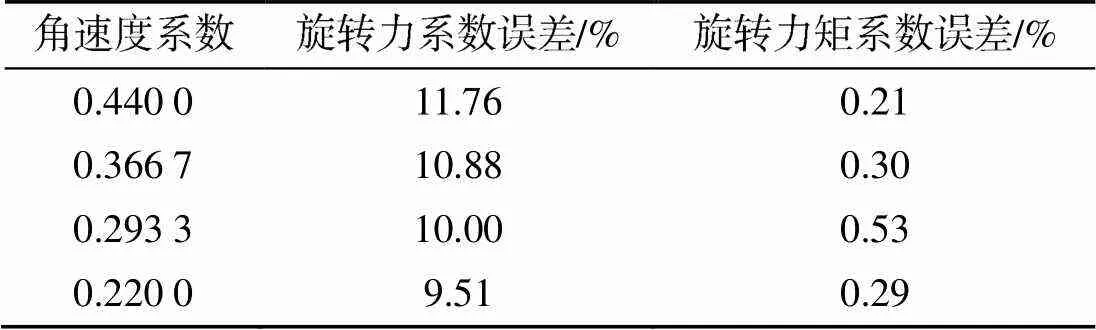
表7 布放与自由状态旋转力系数与力矩系数误差

3.2.3 操舵力矩

求解操舵力矩, 分别设置UUV执行水平舵操舵指令, 计算操舵舵角为–20°～20°时水平舵受到力和水平舵对浮心产生的操舵力矩。通过数据处理, 得出相应的操舵力矩系数对比, 如图16所示。

图16 布放与自由状态下操舵力矩系数曲线

布放分离时, UUV操舵力矩系数与自由状态相差较小, 如表8所示。

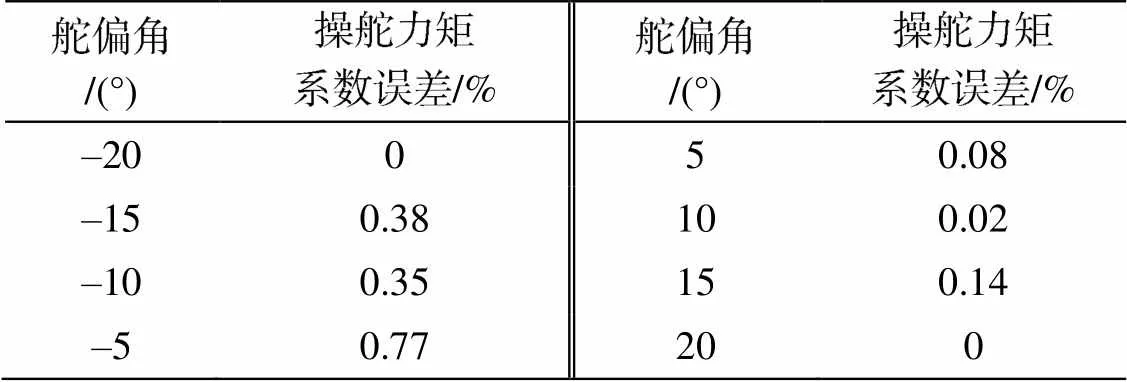
表8 布放与自由状态操舵力矩系数误差

4 结论

文中研究可为自航式载体动态布放UUV的过程设计和控制策略设计提供参考。

[1] 陈强, 孙嵘.潜艇布放回收UUV方式[J].舰船科学技术, 2011, 33(7): 145-149.

Chen Qiang, Sun Rong.Analysis of Launch and Recovery UUV Model for Submarine[J].Ship Science and Techn ology, 2011, 33(7): 145-149.

[2] 李经.水下无人作战系统装备现状及发展趋势[J].舰船科学技术, 2017, 39(1): 1-5, 36.

Li Jing.Existence and Development Trend of Navy Autonomous Underwater Combat System[J].Ship Science and Technology, 2017, 39(1): 1-5, 36.

[3] 杨智栋, 李荣融, 蔡卫军, 等.国外水下预置武器发展及关键技术[J].水下无人系统学报, 2018, 26(6): 521-526.

Yang Zhi-dong, Li Rong-rong, Cai Wei-jun, et al.Deve- lopment and Key Technologies of Preset Undersea Weapon: a Review[J].Journal of Unmanned Undersea Systems, 2018, 26(6): 521-526.

[4] 杨文, 马亮.UUV自航发射方法探究[J].舰船科学技术, 2017, 39(12): 114-117.

Yang Wen, Ma Liang.Research on Technology of Self- prorelled Launching UUV[J].Ship Science and Tech- nology, 2017, 39(12): 114-117.

[5] Huang Z G, Wessam M E, Chen Z H．Numerical Investi- gation of the Three-dimensional Dynamic Process of Sabot Discard[J]．Journal of Mechanical Science and Technology, 2014, 28(7): 2637-2649.

[6] 李湘平, 鲁军勇, 冯军红, 等.采用动网格技术的弹托分离仿真模型[J].国防科技大学学报, 2018, 40(5): 9-13.

Li Xiang-ping, Lu Jun-yong, Feng Jun-hong, et al.Simulation Model for Sabot Discard Using Dynamic Mesh Technique[J].Journal of National University of Defense Technology, 2018, 40(5): 9-13.

[7] 杨磊.空中发射分离过程的动力学问题研究[D].西安: 西北工业大学, 2018

[8] 马峥, 黄少锋, 朱德祥.湍流模型在船舶计算流体力学中的适用性研究[J].水动力学研究与进展, 2009, 24(2): 207-216.

Ma Zheng, Huang Shao-feng, Zhu De-xiang.Study on Applicability of Turbulence Model in Ship Computational Fluid Dynamics[J].Chinese Journal of Hydrodynamics, 2009, 24(2): 207-216.

[9] Deglon D A, Meyer C J.CFD Modeling of Stirred Tanks Numerical Considerations[J].Minerals Engineering, 2006, 19(10): 1059-1068.

[10] 陈志明, 袁剑平, 严谨, 等.基于MRF方法和滑移网格的螺旋桨水动力性能研究[J].船舶工程, 2020, 42(z1): 157-162, 311.

Chen Zhi-ming, Yuan Jian-ping, Yan Jin, et al.Study on Hydrodynamic Performance of Propeller Based on MRF Model and Sliding Mesh[J].Ship Engineering, 2020, 42(z1): 157-162, 311.

[11] 王艳冰, 项松, 苏亚楠, 等.孤立两叶螺旋桨风洞试验准定常数值模拟[J].应用力学学报, 2020, 37(3): 1196-1201.

Wang Yan-bing, Xiang Song, Su Ya-nan, et al.Numerical Simulation of Isolated Two-blade Propeller Wind Tunnel Test[J].Chinese Journal of Applied Mechanics, 2020, 37(3): 1196-1201.

[12] 张涛, 杨晨俊, 宋保维.基于MRF模型的对转桨敞水性能数值模拟方法探讨[J].船舶力学, 2010, 14(8): 847-853.

Zhang Tao, Yang Chen-jun, Song Bao-wei.Investigations on the Numerical Simulation Method for the Open-water Performance of Contrarotating Propellers Based on the MRF Model[J].Journal of Ship Mechnics, 2010, 14(8): 847-853.

Hydrodynamic Characteristics of UUV during Dynamic Deployment Process of Underwater Unmanned Platform

YANG Zhuang-tao, ZHANG Zhen, HE Wen-sheng, SHAO Yong-yong, ZHAO Rong-hua, MA Dian-bin

(Kunming Branch of the 705 Research Institute, China State Shipbuilding Corporation Limited, Kunming 650118, China)

unmanned undersea vehicle(UUV); dynamic deployment; catamaran separation; overlapping grid; multi-reference frame(MRF); hydrodynamic characteristic

杨壮滔, 张镇, 何文生, 等.水下无人平台动态布放UUV过程水动力特性[J].水下无人系统学报, 2022, 30(1): 115-121.

TJ630; TB71.2

A

2096-3920(2022)01-0115-07

10.11993/j.issn.2096-3920.2022.01.015

2016-11-19;

2016-12-18.

杨壮滔(1993-), 男, 硕士, 工程师, 主要研究方向为水中兵器总体设计

(责任编辑: 杨力军)